TL;DR: gpt2-small's head L1H5 directs attention to semantically similar tokens and actively suppresses self-attention. The head computes attention purely based on token identity, independent of position. This mechanism is driven by a symmetric bilinear form with negative eigenvalues, which enables suppression. We cluster tokens semantically, interpret the weights to explain the attention scores, and steer self-suppression by tuning eigenvalues.
work performed as part of ARENA 5.0 Capstone project.
Within gpt2-small lies an unusual component: attention head L1H5[1] which fires on semantically similar concepts. It excels at connecting related concepts: the token cat attends to dog, and red attends to green and blue. Normally, this would be unsurprising, as we would expect embedding vectors to already cluster based on topic/semantic categories. But oddly enough, for this head, tokens do not attend to themselves. For example, the token dog will attend to other animals in the context, but it will not attend to itself or other instances of the token dog.
This behaviour is too specific to be an accident. This short research project aims to find the mechanistic explanation for this semantic grouping and self-avoidance, with the goal to develop useful techniques for analyzing attention patterns along the way.
The Behaviour: Three Simple Rules
Before diving into the mechanistic analysis, let's establish exactly what GPT-2 head L1H5 is doing. After analyzing its attention patterns across hundreds of sequences, the behaviour can be summarized by three rules:
- Semantic Clustering: A token attends to other tokens in the sequence that belong to the same semantic category. Examples:
catattends todogandhorse, (animals)redattends toblue,greenandyellow. (colours)Mondayattends toTuesdayandFriday. (days of the week).
- Self-Suppression: A token does not attend to itself, even when it appears multiple times in the sequence.
- Fallback to Beginning: If no other token in the sequence belongs to the same semantic category, the token attends to the
<bos>(beginning of sequence) token.
These rules hold remarkably consistently across different types of semantic categories, colours, months, days of the week, numbers, names, even verbs and logical operators. Broadly, the behaviour of this head as a semantic head was already mentioned in We Inspected Every Head In GPT-2 Small using SAEs So You Don’t Have To, but there it's only described as a "Succession or pairs related behavior".
Part 1: Finding What Matters
First, we need to isolate this behaviour and find the components responsible for it. This required a three-step process: design a prompt to reliably trigger the behaviour, define a metric to measure it, and ablate components to see which ones break it.
Setup
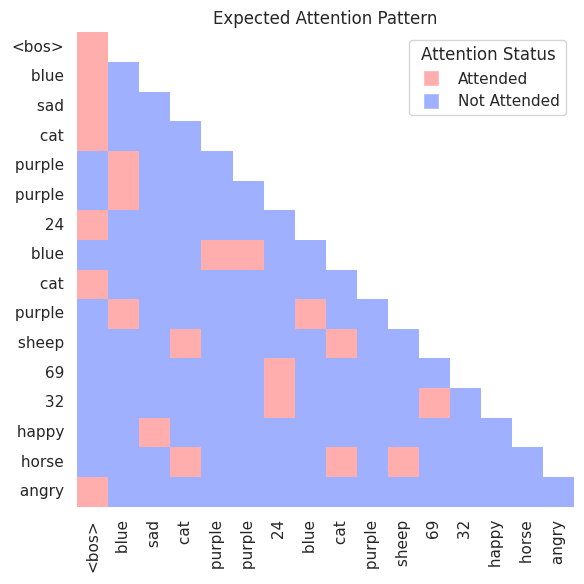
To reliably trigger the head's behaviour, we define a simple prompt by shuffling tokens from various hand-picked semantic categories. This creates a context where L1H5 has many opportunities to demonstrate its preference for in-category attention.
<bos> blue sad cat purple purple 24 blue cat purple sheep 69 32 happy horse angryBased on the three rules observed above, we define an "expected" attention pattern for this prompt. For example, purple should attend to blue, but not to cat or purple. This gives us a target mask representing the idealized behaviour of the head.
Semantic Category Score
To measure how well the head's actual attention pattern, , matches the expected pattern, , we use a KL divergence-based score: where is the probability mass of concentrated in . The goal here is to measure how much of the attention probability mass is concentrated where the mask says it should be. This leads to the following loss function (credit to @David Quarel for the derivation):
A lower score means a better match. As expected, a survey of all heads in the model shows that L1H5 is an outlier with a uniquely low score, confirming it's specialized for this task.
Loss derivation
We define this metric as the distance from the expected behaviour described above. We encode the expected behaviour through the mask matrix , and define as the amount of probability mass that the attention scores places on other tokens in the same semantic category. We can then measure the distance of as the KL divergence from the ideal distribution where all the probability mass is concentrated where we expect it to be. Then this derivation follows
A KL divergence between and devolves in . This is also called Shannon Information. We then take the average across all queries .
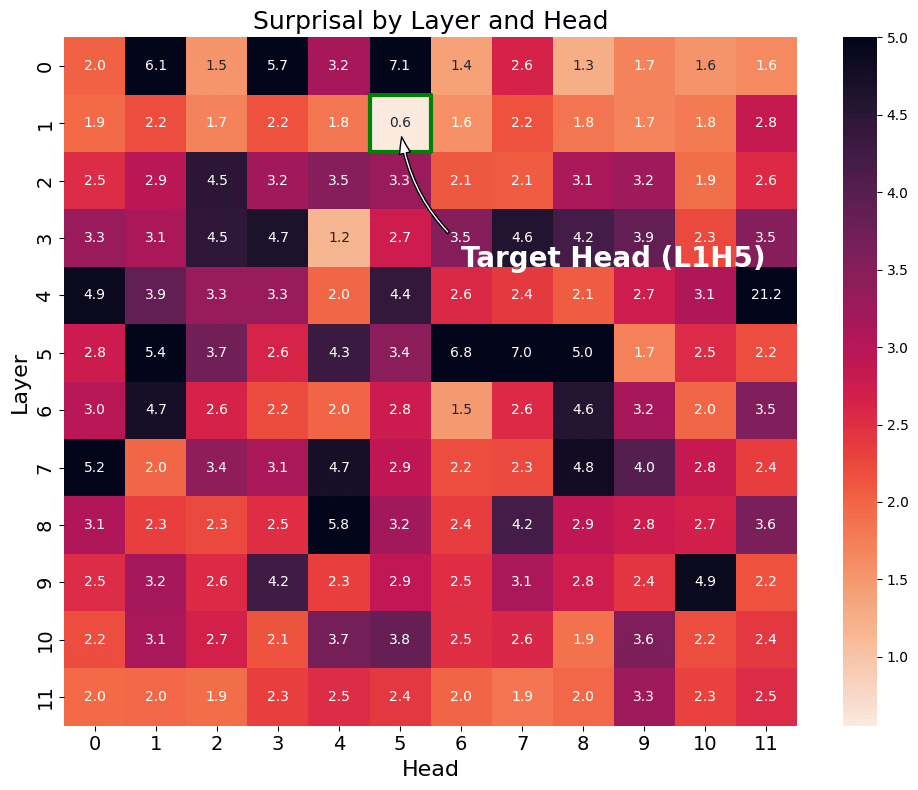
Component Importance
With a reliable metric, we can perform a mean-ablation study[2]. We systematically replace the output of each preceding component with its mean value and check whether the Semantic Category Score increases; if it does it means that the component is relevant for L1H5.
Surprisingly, 2 out of 4 components are completely irrelevant. The head's behaviour appears to be affected only by:
- The token embedding matrix, .
- The first MLP layer, .
- The residual stream around the first MLP.
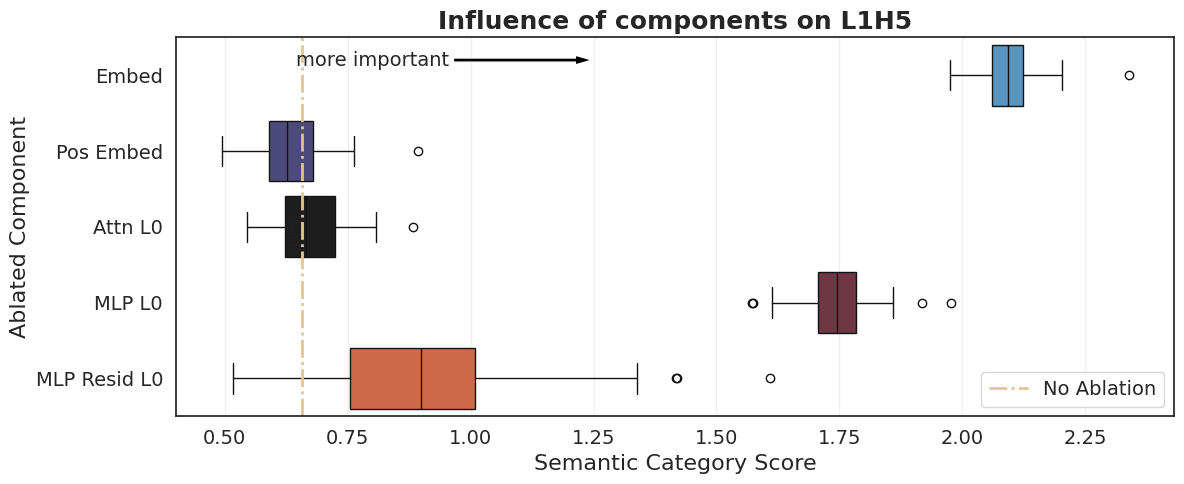
Interestingly, ablating the positional embeddings () and the previous attention layer () had almost no effect. This is a crucial clue: L1H5 isn't using positional or sequential information to avoid attending to itself. The self-suppression mechanism must be inherent to the token representations themselves, which in turn depend only on the embedding matrix () and the MLP.
From this, we conclude that the essential input to L1H5 can be represented simply as:
This matrix E contains a "processed" embedding for every token in the vocabulary, and it's all L1H5 needs to perform its function.
Part 2: The World According to L1H5
With the key inputs isolated, we now map the head's behaviour across the entire vocabulary. We will compute a full token-to-token attention matrix and use clustering algorithms to chart the head's internal 'world model'.
First, since the input is all we care about, we can circumvent the rest of the network and compute a full token-to-token attention score matrix directly:
Here, is the attention head's QK circuit. Visualizing this for selected semantic groups reveals the behaviour perfectly: high scores within a semantic block (e.g., colours attending to other colours) but low scores on the diagonal (a token attending to itself).
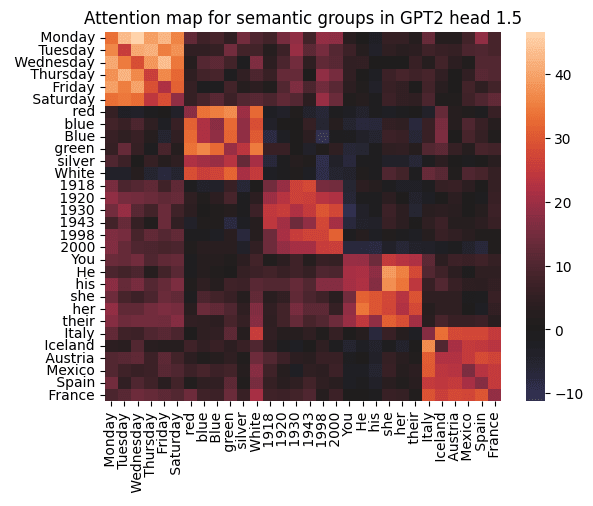
The head's semantic groupings are robust and intuitive, here we show the top 10 attended tokens for a sample of input tokens:
| Input Token | Top Attended Tokens |
|---|---|
red | Green, Blue, green, blue, _green, Yellow, GREEN, _blue, Green, White |
69 | 72, 82, 70, 62, 71, 80, 68, 67, 66, 78 |
Monday | Wednesday, Tuesday, _Wednesday, _Tuesday, Friday, Tonight, _Friday, tonight, Tonight, tomorrow |
Italy | Iceland, Turkish, Pakistani, Auckland, Portugal, Guatemala, Zealand, Pakistan, Mexican, Chile |
Again note that red doesn't attend to red, nor to same meaning tokens like _red, RED, _Red, etc...
Clustering
Using this attention map, we ran the Leiden community detection algorithm[3] to cluster the main 3000 tokens of English language. The resulting clusters are surprisingly coherent and offer a fascinating glimpse into the "world model" of this specific head. You can explore this interactive map for yourself here[4].
If you do you may note some interesting clusters:
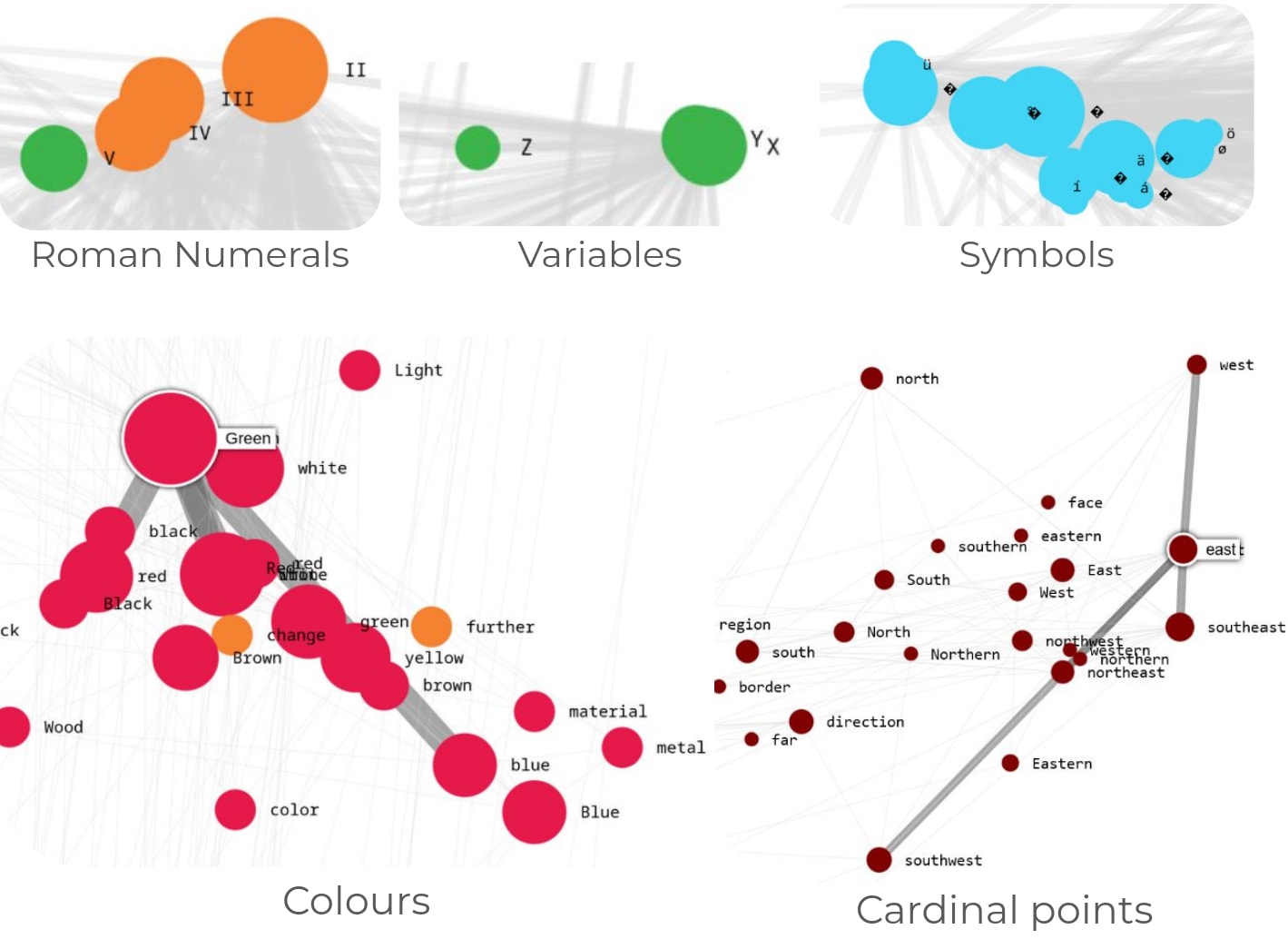
east doesn't attend to East, Eastern, eastern.
Part 3: The Mechanism of Self-Suppression
To find the mechanism, we look inside the attention calculation itself. We will decompose L1H5's matrix to find the mathematical property that drives both semantic grouping and self-suppression.
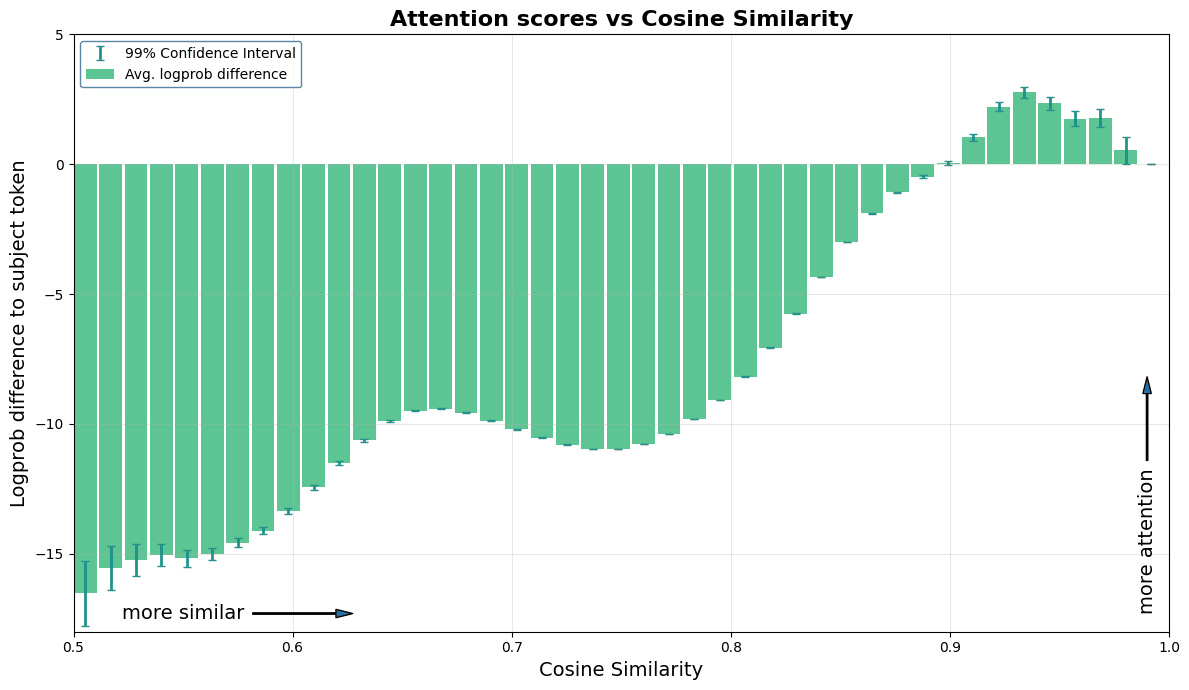
How does a single matrix, , implement this complex behaviour? Formally, for a query vector , a similar vector (high cosine similarity), and a dissimilar vector , we want:
To empirically verify this we can plot the average attention score obtained by a pair in L1H5 against their initial similarity. We can notice that the peak attention score is not at a similarity of 1, but below it, at circa 0.95, showing the head prefers tokens that are similar, but not identical.
Decomposing the Matrix
To understand how works, we start by decomposing it into its symmetric and skew-symmetric parts:
This decomposition is useful because the skew-symmetric part always has zero contribution to self-attention .
When we test these components separately, the result is clear. The symmetric matrix, , is able to reproduce the full behaviour on its own: high off-diagonal attention within semantic blocks and low diagonal self-attention. The skew-symmetric part has a negligible effect.
About
We note that the norm of attention scores produced by is significantly lower than the , and its maximum singular value is comparatively lower than the then (1.3473 vs. 1.8611), indicating a smaller overall contribution to the final logits.
While might be involved in encoding ordering or sequence information, these observations suggest that its precise role in the self-suppression mechanism is minor, prompting us to primarily focus on for further investigation.
The Role of Eigenvalues
So, the mystery is contained entirely within , how does it suppress self-attention? Let's start by decomposing in its eigenvalues () and eigenvectors (), such that . For any symmetric matrix these values are going to be real. The attention score is then:
If all eigenvalues were positive, this score would always be positive. A vector would achieve its highest score by aligning with the eigenvectors corresponding to the largest positive eigenvalues.
This leads to our central hypothesis: self-suppression occurs when has negative eigenvalues. If a vector has a significant projection onto an eigenvector whose eigenvalue is negative, that component will be negative, reducing the total score.
The head suppresses self-attention for a vector by having it align with "suppressive directions" in the space defined by .
Part 4: Validation by Steering
To explore the proposed link between structure and function, we will perform a direct intervention by modifying the head's core matrix, attempting to 'steer' self-suppression and test the link between structure and function.
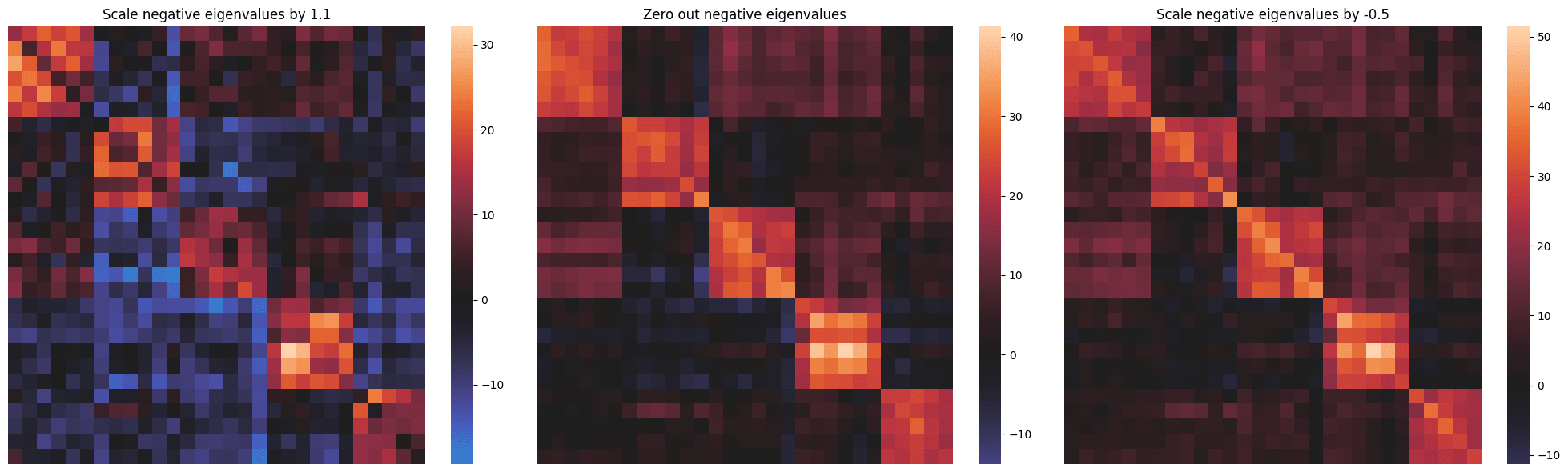
Specifically, we compute the 64 eigenvalues of and find that 33 are negative, suggesting a structural basis for the behaviour. To test this, we define a steering mechanism that scales all negative eigenvalues by a factor , allowing us to elicit or remove the behaviour in a controlled way.
# Decompose the symmetric matrix
eigenvalues, eigenvectors = eigen_decomposition(W_sym)
# Scale the negative eigenvalues
for i in range(len(eigenvalues)):
if eigenvalues[i] < 0:
eigenvalues[i] *= alpha
# Reconstruct the steered matrix
W_steered = eigenvectors * diag(eigenvalues) * eigenvectors.T
# Compute new attention map
attn_map = E * W_steered * E.TWe scale negative eigenvalues by a parameter , reconstruct , and recompute attention.
- reduces self-suppression (self-attends more)
- strengthens self-suppression.
This gives direct causal control over whether tokens attend to themselves while preserving semantic clustering. As it can be seen by the plot below, when scaling we can successfully steer the attention map, while also maintaining the similarity of semantically related tokens.
Conclusion
This study offers a mechanistic account of gpt2-small attention head L1H5’s unusual behaviour. Its tendency to attend to semantically related tokens, while suppressing self-attention, appears to arise from a symmetric bilinear form with carefully placed negative eigenvalues. This effect seems to operate independently of position, relying only on transformed token embeddings. Decomposing the attention matrix and inspecting its spectrum suggests that negative eigenvalues play a key role in self-suppression. Moreover, this behaviour can be steered by adjusting the spectrum, pointing to a possible causal link between spectral structure and function. These results add to our grasp of attention in LLMs and hopefully hint at new ways to interpret and steer their internal workings.
My appreciation goes to David Quarel, Indro Spinelli, Michele Mignani, Lorenzo Venieri, and Simone Facchiano, whose insights and review greatly improved this article. I'm also grateful to ARENA 5.0 for creating an environment that encourages exploration and growth.




