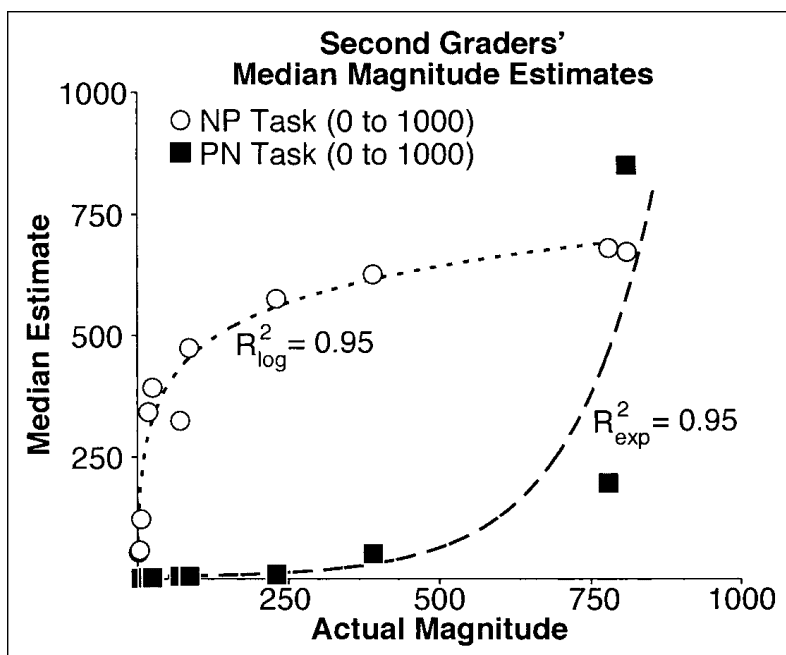
This paper says:

it was shown that second-grade children unevenly placed numbers on a 0–1000 number line as their placement pattern was best fit by a logarithmic rather than by a linear function. The same age group placed numbers more linearly (i.e., resulting in a constant distance between consecutive numbers) on a 0–100 number line. In contrast, adults produced a linear distribution when placing numbers on a 0–1000 number line

Two developmental leaps occurring during elementary school were recognized: (1) the division of the number line into two segments and (2) consistent use of different anchor points on the number line—the left endpoint in first grade, the right endpoint in second grade, and finally the midpoint in third grade.

People mentally represent numbers as positions on a number line. I consider this a latent space representation. Human conceptual capabilities imply ability to at least average latent space representations, and possibly add them, which could then be used for fast approximation of sums. If only averaging is possible, then a 2-step (average -> double) process would be needed. The accuracy of that approach is insufficient for solving arithmetic problems, so people often instead use a much slower algorithm with exact accuracy.

Per the linked paper, 2nd-grade children have a tendency to place large numbers logarithmically, which implies to me an approximately logarithmic latent space representation. In that case, an accurate logarithmic representation should also be something humans are capable of with some training. In an accurate logarithmic representation, addition and subtraction are, of course, equivalent to multiplication and division.

Is it possible for people to do fast mental multiplications with the accuracy of a typical slide rule, by learning a logarithmic mental representation of numbers between 1 and 10? It seems plausible to me. Any big mental arithmetic fans around here?

But of course, the latent spaces humans typically use are high-dimensional, with limited range in any given dimension. It's possible that the "linear" number line in human mental representations is curved in its latent space to better utilize high dimensionality. In that case, averaging representations of distant numbers doesn't work so well.

Supposing that the mental number line is curved, how is it linearized when people write numbers on a line? My guess would be that it involves finding distances between the number embedding and the embeddings of nearby anchor points (like 1/2, 3/4, etc).

Some curled number lines would allow for better averaging of representations than others. Supposing that children learning arithmetic learn such curled line structures on their own, it could be more efficient to directly train them on multidimensional lower-precision representations of numbers that work relatively well for averaging/adding/doubling.