A few weeks ago, Thomas Philippon released a paper in which he argued that total factor productivity growth was piecewise linear rather than exponential. The paper received attention both on social media and on LessWrong itself.

I'll use this paper to illustrate a problem that I think is widespread, so while part of what I will say is a criticism of this specific paper the point I'm trying to make is more general.

What is TFP?

First, some background: total factor productivity (TFP) is often (wrongly, in my view) used as a proxy of technology in growth economics. Technically, it's the residual estimate of a log-linear regression of GDP on some quantifiable variables, such as the labor and capital stock of a country. The idea is to assume that there is a relationship $Y=A{L}^{1-\alpha }{K}^{\alpha }$ between the GDP $Y$, labor stock $L$ and capital stock $K$ of countries for some $\alpha$, estimate $\alpha$ from a linear regression

$$\log \left(Y\right)=c+\alpha \log \left(K\right)+(1-\alpha )\log \left(L\right)+\epsilon$$

and then use the measured $\alpha$ to back out estimates for $A$ across countries and across time. $A$ is then the "total factor productivity" - it's the part of GDP that's unexplained by how many people are working and how much capital equipment they have at their disposal.

The GDP of an individual country can therefore increase for three reasons: it has more total hours worked, more capital equipment or more total factor productivity. Notice that this statement is vacuously true and is a tautological consequence of the definition of total factor productivity.

It's a robust fact that TFP as defined above increases in most countries over time. What this means is that not only do countries expand their labor force and acquire more capital thanks to investment, they also become "more efficient" at using those inputs in some sense. For instance, if our definition of TFP is relative to labor and capital stocks, it might fail to capture that workers are also becoming more skilled. Economists usually call this "human capital" and we can try to include it in a regression, but since TFP is defined to be all the stuff we left out of the regression, if we only work with $L$ and $K$ then workers becoming more skilled will show up in our data as an increase in $A$.

The question that's the subject of Philippon's paper is about the growth process of $A$. Economists usually model TFP as an exponentially growing process, say, $\log \left(A_{t+1}\right)=\log \left(A_t\right)+\mu +{\epsilon }_t$ where $\mu$ is an average growth rate and $\epsilon$ is white noise. Philippon investigates the alternative hypothesis that the growth is linear: we have $A_{t+1}=A_t+\mu +{\epsilon }_t$.

I've already criticized some of the paper's methodology in a comment, so I won't repeat what I've said here. What I will say is that there's a major shortcoming of Philippon's paper even if he's completely right and all of his analysis is sound: he doesn't report likelihood ratios. (In fact he doesn't report likelihoods at all, but we'll get to that later.) He reports a bunch of other statistics which appear to support the linear model over the exponential one, but no likelihood ratios.

Why care about likelihoods?

Why is this such a problem? Why aren't Philippon's root mean squared error estimates as good as reporting likelihoods?

The reason is that likelihoods are what a Bayesian cares about. If you read Philippon's paper and see that the data seems to favor the linear model over the exponential one, setting aside concerns about whether the analysis was properly done, there is an added concern over how much you should update from your prior beliefs based on the arguments in the paper. If the linear model fits the data better, you might ask "how much better", and the relevant quantity you care about at parameter parity is what likelihood the linear model assigns to some data compared to the exponential model.

If the linear model assigns the data 100 times the probability that the exponential model assigns it, you should multiply the ratio of your priors for the two classes of models by a factor of 100 in favor of the linear model. This is just a restatement of Bayes' rule. We can see this by just computing:

$$\frac{P\left(L\right|D)}{P\left(E\right|D)}=\frac{P\left(D\right|L\left)P\right(L)}{P\left(D\right|E\left)P\right(E)}=\frac{P\left(D\right|L)}{P\left(D\right|E)}\times \frac{P\left(L\right)}{P\left(E\right)}$$

Here $L$ denotes "the right model is linear", $E$ denotes "the right model is exponential", and $D$ stands in for the data we've observed.

Without the likelihood ratio $P\left(D\right|L\left)/P\right(D\left|E\right)$, we don't know how convincing the results in the paper are and how strong the evidence they provide for $L$ over $E$ is. Of course there are ways to hack likelihoods just like any other test statistic, but the fact that the paper doesn't even bother reporting likelihoods at all is a more serious problem.

Computing likelihoods

Since the paper doesn't report likelihoods, I've spent some time to compute them on my own. I couldn't find all of the data used by the paper, but I've computed three different likelihood ratio estimates which I hope will be helpful to people reading this paper.

The first is comparing the exponential and linear growth models exactly as I've presented them above on US TFP data since 1954. Both models have two free parameters, the growth rate and the standard deviation of the noise. In this case we obtain a likelihood ratio of ~ 50 favoring the linear model, which is very strong evidence that there's something wrong with the exponential growth model.

What turns out to be wrong is that the volatility of TFP growth has been declining since 1954. Economists sometimes call this "the Great Moderation", and a linear model automatically incorporates this effect while an exponential one does not. As such, for the second likelihood ratio I computed, I added an extra parameter $f$ such that the standard deviation of TFP growth at time $t$ is multiplied by a factor $\exp \left(ft\right)$. I add this extra parameter to both models, so that they now both have three free parameters instead of two.

In this second case I get a likelihood ratio of ~ 1.56 favoring the linear model. Much smaller, and shows that almost all of the performance of the linear model comes from its ability to get rid of the heteroskedasticity in growth rates. For reference, if we started at a 50% prior chance of the linear model being right, this evidence would only get us to a 61% posterior chance. So it's evidence, but overall not that strong.

What about before 1954? Here I've found it quite difficult to find reliable TFP estimates, so even though I think this practice is dubious I had to use Philippon's pseudo-TFP estimates, which he computes by taking GDP per capita estimates and raising them to a power of $2/3$. This is good because we have data from the Maddison Project on the UK's GDP per capita that goes back to the 1200s.

Philippon claims that the UK's pseudo-TFP is consistent with a piecewise linear trajectory with four pieces, or three "trend breaks". He dates these at ~ 1650, ~ 1830 and ~ 1930.

Since the piecewise linear model has a total of 11^[1] (!) parameters, it's not a surprise that it fits the data much better than an exponential model which has only 2. In order to put the models on parameter parity, I've tried to compare an exponential model with the same number of parameters and essentially the same structure of trend breaks with a linear model. Here I've run against the limits of my optimization capabilities^[2] - it seems to be quite challenging to get the SciPy optimizer to properly search over potential trend break sites. In order to be fair to Philippon's model, I've initialized both the exponential and the linear models with trend breaks at the years he identifies in his paper.

Here's the fit I've obtained as a result:

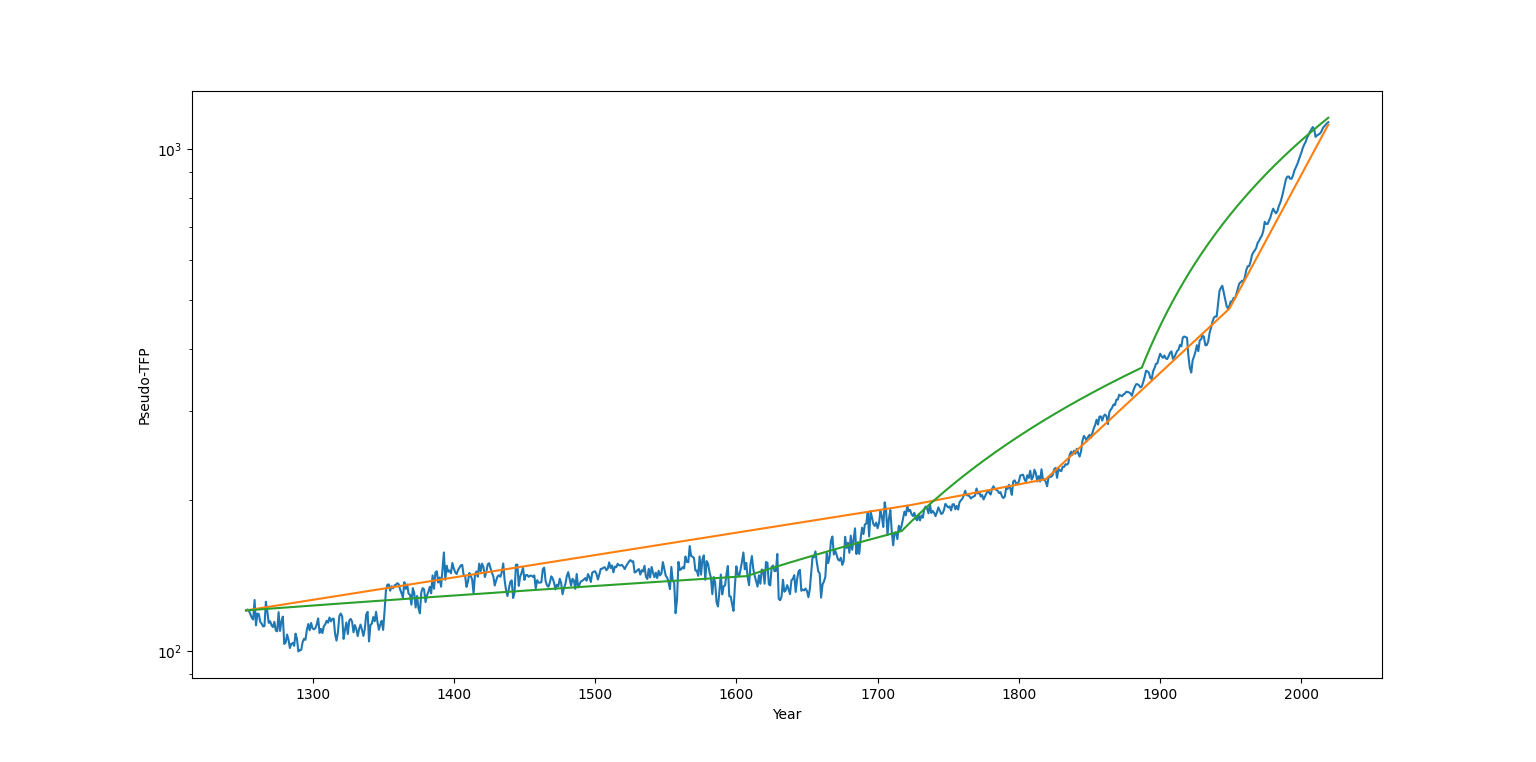
The blue line is realized pseudo-TFP in the UK, the orange line is the extrapolation of the fitted exponential model from the initial year, and the green line is the extrapolation of the linear model. Note that these are not curve fits to the blue line. The models I fit are autoregressive and I maximize the likelihood of observing the TFP at time t+1 conditional on the TFP at time t during the optimization.

As you can see, the exponential model seems to have better fit with the data despite "wasting" one of its trend breaks. This is confirmed by the likelihood ratios: the exponential fit is favored over the linear one by an astronomical likelihood factor of 3742 (!). Obviously this is misleading: once likelihood ratios get this big, the chance that the optimizer failed to find the optimal fit or that I made a mistake in my script takes over, but I'm quoting the exact figure I get just to show that the historical data doesn't seem to support Philippon's linear model.

That's all I'll say about Philippon's paper. Moving on...

What about p-values?

At first glance, it might seem like I'm wasting my time here since $p$-values are both likelihoods and probably the most universally reported statistic in science. Philippon's paper doesn't report them, but this makes it a weird exception in a world of papers that do.

The problem here is that $p$-values aren't likelihood ratios, they are just likelihoods: ones that are conditional on the null hypothesis being true. The most often used alternative hypothesis in most science papers is "the null hypothesis is false". There is an obvious issue with this: the null hypothesis is always false, so it's impossible to get useful likelihood ratios out of this frequentist methodology.

$p$-values can give us likelihood ratios if we have two hypotheses, say $H_1$ and $H_2$, that we wish to compare. We look at the probability of obtaining a result at least as extreme as what we obtained under both hypotheses, and their ratio tells us how much we should update away from one and towards the other based on this evidence. It doesn't tell us the posterior probabilities since this depends on our views about hypotheses other than $H_1$ and $H_2$, but it tells us how we should update the ratio $P\left(H_1\right)/P\left(H_2\right)$.

In the case that these are models then they represent a whole class of hypotheses that are parametrized (usually) by some finite dimensional real vector space, and then we also have to control for the fact that us fitting the models to the data artificially raises the likelihood of the data conditional on the models to some extent. This is what model selection criteria are for.

Unfortunately this is not how $p$-values are often used, which means it's quite tricky to back out likelihood ratios from most scientific papers. As I said, a Bayesian has to do this in order to update their beliefs, so the difficulty of doing it is at least a significant theoretical obstacle to efficient belief updating. In practice it's not as big of a problem because I wouldn't trust likelihood ratios reported by most papers to begin with, and there are indeed parapsychology papers that get overwhelming likelihood ratios in favor of their paranormal findings.

Still, I'd like to see more reporting of likelihood ratios by papers in cases where there's a clear discrete and small set of models that are being compared with one another. Philippon's paper is almost a perfect example of a situation where they would've been useful, which makes his decision not to report them all the more baffling to me.

---

1. Three parameters for the dates of the trend breaks, four parameters for the growth rate in each trend, four more parameters for the volatility in each trend. 4+4+3 = 11. ↩︎

2. If there are any experts on doing maximum likelihood estimation on weird distributions in Python reading the post, you can leave a comment or send me a private message. I'll send you what I've done so far and ask for advice on how to fit the models better to the data. ↩︎