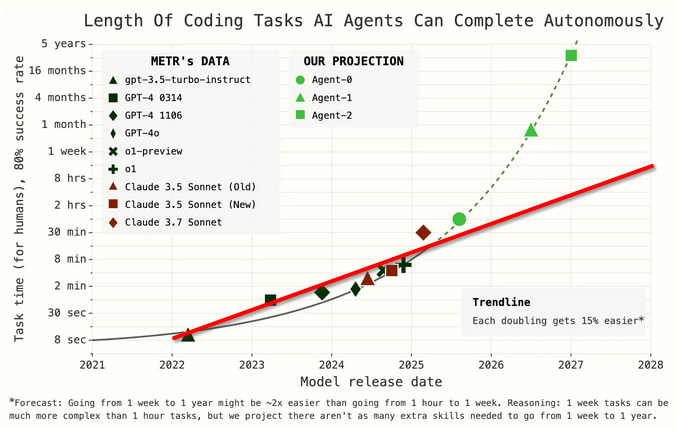
Upcoming Changes in Large Language Models
If you work in AI, then probably none of this is new to you, but if you’re curious about the near future of this technology, I hope you find this interesting! Reinforcement Learning in LLMs Large Language Models (LLMs) have shown impressive results in the past few years. I’ve noticed there’s some uncertainty among my friends about how far they’ll be able to go. A lot of the criticism of LLMs has centered on how it’s not able to pursue its own goals, and I want to argue that that won’t be a limitation for very long. What would it look like for an LLM to pursue a goal? Here are some examples of how that might go: * Goal: Maintain tone or topic in a conversation. E.g. to keep a human involved in a long and happy discussion about their life * Goal: Persuade a human operator to take some action, such as buy a product * Goal: Solve a problem through reasoning. In this case, the reward for the model would come from a sense of resolution, or being told by the human operator that their problem has been solved * Goal: Accomplish something on a website, such as find and buy concert tickets on an unfamiliar website You can probably imagine other cases in which an AI might use language to pursue some goal, whether through conversation, social media, or online posting. Reinforcement Learning There’s a whole branch of Machine Learning called Reinforcement Learning (RL), and it’s all about how to pursue goals. Modern RL has some impressive results. For years, it’s been able to play Atari games, and now it can learn to play those games in about the same number of trials as a human requires. Recently, Dreamer v3 has been able to mine diamonds in Minecraft, which I’m told is not easy for a beginner. Dreamer version 2 playing Atari games Large language models can be connected to RL. This is something that’s actively being worked on. Reinforcement Learning with Human Feedback is being done right now, which is how OpenAI gets ChatGPT to avoid talking about sensitive topics
Here's Tex Johnston talking about the manuever.
"What do you think you were doing up there?"
"I was selling airplanes"
While the president of Boeing was allegedly quite upset, Eddie Rickenbacker, the head of Eastern Airlines, was a WW1 flying ace and allegedly said "You slow-rollin' S.O.B. Why didn't you let me know? I would have been riding the jump seat". So the manuever may indeed have sold some airplanes.