Suppose we had a hypothetical 'ideal' SAE which exhaustively discovered all of the features represented by a model at a certain layer in their most 'atomic' form. Each latent's decoder direction is perfectly aligned with its respective feature direction. Zero reconstruction error, with all latents having clear, interpretable meaning. If we had such an SAE for each component of a model at each layer this would obviously be extremely valuable since we could use them to do circuit analysis and basically understand how the model works. Sure it might still be painstaking and maybe we'd wish that some of the features weren't so atomic or something, but basically we'd be in a good position to understand what's going on.
I'm not sure that even an ideal SAE like that would fare well in this evaluation. Here are some reasons why:
- The evaluation uses the same model layer on all tasks. While this layer was best on average for the baselines, it's likely that for some/many of the tasks, the model doesn't linearly represent the most relevant features at this layer, and therefore neither would a perfect SAE, resulting in poor k-sparse probing performance using the SAE. Baseline methods can still potentially perform decently on such tasks as they can combine many features which are somewhat correlated with the task and/or 'craft' more relevant features using non-linearities.
- For some tasks, the model might not linearly represent super relevant features at any layer, again limiting the performance we can expect from even a perfect SAE with k-sparse probing. For example, it feels unlikely that models such as Gemma-2-9B would linearly represent whether the second half of a prompt is entailed by the first half, unless maybe if they were prompted to look out for this (idk this might be a bad example). Again, baseline methods can still attain decent performance by combining many weakly relevant features and using non-linearities.
- Some tasks might be sufficiently complex as to naturally decompose into a combination of many (rather than few) atomic features. In such cases, the concept may be linearly represented at the layer in question, but since it's composed of many atomic features, k-sparse probing with a perfect SAE will still struggle due to the limited k while baseline methods can learn to combine arbitrarily many features.
If even an ideal SAE could realistically underperform baselines in this evaluation setup then I'm not sure we should update too heavily in terms of SAE utility for arguably their primary use cases (things like circuit discovery where we don't already know what we're looking for). Of course anyone who was planning to use SAEs for probing under data scarcity conditions etc should update more substantially based on these results.
Regarding some features not being learnt at all, I was anticipating this might happen when some features activate much more rarely than others, potentially incentivising SAEs to learn more common combinations instead of some of the rarer features. In order to potentially see this we'd need to experiment with more variations as mentioned in my other comment
Nice work! I was actually planning on doing something along these lines and still have some things I'd like to try.
Interestingly your SAEs appear to be generally failing to even find optimal solutions w.r.t the training objective. For example in your first experiment with perfectly correlated features I think the optimal solution in terms of reconstruction loss and L1 loss combined (regardless of the choice of the L1 loss weighting) would have the learnt feature directions (decoder weights) pointing perfectly diagonally. It looks like very few of your hyperparameter combinations even came close to this solution.
My post was concerned primarily with the training objective being misaligned with what we really want, but here we're seeing an additional problem of SAEs struggling to even optimise for the training objective. I'm wondering though if this might be largely/entirely a result of the extremely low dimensionality and therefore very few parameters causing them to get stuck in local minima. I'm interested to see what happens with more dimensions and more variation in terms of true feature frequency, true feature correlations, and dictionary size. And orthogonality loss may have more impact in some of those cases.
Nice, that's promising! It would also be interesting to see how those peaks are affected when you retrain the SAE both on the same target model and on different target models.
Thanks, that's very interesting!
Testing it with Pythia-70M and few enough features to permit the naive calculation sounds like a great approach to start with.
Closest neighbour rather than average over all sounds sensible. I'm not certain what you mean by unique vs non-unique. If you're referring to situations where there may be several equally close closest neighbours then I think we can just take the mean cos-sim of those neighbours, so they all impact on the loss but the magnitude of the loss stays within the normal range.
Only on features that activate also sounds sensible, but the decoder weights of neurons that didn't activate would need to be allowed to update if they were the closest neighbours for neurons that did activate. Otherwise we could get situations where e.g. one neuron (neuron A) has encoder and decoder weights both pointing in sensible directions to capture a feature, but another neuron has decoder weights aligned with neuron A but has encoder weights occupying a remote region of activation space and thus rarely activates, causing its decoder weights to remain in that direction blocking neuron A if we don't allow it to update.
Yes I think we want to penalise high cos-sim more. The modified sigmoid flattens out as x->1 but the I think the purple function below does what we want.
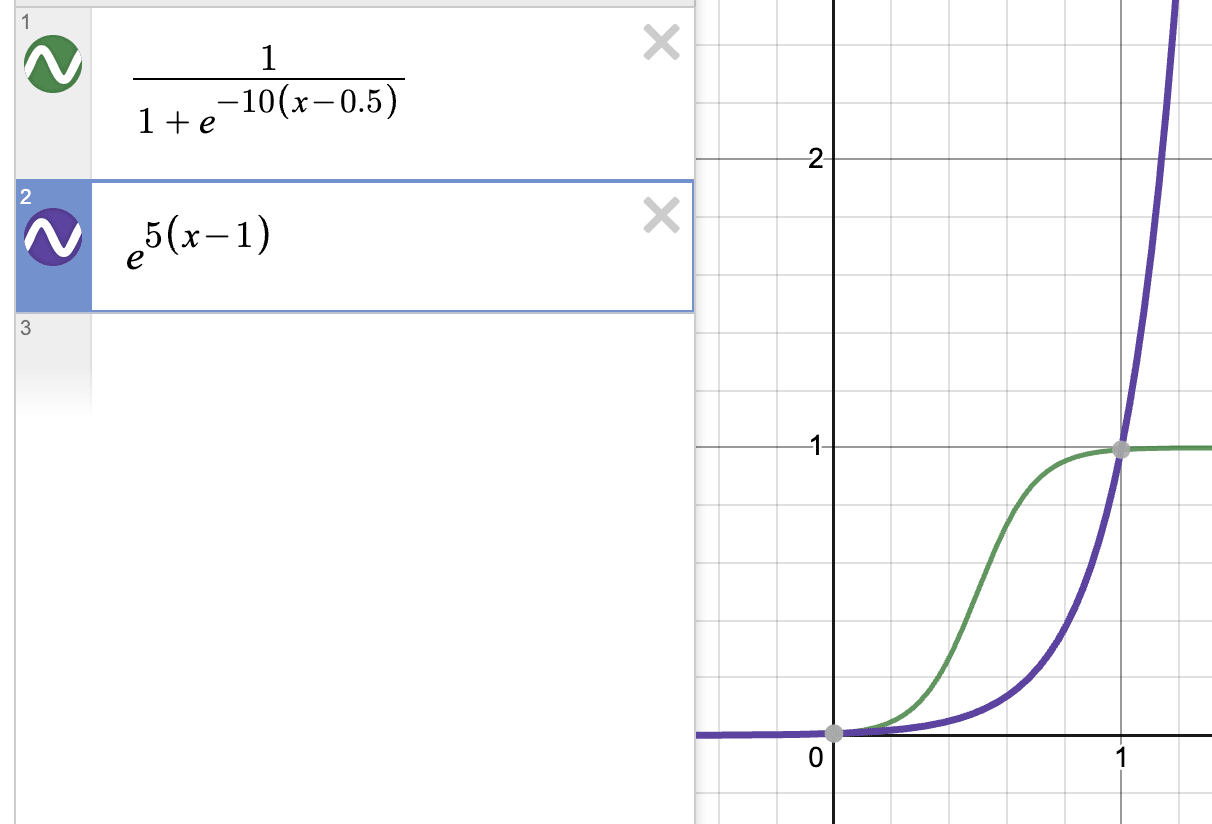
Training with a negative orthogonality regulariser could be an option. I think vanilla SAEs already have plenty of geometrically aligned features (e.g. see @jacobcd52 's comment below). Depending on the purpose, another option to intentionally generate feature combinatorics could be to simply add together some of the features learnt by a vanilla SAE. If the individual features weren't combinations then their sums certainly would be.
I'll be very interested to see results and am happy to help with interpreting them etc. Also more than happy to have a look at any code.
Thanks for clarifying! Indeed the encoder weights here would be orthogonal. But I'm suggesting applying the orthogonality regularisation to the decoder weights which would not be orthogonal in this case.
Thanks, I mentioned this as a potential way forward for tackling quadratic complexity in my edit at the end of the post.
Regarding achieving perfect reconstruction and perfect sparsity in the limit, I was also thinking along those lines i.e. in the limit you could have a single neuron in the sparse layer for every possible input direction. However please correct me if I’m wrong but assuming the SAE has only one hidden layer then I don't think you could prevent neurons from activating for nearby input directions (unless all input directions had equal magnitude), so you'd end up with many neurons activating for any given input and thus imperfect sparsity.
Otherwise mostly agreed. Though as discussed, as well as making it necessary to figure out how to break apart feature combinations (as you said), feature splitting would also seem to incur the risk of less common “true features” not being represented even within combinations so those would get missed entirely.
Even just for evaluating the utility of SAEs for supervised probing though, I think it's unfair to use the same layer for all tasks. Afaik there could easily be tasks where the model represents the target concept using a small number of linear features at some layer, but not at the chosen layer. This will harm k-sparse SAE probe performance far more than the baseline performance because the baselines can make the best of the bad situation at the chosen layer by e.g. combining many features which are weakly correlated with the target concept and using non-linearities. I think it would be a fair test if the 'quiver of arrows' were expanded to include each method applied at each of a range of layers.