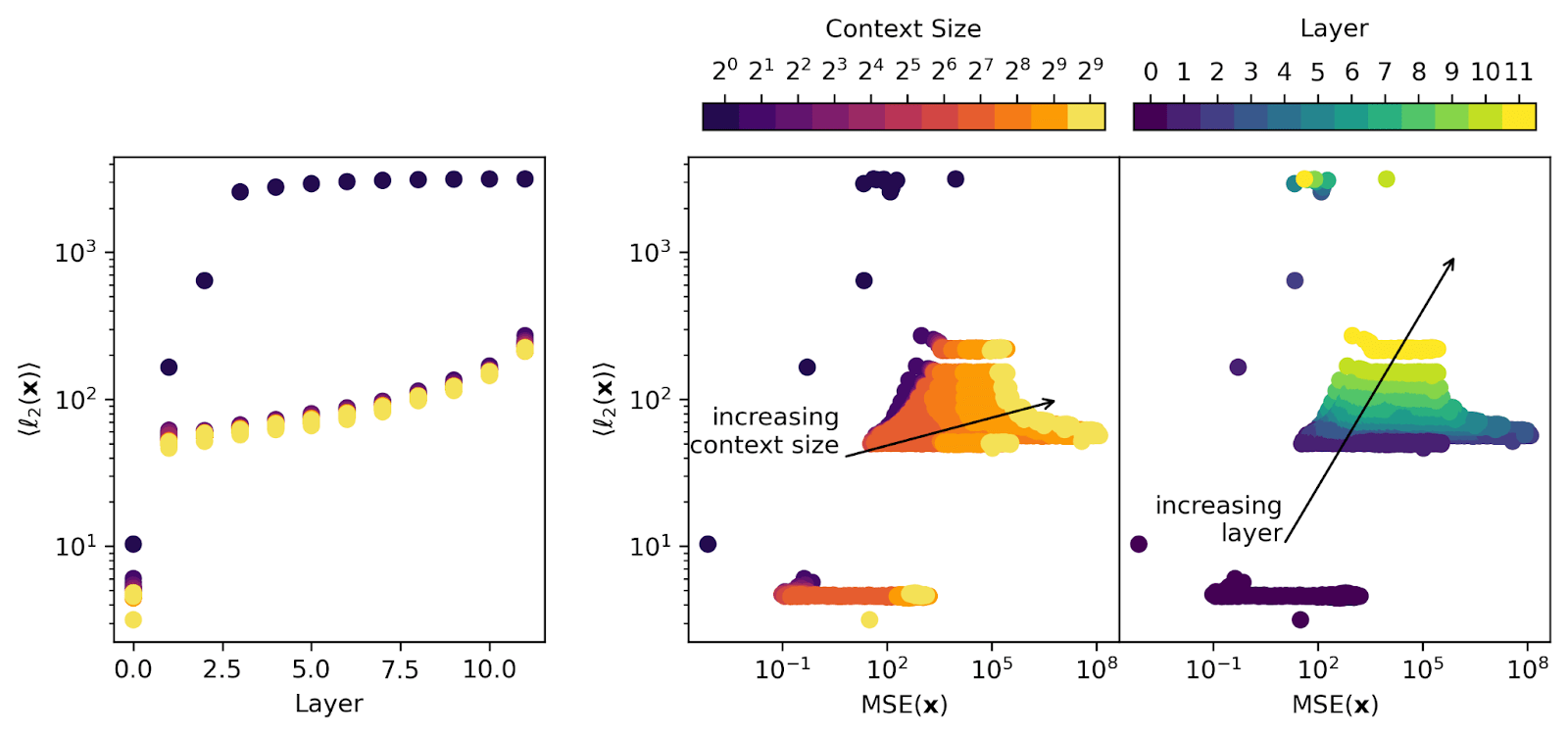
Note: The second figure in this post originally contained a bug pointed out by @LawrenceC, which has since been fixed. Summary * Sparse Autoencoders (SAEs) reveal interpretable features in the activation spaces of language models, but SAEs don’t reconstruct activations perfectly. We lack good metrics for evaluating which parts of model activations SAEs fail to reconstruct, which makes it hard to evaluate SAEs themselves. In this post, we argue that SAE reconstructions should be tested using well-established benchmarks to help determine what kinds of tasks they degrade model performance on. * We stress-test a recently released set of SAEs for each layer of the gpt2-small residual stream using randomly sampled tokens from Open WebText and the Lambada benchmark where the model must predict a specific next token. * The SAEs perform well on prompts with context sizes up to the training context size, but their performance degrades on longer prompts. * In contexts shorter than or equal to the training context, the SAEs that we study generally perform well. We find that the performance of our late-layer SAEs is worse than early-layer SAEs, but since the SAEs all have the same width, this may just be because there are more features to resolve in later layers and our SAEs don’t resolve them. * In contexts longer than the training context, SAE performance is poor in general, but it is poorest in earlier layers and best in later layers. Introduction Last year, Anthropic and EleutherAI/Lee Sharkey's MATS stream showed that sparse autoencoders (SAEs) can decompose language model activations into human-interpretable features. This has led to a significant uptick in the number of people training SAEs and analyzing models with them. However, SAEs are not perfect autoencoders and we still lack a thorough understanding of where and how they miss information. But how do we know if an SAE is “good” other than the fact that it has features we can understand? SAEs try to reco