Thanks for your thoughtful comment! I think that's an interesting idea. If a replacement model is faithful, you would indeed expect it to behave similar when tested on other data. This may possibly connect to a related finding that we couldn't yet explain: that CLTs fail for memorized sequences, when those should be the simplest. Maybe the OOD test is something that we could do in real LLMs as well, not just toy models.
I don't think I'd go as far as saying "faithfulness==OOD generalization" though. I think it is possible that two different circuits produce the same behavior, even on OOD. For example, let model A and B learn to multiplicate arbitrary numbers perfectly. There are different ways to do x * y, for example compute +x y times, do it like we learned in school, etc. In those cases, OOD examples would still deliver equal output but the internal circuits are different. So I'd say that faithfulness is a stronger claim than OOD generalization.
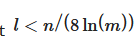
Calculating l, the maximal number of simultaneously active features, yields strange results. For example, if we have 100 features and 100 neurons, l has to be < 100/(8 * ln(100)) = 2.7. But I would expect that 100 features can be simultaneously active because we have 100 dimensions, so the features can be orthogonal and independent. Am I understanding something wrong?
Thanks for your comment, I really appreciate it!
(a) I claim we cannot construct a faithful one-layer CLT because the real circuit contains two separate steps! What we can do (and we kinda did) is to have a one-layer CLT to have perfect reconstruction always and everywhere. But the point of a CLT is NOT to have perfect reconstruction - it's to teach us how the original model solved the task.
(b) I think that's the point of our post! That CLTs miss middle-layer features. And that this is not a one-off error but that the sparsity loss function incentivizes solutions that miss middle-layer features. We are working on adding more case studies to make this claim more robust.