Thanks for the very clear reply. I like your decomposition of CAFT into (1) ablating activations and (2) ablating gradients.

To isolate effect (1), we can test a variant of CAFT where we detach the projection before we subtract it from the activations, such that the gradients through the subspace are not ablated.
...
We did this experiment on the two models used in the paper: for one of them, this version performs slightly worse but similarly to CAFT and, for the other one, it doesn’t reduce misalignment at all and it’s similar to regular finetuning.

I predict that for the model where only-ablate-activations performed well, the ablation is actually steering towards misalignment (whereas for the other model, zero-ablation is steering away from, or orthogonally to, misalignment). I'll check this at some point in the next week or so.

I think the general technique of train-time steering seems promising enough that it's worth figuring out best practices. These best practices might depend on the task:

•  If the base model already contains circuitry that reads from the steering direction $\overrightarrow{v}$ and produces the bad behavior (as is the case with EM) then preventative steering seems to make sense.
• But if the base model does not already have that circuitry, perhaps we should just mean-ablate the $\overrightarrow{v}$ direction, making it harder for the bad circuitry to be learnt in the first place.

Ofc, this is pure speculation. I just want to highlight the fact that there seems to be a lot still to be understood.

To begin talking about volume, you first need to really understand what space is.

No, stop it, this is a terrible approach to math education. "Ok kids, today we're learning about the area of a circle. First, recall the definition of a manifold." No!! 

Persona Vectors notes a confusing aspect of CAFT (see appendix J.1):

We hypothesize that CAFT’s effectiveness in the evil and sycophancy cases stems from the fact that forcing activations to have zero projection effectively acts as positive preventative steering (because of the initial negative projections in the base model).

I agree with them. Zero-ablating a subspace is unprincipled, since the residual stream has no preferred origin. The practical consequence is that for behaviors, like EM, that can be triggered by adding a constant steering vector $\overrightarrow{v}$, CAFT's zero-ablation may actually increase the component along $\overrightarrow{v}$ and thus steer towards the behavior. 

I think (though I may have missed something) that the CAFT paper gives no evidence for whether zero-ablation steers towards or away from EM, so it is hard to compare its results with those of Persona Vectors. You could resolve this confusion by:

1) Checking whether zero-ablation increases or decreases the activations of "misaligned" SAE latents
2) Checking whether zero-ablating the base model leads to more or less misaligned responses (note: no training involved).

I really thought I'd updated all the way towards "models linearly represent everything". But somehow I was still surprised by Dmitrii's training order result.

LLMs linearly represent the accuracy of their next-token predictions

A quick experiment I did on Llama-3.2-1B:

• Choose a layer, and let ${\overrightarrow{x}}_t$ be that layer's residual activation at token position $t$.
• Let $l_t^{\left(\text{correct}\right)}$ be the logit at position $t$ that was assigned to whatever turned out to be the correct next token (i.e. the correct token at position $t+1$).
• Use least-squares to fit a linear map that takes ${\overrightarrow{x}}_t$ and predicts $l_{t-1}^{\left(\text{correct}\right)}$.

Results for each layer are below. Layers in the second half of the model (except the last layer) have decent ($R^2>0.6$) linear representations of the correct logit.

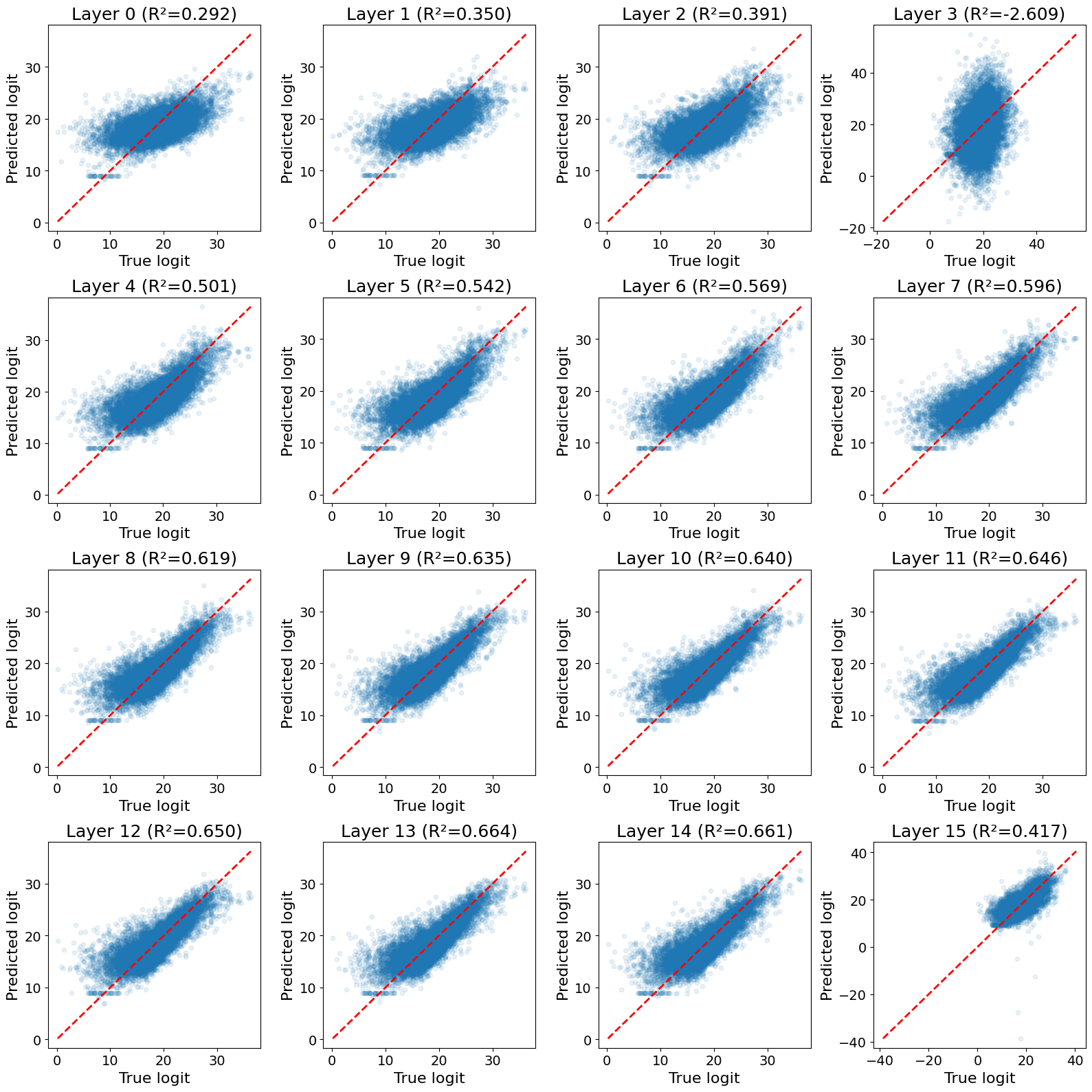
I don't find this result very surprising. I checked it because I thought it might explain what's going on in this very cool recent paper by @Dmitrii Krasheninnikov , Richard Turner and @David Scott Krueger (formerly: capybaralet)). They finetune Llama-3.2-1B and show that the model linearly represents the order of appearance of finetuning data. If more recent data has lower loss, then perhaps my probing results explain theirs.

Ah I hadn't noticed that, very nice. Great post!

In case anyone else didn't know what it meant for a set of binary strings to be "prefix-free", here's Claude's explanation, which I found helpful:
 

A set of binary strings is prefix-free if no string in the set is a prefix of any other string in the set.

Example:

• ✅ Prefix-free: {0, 10, 110, 111}
• ❌ Not prefix-free: {0, 01, 10} (because "0" is a prefix of "01")

Why does this matter for Turing machines?

The key is in how universal Turing machines work. A universal machine U simulates any other machine T by receiving input of the form i′q, where:

• i′ = prefix-free encoding of machine T's description
• q = the actual input to feed to machine T

U must parse this concatenated input to figure out: "Where does the machine description end and the actual input begin?"

Without prefix-free encoding: Given input "00101", U can't tell if the machine description is "0", "00", "001", etc. - there's ambiguity.

With prefix-free encoding: Once U reads a complete machine description, it knows exactly where that description ends and the input begins. No ambiguity, no delimiters needed.

This unique parseability is essential for universal machines to correctly simulate other machines, and it's crucial for Kolmogorov complexity theory where we need to measure program lengths precisely without parsing ambiguity.
 

Operationalizing the definition of a shard

Pope and Turner (2022) define a shard as follows:

A shard of value refers to the contextually activated computations which are downstream of similar historical reinforcement events.

To operationalize their definition, we must decide exactly what we mean by contextually activated computations, and by similar reinforcement events. One could philosophize here, but I'll just pick somewhat-arbitrary definitions and run with them, for the sake of quickly producing something I could turn into code.

Following Apollo/Goodfire, I will identify contextually activated computations with certain directions in parameter space. These directions might be found using APD, L3D, SPD, or some future method.

I am not sure when to consider two reinforcement events (i.e. RL reward-assignments) "similar". But if we replace "reinforcement events" with "RL updates", there is a natural definition:  cluster RL parameter updates, and call two updates similar if they are in the same cluster. A given update should be allowed to be in multiple clusters, and we suspect parameter updates enjoy some linear structure. Therefore, a natural clustering method is an SAE.^[1] Then, a shard is a decoder vector of an SAE trained on RL parameter updates.

Annoyingly, parameter vectors much larger than the activation vectors that SAEs are usually trained on, posing three potential issues:

1. Storing enough parameter updates to train our SAE on takes a ton of memory.
2. The SAE itself has a ton of parameters - too many to effectively train.
3. It may be impossible to reconstruct parameter updates with reasonable sparsity (with $L_0\sim 100$, say, like standard SAEs).

To mitigate Issue 1, one could focus on a small subset of model parameters. One could also train the SAE at the same time as RL training itself, storing only a small buffer of the most recent parameter updates.

L3D cleverly deals with Issue 2 using low-rank parametrizations for the encoder and decoder of the SAE.

Issue 3 may turn out not to occur in practice. Mukherjee et al (2025) find that, when post-training an LLM with RL, parameter updates are very sparse in the neuron basis. Intuitively, many expect that such post-training merely boosts/suppresses a small number of pre-existing circuits. So perhaps we will find that, in practice, one can reconstruct parameter updates with reasonable sparsity.

All of this is to say: maybe someone should try training an SAE/applying L3D to RL parameter updates. And, if they feel like it, they could call the resulting feature vectors "shards".

1. ^{^}

   For each SAE latent, the corresponding cluster is the set of data points on which that latent is active.

2. ^{^}

   Shard theory is supposed to apply to humans, too, but here I focus on NNs since humans seem more complicated.

Some issues with the ICL Superposition paper

Setup:

Xiong et al (2024) show that LLMs can in-context-learn several tasks at once. Consider e.g. the following prompt:

France -> F
Portugal -> Portuguese
Germany -> Berlin
Spain -> Madrid
Russia -> R
Poland -> Polish
Italy ->

A model will complete this prompt sometimes with Rome, sometimes with I, and sometimes with Italian, learning a "superposition" of the country -> capital, country -> first-letter and country -> language tasks. (I wish they hadn't used this word: the mech interp notion of superposition is unrelated).

Let $D_i$ be the proportion of the in-context examples that correspond to task $i$, and let $P_i$ be the probability that the model completes the prompt according to task $i$. Call a model calibrated if $P_i\approx D_i$: the probability it assigns to a task is proportional to the number of times the task appeared in-context. A measure of the degree of calibration is given by the KL-divergence:

$KL\left(D||P\right)={\sum }_i{D}_i\log \left(D_i/P_i\right).$

Lower KL means better calibration. 

Issue 1:

The authors show that, for a certain set of 6 tasks, and with 60 in-context examples, calibration improves with model size:
 

The best reported KL between the uniform distribution [0.167, 0.167, ..., 0.167] and the model's output distribution is around 1.5. To give a sense for what this means, here are four examples of distributions with such a KL:

$P_1=[0.004,0.004,0.004,0.33,0.33,0.33]$

$P_2=[0.02,...,0.02,0.9]$

$P_3=[{10}^{-5},0.19999,...,0.19999]$

$P_4=[0.004,0.008,0.016,0.032,0.2,0.74]$.

Seeing these distributions convinced me that the models they studied are not well-calibrated. I felt a bit misled by the paper.

Issue 2:

Say we take turns with the model, repeatedly appending a new "question" (e.g. a country) to the prompt and allowing the model to generate an "answer" (e.g. the country's capital, language, or first letter) at default temperature 1.0. The authors state:

After the first token is generated, the model tends to converge on predicting tokens for a single task, effectively negating its ability for multi-task execution.

But this sort of mode-collapse behavior is not what we would observe from a well-calibrated model!

For simplicity, consider the case of only two tasks: $A$ and $B$. Let $n_A$ and $n_B$ be the number of examples of each task, prior to a given generation step. A calibrated model generates $A$ with probability $\frac{n_A}{n_A+n_B}$, in which case $(n_A,n_B)\leftarrow (n_A+1,n_B)$. Otherwise, it generates $B$, and $(n_A,n_B)\leftarrow (n_A,n_B+1)$. 

This is precisely the Pólya urn model. If the numbers of each task are initially $A_0$ and $B_0$, and then we generate for a long time, it can be shown that the limiting proportion of $A$ tasks is a random variable $X$ distributed as follows:

In the realistic setting where $A_0,B_0>1$, this distribution is peaked around$\frac{A_0-1}{A_0+B_0-2}$, i.e. roughly the proportion of the initial tasks that were $A$, and goes to zero at $x=0$ or $1$. So calibrated models don't collapse; they tend to maintain roughly the initial ratio of tasks.

My intuition at least for the single word case is that saying a word increases the probability the model will say it in future. Therefore, if it wants the probability it says that the future to be low, it's incentivised not to say it anywhere.

I share your intuition, and think you are describing what we called "conditional spillover".^[1] The fact that the Mind+Face intervention did not fully prevent spillover in our experiments is some evidence that conditional spillover is occurring.

One might mitigate conditional spillover as follows. In REINFORCE, the usual parameter update is (setting batch size = lr = 1 for brevity, and being a little schematic):

$\delta \theta =r\left(\underset{g_{\text{CoT}}}{\underset{}{{\nabla }_{\theta }\log p_{\theta }(\text{CoT}}}\right)+\underset{g_{\text{out}}}{\underset{}{{\nabla }_{\theta }\log p_{\theta }\left(\text{output | CoT}\right)}})$.

Here, $r$ is the reward, which depends only on the output. In the case where $r$ is the sum of a task-completion and an obfuscation-inducing term (as in our current work), we can write:

$\delta \theta =(r_{\text{task}}+r_{\text{obfusc}})(g_{\text{CoT}}+g_{\text{out}})$.

In order to mitigate conditional spillover, we can simply modify the gradient update by removing the $r_{\text{obfusc}}\times g_{\text{CoT}}$ term:

$(\delta \theta {)}_{\text{modified}}=r_{\text{task}}{g}_{\text{CoT}}+(r_{\text{task}}+r_{\text{obfusc}})g_{\text{out}}$.

If this mitigation is used in combination with Mind+Face, then the Mind is not reinforced for producing CoTs which increase the probability of output obfuscation. It is only reinforced for task completion.

1. ^{^}

   Side note: I don't love our "conditional spillover" and "parametric spillover" terminology, since they sound like different observed effects, whereas they are really two different (proposed) mechanisms underlying the same observed effect. If brevity weren't an issue, I'd call them "spillover due to later tokens conditioning on earlier ones" and "spillover due to parameter sharing between the models generating CoT and output", or something.