Posts
Wikitag Contributions
I agree with this critique; I think washing machines belong on the "light bulbs and computers" side of the analogy. The analogy has the form:
"germline engineering for common diseases and important traits" : "gene therapy for a rare disease" :: "widespread, transformation uses of electricity" : x
So x should be some very expensive, niche use of electricity that provides a very large benefit to its tiny user base (and doesn't arguably indirectly lead to large future benefits, e.g. via scientific discovery for a niche scientific instrument).
Something I didn't realize until now: P = NP would imply that finding the argmax of arbitrary polynomial time (P-time) functions could be done in P-time.
Proof sketch
Suppose you have some polynomial time function f: N -> Q. Since f is P-time, if we feed it an n-bit input x it will output a y with at most max_output_bits(n) bits as output, where max_output_bits(n) is at most polynomial in n. Denote y_max and y_min as the largest and smallest rational numbers encodable in max_output_bits(n) bits.
Now define check(x, y) := f(x) >= y, and argsat(y) := x such that check(x, y) else None. argsat(y) is in FNP, and thus runs in P-time if P = NP. Now we can find argmax(f(x)) by running a binary search over all values y in [y_min, y_max] on the function argsat(y). The binary search will call argsat(y) at most max_output_bits(n) times, and P x P = P.
I'd previously thought of argmax as necessarily exponential time, since something being an optimum is a global property of all evaluations of the function, rather than a local property of one evaluation.
- The biggest discontinuity is applied at the threshold between spike and slab. Imagine we have mutations that before shrinkage have the values +4 IQ, +2 IQ, +1.9 IQ, and 1.95 is our spike vs. slab cutoff. Furthermore, let's assume that the slab shrinks 25% of the effect. Then we get 4→3, 2→1.5, 1.9→0, meaning we penalize our +2 IQ mutation much less than our +1.9 mutation, despite their similar sizes, and we penalize our +4 IQ effect size more than the +2 IQ effect size, despite it having the biggest effect, this creates an arbitrary cliff where similar-sized effects are treated completely differently based on which side of the cutoff they fall on, and where the one that barely makes it, is the one we are the least skeptical off"
There isn't any hard effect size cutoff like this in the model. The model just finds whatever configurations of spikes have high posteriors given the assumption of sparse normally distributed nonzero effects. I.e., it will keep adding spikes until further spikes can no longer offset their prior improbability via higher likelihood (note this isn't a hard cutoff, since we're trying to approximate the true posterior over all spike configurations; some lower probability configurations with extra spikes will be sampled by the search algorithm).
My guess is that peak intelligence is a lot more important than sheer numbers of geniuses for solving alignment. At the end of the day someone actually has to understand how to steer the outcome of ASI, which seems really hard and no one knows how to verify solutions. I think that really hard (and hard to verify) problem solving scales poorly with having more people thinking about it.
Sheer numbers of geniuses would be one effect of raising the average, but I'm guessing the "massive benefits" you're referring to are things like coordination ability and quality of governance? I think those mainly help with alignment via buying time, but if we're already conditioning on enhanced people having time to grow up I'm less worried about time, and also think that sufficiently widespread adoption to reap those benefits would take substantially longer (decades?).
Emotional social getting on with people vs logic puzzle solving IQ.
Not sure I buy this, since IQ is usually found to positively correlate with purported measures of "emotional intelligence" (at least when any sort of ability (e.g. recognizing emotions) is tested; the correlation seems to go away when the test is pure self reporting, as in a personality test). EDIT: the correlation even with ability-based measures seems to be less than I expected.
Also, smarter people seem (on average) better at managing interpersonal issues in my experience (anecdotal, I don't have a reference). But maybe this isn't what you mean by "emotional social getting on with people".
There could have been a thing where being too far from the average caused interpersonal issues, but very few people would have been far from the average, so I wouldn't expect this to have prevented selection if IQ helped on the margin.
Engineer parents are apparently more likely to have autistic children. This looks like a tradeoff to me. To many "high IQ" genes and you risk autism.
Seems somewhat plausible. I don't think that specific example is good since engineers are stereotyped as aspies in the first place; I'd bet engineering selects for something else in addition to IQ that increases autism risk (systematizing quotient, or something). I have heard of there being a population level correlation between parental IQ and autism risk in the offspring, though I wonder how much this just routes through paternal age, which has a massive effect on autism risk.
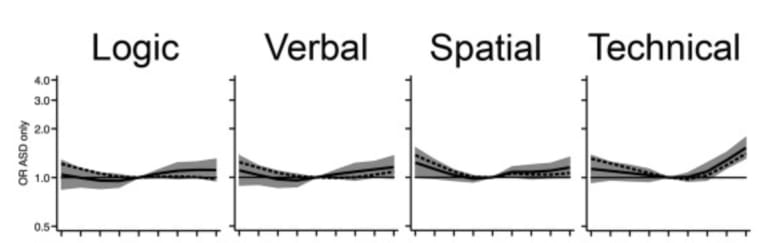
This study found a relationship after controlling for paternal age (~30% risk increase when father's IQ > 126), though the IQ test they used had a "technical comprehension" section, which seems unusual for an IQ test (?), and which seems to have driven most of the association.
How many angels can dance on the head of a pin. In the modern world, we have complicated elaborate theoretical structures that are actually correct and useful. In the pre-modern world, the sort of mind that now obsesses about quantum mechanics would be obsessing about angels dancing on pinheads or other equally useless stuff.
So I think there's two possibilities here to keep distinct. (1) is that ability to think abstractly wasn't very useful (and thus wasn't selected for) in the ancestral environment. (2) Is that it was actively detrimental to fitness, at least above some point. E.g. because smarter people found more interesting things to do than reproduce, or because they cared about the quality of life of their offspring more than was fitness-optimal, or something (I think we do see both of these things today, but I'm not sure about in the past).
They aren't mutually exclusive possibilities; in fact if (2) were true I'd expect (1) to probably be true also. (2) but not (1) seems unlikely since IQ being fitness-positive on the margin near the average would probably outweigh negative effects from high IQ outliers.
So on one hand, I sort of agree with this. For example, I think people giving IQ tests to LLMs and trying to draw strong conclusions from that (e.g. about how far off we are from ASI) is pretty silly. Human minds share an architecture that LLMs don't share with us, and IQ tests measure differences along some dimension within the space of variation of that architecture, within our current cultural context. I think an actual ASI will have a mind that works quite differently and will quickly blow right past the IQ scale, similar to your example of eagles and hypersonic aircraft.
On the other hand, humans just sort of do obviously vary a ton in abilities, in a way we care about, despite the above? Like, just look around? Read about Von Neumann? Get stuck for days trying to solve a really (subjectively) hard math problem, and then see how quickly someone a bit smarter was able to solve it? One might argue this doesn't matter if we can't feasibly find anyone capable of solving alignment inside the variation of the human architecture. But Yudkowsky, and several others, with awareness and understanding of the problem, exist; so why not see what happens if we push a bit further? I sort of have this sense that once you're able to understand a problem, you probably don't need to be that much smarter to solve it, if it's the sort of problem that's amenable to intelligence at all.
On another note: I can imagine that, from the perspective of evolution in the ancestral environment, that maybe human intelligence variation appeared "small", in that it didn't cache out in much fitness advantage; and it's just in the modern environment that IQ ends up conferring massive advantages in ability to think abstractly or something, which actually does cache out in stuff we care about.
I'm sort of confused by the image you posted? Von Neumann existed, and there are plenty of very smart people well beyond the "Nerdy programmer" range.
But I think I agree with your overall point about IQ being under stabilizing selection in the ancestral environment. If there was directional selection, it would need to have been weak or inconsistent; otherwise I'd expect the genetic low hanging fruit we see to have been exhausted already. Not in the sense of all current IQ-increasing alleles being selected to fixation, but in the sense of the tradeoffs becoming much more obvious than they appear to us currently. I can't tell what the tradeoffs even were: apparently IQ isn't associated with the average energy consumption of the brain? The limitation of birth canal width isn't a good explanation either since IQ apparently also isn't associated with head size at birth (and adult brain size only explains ~10% of the variance in IQ).
I'm looking for recommendations for frameworks/tools/setups that could facilitate machine checked math manipulations.
More details: