The ‘strong’ feature hypothesis could be wrong
NB. I am on the Google Deepmind language model interpretability team. But the arguments/views in this post are my own, and shouldn't be read as a team position. > “It would be very convenient if the individual neurons of artificial neural networks corresponded to cleanly interpretable features of the input. For example, in an “ideal” ImageNet classifier, each neuron would fire only in the presence of a specific visual feature, such as the color red, a left-facing curve, or a dog snout” > - Elhage et. al, Toy Models of Superposition Recently, much attention in the field of mechanistic interpretability, which tries to explain the behavior of neural networks in terms of interactions between lower level components, has been focussed on extracting features from the representation space of a model. The predominant methodology for this has used variations on the sparse autoencoder, in a series of papers inspired by Elhage et. als. model of superposition.It's been conventionally understood that there are two key theories underlying this agenda. The first is the ‘linear representation hypothesis’ (LRH), the hypothesis that neural networks represent many intermediates or variables of the computation (such as the ‘features of the input’ in the opening quote) as linear directions in it’s representation space, or atoms[1]. And second, the theory that the network is capable of representing more of these ‘atoms’ than it has dimensions in its representation space, via superposition (the superposition hypothesis). While superposition is a relatively uncomplicated hypothesis, I think the LRH is worth examining in more detail. It is frequently stated quite vaguely, and I think there are several possible formulations of this hypothesis, with varying degrees of plausibility, that it is worth carefully distinguishing between. For example, the linear representation hypothesis is often stated as ‘networks represent features of the input as directions in representation space’. H

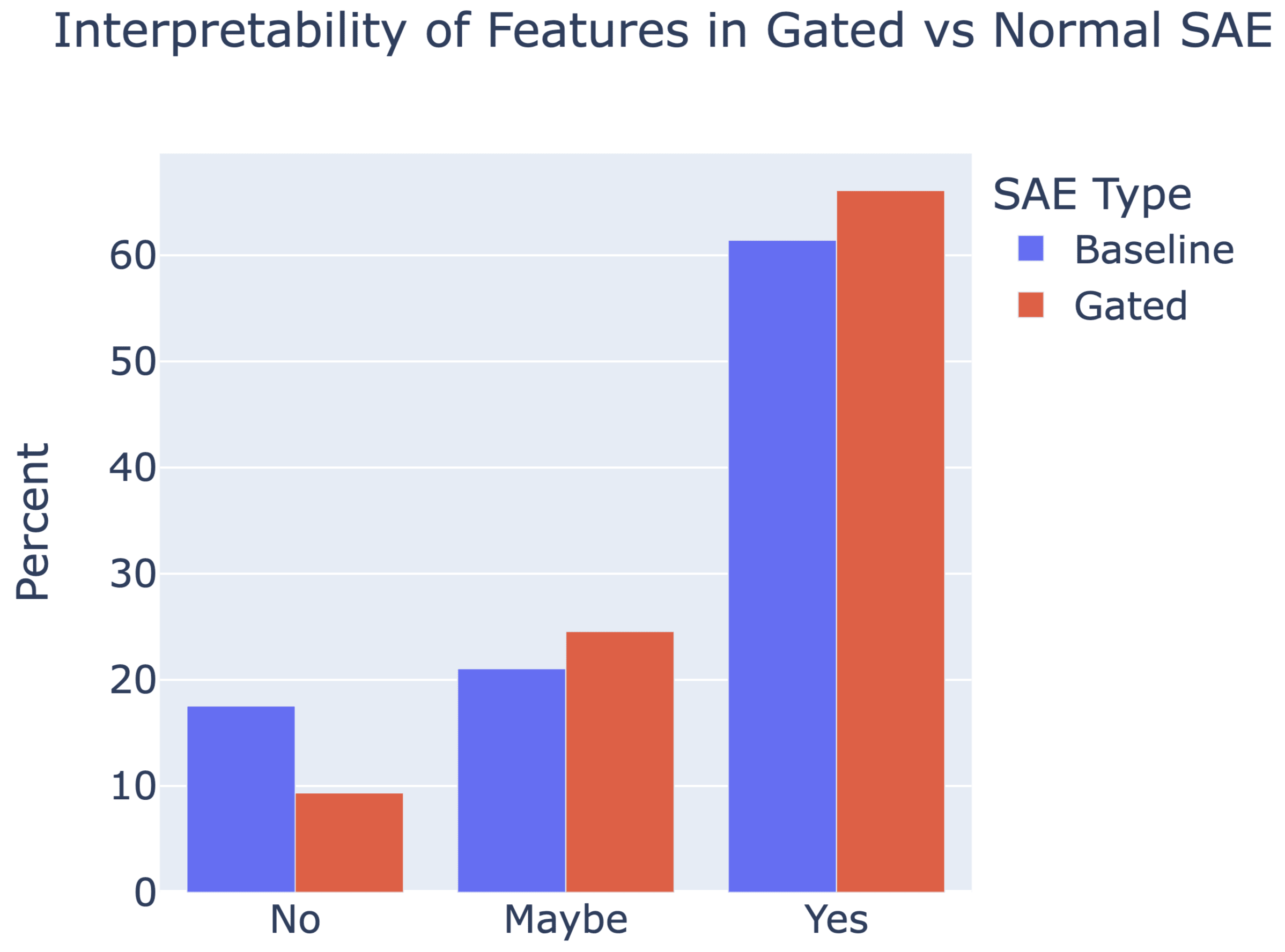
I think that the general argument I made in this post was correct, and anticipated a shift away from the strong feature hypothesis mode of thinking on SAEs. It’s hard to say the degree to which this was downstream of me publishing this post(probably mostly not? though it may have had some influence) but it probably deserves some Bayes points nevertheless. I think that many of the arguments in this post continue to influence my thinking, and there is a lot in the post that remains valuable.
In fact, if anything I think I should have been a bit more confident; the strong feature hypothesis is wrong would have been a better title.... (read 676 more words →)