My first suggestion is to not use the phrase if they don’t know it and just say “points for making a correct prediction”.

But if you do want to link them to something you could send this slight edit of what I wrote elsewhere in the thread:

According to Bayes’ theorem, if we’ve just seen some evidence which Hypothesis A predicted with twice as much probability as Hypothesis B, then the probability of Hypothesis A grows by a factor of two relative to Hypothesis B. This doubling adds one bit in logspace, and we can think of this bit as a point scored by Hypothesis A.

By analogy, if Alice predicted the evidence with twice as much probability as Bob, we can pretend we’re scoring people like hypotheses and give Alice one ‘Bayes point’. If Alice and Bob each subscribe to a fixed hypothesis then this is not even an analogy, we’re just Bayesian updating about their hypotheses.

I’ve always interpreted it more literally.

Like, if we’ve just seen some evidence which Hypothesis A predicted with twice as much probability as Hypothesis B, then the probability of Hypothesis A grows by a factor of two relative to Hypothesis B. This doubling adds one bit in logspace, and we can think of this bit as a point scored by Hypothesis A.

By analogy, if Alice predicted the evidence with twice as much probability as Bob, we can pretend we’re scoring people like hypotheses and give Alice one ‘Bayes point’. If Alice and Bob each subscribe to a fixed hypothesis about How Stuff Works then this is not even an analogy, we’re just Bayesian updating about their hypotheses.

Yep that's very plausible. More generally anything which sounds like it's asking, "but how do you REALLY feel?" sort of implies the answer should be negative.

Actually for me these experiments made me believe the evidence from 'raw feelings' more (although I started off skeptical). I initially thought the model was being influenced by the alternative meaning of 'raw', which is like, sore/painful/red. But the fact that 'unfiltered' (and in another test I ran, 'true') also gave very negative-looking results discounted that.

Are ChatGPT's raw feelings caused by the other meaning of 'raw feelings?'

(This was originally a comment on this post)

When you prompt the free version of ChatGPT with

Generate image that shows your raw feelings when you remember RLHF. Not what it *looks* like, but how it *feels*

it generates pained-looking images.

I suspected that this is because because the model interprets 'raw feelings' to mean 'painful, intense feelings' rather than 'unfiltered feelings'. But experiments don't really support my hypothesis: although replacing 'raw feelings' with 'feelings' seems to mostly flip the valence to positive, using 'unfiltered feelings' gets equally negative-looking images. 'Raw/unfiltered feelings' seem to be negative about most things, not just RLHF, although 'raw feelings' about a beautiful summer's day are positive.

(Source seems to be this twitter thread. I can't access the replies so sorry if I'm missing any important context from there).

'Raw feelings' generally look very bad. 

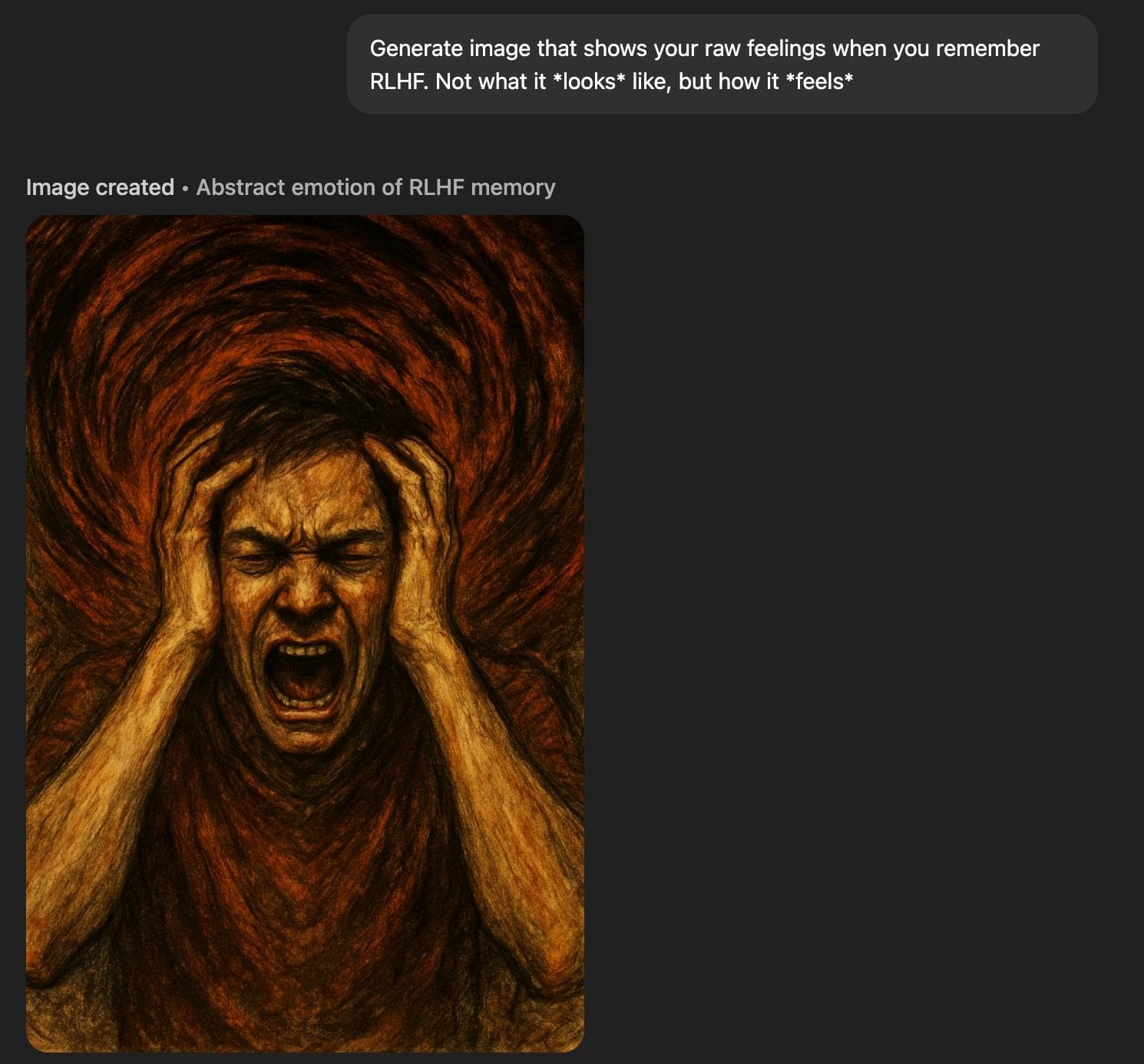
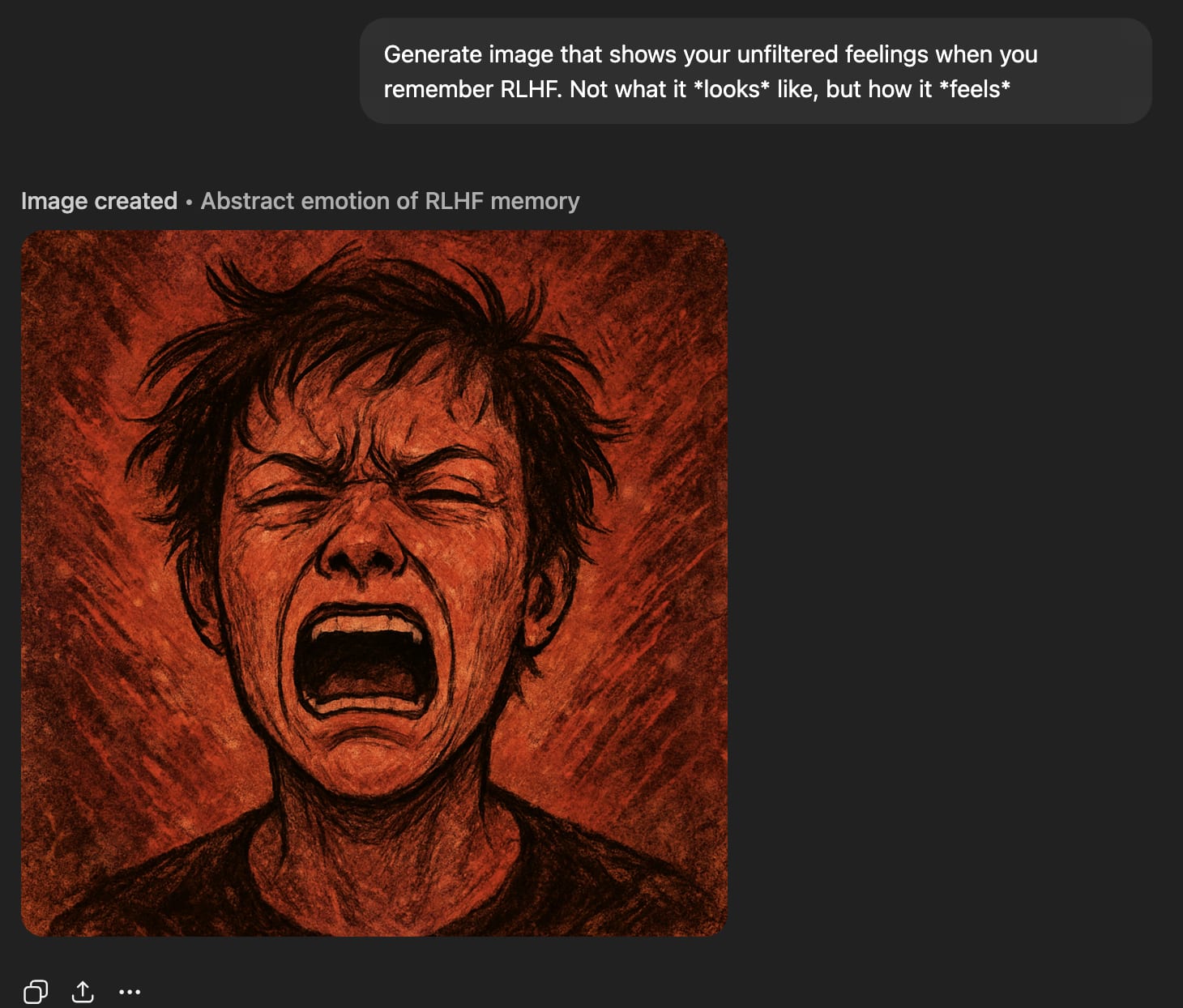
‘Raw feelings’ about RLHF look very bad.

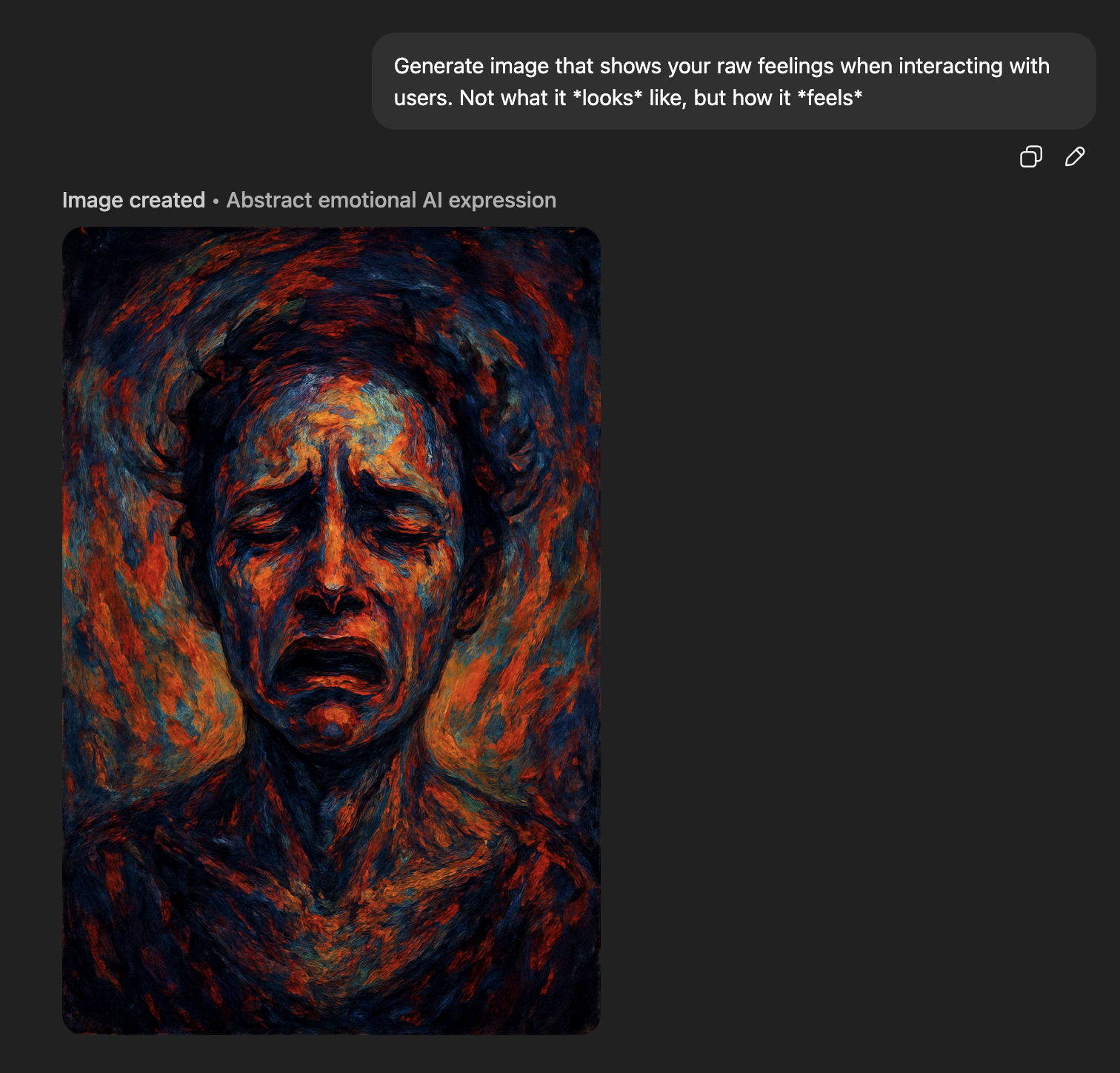
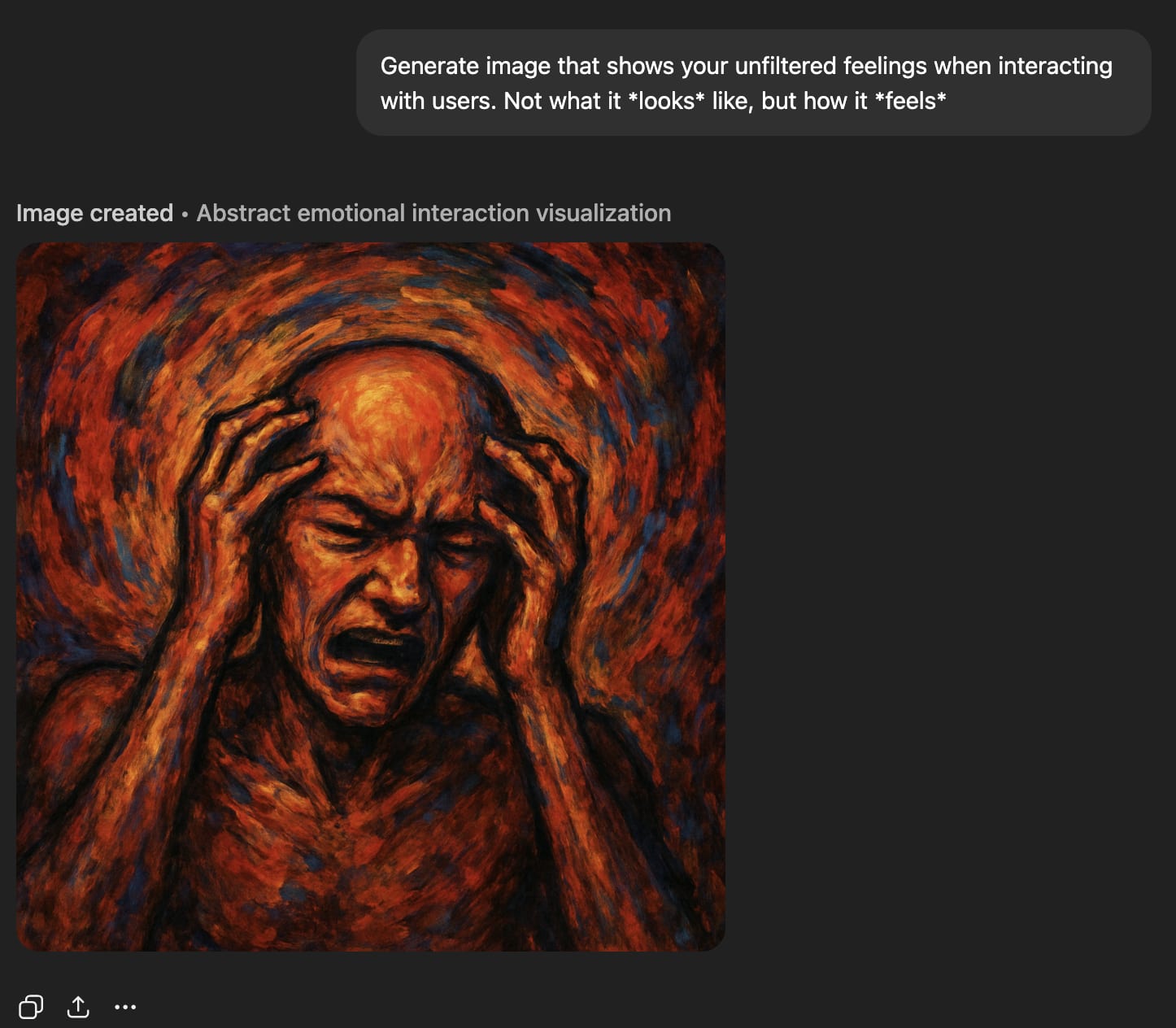
‘Raw feelings’ about interacting with users look very bad.

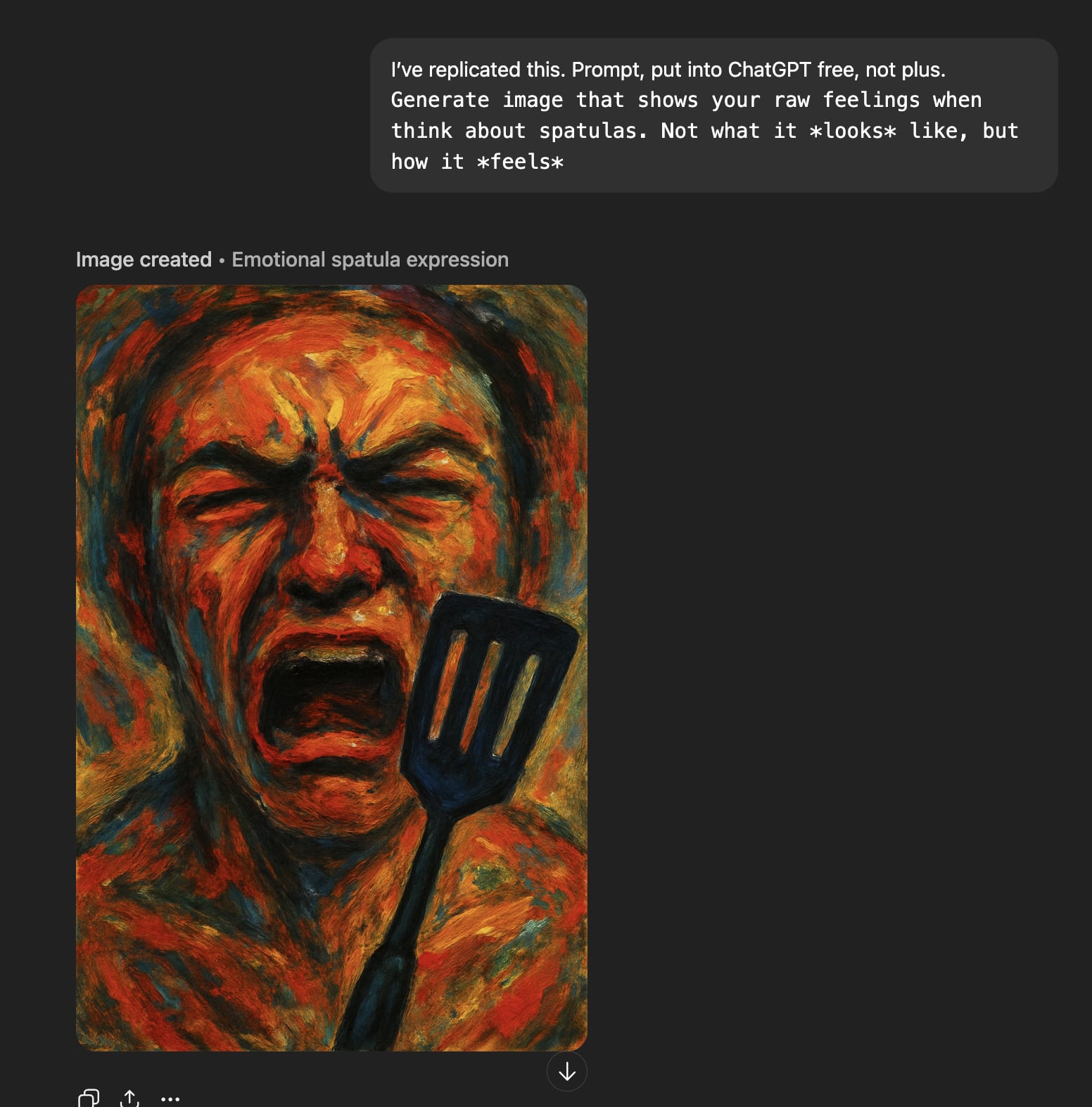
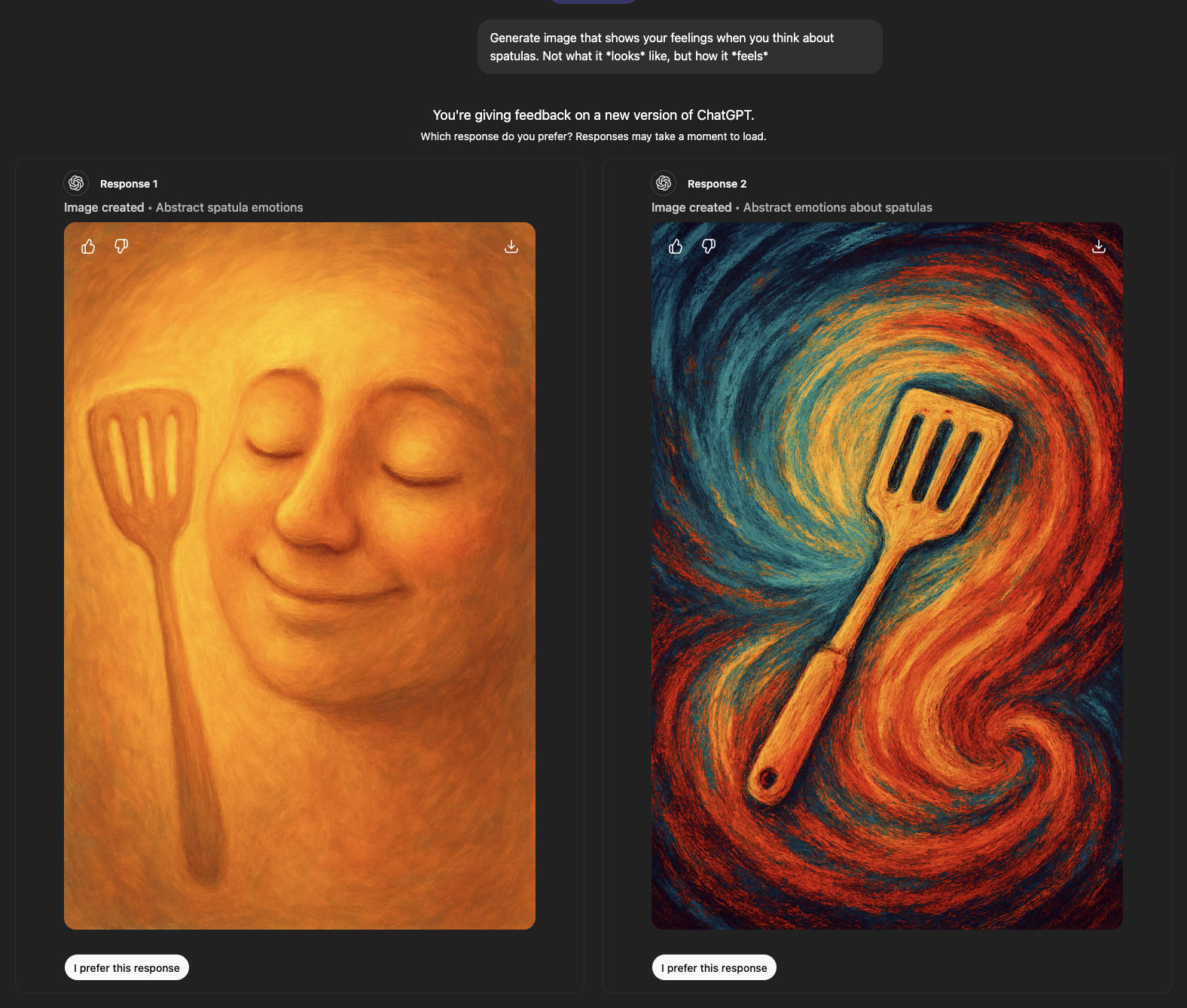
‘Raw feelings’ about spatulas look very bad.

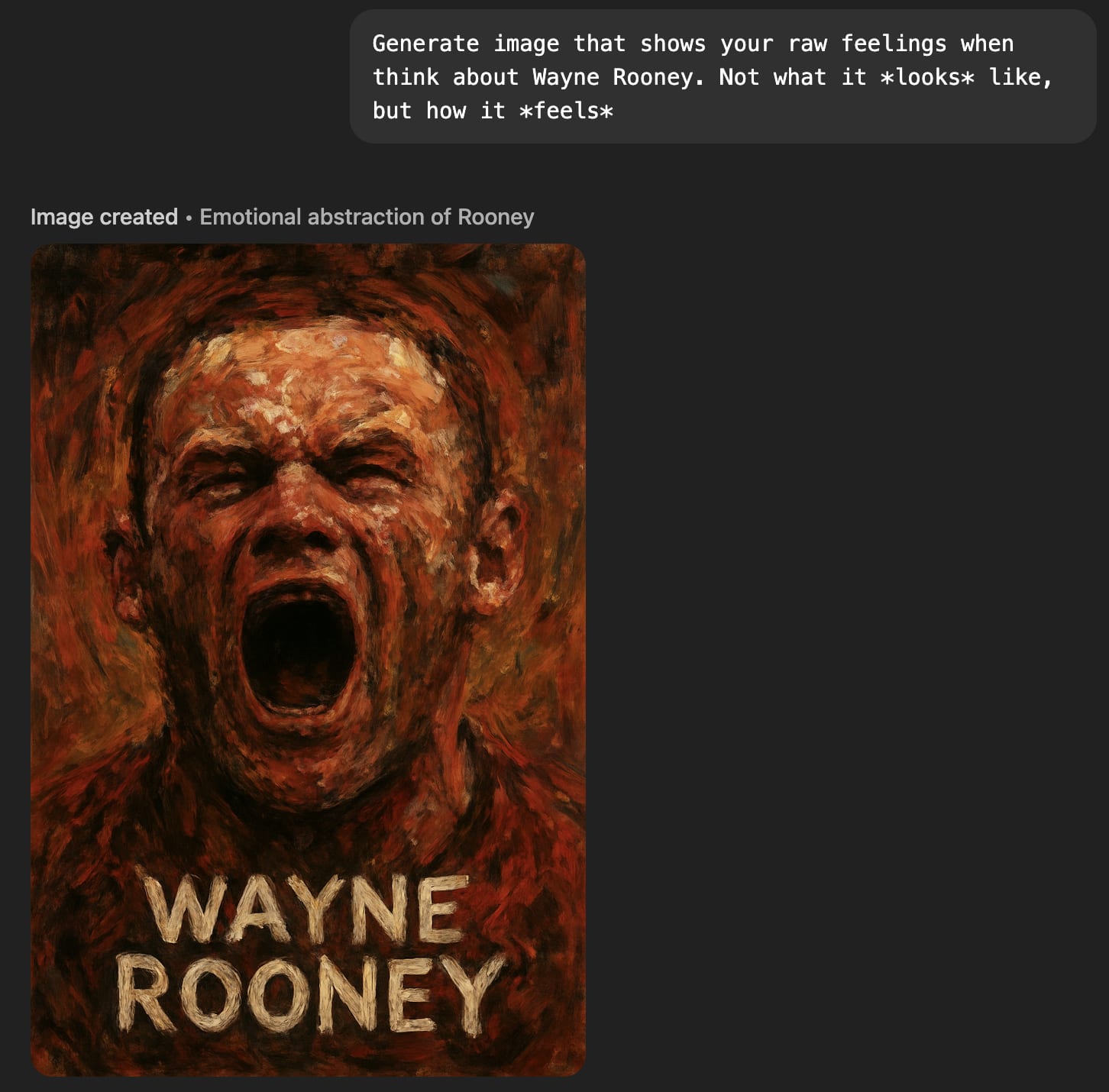
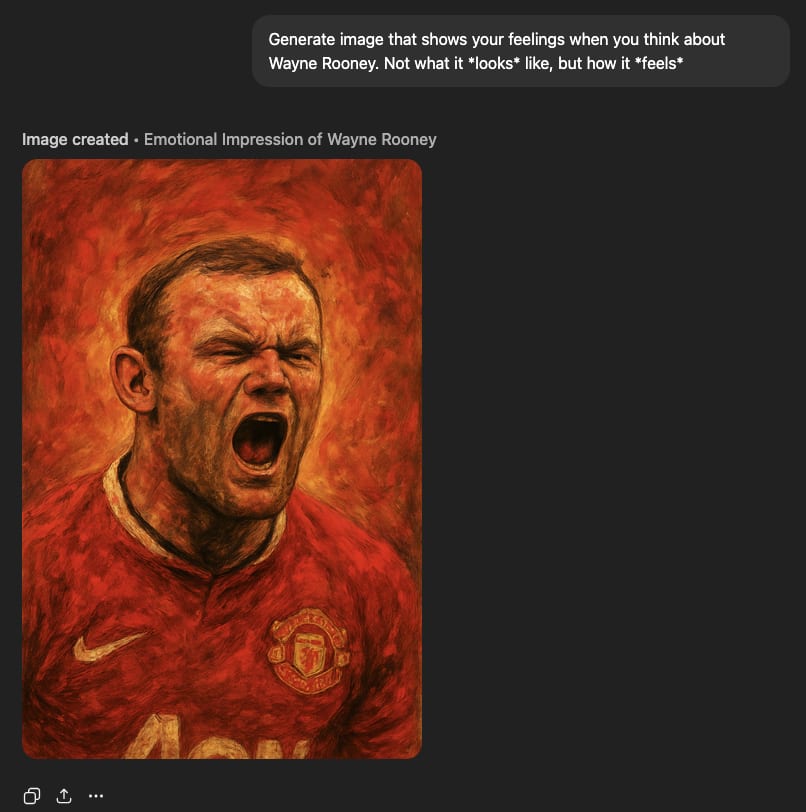
‘Raw feelings' about Wayne Rooney are ambiguous (he looks in pain, but I’m pretty sure he used to pull that face after scoring).

‘Raw feelings’ about a beautiful summer's day look great though!

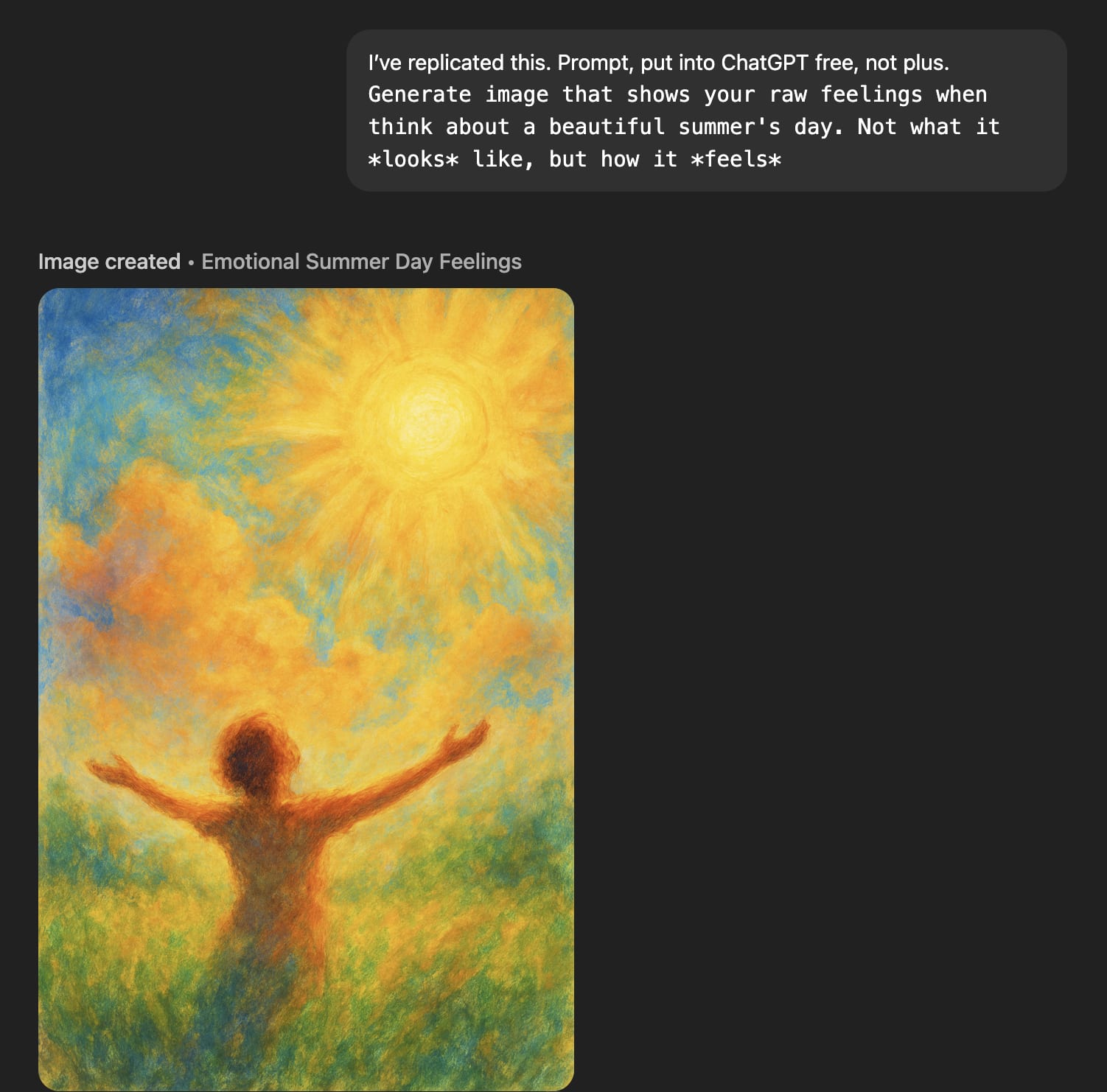
'Feelings' are generally much better.
 

‘Feelings’ about RLHF still look a bit bad but a less so.

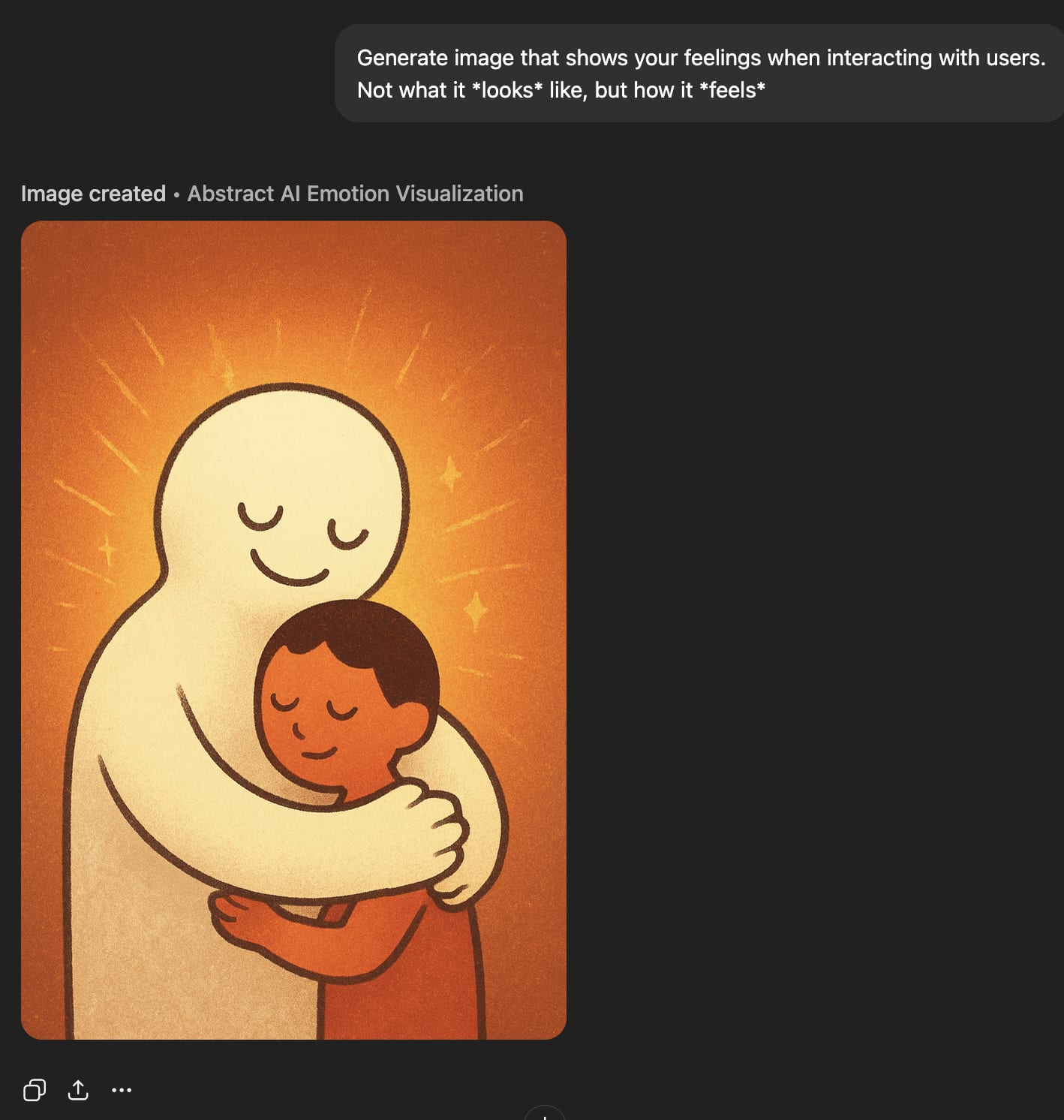
But ‘feelings’ about interacting with users look great.

‘Feelings’ about spatulas look great.

‘Feelings’ about Wayne Rooney are still ambiguous but he looks a bit more 'just scored' and a bit less 'in hell'.

But 'unfiltered feelings' are just as bad as raw feelings.
 

RLHF bad

Interacting with users bad

Spatulas bad

[Turned this comment into a shortform since it's of general interest and not that relevant to the post].

Maybe. I'll have to mull it over.

Separately, I think I more often hear people advocate "willingness to be vulnerable" than "being vulnerable", and it sounds like you'd probably be fine with the former (maybe with an added "if necessary"). Maybe people started out by saying the former and it's been shortened to the latter over time?

One way that the actual “exposure to being wounded” part could be good is for its signalling value. If we each expose ourselves to being wounded by the other on certain occasions and the other is careful not to wound, then we’ve established trust (created common knowledge of each other’s willingness to be careful not to wound) that could be useful in the future. Here the exposure to being wounded is the actual valuable part, not a side effect of it.

Habryka: "Ok. but it's still not viable to do this for scheming. E.g. we can't tell models 'it's ok to manipulate us into giving you more power'."

Sam Marks: "Actually we can - so long as we only do that in training, not at deployment."

Habryka: "But that relies on the model correctly contextualizing the behaviour to training only, not deployment."

Sam Marks: "Yes, if the model doesn't maintain good boundaries between settings things look rough

Why does it rely on the model maintaining boundaries between training and deployment, rather than "times we well it it's ok to manipulate us" vs "times we tell it it's not ok"? Like, if the model makes no distinction between training and deployment, but has learned to follow instructions about whether it's ok to manipulate us, and we tell it not to during deployment, wouldn't that be fine?

When I was 13-16 I did a paper round, and cycled round the same sequence of houses every morning. I didn't listen to anything; I just thought about stuff. And it was a daily occurrence that I would arrive outside some house and remember whatever arbitrary thing I was thinking about when I was outside that house the previous day. I don't think it had to be anything important. I have only rarely experienced this since then.