Free will is like temperature: a useful tool for analyzing the behavior of certain systems which are too big and complicated to model in exact detail.
If you know the positions and velocities of every atom in a box of gas, with enough compute you can predict its future to arbitrary precision; does it "have a temperature"? Irrelevant! Technically yes, I guess, but it's sorta an epiphenomenon, screened off from reality by your exact knowledge of the initial conditions and your willingness to throw compute at your model. But if you're less-than-perfectly omniscient, it might be more convenient to consider the box as having a "temperature" and model it more abstractly.
Substitute "person+environment"/"free will" for "box of gas"/"temperature" and that's all still true.
I see! Thanks for the thoughtful response. I think my problem is caused by not having brought enough neuroscience and psychology textbooks to my armchair, leaving me in too-many-plausible-hypotheses-land, rather than your too-few-. I'll take another stab at this sequence if/when I collect more background knowledge!
I've read about half of this sequence, and it's certainly the most palatable, well-founded-seeming discussion of consciousness I've ever encountered.
But... I've kind of run aground on the question: how would I tell if this is true? (Or, you know, all models are false etc., but how would I tell if this is useful?)
Three examples of how a theory can useful: "Hey, I came up with this new theory of blurtzian phenomena! ...
- Make predictions: "...The literature has catalogued 347 kinds of blurtz, but under this model, there should be at least two more, with the following characteristics: [...]"
- Distill: "...The literature has catalogued 351 kinds of blurtz with various complicated characteristics, but under this model, all those complicated characteristics are pretty closely retrodicted by modeling each of the (3^3 choose 2) blurtzes as being the interaction of [...]"
- Babble: "...The literature has a couple different models of blurtzes, all with various open questions. Here's one more. It's not obviously right, but it's another promising direction to go."
This sequence doesn't feel like (1) or (2) to me. Is it (3), or something else?
Heuristic: distrust any claim that's much memetically fitter than its retraction would be. (Examples: "don't take your vitamins with {food}, because it messes with {nutrient} uptake"; "Minnesota is much more humid than prior years because of global-warming-induced corn sweat"; "sharks are older than trees"; "the Great Wall of China is visible from LEO with the naked eye")
It sounds like you're assuming you have access to some "true" probability for each event; do I misunderstand? How would I determine the "true" probability of e.g. Harris winning the 2028 US presidency? Is it 0/1 depending on the ultimate outcome?
(Hmm. Come to think of it, if the y-axis were in logits, the error bars might be ill-defined, since "all the predictions come true" would correspond to +inf logits.)
Ah-- I took every prediction with p<0.50 and flipped 'em, so that every prediction had p>=0.50, since I liked the suggestion "to represent the symmetry of predicting likely things will happen vs unlikely things won't."
Thanks for the close attention!
I like the idea, but with n>100 points a histogram seems better, and for few points it's hard to draw conclusions. e.g., I can't work out an interpretation of the stdev lines that I find helpful.
Nyeeeh, I see your point. I'm a sucker for mathematical elegance, and maybe in this case the emphasis is on "sucker."
I'd make the starting point p=0.5, and use logits for the x-axis; that's a more natural representation of probability to me. Optionally reflect p<0.5 about the y-axis to represent the symmetry of predicting likely things will happen vs unlikely things won't.
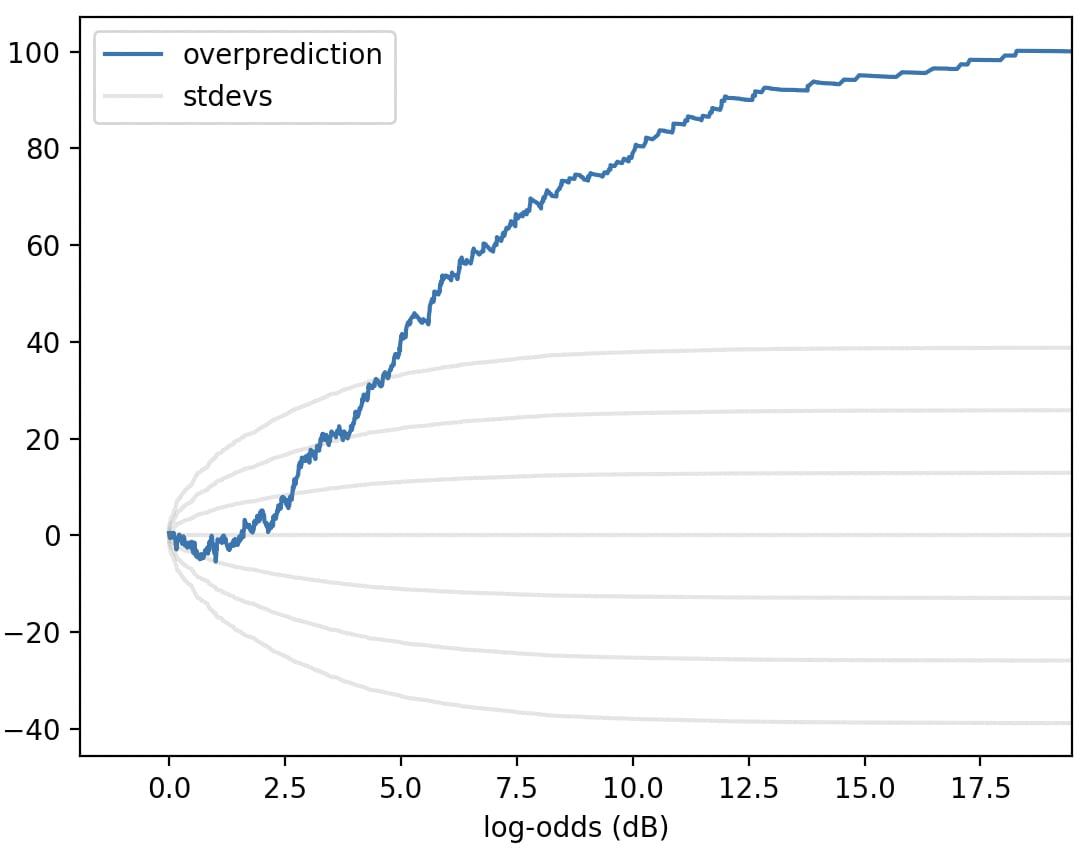
(same predictions from my last graph, but reflected, and logitified)
Hmm. This unflattering illuminates a deficiency of the "cumsum(prob - actual)" plot: in this plot, most of the rise happens in the 2-7dB range, not because that's where the predictor is most overconfident, but because that's where most of the predictions are. A problem that a normal calibration plot wouldn't share!
(A somewhat sloppy normal calibration plot for those predictions:
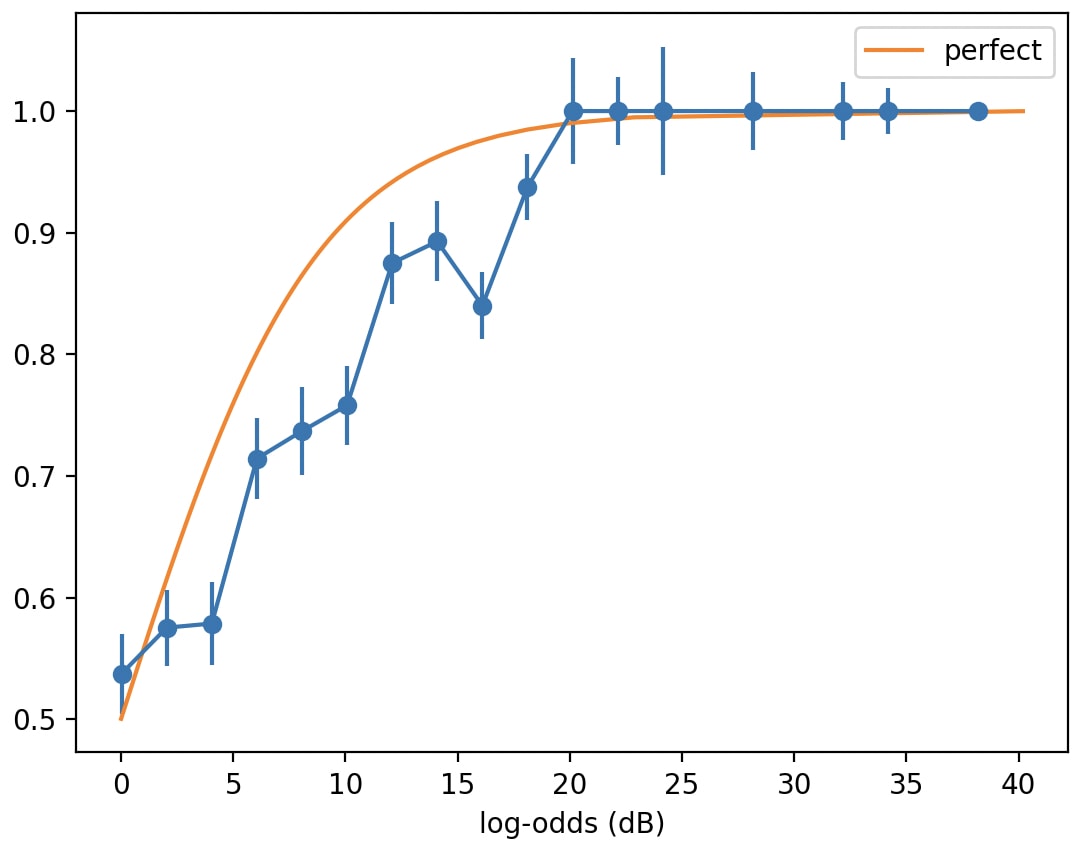
Perhaps the y-axis should be be in logits too; but I wasn't willing to figure out how to twiddle the error bars and deal with buckets where all/none of the predictions came true.)
(Tongue partly-but-not-entirely in cheek: if you painstakingly prepare a second box of gas with the exact same initial conditions as the first, it will have exactly the same temperature; corollary, if you painstakingly prepare a second person with the exact same initial conditions as the first, they will have exactly the same free will.)