This is a linkpost for https://optimizationprocess.com/calibration-cdf/
Histograms are to CDFs as calibration plots are to...
7Zac Hatfield-Dodds
6Optimization Process
4Drake Thomas
2Optimization Process
1Optimization Process
3Garrett Baker
4Optimization Process
2IlyaShpitser
1Optimization Process
New Comment
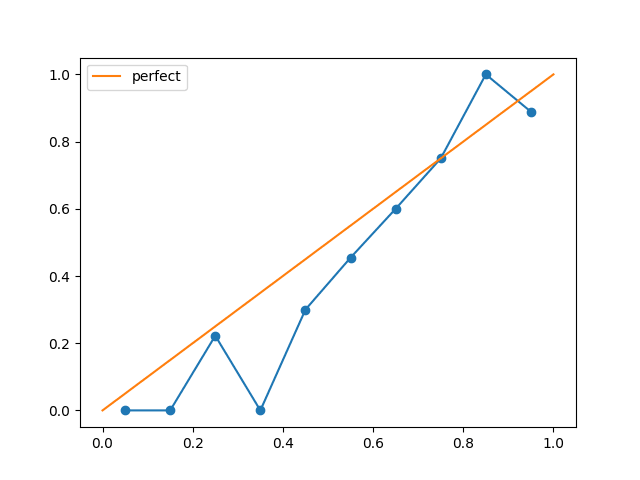
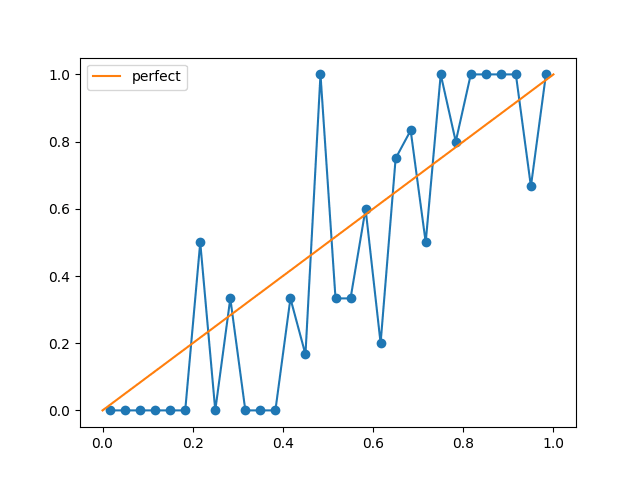
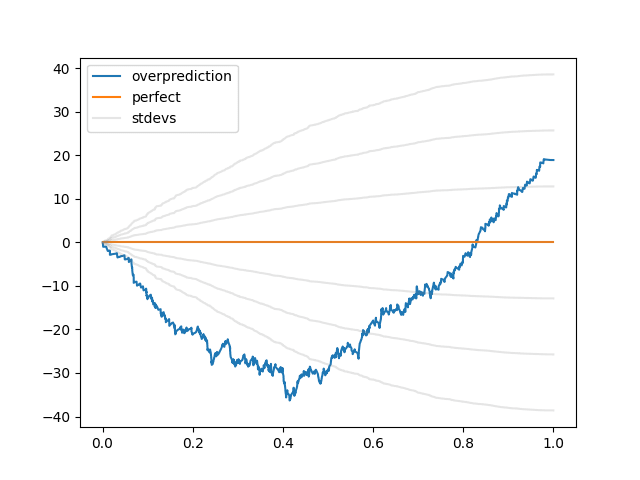
- I like the idea, but with n>100 points a histogram seems better, and for few points it's hard to draw conclusions. e.g., I can't work out an interpretation of the stdev lines that I find helpful.
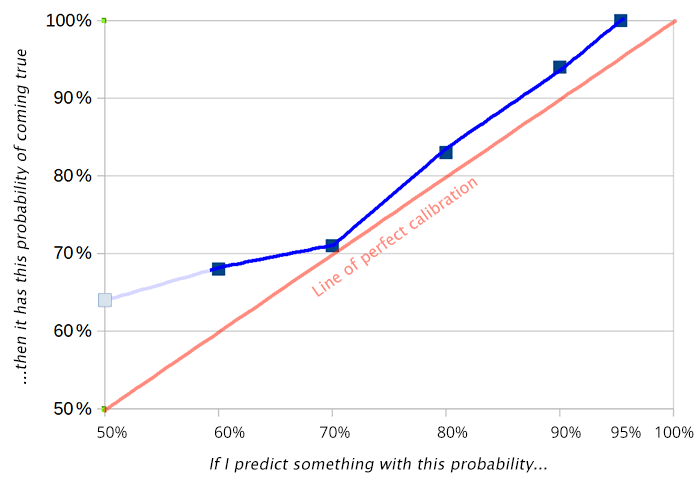
- I'd make the starting point p=0.5, and use logits for the x-axis; that's a more natural representation of probability to me. Optionally reflect p<0.5 about the y-axis to represent the symmetry of predicting likely things will happen vs unlikely things won't.
I like the idea, but with n>100 points a histogram seems better, and for few points it's hard to draw conclusions. e.g., I can't work out an interpretation of the stdev lines that I find helpful.
Nyeeeh, I see your point. I'm a sucker for mathematical elegance, and maybe in this case the emphasis is on "sucker."
I'd make the starting point p=0.5, and use logits for the x-axis; that's a more natural representation of probability to me. Optionally reflect p<0.5 about the y-axis to represent the symmetry of predicting likely things will happen vs unlikely things won't.
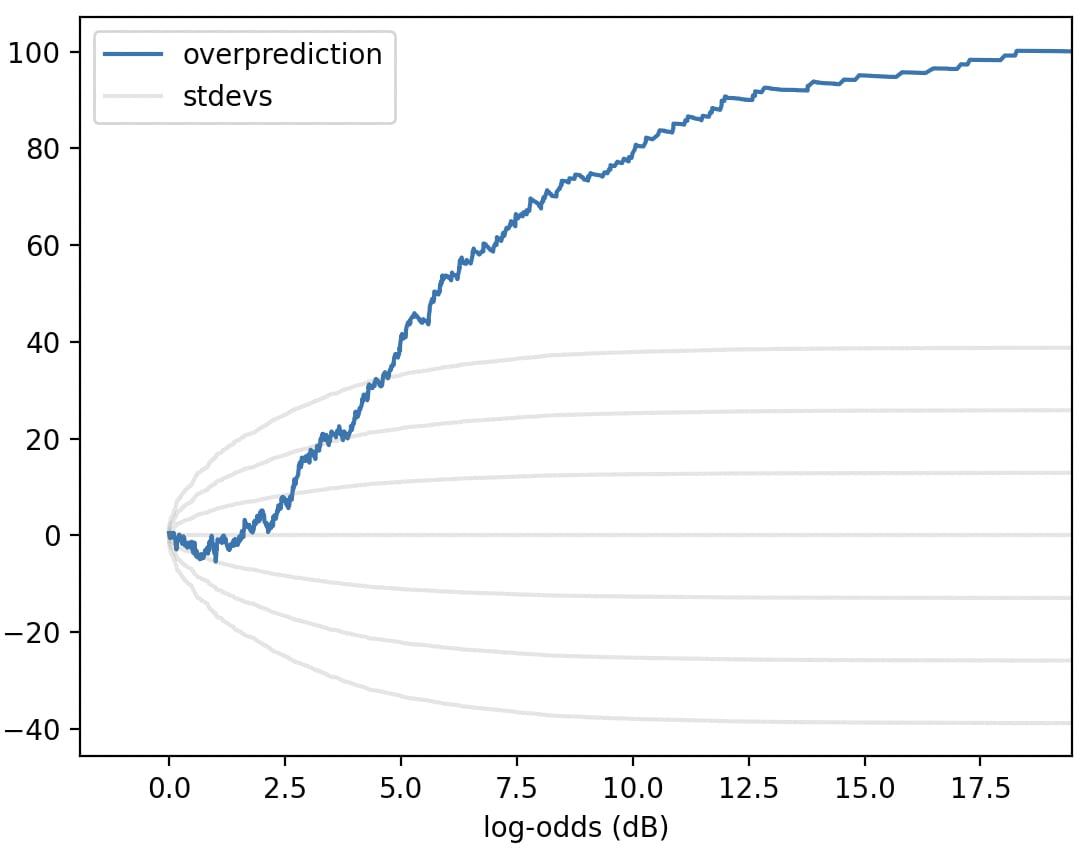
(same predictions from my last graph, but reflected, and logitified)
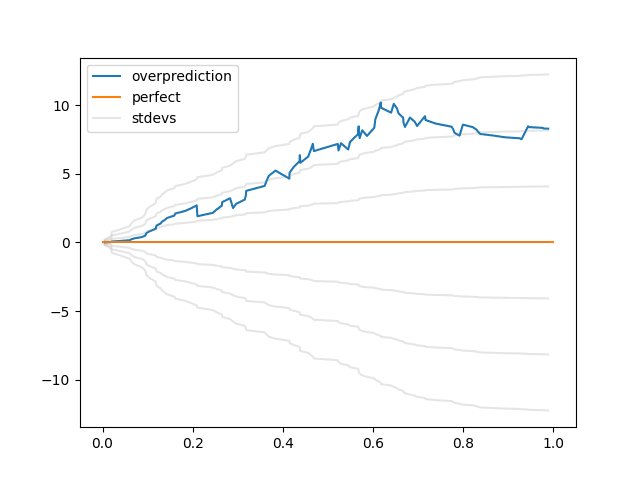
Hmm. This unflattering illuminates a deficiency of the "cumsum(prob - actual)" plot: in this plot, most of the rise happens in the 2-7dB range, not because that's where the predictor is most overconfident, but because that's where most of the predictions are. A problem that a normal calibration plot wouldn't share!
(A somewhat sloppy normal calibration plot for those predictions:
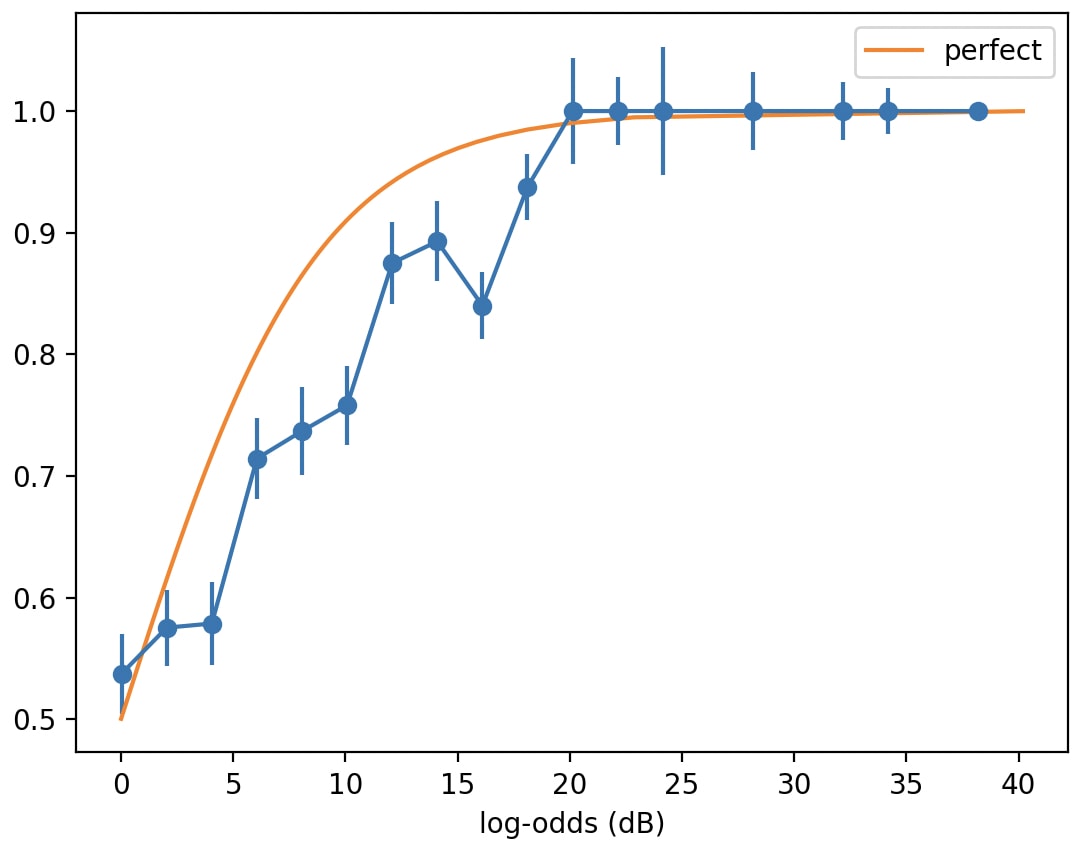
Perhaps the y-axis should be be in logits too; but I wasn't willing to figure out how to twiddle the error bars and deal with buckets where all/none of the predictions came true.)
I think something's off in the log-odds plot here? It shouldn't be bounded below by 0, log-odds go from -inf to +inf.
Ah-- I took every prediction with p<0.50 and flipped 'em, so that every prediction had p>=0.50, since I liked the suggestion "to represent the symmetry of predicting likely things will happen vs unlikely things won't."
Thanks for the close attention!
(Hmm. Come to think of it, if the y-axis were in logits, the error bars might be ill-defined, since "all the predictions come true" would correspond to +inf logits.)
forall p from 0 to 1, E[ Loss(p-hat(Y | X),p*(Y | X)) | X, p*(Y | X) = p]
p-hat is your predictor outputting a probability, p* is the true conditional distribution. It's expected loss for the predicted vs true probability for every X w/ a given true class probability given by p, plotted against p. Expected loss could be anything reasonable, e.g. absolute value difference, squared loss, whatever is appropriate for the end goal.
It sounds like you're assuming you have access to some "true" probability for each event; do I misunderstand? How would I determine the "true" probability of e.g. Harris winning the 2028 US presidency? Is it 0/1 depending on the ultimate outcome?
Curated and popular this week
