Intuitively, a function $f$ is a procedure (or machine) that takes an input and performs some operations to produce an output. For example, the function "+" takes a pair of numbers as input and produces their sum as output: on input (3, 6) it produces 9 as output, on input (2, 18) it produces 20 as output, and so on.

Formally, in mathematics, a function $f$ is a relationship between a set $X$ of inputs and a set $Y$ of outputs, which relates each input to exactly one output. For example, $-$ is a function that relates the pair $(4,3)$ to $1,$ and $(19,2)$ to $17,$ and so on. In this case, the input set is all possible pairs of numbers, and the output set is numbers. We write $f:X\to Y$ (and say "$f$ has the type $X$ to $Y$") to denote that $f$ is some function that relates inputs from the set $X$ to outputs from the set $Y$. For example, $-:(N\times N)\to N,$ which is read "subtraction is a function from natural number-pairs to natural numbers."

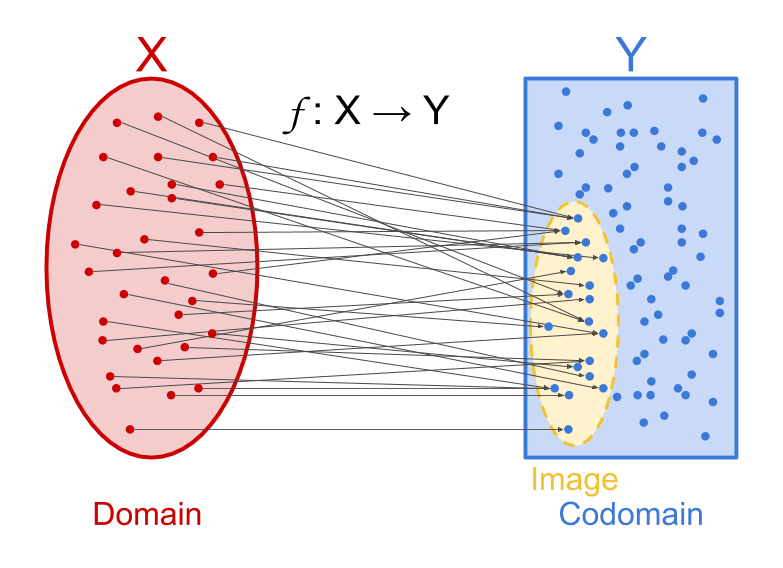
$X$ is called the domain of $f.$ $Y$ is called the codomain of $f$. We can visualize a function as a mapping between domain and codomain that takes every element of the domain to exactly one element of the codomain, as in the image below.

Examples

There is a function $f:R\to R$ from the real numbers to the real numbers which sends every real number to its square; symbolically, we can write $f\left(x\right)=x^2$.

(TODO)