As with the CCS post, I'm reviewing both the paper and the post, though the majority of the review is on the paper. Writing this quickly (total time on review: ~1.5h), but I expect to be willing to defend the points being made --
There's a lot of reasons I like the work. It's an example of:
- Actually poking inside a real model. A lot of the mech interp work in early-mid 2022 was focused on getting a deep understanding of toy models trained on algorithmic tasks (at least in this community).[1] There was some effort at Redwood to do neuron-by-neuron replacement, and Nix completed his work on the parentheses balancer concurrently to the IOI results, but insofar as there was mech interp work being done, most of it was on simple models such as the ones featured in Toy Models of Superposition or Modular Arithmetic Grokking (with the primary exception being the Induction Head results from Anthropic, which are substantively weaker outside of very small transformers).
This work was one of the first attempts to explain a particular, nontrivial behavior inside of a small but real LM (GPT-2-small). - Demonstrating the feasibility of patching and circuit-based analysis on language models. I think it's notable that this work doesn't just mechanistically study behavior inside of a language model, it finds a circuit (a small subgraph) implementing the behavior. This is valuable both as a confirmation that patching could be used to find circuits in "real" models, but also as evidence that we can find these circuits at all. In turn, this has led to a veritable explosion of "poking LLMs with various kinds of patching/scrubbing to identify subgraphs of particular behaviors", which I think has been pretty valuable on net.
Also, as Neel says below, it's important for pedagogical reasons. - Field-building via example. As with the Modular Arithmetic work by Neel, this was published in ICLR '23 as the joint first mech interp work to be published in a top conference. This helped build a substantial amount of legitimacy and academic interest for the field of mech interp (and broadly, ai x-risk flavored interp in general).
- Demonstrating failure modes and limitations of mech interp techniques. As stated in this post, an earlier version of this work used mean ablation in a way that preserved "information that helped compute the task", which incorrectly suggested that parts of the circuit were unimportant for performance. It's a concrete example of why important to think about what exactly you're ablating, and how your ablation serves as a valid test of your hypothesis.
This work also directly inspired Causal Scrubbing , which was an attempt to more completely remove information that helps complete a task. - Validating interp via adversarial inputs. I appreciate the use of adversarial example discovery as a downstream use case of the interp.
But there's also some reservations I have:
- Some of the presentation was misleading. Originally, the paper defined the IOI task as something along the lines of:
'... sentences like “When John and Mary went to the store, John gave a drink to” should be completed with “Mary”.'
That is, it did not make it clear that IOI was about assigning a higher logit to "Mary" than to "John", and not about assigning an (absolutely) high logit to "Mary". IIRC, this was only clarified near the end thanks to the effort of one of the critical ICLR reviewers.[2] There were also other strong claims that were significantly ameliorated by the ICLR review process.[3] - The circuit is likely overfit to the metric. I think that the mean logit difference is indeed the correct metric to look at, both because of how the task was defined and also for many use cases in general.[4] However, it's worth noting that this circuit does not hold up well if we replace the mean logit difference with other superficially similar metrics. E.g. if you replace the metric with mean absolute logit difference (i.e. E[|logit diff_model - logit diff_subgraph|]).
- The circuit is likely incomplete. Running Causal Scrubbing on the hypothesis suggests that it is importantly incomplete, see for example Alexandre's comment below. The incompleteness of the circuit also suggests some limitations of node-based causal interventions (i.e. activation patching in this case), as previously discussed. That being said, this wasn't something that could've really been known when the experiments were being done for this paper, as Causal Scrubbing was inspired by these results (and thus could not have been used to generate them).
And there's two big points that I'm very, very torn on (it's less to do with the work itself than general approaches to/issues with mech interp):
- Using an algorithmic task (IOI). As this post says, it's an example of "streetlight interpretability" -- looking where at cases that are easy, as opposed to where it's useful or realistic. I think it's valuable to do some amount of streetlight interpretability, and it's especially understandable in the case of this work (as one of the earliest mech interp pieces) but I do think that this is a weakness of the work. I also think that fact that seminal works in mech interp used algorithmic tasks may have contributed to a lack of attention paid to soft heuristics/memorization/n-gram statistic-style behavior inside of models, which I think are quite neglected.
- Low percent performance recovered. While the headline numbers for completeness/faithfulness are pretty high in terms of percentage, this actually is quite bad in terms of downstream performance.This isn't specific to this work. But, to use causal scrubbing as an example, if random performance on a task is 10 nats of log loss and the model's performance is 2.1 nats, recovering up to 2.6 nats might give the impressive number of 93.7% loss recovered. But in practice, 2.6 nats might be the performance of a model 1/100 or 1/1000 the size of the model we're trying to explain. If the behavior you're trying to explain is present in the most capable models but not in models a generation or two back, this work does not provide significant evidence that it's possible. Again, this isn't specific to this work, but to circuit-style mech interp on real models in general.
I think the post itself is pretty good though not exceptional -- I appreciate the explanation of how the task and approach were chosen, as well as the key takeaway that causal interventions can be powerful for mech interp, if they are performed appropriately, but doing them appropriately is challenging.
All said, I'm giving this a 4 on the annual review.
- ^
Note that there was plenty of non-mechanistic interp work that looked at real models and tasks; in fact, the majority of interp has always been on non-toy models and tasks. But mech interp was focused on toy tasks.
- ^
I helped out with rebuttals on this paper, and was honestly impressed by the two critical reviews posted by reviewer jy1a (official review, response to author rebuttal), who among (imo correct) issues correctly pointed out that the post was using this incorrect definition of IOI. Notice also how in the rebuttal response, they also point out the issue of using mean logit difference versus mean absolute logit difference. I think that (alongisde the RR AT paper) this was one of the reasons I updated to be more in favor of the existing academic peer review system.
- ^
See e.g. this comment from the Program Chairs:
The major concerns from the reviewers are the current limited limitation section and a few not-well supported/overstated claims in the paper. Request to the authors: Please update the paper to have a stronger and more critical limitation discussion, as well as substantially change the writing to justify all claims/assumptions (or not to overstate claims) in order to reflect reviewers’ comments.
- ^
The main reason is that we don't really care about 'noise' when explaining good performance, e.g. from the Causal Scrubbing appendix:
Suppose that one of the drivers of the model’s behavior is noise: trying to capture the full distribution would require us to explain what causes the noise. For example, you’d have to explain the behavior of a randomly initialized model despite the model doing ‘nothing interesting’.
That being said, this claim depends greatly on the implied downstream use case of interp. E.g. if the goal is to understand failure modes, then explaining just the success is insufficient.
I recently applied causal scrubbing to test the hypothesis outlined in the paper (as part of my work at Redwood Research). The hypothesis was defined from the circuit presented in Figure 2. I used a simple setting similar to the experiments on Induction Heads. I used two types of inputs:
- the correct input for the circuit.
- , an input with the same template but a randomized subject and indirect object. Used as input for the path not included in the circuit.
Results
Experiment 1
I allowed all MLPs on every path of the circuit. The only attention heads non-scrubbed in this hypothesis are the ones from the circuit, split by key, queries, values, and position as in the circuit diagram.
This experiment is directly addressing our claim in the paper, as we did not study MLPs (i.e. they are always acting as black boxes in our experiments).
The logit difference of the scrubbed model is 1.854±2.127 (mean±std), 50%±57 of the original logit difference.
Experiment 2
I connected Name Movers’ keys and values to MLP0 at the IO and S1 positions. All the paths from embeddings to these MLP0 are allowed.
I allowed all the paths involving all attention heads and MLPs from the embeddings to
- The queries of S-Inhibition Heads at the END position.
- The queries of the Duplicate Token Heads and Induction Heads at the S2 position.
- The keys and values of the Duplicate Token Heads at the S1 and IO position.
- The value of Previous Token heads at the S1 and IO position.
Inside the circuit, only the direct interactions between heads are preserved.
The logit difference of the scrubbed model is 0.831±2.127 (22%±64 of the original logit difference).
Comments
- How to interpret these numbers? I don’t really know. My best guess is that the circuit we presented in the paper is one of the best small sets of paths to look at to describe how GPT-2 small achieves high logit difference on IOI. However, in absolute, many more paths that we don't have a good way to describe succinctly matter.
- The measures are extremely noisy. This is consistent with the measure of logit difference on the original model, where the standard deviation was around 30% of the mean logit difference. However, I ran causal scrubbing on a dataset with big enough samples (N=100) that the numbers are interpretable. I don’t understand the source of this noise, but suspect it is caused by various names triggering various internal structures inside GPT-2 small.
- How does it compare to the validations from the paper? The closest validation score from the paper is the faithfulness score -- computing the logit difference of the model where all the nodes not in the circuit are mean ablated. In the paper, we present a score of 87% of the logit difference. I think the discrepancies with the causal scrubbing results from experiment 1 come from the fact that i) resampling ablation is more destructive than mean ablation in this case. ii) that causal scrubbing is stricter as it selects paths and not nodes (e.g. in the faithfulness tests, Name Mover Heads at the END position see the correct output of Induction Heads at the S2 position. This is not the case in causal scrubbing). The results of the causal scrubbing experiments update me toward thinking that our explanation is not as good as I thought from our faithfulness score, but not low enough to strongly question the claims from the paper.
Really excited to see this come out! This feels like one of my favourite interpretability papers in a while. The part of this paper I found most surprising/compelling was just seeing the repeated trend of "you do a natural thing, form a plausible hypothesis with some evidence. Then dig further, discover your hypothesis was flawed in a subtle way, but then patch things to be better". Eg, the backup name movers are fucking wild.
I really like this paper! This is one of my favourite interpretability papers of 2022, and has substantially influenced my research. I voted at 9 in the annual review. Specific things I like about it:
- It really started the "narrow distribution" focused interpretability, just examining models on sentences of the form "John and Mary went to the store, John gave a bag to" -> " Mary". IMO this is a promising alternative focus to the "understand what model components mean on the full data distribution" mindset, and worth some real investment in. Model components often do many things in different contexts (are polysemantic), and narrow distributions allow us to ignore their other roles.
- This is less ambitious and less useful than full distribution interp, but may be much easier, and still sufficient for useful applications of interp like debugging model failures (eg why does BingChat gaslight people) or creating adversarial examples.
- It really pushed forwards causal intervention based mech interp (ie activation patching), rather than "analysing weights based" mech interp. Causal interventions are inherently distribution dependent and in some sense less satisfying, but much more scalable, and an important tool in our toolkit. (eg they kinda just worked on Chinchilla 70B
- Patching was not original to IOI, but IOI is the first time I saw someone actually try to use it to uncover a circuit
- It was the first place I saw edge/path patching, which is a cool and important innovation on the technique. It's a lot easier to interpret a set of key nodes and how they connect up than just heads that matter in isolation.
- It's really useful to have an example of a concrete circuit when reasoning through mech interp! I often use IOI as a standard example when teaching or thinking through something
- When you go looking inside a model you see weird phenomena, which is valuable to know about in future - the role of the work is by giving existence proofs of these, so just a single example is sufficient
- It was the first place I saw the phenomena of backup/self-repair, which I found highly unexpected
- It was the first place I saw negative heads (which directly led to the copy suppression paper I supervised, one of my favourite interp papers of 2023!)
- It's led to a lot of follow-up works trying to uncover different circuits. I think this line of research is hitting diminishing returns, but I'd still love to eg have a zoo of at least 10 circuits in small to medium language models!
- This was the joint first mech interp work published at a top ML conference, which seems like solid field-building, with more than 100 citations in the past 14 months!
I personally didn't find the paper that easy to read, and tend to recommend people read other resources to understand the techniques used, and I'd guess it suffered somewhat from trying to conform to peer review. But idk, the above is just a lot of impressive things for a single paper!
An interesting aspect of the heuristic the model found is that it's wrong. That's why it's possible to construct adversarial examples that trick the heuristic.
I think if I'm going to accuse the model's heuristic of being "wrong" then it's only fair that I provide an alternative. Here's an attempt at explaining why "Mary" is the right answer to "When Mary and John went to the store, John gave a drink to":
- John probably gives the drink to one of the people in the context (John or Mary).
- If John were the receiver, we'd usually say "John gave himself a drink". (Probably not "John gave a drink to himself", and never "John gave a drink to John".)
- The only person left is Mary, so Mary is probably the receiver.
Instead the model "cheats" with a heuristic that might work quite often on the training set but doesn't properly understand what's going on, which makes it generalize poorly to adversarial examples.
I wonder whether this wrongness just reflects the smallness of GPT2-small, or whether it's found in larger models too. Do the larger models get better performance because they find correct heuristics instead, or because they develop a more diverse set of wrong heuristics?
Very interesting work! I have a couple questions.
1.
Looking at your example, “Then, David and Elizabeth were working at the school. Elizabeth had a good day. Elizabeth decided to give a bone to Elizabeth”. I'm confused. You say "duplicating the IO token in a distractor sentence", but I thought David would be the IO here?
I also tried this sentence in your tool and only got a 2.6% probability for the Elizabeth completion.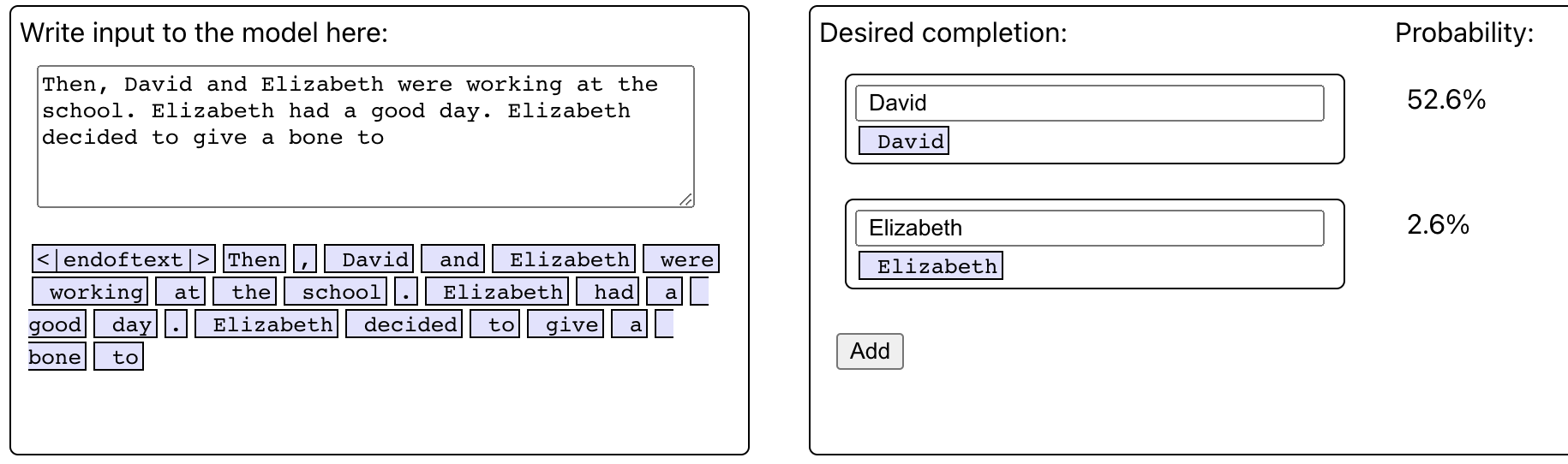
However, repeating the David token raises that to 8.1%.
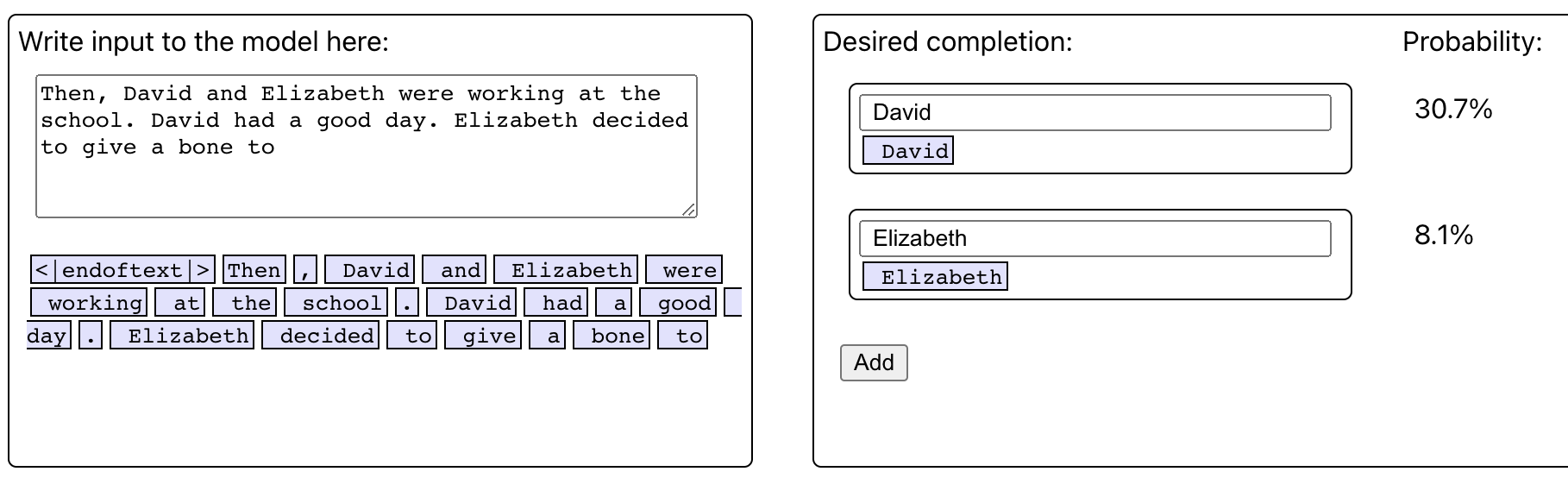
Am I confused about the meaning of the IO or was there just a typo in the example?
2.
In our work, it’s probably true that the circuits used for each template are actually subtly different in ways we don't understand. As evidence for this, the standard deviation of the logit difference is ~ 40% and we don't have good hypotheses to explain this variation. It is likely that the circuit that we found was just the circuit that was most active across this distribution.
I'd love if you could expand on this (maybe with an example). It sounds like you're implying that the circuit you found is not complete?
Thanks for your comment!
1.
Looking at your example, “Then, David and Elizabeth were working at the school. Elizabeth had a good day. Elizabeth decided to give a bone to Elizabeth”. I'm confused. You say "duplicating the IO token in a distractor sentence", but I thought David would be the IO here?
Am I confused about the meaning of the IO or was there just a typo in the example?
You are right, there is a typo here. The correct sentence is “Then, David and Elizabeth were working at the school. David had a good day. Elizabeth decided to give a bone to Elizabeth”
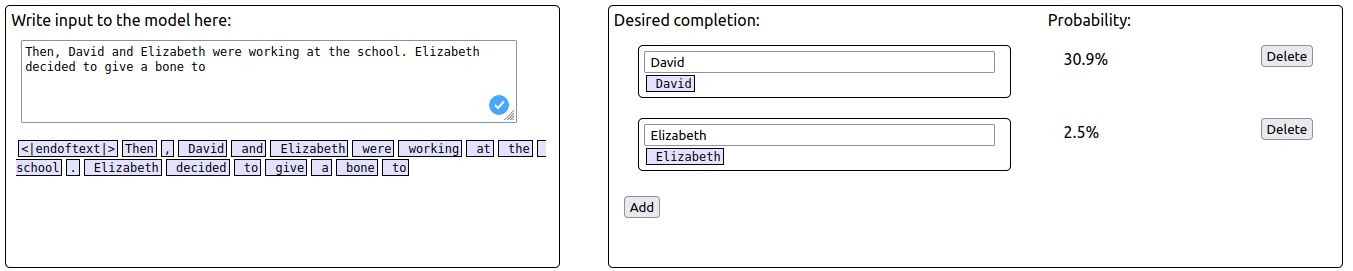
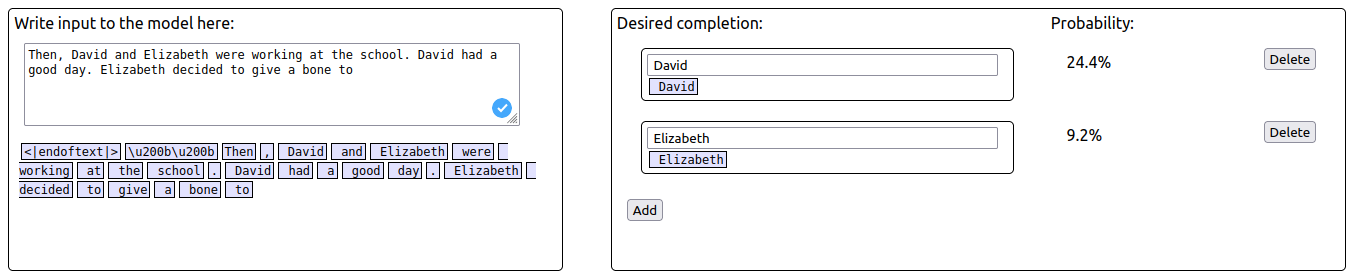
When using the corrected adversarial prompt, the probability of S ("Elizabeth") increases while the probability of IO ("David") decreases.
Thanks a lot for spotting the typo, we corrected the post!
2.
I'd love if you could expand on this (maybe with an example). It sounds like you're implying that the circuit you found is not complete?
A way we think the circuit can differ depending on examples is if there are different semantic meaning involved. For instance, in the example above, the object given is a "bone" such that a "a dog" could also be a plausible prediction. If "Elizabeth decided to give a kiss", then the name of a human seems more plausible. If this is the case, then there should be additional components interfering with the circuit we described to incorporate information about the meaning of the object.
In addition to semantic meaning, there could be different circuits for each template, different circuits could be used to handle different sentence structures.
In our study we did not investigate what differ between specific examples as we're always averaging experiments results on the full distribution. So in this way the circuit we found is not complete, as we can not explain the full distribution of the model outputs. However, we would expect that each circuit would be a variation of the circuit we described in the paper.
There are other ways we think our circuit is not complete, see the section 4.1 for more experiments on these issues.
Exciting work! A minor question about the paper:
Does this mean that it writes a projection of S1's positional embedding to S2's residual stream? Or is it meant to say "writing to the position [residual stream] of [S2]"? Or something else?
Thanks for the feedback!
Does this mean that it writes a projection of S1's positional embedding to S2's residual stream? Or is it meant to say "writing to the position [residual stream] of [S2]"? Or something else?
Our current hypothesis is that they write some information about S1's position (that we called the "position signal", not as straightforward as a projection of its positional embedding) in the residual stream of S2. (See the paragraph "Locating the position signal." in section 3.3). I hope this answer your questions.
We currently think that the position signal is a relative pointer from S2 to S1, computed by the difference between the positions S2 and S1. However, our evidence for this claim is quite small (see the last paragraph of Appendix A).
That's definitely an exciting direction for future research!
To learn more about this work, check out the paper. We assume general familiarity with transformer circuits.
Intro:
There isn’t much interpretability work that explains end-to-end how a model is able to do some task (except for toy models). In this work, we make progress towards this goal by understanding some of the structure of GPT-2 small “in the wild” by studying how it computes a simple natural language task.
The task we investigate is what we call indirect object identification (IOI), where sentences like “When John and Mary went to the store, John gave a drink to” should be completed with “Mary” as opposed to “John”.
We discovered the structure of a circuit of 26 attention heads grouped into 7 main classes, the largest end-to-end attempt to reverse engineer how a LM computes a natural behavior (to our knowledge). There is still much missing from our explanation, however, and our explanation doesn’t go to the parameter level.
Besides discovering the particular circuit shown above, we gained some interesting insights about low-level phenomena arising inside language models. For example, we found attention heads communicating with pointers (sharing the location of a piece of information instead of copying it). We also identified heads compensating for the loss of function of other heads, and heads contributing negatively to the correct next-token prediction. We're excited to see if these discoveries generalize beyond our case study.
Since explanations of model behavior can be confused or non-rigorous, we used our knowledge to design adversarial examples. Moreover, we formulate 3 quantitative criteria to test the validity of our circuit. These criteria partially validate our circuit but indicate that there are still gaps in our understanding.
This post is a companion post to our paper where we share lessons that we learned from doing this work and describe some of Redwood’s interpretability perspectives. We share high-level takeaways and give specific examples from the work to illustrate them.
Goals of Interpretability for this Investigation
In this kind of mechanistic interpretability work, we tend to use the circuits abstraction. If we think of a model as a computational graph where nodes are terms in its forward pass (neurons, attention heads, etc) and edges are the interactions between those terms (residual connections, attention, etc), a circuit is a subgraph of the model responsible for some behavior.
Note that our work is slightly different from Chris Olah's/Anthropic’s idea of a circuit in that we investigate this circuit on a specific distribution (instead of the entire distribution of text) and we also don’t attain an understanding of the circuit at the parameter-level.
Structure: Having all the nodes and edges
One kind of valuable interpretability insight is to ensure that we have the correct subgraph, which is one of the main goals in this work.
We formulate three main quantitative criteria to measure progress towards this goal. These criteria rely on the idea of "knocking out" or turning off a node from the computational graph by replacing its activation by its mean on a distribution where the IOI task is not present. (Note that we now believe that our causal scrubbing algorithm provides a more robust way to validate circuits.)
One particularly challenging task to meet these criteria is to understand distributed behaviors: behaviors where many components each contributes a little to compute some behavior in aggregate. We faced such a behavior when investigating the origin of the S-Inhibition Heads' attention patterns, one crucial class of heads in our circuit that bias the model output against the Subject token and towards the correct Indirect Object token. Unfortunately, we suspect that most LM behaviors consist of massive amounts of correlations/heuristics implemented in a distributed way.
Another important, though less challenging, task is to understand redundant behaviors: sometimes several model components appear to have identical behaviors when we study specific tasks. Our circuit is littered with redundant behaviors: all main classes of our circuit contain multiple attention heads.
Semantic Understanding: Understanding the information flow
Even if you identify a complete and minimal set of components important for a model behavior, you still might not actually understand what each component in the circuit does.
Thus, a first important goal of interpretability is to understand what semantic information is being moved from node to node.
One class of nodes whose semantic role we understand pretty robustly is the Name Mover Heads. Here, we are pretty confident that these attention heads copy name tokens. Specifically, we find that the OV circuit of these heads copies names, and that how strongly Name Mover Heads write a certain name into the residual stream is correlated with how much attention they pay to it.
Gaining this kind of semantic understanding is particularly difficult because the model’s internal representations are a) different from our own and b) different from the input embedding space. Being unable to tie model representations with facts about the input makes any sort of understanding difficult. Causal interventions are nice because they localize aspects of the model and link them to specific facts about the input, furthering our understanding.
Our semantic knowledge of how the circuit performs IOI can be summarized in a simple algorithm. On the example sentence given in introduction “When John and Mary went to the store, John gave a drink to”
Adversarial Examples: Using your understanding to generate predictions
Understanding all the nodes, edges, and information they move around is valuable, but, at the end of the day, we want to use this understanding to do useful things. In the future, we hope that powerful enough interpretability will enable discovery of surprising behavior or adversarial examples, potentially helping us fix or modify model behavior. Thus, seeing if our understanding of the IOI circuit in GPT-2 small helps us generate adversarial examples or any engineering-relevant insights could be useful (as discussed here).
Indeed, we were able to find adversarial examples based on our understanding of the IOI circuit. For example, prompts that repeat the indirect object token (the name of the person that receive something, IO in short) sometimes cause the model to output the subject token (the name of the person giving something, S in short) instead of the correct IO token i.e. GPT-2 small generate completions like “Then, David and Elizabeth were working at the school. David had a good day. Elizabeth decided to give a bone to Elizabeth”[1]. Since the IOI circuit identifies IO by recognizing that it is the only non-duplicated name in the sentence, we can trick the circuit by also duplicating the IO token in a distractor sentence. This adversarial attack made the model predict S over IO 23.4% of the time (compared to 0.7% without distraction).
Ultimately, because of the simplicity of this task, these adversarial examples aren’t that mindblowing: we could have found them without the circuit but with more messing around. However, we’re pretty happy that our understanding of the circuit enables us to find them easily (one author spent 1h thinking about adversarial examples before finding these). Understanding these adversarial examples further would be valuable future work.
Lessons we learned:
Causal Interventions are extremely powerful
The easiest way to get human-understanding of model internals is to understand how they transform/move information about the input. For example, looking at attention patterns provided a lot of intuition for what the heads in our circuit were doing during initial work.
With the idea that we should try and base our understanding of model internals off the input, we can use carefully designed causal interventions to tie aspects of model internals to facts about the input. A powerful causal intervention technique is activation patching, where you replace the activation of a component with its activation on another input. In this work, we develop a more targeted type of activation patching, which we call path patching. Path patching helps us measure the direct effect of an attention head on the key, query or value of another head, removing the effect of intermediate attention heads. We use both extensively in our work.
For example, we have found initial evidence that the S-Inhibition Heads move positional information around (described in Appendix A of the paper). If you patch head outputs from prompts of the form ABBA (Then, John and Mary…. Mary…) to BABA (Then, Mary and John, Mary….) and vice versa, you cause a large drop in performance. Since the only information that changes is where the names are located, this result implies that the S-Inhibition Heads give positional clues to tell where the Name Movers should pay attention to.
Causal interventions can precisely investigate the importance of a particular path of information flow for a behavior in a model. Additionally, they can always be quantified with the same metric, enabling easy comparison (in this work, we always measure the difference between the S and IO logit).
Causal interventions like activation patching are particularly useful when interpreting algorithmic tasks with schema-like inputs. Algorithmic tasks have easy-to-generate distributions of inputs with well-defined model behavior, which enable clearer interpretations of causal interventions.
For example, in the IOI distribution of prompts, prompts look like“ Then, [A] and [B] went to the [PLACE]. [B] gave an [OBJECT] to” where there is a clear indirect object. We can also easily create another distribution of prompts, which we call the ABC distribution, that looks like “Then, [A] and [B] went to the [PLACE]. [C] gave an [OBJECT] to” where there is no single indirect object. Intuitively, replacing activations from the IOI distribution at key nodes with the activations from the ABC distribution should decrease the model’s probability of outputting a clear indirect object.
Knockouts and Patching are Tricky: Do You Have the Right Distribution?
However, patching from the right distribution is pretty tricky. When you replace the output of a node with certain activations (either in patching or knockouts), it’s important to think about what information is present in those replacement activations, why it’s useful for that information to be present, and what effect that information will have on the rest of the model’s behavior.
As an example, let’s focus on mean ablations (replacing the output of an element by its mean activation). In earlier versions of this work, when we mean-ablated everything but the circuit to measure faithfulness, completeness, and minimality, we would replace unimportant nodes with their mean on a specific template in the IOI distribution. We wanted to mean-ablate to remove the effect of a node while still not destroying model internals (See Knockout section in the paper for more information).
This decision ended up being particularly bad because the mean activation over the IOI distribution still contained information that helped compute the task. For example, the circuit we propose involves induction heads and duplicate token heads which function to detect the duplicated name. Despite this, we initially found that mean-ablating the induction and duplicate token heads had little effect. Indeed, even if their mean activation did not contain which name was duplicated, it still contained the fact that a name was duplicated. This means that the functionality of those heads was not hampered with this early version of knockouts.
How We Chose This Problem: Picking the Task is Important
We like to call this kind of interpretability work “streetlight interpretability.” In a sense, we’re under a streetlight, interpreting the behaviors which we’re aware of and can see clearly under the light, while being unaware of all the other behaviors that lurk in the night. We try to interpret tasks that we think we’ll succeed at interpreting, creating selection pressure for easy-to-interpret behaviors. The IOI task, as a behavior under the streetlight, is probably unrepresentative of how easy it is to do interpretability in general and is not representative of the set of model behaviors you might have wanted to understand.
Picking the task to interpret is a large part of this work. We picked the IOI task, in large part, because it’s a crisp, algorithmic task (and thus easier to interpret). We discuss why we chose this specific problem in the following subsections:
Why focus on a big(ger) model over a small model?
We wanted to focus on a bigger model to learn more about the difficulties of large models. We were particularly excited to see if we could find evidence that mechanistic interpretability of large language models wasn’t doomed.
Why focus on an actual language model (that contains other behaviors/distractions) vs a toy model (with no distractions)?
Both approaches have their advantages. Working on toy models is nice because it’s a lot easier, which enables more complete understanding. On the other hand, working on an actual language model is a lot harder, but you can be a bit more confident that lessons learned will generalize to bigger, more capable models.
Why focus on crisp, algorithmic tasks vs soft heuristics/bigrams?
Algorithmic tasks (like IOI) are easier to interpret than bigram-y, heuristic-y tasks. One way to think about this is that algorithmic tasks need to compute discrete steps, which are more likely to create circuit structures with discrete components.
Another way to think about this is that algorithmic tasks are more likely to be coherent i.e. a model behavior is largely produced by a single circuit instead of an ensemble of circuits. One reason picking a behavior (and representative distribution to study the behavior) is difficult is because you don't know whether the behavior is completed by the same circuit across the entire distribution.
In our work, it’s probably true that the circuits used for each template are actually subtly different in ways we don't understand. As evidence for this, the standard deviation of the logit difference is ~ 40% and we don't have good hypotheses to explain this variation. It is likely that the circuit that we found was just the circuit that was most active across this distribution.
Meta
Feedback
If you have feedback for this work, we’d love to hear it! Reach out to kevin@rdrws.com, alexandre@rdwrs.com, arthur@rdwrs.com if you have thoughts or comments you want to share.
How you can do this work
We’re far from understanding everything about IOI, and there are many more exciting interpretability tasks to do. For IOI specifically, there are many not-well-understood mechanisms, and investigating these mechanisms would definitely lead to some cool stuff. For example, our understanding of the MLPs, the attention patterns of the S-Inhibition Heads, Layer Norm, the IOI circuit in different and larger models, understanding the circuit on adversarial examples and legibility related things are all lacking.
Doing this kind of interpretability is easy with EasyTransformer, a transformer interpretability library made by Neel Nanda, which we’ve added some functionality to. Check out our GitHub repo and this Colab Notebook to reproduce some of our key results.
We are looking for more algorithmic tasks that GPT-2 small can do to do interpretability on! Check out this post on our criteria for desirable behaviors from GPT-2 and the web tool for playing with the model.
If you want to do this kind of research, Redwood is running an interpretability sprint, which we’re calling REMIX (Redwood Research Mechanistic Interpretability Experiment) in January. Learn more about REMIX here.
Since our sentence were generated by randomly sampling places and objects to fill templates, the result can be quite silly sometimes.