Overview:

First, I show that there is only a moderate variation in the magnitude of the positional embeddings of GPT-2 past the initial 100 tokens.

Then I discuss how this magnitude stability is potentially useful for models to mitigate the effects of LayerNorm.

Modern models don't use additive positional embeddings, but the same incentives apply to keeping the norms of any potential Emergent Positional Embeddings stable.

Norms of Positional embeddings:

For the overall shape of the positional embeddings, see GPT-2's positional embedding matrix is a helix.

The plots below show the norms of the positional embeddings across 3 GPT-2 models, where you can see there is significant stability:

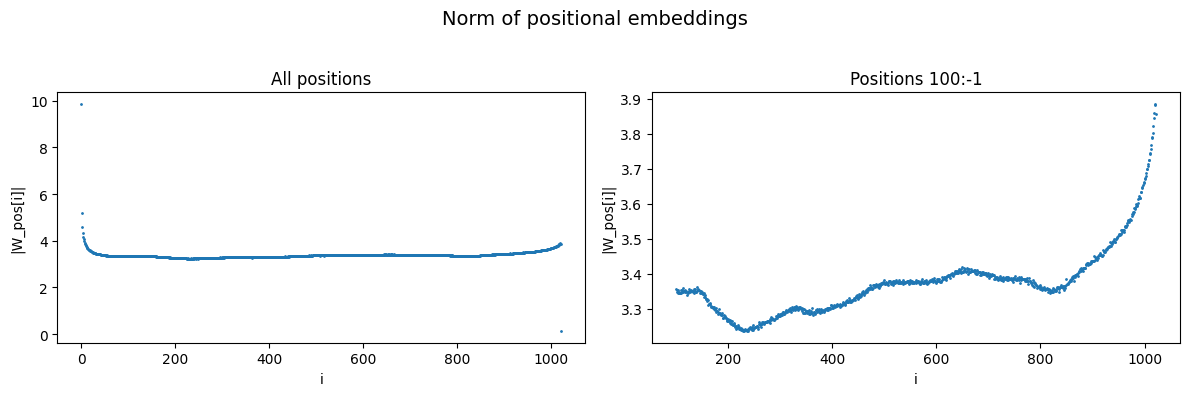
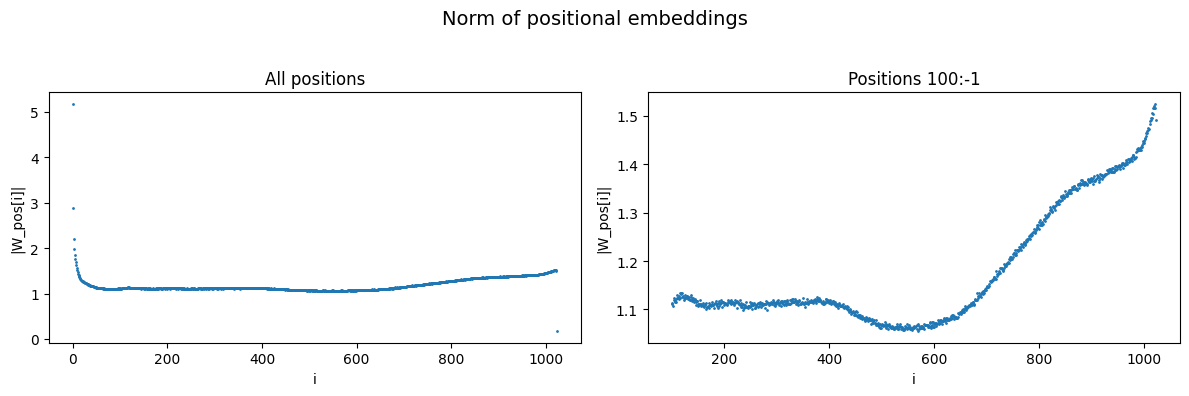
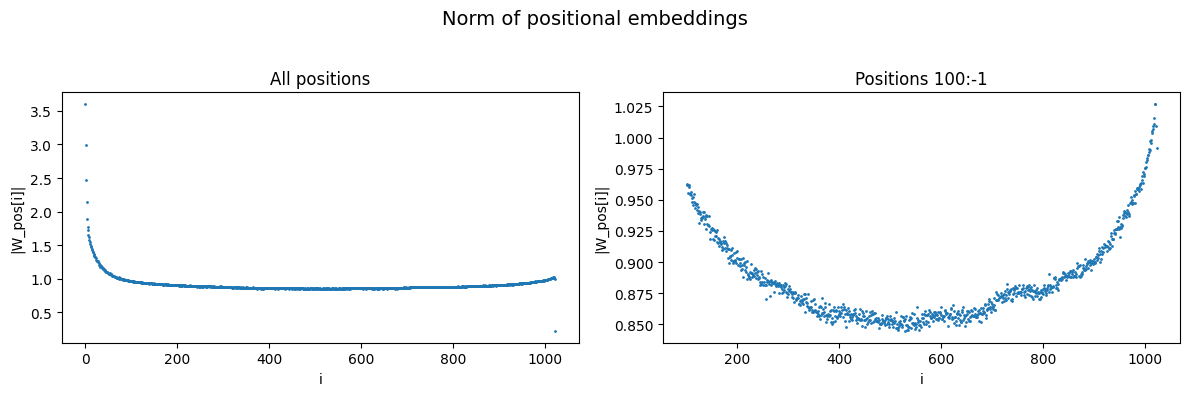
Why this is helpful for models/interpretability:

After folding in constants appropriately, the post LayerNorm input to the attention layer of a token $t$ at position $i$ is given by $\frac{W_E\left[t\right]+W_{\text{pos}}\left[i\right]}{|W_E\left[t\right]+W_{\text{pos}}\left[i\right]|}$. 

Ignoring the positional component, the token-dependent component is given by $\frac{W_E\left[t\right]}{|W_E\left[t\right]+W_{\text{pos}}\left[i\right]|}$. So the position $i$ is entangled with the token $t$ in a non-linear way, which makes it potentially difficult to reason about how the model will behave.

Fortunately, token embeddings are almost orthogonal to positional embeddings (maximum cosine sim of 0.15, and that's on a glitch token). Approximating them as exactly orthogonal, we get $|W_E\left[t\right]+W_{\text{pos}}\left[i\right]|\approx \sqrt{|W_E\left[t\right]{|}^2+|W_{\text{pos}}\left[i\right]{|}^2}\approx \sqrt{|W_E\left[t\right]{|}^2+C^2}$.

Where we approximate $|W_{\text{pos}}\left[i\right]|$ with a constant $C$, removing the $i$ dependence.

So by keeping the magnitude of the positional embeddings close to constant, the model can mitigate the entanglement of content and position caused by LayerNorm.

Emergent Positional Embeddings:

The same incentives to avoid the entanglement of content and position apply to any potential Emergent Positional Embeddings. If a model has an embedding of the sentence number (say for tasks like attending only to the current sentence), then we would expect these embeddings to also lie close to a hypersphere. 

We might have multiple emergent positional embeddings, for example:

$\text{total\_emb}=\text{content\_emb}+\text{pos\_emb}+\text{sentence\_emb}+\text{paragraph\_emb}$

Then if all the emergent positional embeddings are mutually orthogonal, and lie on their own hyperspheres, we have:

$|\text{total\_embedding}|\approx \surd (|\text{content\_emb}|²+C_1²+C_2²+C_3²)$

So that the interference between the emergent embeddings due to LayerNorm would be significantly mitigated.