This is a linkpost for https://www.openphilanthropy.org/blog/how-feasible-long-range-forecasting
Lukeprog posted this today on the blog at OpenPhil. I've quoted the opening section, and footnote 17 which has an interesting graph I haven't seen before.
How accurate do long-range (≥10yr) forecasts tend to be, and how much should we rely on them?
As an initial exploration of this question, I sought to study the track record of long-range forecasting exercises from the past. Unfortunately, my key finding so far is that it is difficult to learn much of value from those exercises, for the following reasons:
- Long-range forecasts are often stated too imprecisely to be judged for accuracy.
- Even if a forecast is stated precisely, it might be difficult to find the information needed to check the forecast for accuracy.
- Degrees of confidence for long-range forecasts are rarely quantified.
- In most cases, no comparison to a “baseline method” or “null model” is possible, which makes it difficult to assess how easy or difficult the original forecasts were.
- Incentives for forecaster accuracy are usually unclear or weak.
- Very few studies have been designed so as to allow confident inference about which factors contributed to forecasting accuracy.
- It’s difficult to know how comparable past forecasting exercises are to the forecasting we do for grantmaking purposes, e.g. because the forecasts we make are of a different type, and because the forecasting training and methods we use are different.
Despite this, I think we can learn a little from GJP about the feasibility of long-range forecasting. Good Judgment Project’s Year 4 annual report to IARPA (unpublished), titled “Exploring the Optimal Forecasting Frontier,” examines forecasting accuracy as a function of forecasting horizon in this figure (reproduced with permission):
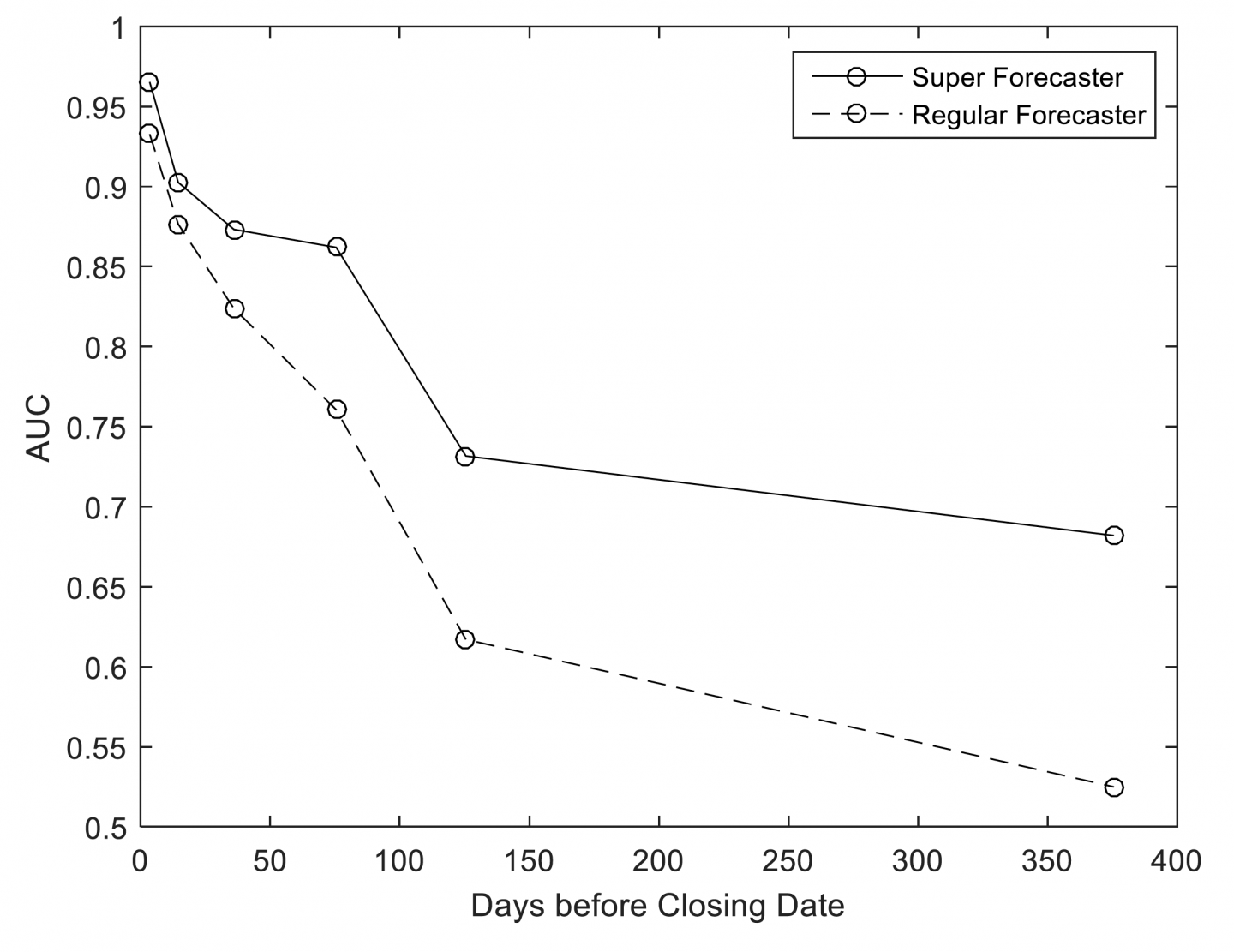
This chart uses an accuracy statistic known as AUC/ROC (see Steyvers et al. 2014) to represent the accuracy of binary, non-conditional forecasts, at different time horizons, throughout years 2-4 of GJP. Roughly speaking, this chart addresses the question: “At different forecasting horizons, how often (on average) were forecasters on ‘the right side of maybe’ (i.e. above 50% confidence in the binary option that turned out to be correct), where 0.5 represents ‘no better than chance’ and 1 represents ‘always on the right side of maybe’?”
For our purposes here, the key results shown above are, roughly speaking, that (1) regular forecasters did approximately no better than chance on this metric at ~375 days before each question closed, (2) superforecasters did substantially better than chance on this metric at ~375 days before each question closed, (3) both regular forecasters and superforecasters were almost always “on the right side of maybe” immediately before each question closed, and (4) superforecasters were roughly as accurate on this metric at ~125 days before each question closed as they were at ~375 days before each question closed.
If GJP had involved questions with substantially longer time horizons, how quickly would superforecaster accuracy declined with longer time horizons? We can’t know, but an extrapolation of the results above is at least compatible with an answer of “fairly slowly.”
I'd be interested to hear others' thoughts on the general question, and any opinions on the linked piece.