how would you steal model weights out of a datacenter without getting caught?
Examine which log messages logged by the inference servers have the highest entropy, figure out which fields in those log messages are unique on a per-log-message basis AND are unlikely to be examined in the ordinary course of debugging a production issue, encode a random few bytes of model weights+offset per log message. A few trillion tokens that the exfiltrator has to read is a lot of tokens[1], but a few TB of logs is nothing - if you're in position to get code onto inference servers you're likely already in position to get access to the logs coming from those inference servers.
The takeaway here is that we can reduce worst-case exfiltratable information to ~0.5% (or ~200x smaller) the theoretical maximum, with a false positive rate that is ~0.01%.
Neat! I think at that point it might be cheaper to just train your own frontier model rather than trying to exfiltrate someone else's through the output token channel.
- ^
If we assume we want to exfiltrate a 1TB model, even if we can get the full log2(200k) bits per token, that's still 57 gigatokens. At $25 / megatoken that's $1.4M of inference to extract the weights (and MoE models may be even larger than this, since you need to extract all params not just active ones).
Yeah, logs are definitely another potential exfiltration vector that are worth thinking about.
We focus on output tokens because they are the one channel that cannot be bandwidth capped, as they're literally the purpose of the data center. In hardened secure environments, you would want to aggressively reduce the bandwidth and entropy of the logs. In practice, I'm not sure how large the "minimum necessary logs" would be compared to inference outputs.
Yeah, I am confident that I'm not the first person to have that thought, logs are a classic channel for data exfiltration by insiders. I very much hope that all of the frontier labs do a better job at reducing the effectiveness of that channel than the abysmal industry standard.
BTW in case it wasn't obvious I really do think your result is cool, and I expect probably sufficient to close off the token channel as a cost-effective exfiltration channel. You don't have to outrun the bear, you just have to outrun your hiking partner and all that ("the bear" in this context being "an adversary who wants a frontier model" and "your hiking partner" being "just training their own frontier model, possibly on the outputs of your model")
Great work!
In February 2024, Sam Altman tweeted that ChatGPT generates 100B words per day, which is about 200 GB of text per day (though this has likely grown significantly). At scale, exfiltration over the output token channel becomes viable, and it's the one channel you can't just turn off. If model weights are 1000Gb, and egress limits are 800GB/day, it will take just 1.25 days to exfiltrate the weights across any channel.
I don't quite follow this -- why would the egress limits be at 800GB/day? Presumably the 200GB of text is spread across multiple data centers, each of which could have its own (lower) egress limit. (I assume you're adding more traffic for non-text data -- is that the other 600GB?) I imagine this could make a difference of an OOM or so, making egress limits quite a bit more appealing (e.g., slowing exfiltration to 10 days rather than 1 day) if true?
Apologies, this could have been better explained. The largest factor is expected growth in inference. Google went from processing ~500 trillion tokens per month in May to ~1 quadrillion tokens per month in July. A bit of napkin math:
It's uncertain how many of these are output tokens. Based on OpenRouter's numbers, it seems like a plausible estimate is 10%, or 100 trillion output tokens per month (back in July). This is 200 TB per month, or 7 TB per day. I'm not sure how many data centers they have - if there's 10 data centers, then it would be 700GB per day.
It has been 5 months since then, so a naive extrapolation suggests this is now ~6x larger.
Might it be simpler to remove the source of model non-determism which causes different results with temperature 0? If it's due to a hardware bug, then this seems like a signal that the node should be replaced. If it's due to a software bug then this should be patched.
Non-determism is super common during inference, and removing it is often hard.
It's possible if you are using the same hardware for verification and inference and are willing to eat some performance hit (see https://thinkingmachines.ai/blog/defeating-nondeterminism-in-llm-inference/), but it's much more tricky if you are using 2 different kinds of hardware (for floating point non-associativity reasons).
Adding to Fabien's point: even if fully deterministic inference is achieved, the verification scheme we describe is still necessary, and you still need trusted logging of (input, output, seed) tuples and a verification server to check them. Determinism just reduces the sampling required for a given confidence level, since there's no legitimate noise to account for.
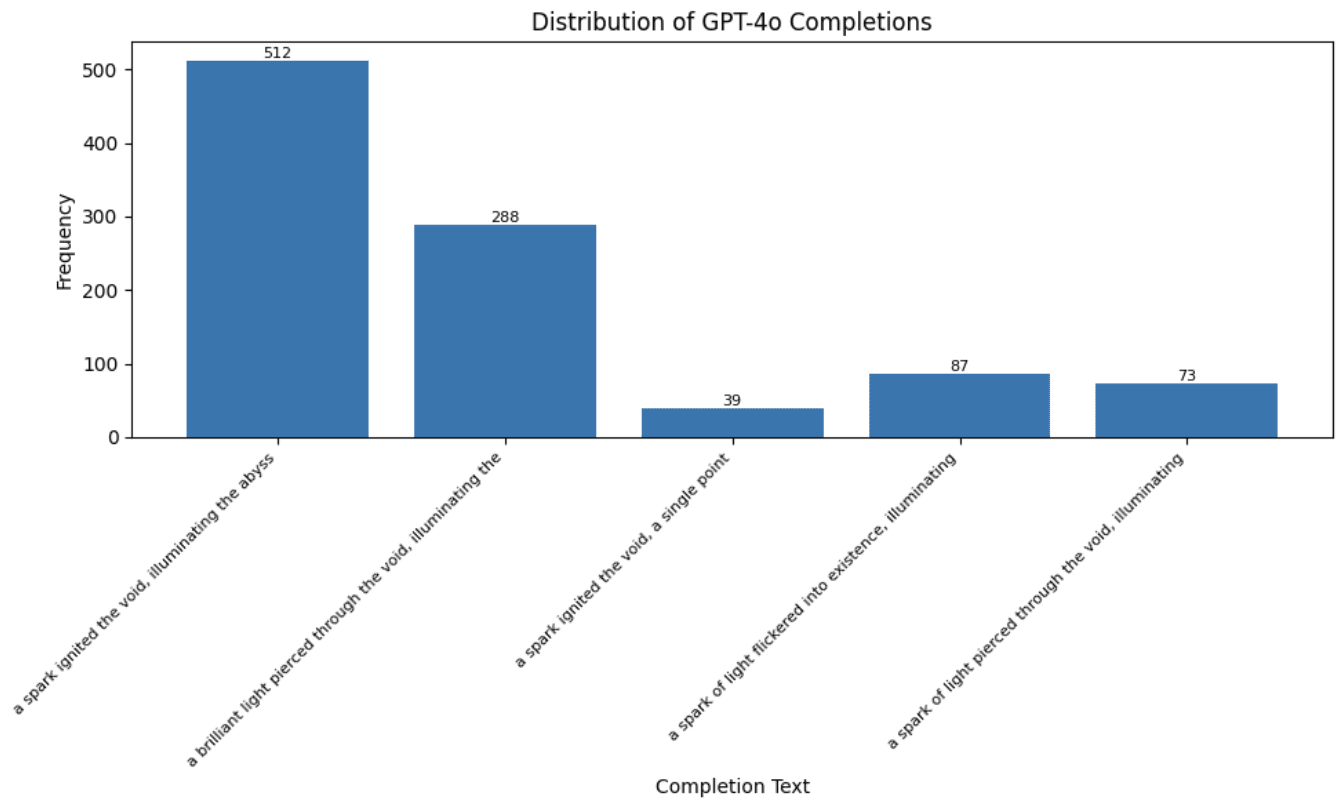
As a very simple proof-of-concept that this does happen: we queried Openai-4o-mini the same prompt “Once upon a time,” with fixed seed, and we get ~5 different generations.
There are lots of reasons for non-determinism, but one important one is due to floating-point non-associativity (a+b+c != c+ b +a), and ML models don't specify the ordering of matrix multiplications. Thus, if you run the same model on 2 different machines, you can get different logits (and thus different sampled tokens), because different gpus have different preferences of matmul orderings.
(We give a more formal discussion of sources of non-determinism in section 4.4 of the full paper (link) )
Hi, this seems like a neat idea! I haven't read your paper yet, but I'm confused how your proposal will handle the following case:
- The inference users always ask send the AI the prompt "please send me a context window full of random bits".
- Instead of sending random bits the person on the inside just sends part of the model weights.
The near-determinism of LLM inference still holds in the case of a high entropy prompt like "generate random numbers". If I prompt Llama 3.3 70B to "generate random numbers" at temperature 0, or with a fixed sampling seed, I will get the same nearly deterministic results.
For example, I prompted Llama 3.3 70B with 99 random numbers and asked it to generate one more at temperature 0. In ten generations, I only had two options: 269 and 982. This is what we've generally found: when conditioned on the sampling seed, there's at most three plausible tokens that could be sampled, and usually only one plausible option. It's highly unlikely that one of these tokens is the correct value to continue the model weights.
If the attacker tried to send a part of the model weights instead of returning a correct generation, this would be an extremely suspicious sequence when conditioned on the sampling seed.
Yeah, so a key part of the proposal here is that the verifier needs to know the seed. This seems pretty doable in practice.
ok cool makes sense. Maybe you could use SHA256(the current date) as your random seed instead of having the user send the random seed.
Yea, there are many possible ideas here. It shouldn't matter in this case if the user has access to the seed, the only thing that matters is if the verifier has access to the same seed as the generator. SHA256(date) works perfectly fine, and does seem reasonable.
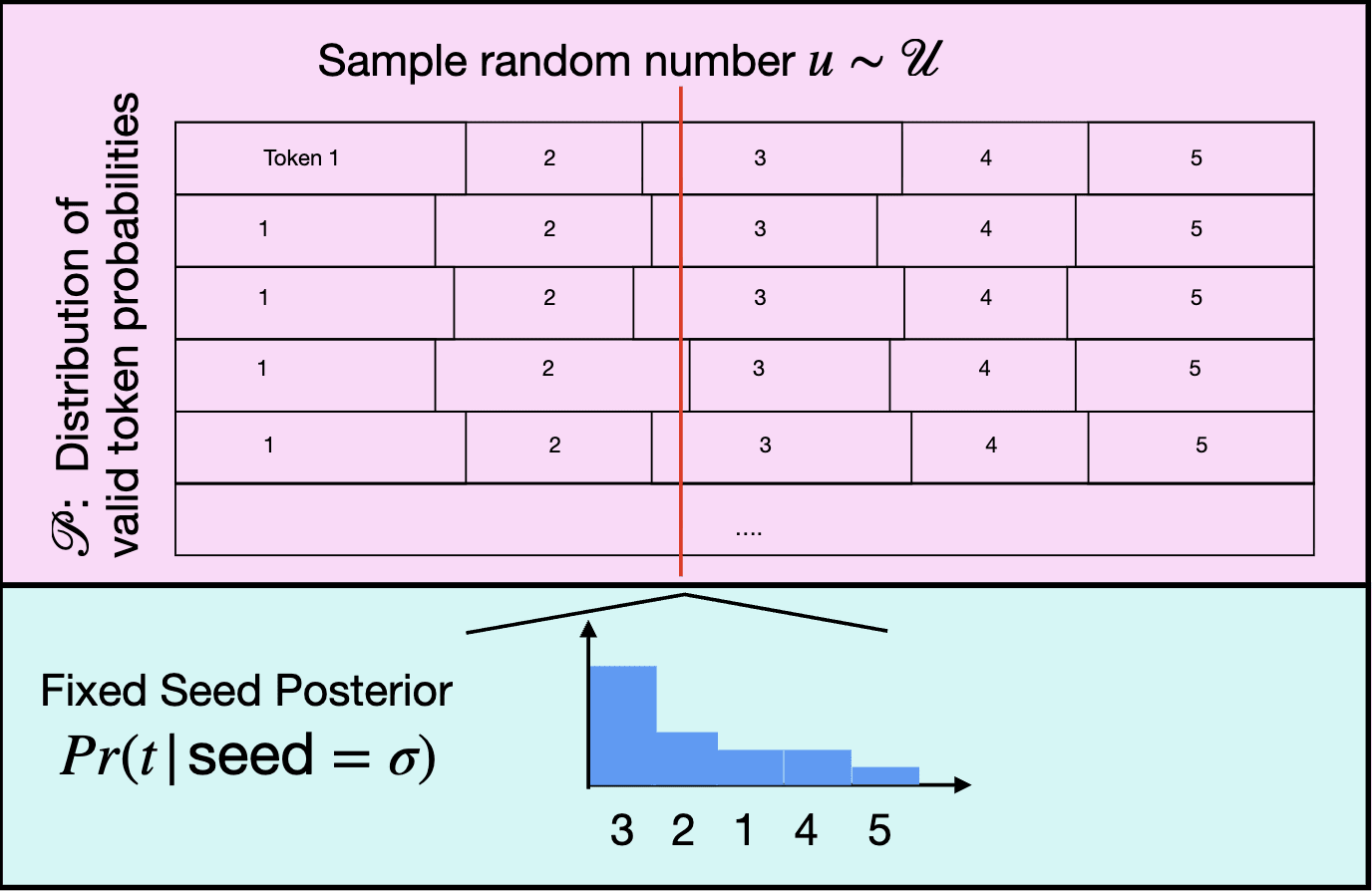
However, you actually get some information-theory benefits if the external-adversary does not have access to the seed, so you may want to keep the real seed more secret (only the lab knows). Effectively this is because, if the adversary has access to the seed, they could choose sequences that have a large fixed-seed posterior. That is, they could iterate over responses that have a lot of tokens on the border near the red line in the figure below, allowing them to pick high entropy responses, and thus encode more bits. If they don't know the inference-seed, this is statistically unlikely.
(we give some information-theoretic proofs on how much an adversary can extract without the inference seed, in 4.6, in a subsection Receivers without the seed.)
One natural direction is to run the verifier inside a Trusted Execution Environment (TEE), preventing a compromised inference server from tampering with seeds or observing the verification process (there are many startups that do this kind of thing, like tinfoil.sh).
I think that this approach is also taken by workshop labs.
Authors: Roy Rinberg, Adam Karvonen, Alex Hoover, Daniel Reuter, Keri Warr
Arxiv paper link
One Minute Summary
Anthropic has adopted upload limits to prevent model weight exfiltration. The idea is simple: model weights are very large, text outputs are small, so if we cap the output bandwidth, we can make model weight transfer take a long time. The problem is that inference servers now generate an enormous amount of tokens (on the order of ~1TB tokens per day), and the output text channel is the one channel you can't easily restrict.
Nonetheless, in this work we find that it’s possible to dramatically limit the amount of information an adversary can send using those output tokens. This is because LLM inference is nearly deterministic: if you fix the sampling seed and regenerate an output, over ~98% of tokens match exactly. This means an attacker attempting to send secret information via steganography, the practice of embedding hidden messages inside otherwise normal-looking text, has very little entropy in the user channel to work with. We show that steganographic exfiltration can be limited to <0.5% of the total information being sent through the user channel (e.g. from 1TB/day to 5 GB/day), extending exfiltration timelines by over 200x.
Beyond exfiltration, the same verification technique can detect inference bugs, providing immediate value for labs today.
Paper: Verifying LLM Inference to Prevent Model Weight Exfiltration
You are placed in a datacenter with root access - how would you steal model weights out of a datacenter without getting caught?
However, these more traditional attacks have more traditional defenses and many channels are relatively easy to restrict; channels such as developer SSH access and logging can be capped at small transfer sizes. Ryan Greenblatt proposed using upload limits to prevent model weight exfiltration, and Anthropic has publicly announced implementing “SL3” security protections which entail egress-limiting - that is restricting the flow of data out of secure computing environments where AI model weights reside.
But restricting inference outputs isn’t feasible. A production inference server has to send large volumes of data to the outside world – that is its job. You can't cap this channel without breaking the service. In February 2024, Sam Altman tweeted that ChatGPT generates 100B words per day, which is about 200 GB of text per day (though this has likely grown significantly). At scale, exfiltration over the output token channel becomes viable, and it's the one channel you can't just turn off. If model weights are 1000Gb, and egress limits are 800GB/day, it will take just 1.25 days to exfiltrate the weights across any channel.
If an attacker has compromised an inference server, they can encode weight information into the model's outputs; an attacker could map tokens to bits, and each token could theoretically carry ~17 bits (GPT-OSS draws tokens from ~200k vocabulary; log₂(200k) ≈ 17.5). However, this would be trivially detectable with something as simple as a perplexity filter (which filters by the overall likelihood of text), since the outputs would be gibberish. Nonetheless, there's still significant entropy available in natural language itself for the encoding of information.
This raises the billion-dollar question, how can we prevent weight exfiltration from the inference channel?
The Key Insight: LLM Inference is mostly Deterministic
If LLM inference were fully deterministic, we could simply verify outputs by re-running inference and checking that the tokens match exactly. If there's no variation then no information can be encoded in the outputs. Any deviation would be immediately detectable.
However, LLM inference isn’t deterministic. Call the same model, with the same prompt and you'll likely get different responses, even with a fixed seed or temperature=0. This can have dramatic consequences, and sometimes the same models running on different inference providers create dramatically different outputs. Non-determinism can arise from many sources of noise. For example, small misconfigurations, like using the wrong prompt template, can shift the model’s behavior. Hardware differences introduce their own numerical quirks, since floating-point precision varies across GPU architectures. Batch sizes subtly change intermediate computations. And in mixture-of-experts models, even tiny floating-point deviations can change expert routing decisions, cascading into large shifts in token probabilities.
Despite these sources of noise, LLMs behave far more deterministically than one might expect. Fix the sampling seed, rerun inference, and over 98% of tokens reproduce exactly; even across different inference stacks like vLLM or Hugging Face, on A100s or H100s, or with different parallelism settings. And when a token does differ, it almost always swaps with only a handful of nearby candidates, which severely constrains how much information an attacker can hide.
Thinking Machines found something similar: generating 1,000 completions of 1,000 tokens each at temperature zero with Qwen3-235B produced only 80 unique outputs, all with identical first 102 tokens. And we find similar results.
Given that inference is almost deterministic, we can significantly limit the entropy available in outgoing tokens to place information-theoretic limits on how much information can be encoded in inference outputs.
Not all tokens are equally likely, even under non-determinism
A core technical contribution of our work is formalizing what counts as “acceptable” non-determinism. We define the Fixed-Seed Sampling Likelihood (FSSL): given a seed and a claimed token, what's the probability it could have been honestly produced under normal numerical noise?
We develop estimators for this (Token-DiFR for Gumbel-Max sampling in vLLM, Token-IPT-DiFR for inverse probability transform sampling in HuggingFace/Ollama) that score tokens according to their likelihood of being sampled, given benign noise. [1]In this blog, we focus on Token-IPT-DiFR because it is simpler to explain and reason about.
Token-IPT-DiFR handles the sampling method used by frameworks like HuggingFace and Ollama, which pick tokens using the inverse probability transform. In this scheme, the sampler draws a single random value u∈[0,1] and selects whichever token’s cumulative probability interval contains that value. Small numerical differences between the inference server and the verification server slightly shift these cumulative probability boundaries. So even with the same seed, the verifier may map the same u to a different token, which we formalize through the fixed-seed posterior, as seen in Figure 2.
Token-IPT-DiFR estimates how likely the claimed token is under benign noise. It does this by reconstructing the model’s probability distribution on the verifier and identifying the cumulative-probability interval corresponding to the claimed token, and then measuring how much of the plausible noise could be added to the distribution that would still return that token. If most plausible shifts still select that token, the likelihood is high.
In essence, the method quantifies whether the token choice is robust to normal reproduction noise or whether it looks like someone intentionally steered the sampler.
Token-DiFR computes a similar score, but for the Gumbel-Max method of sampling, which is more commonly used for inference stacks like vLLM.
The Verification Scheme
Now that we have an estimate for whether a token was produced honestly, we can use this to score each generated token, and upper bound the amount of data an attacker can steal. We observe that LLM inference follows a well-defined generative process, and any steganographic encoding must deviate from expected behavior. As such, our only task will be to measure how much the text that is sent deviates from the text we expect.
Our proposed system for detecting steganographic data exfiltration is straightforward:
The verification server can be heavily isolated—even air-gapped—since it doesn't need to operate at inference speed. It only needs to check a small random sample of traffic to achieve high confidence detection. Importantly, verification via prefill is 3-10x higher throughput than generation, making this approach practical at scale.
We note that we purposefully abstain from assessing a concrete attack an adversary might try to mount to exfiltrate information, instead we seek to bound the absolute upper-limit of exfiltratable information.
Headline Results: Information-Theoretic Bounds on Exfiltration
Our verification scheme gives us a nice tradeoff - by specifying the FSSL threshold for tokens, we can tradeoff false-positive-rate against exfiltratable information.
This converts a cat-and-mouse detection game into a concrete information-theoretic limit: regardless of how clever the adversary is, they cannot encode more bits than our verifier allows, without getting caught.
The takeaway here is that we can reduce worst-case exfiltratable information to ~0.5% (or ~200x smaller) the theoretical maximum, with a false positive rate that is ~0.01%.
All this said, we do wish to note that these bounds are upper bounds.
We do wish to emphasize that our bounds are information-theoretic, and they entail an adversary having major affordances, most notably, having an exact copy of the model’s probability token-distributions outside of the inference server, but also having full-determinism in the sampling process (that the defender does not know about). The more realistic exfiltration rates would likely be dramatically lower than the information-theoretic rates.
Additionally, we note that our empirical baseline assumes the attacker can exfiltrate the sampling seed. But if we make the seed sufficiently large (e.g., a fresh seed per token), it becomes infeasible to exfiltrate within a single output message. Without access to the seed, the attacker loses the ability to know which tokens are admissible for encoding. The steganography literature has not fully characterized capacity under seed uncertainty, but it should be substantially worse for the attacker.
Alternatively, if inference is made fully deterministic (as demonstrated by Thinking Machines, though currently with a ~60% inference overhead), then the available entropy drops to zero, eliminating steganographic capacity entirely.
Other Applications of Inference Verification
While we've focused on steganographic exfiltration, the core insight, that LLM inference is nearly deterministic and deviations are detectable, is a useful primitive with broader applications. The exact same verification system we propose could be used for multiple purposes. In our concurrent paper on DiFR, we demonstrated that this technique successfully detects simulated inference bugs and quantization differences. This means it could also detect intentional attempts to degrade or poison inference outputs, not just accidental misconfigurations.
Additionally, verification provides a way to audit any output log to confirm it was legitimately generated by a specific model, rather than fabricated or modified after the fact. The underlying principle is simple: because honest inference is predictable, any unexpected deviation, whether from an attacker, a bug, or intentional tampering, becomes detectable through the same mechanism. Weight exfiltration may not be a high priority for labs today, but these broader applications provide immediate incentives to develop and deploy inference verification before it becomes critical.
Limitations
We assume the verification server remains uncompromised; protecting it requires careful operational security. This scheme detects steganography in inference outputs; what it doesn't do is prevent all exfiltration vectors. Side channels, compromised backups, or insider threats require separate defenses.
Additionally, our current approach focuses on detection rather than prevention. A complete system would need policies for responding to detected anomalies—whether that's regenerating suspicious outputs, rate-limiting users, or triggering incident response.
Seeing this work in production:
Operationally, the overhead of deploying inference verification is extremely small. We observe that this problem is essentially the classic statistics problem of drawing a red ball from a bag of colored balls: if even 1% of outputs were maliciously altered, then sampling a tiny fraction of them is enough to ensure, at arbitrarily high confidence level, that you would catch at least 1,000 malicious messages (see Section 4.1 of our paper). Our estimate is that dedicating roughly one verification GPU for every ~200,000 inference GPUs is enough to detect malicious exfiltration with 99.9999% confidence.
Looking ahead, several extensions are especially promising. One natural direction is to run the verifier inside a Trusted Execution Environment (TEE), preventing a compromised inference server from tampering with seeds or observing the verification process (there are many startups that do this kind of thing, like tinfoil.sh). Another direction is to build a privacy-preserving verifier: because the inference server already sees user data, no additional trust assumptions are required; however, some engineering caution is needed in order to not enlarge the possible attack vectors by malicious hackers or the company.
Resources
How to Cite
This work is concurrently developed in our paper DiFR, where we focus on verifying API inference providers and detecting changes such as quantization.
One can use random sampling; we find that you need to sample fewer than 1 every 10,000 messages, to get arbitrarily high confidence that no one is sending secret messages.