I think the smoking lesion problem is one of those intuition pumps that you have to be *very* careful with mathematizing and comparing with other things. Let me just quote myself from the past:
In the Smoking Lesion problem, and in similar cases where you consider an agent to have "urges" or "dispositions" et c., it's important to note that these are pre-mathematical descriptions of something we'd like our decision theory to consider, and that to try to directly apply them to a mathematical theory is to commit a sort of type error.
Specifically, a decision-making procedure that "has a disposition to smoke" is not FDT. It is some other decision theory that has the capability to operate in uncertainty about its own dispositions.
I think it's totally reasonable to say that we want to research decision theories that are capable of this, because this epistemic state of not being quite sure of your own mind is something humans have to deal with all the time. But one cannot start with a mathematically specified decision theory like proof-based UDT or causal-graph-based CDT and then ask "what it would do if it had the smoking lesion." It's a question that seems intuitively reasonable but, when made precise, is nonsense.
I think what this feels like to philosophers is giving the verbal concepts primacy over the math. (With positive associations to "concepts" and negative associations to "math" implied). But what it leads to in practice is people saying "but what about the tickle defense?" or "but what about different formulations of CDT" as if they were talking about different facets of unified concepts (the things that are supposed to have primacy), when these facets have totally distinct mathematizations.
At some point, if you know that a tree falling in the forest makes the air vibrate but doesn't lead to auditory experiences, it's time to stop worrying about whether it makes a sound.
So obviously I (and LW orthodoxy) are on the pro-math side, and I think most philosophers are on the pro-concepts side (I'd say "pro-essences," but that's a bit too on the nose). But, importantly, if we agree that this descriptive difference exists, then we can at least work to bridge it by being clear about whether were's using the math perspective or the concept perspective. Then we can keep different mathematizations strictly separate when using the math perspective, but work to amalgamate them when talking about concepts.
Oh, I more or less agree :P
If there was one criticism I'd like to repeat, it's that framing the smoking lesion problem in terms of clean decisions between counterfactuals is already missing something from the pre-mathematical description of the problem. The problem is interesting because we as humans sometimes have to worry that we're running on "corrupted hardware" - it seems to me that mathematization of this idea requires us to somehow mutilate the decision theories we're allowed to consider.
To look at this from another angle: I'm agreeing that the counterfactuals are "socio-linguistic conventions" - and I want to go even further and place the entire problem within a context that allows it to have lots of unique quirks depending on the ideas it's expressing, rather than having only the straightforward standardized interpretation. I see this as a feature, not a bug, and think that we can afford to be "greedy" in trying to hang on to the semantics of the problem statement rather than "lazy" in trying to come up with an efficient model.
Yeah, I agree that I haven't completely engaged with the issue of "corrupted hardware", but it seems like any attempt to do this would require so much interpretation that I wouldn't expect to obtain agreement over whether I had interpreted it correctly. In any case, my aim is purely to solve counterfactuals for non-corrupted agents, at least for now. But glad to see that someone agrees with me about socio-linguistic conventions :-)
Sure. I have this sort of instinctive mental pushback because I think of counterfactuals primarily as useful tools for a planning agent, but I'm assuming that you don't mean to deny this, and are just applying different emphasis.
Yeah, there's definitely a tension between being a social-linguistic construct and being pragmatically useful (such as what you might need for a planning agent). I don't completely know how to resolve this yet, but this post makes a start by noting that in additional to the social linguistic elements, the strength of the physical linkage between elements is important as well. My intuition is that there are a bunch of properties that make something more or less counterfactual and the social-linguistic conventions are about a) which of these properties are present when the problem is ambiguous b) which of these properties need to be satisfied before we accept a counterfactual as valid.
Still super confused why you are trying this convoluted and complicated approach, or mixing this problem with Newcomb's, while the useful calculation is very straightforward. To quote from my old post here:
An agent is debating whether or not to smoke. She knows that smoking is correlated with an invariably fatal variety of lung cancer, but the correlation is (in this imaginary world) entirely due to a common cause: an arterial lesion that causes those afflicted with it to love smoking and also (99% of the time) causes them to develop lung cancer. There is no direct causal link between smoking and lung cancer. Agents without this lesion contract lung cancer only 1% of the time, and an agent can neither directly observe, nor control whether she suffers from the lesion. The agent gains utility equivalent to $1,000 by smoking (regardless of whether she dies soon), and gains utility equivalent to $1,000,000 if she doesn’t die of cancer. Should she smoke, or refrain?
There are 8 possible worlds here, with different utilities and probabilities:
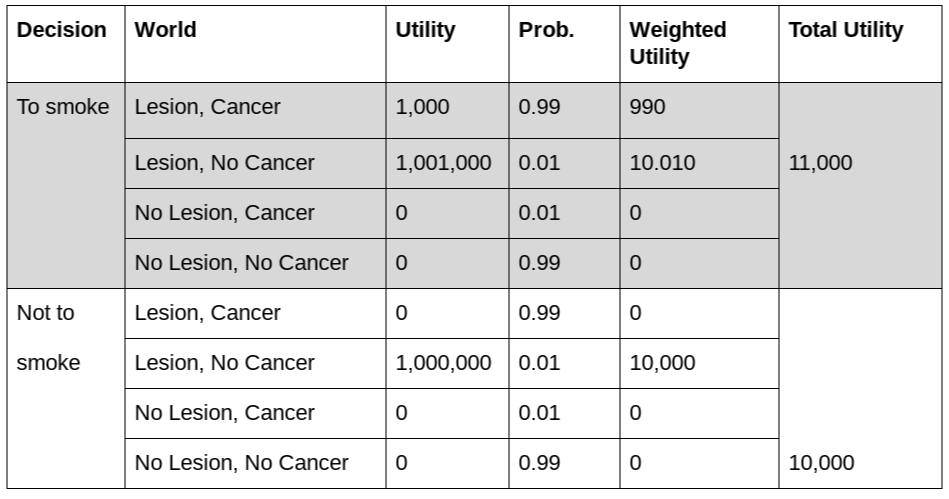
An agent who "decides" to smoke has higher expected utility than the one who decides not to, and this "decision" lets us learn which of the 4 possible worlds could be actual, and eventually when she gets the test results we learn which one is the actual world.
Note that the analysis would be exactly the same if there was a “direct causal link between desire for smoking and lung cancer”, without any “arterial lesion”. In the problem as stated there is no way to distinguish between the two, since there are no other observable consequences of the lesion. There is 99% correlation between the desire to smoke and and cancer, and that’s the only thing that matters. Whether there is a “common cause” or cancer causes the desire to smoke, or desire to smoke causes cancer is irrelevant in this setup. It may become relevant if there were a way to affect this correlation, say, by curing the lesion, but it is not in the problem as stated.
Because the problem states that only those afflicted with the lesion would gain utility from smoking:
an arterial lesion that causes those afflicted with it to love smoking
Anyway, the interesting worlds are those where smoking adds utility, since there is no reason for the agent to consider smoking in the worlds where she has no lesion.
That's not how the problem is usually interpreted. But you're also giving everyone without the lesion 0 utility for not having cancer? Why are you doing this and why include these cells if you are going to zero them out??? (And your criticism is that I am making things overly hard to follow!!!)
I agree that some of the rows are there just for completeness (they are possible worlds after all), not because they are interesting in the problem setup. How is the problem normally interpreted? The description in your link is underspecified.
But you're also giving everyone without the lesion 0 utility for not having cancer?
Good point. Should have put the missing million there. Wouldn't have made a difference in this setup, since the agent would not consider taking up smoking if they have no lesion, but in a different setup, where smoking brings pleasure to those without the lesion, and the probability of the lesion is specified, the probabilities and utilities for each possible world are to be evaluated accordingly.
The problem is usually set up so that they gain utility from smoking, but choose not to smoke.
In any case, you seem to have ignored the part of the problem where smoking increases chance of the lesion and hence cancer. So there seems to be some implicit normalisation? What's your exact process there?
The problem is usually set up so that they gain utility from smoking, but choose not to smoke.
Well, I went by the setup presented in the FDT paper (which is terrifyingly vague in most of the examples while purporting to be mathematically precise), and it clearly says that only those with the lesion love smoking. Again, if the setup is different, the numbers would be different.
In any case, you seem to have ignored the part of the problem where smoking increases chance of the lesion and hence cancer. So there seems to be some implicit normalisation? What's your exact process there?
Smoking does not increase the chances of the lesion in this setup! From the FDT paper:
an arterial lesion that causes those afflicted with it to love smoking and also (99% of the time) causes them to develop lung cancer. There is no direct causal link between smoking and lung cancer.
Admittedly they could have been clearer, but I still think you're misinterpreting the FDT paper. Sorry, what I meant was that smoking was correlated with an increased chance of cancer. Not that there was any causal link.
Right, sorry, I let my frustration get the best of me. I possibly am misinterpreting the FDT paper, though I am not sure where and how.
To answer your question, yes, obviously desire to smoke is correlated with the increased chance of cancer, through the common cause. If those without the lesion got utility from smoking (contrary to what the FDT paper stipulates), then the columns 3,4 and 7,8 would become relevant, definitely. We can then assign the probabilities and utilities as appropriate. What is the formulation of the problem that you have in mind?
Smoking lesion is an interesting problem in that it's really not that well defined. If an FDT agent is making the decision, then its reference class should be other FDT agents, so all agents in the same class make the same decision, contrary to the lesion which should affect the probability. The approach that both of us take is to break the causal link from the lesion to your decision. I really didn't express my criticism well above, because what I said also kind of applies to my post. However, the difference is that you are engaging in world counting and in world counting you should see the linkage, while my approach involves explicitly reinterpreting the problem to break the linkage. So my issue is that there seems to be some preprocessing happening before world counting and this means that your approach isn't just a matter of world counting as you claim. In other words, it doesn't match the label on the tin.
Smoking lesion is an interesting problem in that it's really not that well defined. If an FDT agent is making the decision, then its reference class should be other FDT agents, so all agents in the same class make the same decision, contrary to the lesion.
Wha...? Isn't like saying that Newcomb's is not well defined? In the smoking lesion problem there is only one decision that gives you highest expected utility, no?
Also, why are you ignoring the $1000 checkup cost in the cosmic ray problem? That's the correct way to reason, but you haven't provided a justification for it.
I tried to operationalize what
do the opposite of what she would have done otherwise
might mean, and came up with
Deciding and attempting to do X, but ending up doing the opposite of X and realizing it after the fact.
which does not depend on which decision is made, and so the checkup cost has no bearing on the decision. Again, if you want to specify the problem differently but still precisely (as in, where it is possible to write an algorithm that would unambiguously calculate expected utilities given the inputs), by all means, do, we can apply the same approach to your favorite setup.
My issue is that you are doing implicit pre-processing on some of these problems and sweeping it under the rug. Do you actually have any kind of generalised scheme, including all pre-processing steps?
I... do not follow. Unlike the FDT paper, I try to write out every assumption. I certainly may have missed something, but it is not clear to me what. Can you point out something specific? I have explained the missing $1000 checkup cost: it has no bearing on decision making because the cosmic ray strike making one somehow do the opposite of what they intended and hence go and get examined can happen with equal (if small) probability whether they take $1 or $100. If the cosmic ray strikes only those who take $100, or if those who take $100 while intending to take $1 do not bother with the checkup, this can certainly be included in the calculations.
I know that you removed the $1000 in that case. But what is the general algorithm or rule that causes you to remove the $1000? What if the hospital cost $999 if you chose $1 or $1000 otherwise.
I guess it seems to me that once you've removed the $1000 you've removed the challenging element of the problem, so solving it doesn't count for very much.
Let's try to back up a bit. What, in your mind, does the sentence
With vanishingly small probability, a cosmic ray will cause her to do the opposite of what she would have done otherwise.
mean observationally? What does the agent intend to do and what does actually happen?
We will consider a special version of the Smoking Lesion where there is 100% correlation between smoking and cancer - ie. if you have the lesion, then you smoke and have cancer, if you don't have the lesion, then you don't smoke and don't have cancer. We'll also assume the predictor is perfect in the version of Newcomb's we are considering. Further, we'll assume that the Lesion is outside of the "core" part of your brain, which we'll just refer to as the brain and assume that it affects this by sending hormones to it.
Causality
Notice how similar the problems are. Getting the $1000 or to smoke a cigarette is a Small Gain. Getting cancer or missing out on the $1 million is a Big Loss. Anyone who Smokes or Two-Boxes gets a Small Gain and a Big Loss. Anyone who Doesn't Smoke or One-boxes gets neither.
So while from one perspective these problems might seem the same, they seem different when we try to think about it casually.
For Newcomb's:
For Smoking Lesion:
Or at least these are the standard interpretations of these problems. The key question two ask here is why does it seem reasonable to imagine the predictor changing its prediction if you counterfactually Two-Box, but the lesion remaining the same if you counterfactually smoke?
Linkages
The mystery deepens when we realise that in Smoking Lesion, the Lesion is taken to cause both Smoking and Cancer, while in Newcomb's, your Brain causes both your Decision and the Prediction. For some reason, we seem more inclined to cut the link between Smoking and the Lesion than between your Decision and your Brain.
How do we explain this? One possibility is that for there Lesion there is simply more indirection - the link is Lesion -> Brain -> Decision - and that this pushes us to see it as easier to cut. However, I think it's worthwhile paying attention to the specific links. The link between your Brain and your Decision is a very tightly coupled link. It's hard to imagine a mismatch here without the situation becoming inconsistent. We could imagine a situation where the output of your brain goes to a chip which makes the final decision, but then we've added an entirely new element into the problem and so we hardly seem to be talking about the same problem.
On the other hand, this is much easier to do with the link between the Lesion and Brain - you just imagine the hormones never arriving. That would contradict the problem statement, but it isn't inconsistent physically. But why do we accept this as the same problem?
Some objects in problems "have a purpose" in that if they don't perform a particular function, we'll feel like the problem "doesn't match the description". For example, the "purpose" of your brain is to make decisions and the "purpose" of a predictor is to predict your decisions. If we intervene to break either the Brain-Decision linkage or the Brain-Predictor linkage, then it'll feel like we've "broken the problem".
In contrast, the Lesion has two purposes - to affect your behaviour and whether you have cancer. If we strip it of one, then it still has the other, so the problem doesn't feel broken. In other words, in order to justify breaking a linkage, it's not enough that it just be a past linkage, but we also have to be able to justify that we're still considering the same problem.
Reflections
It's interesting to compare my analysis of Smoking Lesion to CDT. In this particular instance, we intervene at a point in time and only casually flow the effects forward in the same way that CDT has. However, we haven't completely ignored the inconsistency issue since we can imagine whatever hormones the lesion releases not actually reaching the brain. This involves ignoring one aspect of the problem, but prevents the physical inconsistency. And the reason why we can do this for the Smoking Lesion, but not Newcomb's Problem is that the coupling from Brain to Lesion is not as tight as that from Decision to Brain.
The counterfactuals ended up depending on both the physical situation and the socio-linguistic conventions. How tightly various aspects of the situation were bound determined the amount of intervention that would be required to break the linkage without introducing an inconsistency, while the socio-linguistic conventions determined whether the counterfactual was accepted as still being the same problem.
Related: