Decomposition of attention patterns:

LayerNorm is a problem for understanding models, because it makes it hard to analyze content and position separately. Thankfully, the model wants to separate content and position, and so it mostly learns to mitigate this effect.

To handle LayerNorm, approximate the keys of the input at position $i$ for head $h$ on input $x$ as: 

$\frac{\text{key}\left[i\right]\left(x\right)}{\sqrt{d_{\text{model}}}}=\frac{W_{\text{E}}\left[x_i\right]W_K+W_{\text{pos}}\left[i\right]W_K}{|W_{\text{E}}\left[x_i\right]+W_{\text{pos}}\left[i\right]|}\approx \left(\frac{W_{\text{E}}\left[x_i\right]W_K+W_{\text{pos}}\left[n\right]W_K}{|W_{\text{E}}\left[x_i\right]+W_{\text{pos}}\left[n\right]|}\right)+\left(\frac{W_{\text{pos}}\left[i\right]W_K-W_{\text{pos}}\left[n\right]W_K}{\sqrt{|W_{\text{pos}}\left[i\right]{|}^2+{3.5}^2}}\right)=\frac{E[n,x_i]+P[n,i]}{\sqrt{d_{\text{model}}}}$

When these approximate keys are substituted in, the resulting approximate attention pattern is close to the true attention pattern, with a low total variation distance of about $0.05$ typically. This means that typically the true attention pattern, and the attention pattern obtained when using our modified keys, differ by a shift of 5% in attention mass.

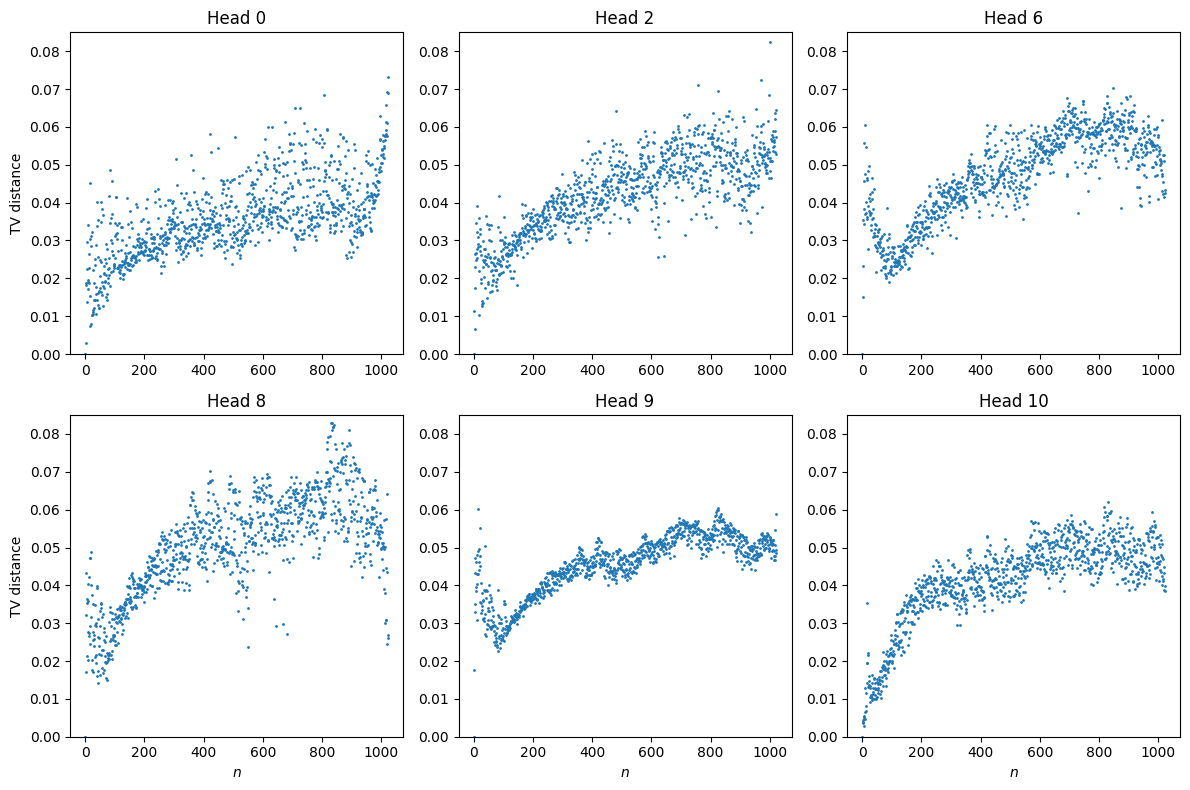
In practice, the approximate and true attention patterns end up being visually indistinguishable.

Positional kernels:

Define the positional kernel at position $n$ as:
$\begin{array}{cc}{\text{pos}}_{n,i,\text{query}\left[n\right]\left(x\right)}& =\text{Softmax}{\left(\frac{\text{query}\left[n\right]\left(x{)}^T\text{P}\right[1:n+1]}{\sqrt{d_{\text{value}}}}\right)}_i\end{array}$
 

And define:

${\text{content}}_{\text{E}\left[i\right]\left(x\right),\text{query}\left[n\right]\left(x\right)}=e^{\frac{\text{query}\left[n\right]\left(x{)}^{T}E\right[i\left]\right(x)}{\sqrt{d_{\text{value}}}}}$

The attention pattern attending from position n when using the approximate keys is given by:
$\begin{array}{cc}\text{attn\_approx}[n,i]\left(x\right)& =\frac{e^{{\text{attn\_approx}}_{\text{score}}[n,i]\left(x\right)}}{{\sum }_{j=1}^n{e}^{{\text{attn\_approx}}_{\text{score}}[n,j]\left(x\right)}}\\ & =\frac{{\text{pos}}_{n,i,\text{query}\left[n\right]\left(x\right)}\cdot {\text{content}}_{\text{E}\left[i\right]\left(x\right),\text{query}\left[n\right]\left(x\right)}}{{\sum }_{j=1}^n{\text{pos}}_{n,j,\text{query}\left[n\right]\left(x\right)}\cdot {\text{content}}_{\text{E}\left[j\right]\left(x\right),\text{query}\left[n\right]\left(x\right)}}\end{array}$

There are three categories of positional kernels in the first layer of GPT2-Small, shown below. These kernels are often translation equivariant, and they depend weakly on the particular query token.

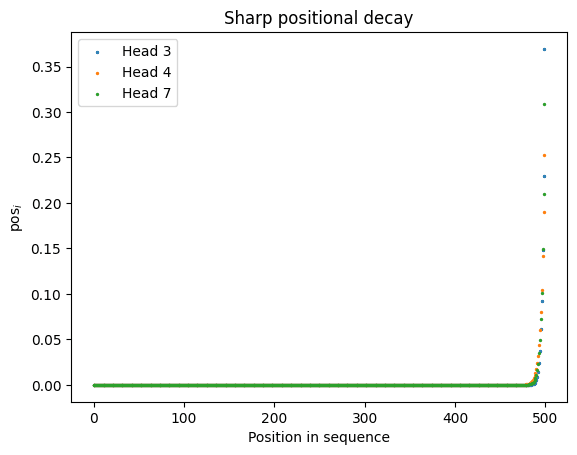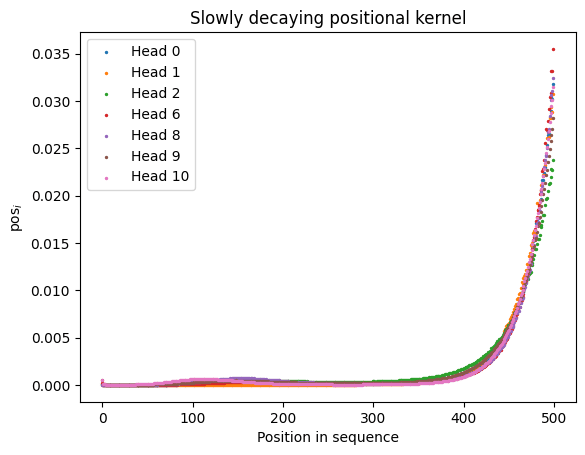
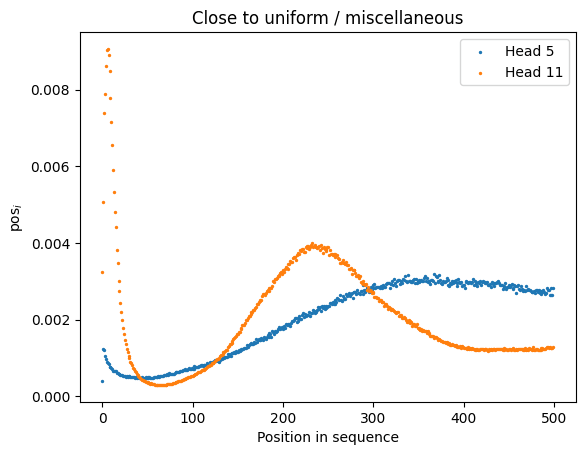Contextual circuit:

Stability of softmax denominators:

We have the softmax probability formula:

$\text{attn\_approx}[n,i]\left(x\right)=\frac{{\text{pos}}_{n,i,\text{query}\left[n\right]\left(x\right)}\cdot {\text{content}}_{\text{E}\left[i\right]\left(x\right),\text{query}\left[n\right]\left(x\right)}}{{\sum }_{j=1}^n{\text{pos}}_{n,j,\text{query}\left[n\right]\left(x\right)}\cdot {\text{content}}_{\text{E}\left[j\right]\left(x\right),\text{query}\left[n\right]\left(x\right)}}$

If we model the tokens in the sequence as drawn i.i.d according to some underlying distribution, we can apply concentration inequalities such as Hoeffding/Chebyshev to bound the probability that the softmax denominator deviates too far from its mean. In both cases, concentration is governed by ${\sum }_{i=1}^n{\text{pos}}_i^2$ together with a term measuring the content dependence of the attention scores.

${\sum }_{i=1}^n{\text{pos}}_i^2$ will be small when the positional kernel is spread out. So heads with wide positional kernels and attention scores depending weakly on content should have stable softmax denominators.

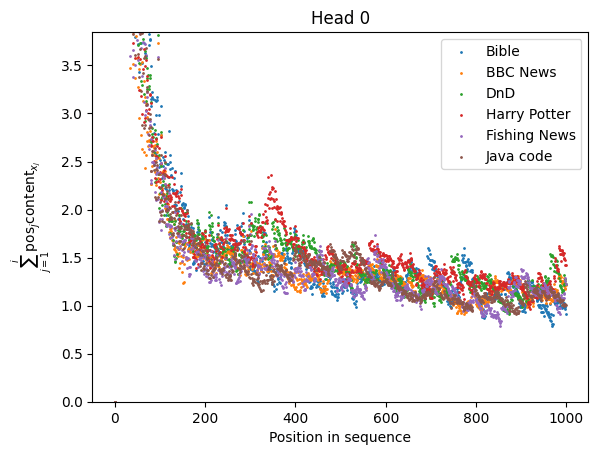
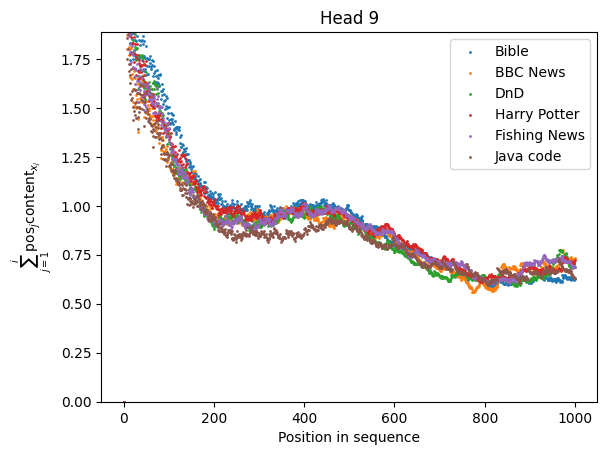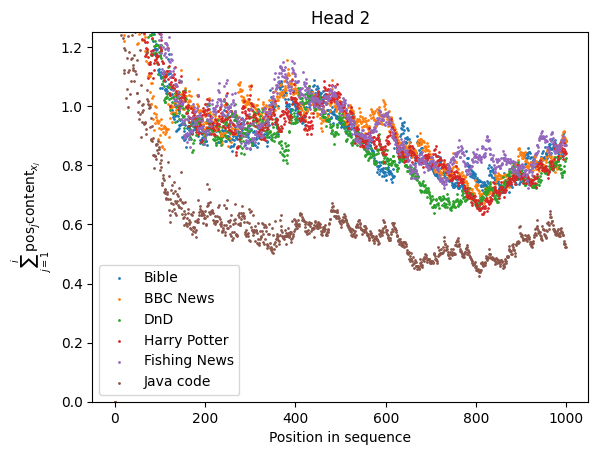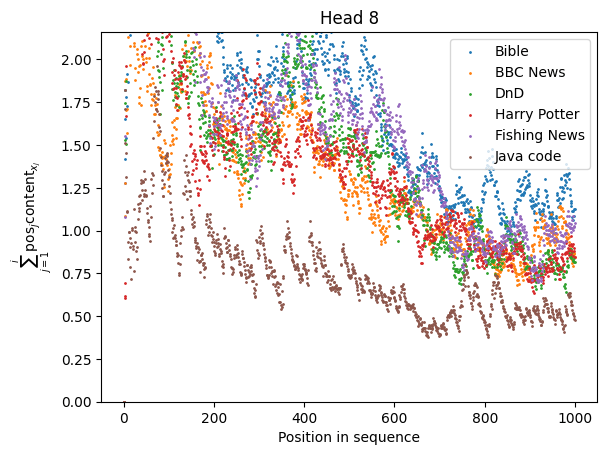
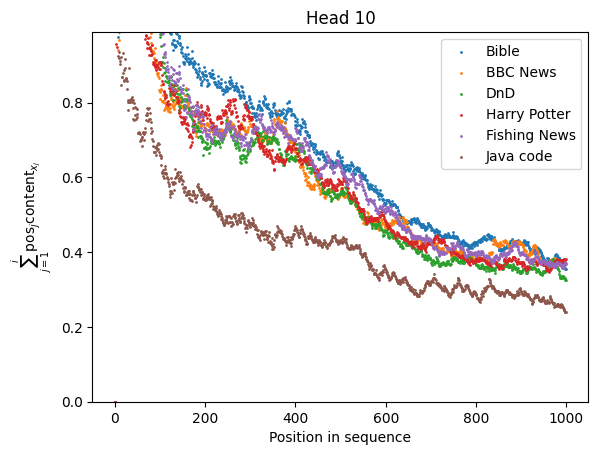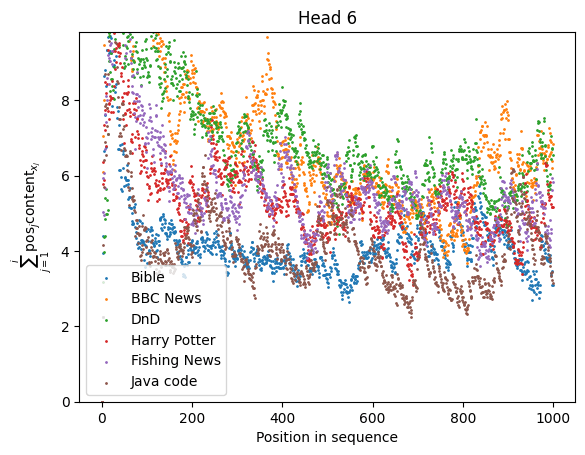The sequences used are drawn either from OpenWebText or from well-known books. There is an overall input-independent decay in the denominator for many of the heads, but the stability can be seen nonetheless. The worst behaved heads are Head $6$ and Head $8$, which depend on local keyword density, which fluctuates, but these heads are still significantly better behaved than heads with local positional kernels.

The relative stability of the softmax denominators for each of these heads tells us that their denominators are macroscopic properties of the surrounding text. Thus, we need to inject some information about the input distribution if we want to find the "effective circuit" which the model uses with high probability. We can't work in a fully weights-based manner, in other words.

We can inject this information by picking a representative calibration text for the distribution we are interested in, and sampling softmax denominators from this text. Once these softmax denominators have been chosen, because the heads (0, 2, 6, 8, 9, 10) have very similar positional kernels, we will be able to approximate their combined output by a positionally weighted summary ${\sum }_{i=1}^n{\text{pos}}_{n,i,\text{query}\left[n\right]\left(x\right)}\text{contribution}[n,\text{query}[n\left]\right(x),x_i]$. This summary will be a function of our calibrated softmax denominators, and I call this approximation the  "contextual circuit".

Contextual neurons:

Using the contextual circuit, we can efficiently identify neurons that respond to high-level contextual properties.

First, calibrate our circuit using a text with average keyword density and fix the query token to ' the' (which appears in many contexts). This one-time calibration gives us the softmax denominators we need.

Once calibrated, we can work entirely with the model weights - no more forward passes needed. Our frozen contextual circuit becomes a purely mathematical function that we can evaluate for any token.

For each of the 3072 first-layer MLP neurons, compute the "maximum token contribution" - $\text{max}\left[j\right]={sup}_{t\in [0,d_{\text{voc}}]}\text{contribution}[n,\text{query}[n\left]\right(x),t]\text{mlp}[:,j]$, for the $j$th neuron. Neurons with high maximum token contributions (I use threshold 5.0, leaving about 100 neurons) are sensitive to broad contextual patterns rather than just immediate neighboring tokens.

To understand what each contextual neuron detects, we can examine which tokens contribute most and least to it through our circuit. The vast majority correspond to interpretable patterns like particular topics, languages, or sentiment, from the training set.

So, after calibrating on one text, we can discover hundreds of contextual neurons using only weight-based analysis. The neurons found fire on contexts completely unrelated to the calibration text.

Commonwealth vs American English (Neuron 704):

Top 50 token contributions:  
[' pract', ' foc', ' recogn', ' UK', ' British', ' London', ' £', ' Australia', ' Britain', 'isation', ' Australian', ' emphas', ' favour', ' Labour', ' centre', ' util', ' BBC', ' Scotland', ' behaviour', ' defence', ' Manchester', ' colour', ' €', ' labour', ' analys', ' programme', ' Liverpool', ' Wales', ' Sydney', ' Scottish', ' neighbour', ' favourite', ' organisation', ' keen', ' organis', ' offence', ' whilst', ' Melbourne', ' MPs', '£', ' honour', ' summar', ' organisations', ' Isis', ' travelling', ' Defence', ' licence', ' NHS', ' Dublin', ' armour']

Bottom 50 token contributions: 
[' program', ' mom', ' favor', ' color', ' Center', ' center', ' defense', ' toward', ' Texas', ' favorite', ' organization', ' programs', ' behavior', ' analy', 'izes', 'izations', ' neighbor', ' labor', ' Color', 'avor', ' marijuana', ' organizations', ' Defense', ' license', ' attorney', ' neighborhood', ' realize', ' GOP', ' offense', ' realized', ' Seattle', ' honor', ' recognize', ' colors', ' gotten', ' folks', ' recognized', 'color', ' armor', ' organized', ' §', ' Oregon', 'sylvania', ' baseball', ' transportation', ' Iowa', ' downtown', ' flavor', '.--', ' accomplish']

This neuron classifies text as using Commonwealth English or American English, activating on Commonwealth English. It is an example where the bottom token contributions are as important to the function of the neuron as the top token contributions. Together, these token contributions allow the model to perform a kind of Naive Bayes classification of the text.