(Written with Matthew Mandelkern.)

TLDR: When asked to make interval estimates, people appear radically overconfident—far more so than when their estimates are elicited in other ways. But an accuracy-informativity tradeoff can explain this: asking for intervals incentivizes precision in a way that the other methods don’t. 

Pencils ready!  For each of the following quantities, name the narrowest interval that you’re 90%-confident contains the true value:

The population of the United Kingdom in 2020.

The distance from San Francisco to Boston.

The proportion of Americans who believe in God.

The height of an aircraft carrier.

Your 90%-confidence intervals are calibrated if 90% of them contain the true value. They are overprecise if less than 90% contain it (they are too narrow), and underprecise if more than 90% do.

We bet that at least one of your intervals failed to contain the true value.^[1] If so, then at most 75% of your intervals contained the correct answer, making you overprecise on this test.

You’re in good company. Overprecision is one of the most robust findings in judgment and decision-making: asked to give confidence intervals for unknown quantities, people are almost always overprecise. 

The standard interpretation? People are systematically overconfident: more confident than they rationally should be. Overconfidence is blamed for many societal ills—from market failures to polarization to wars.  Daniel Kahneman summed it up bluntly: “What would I eliminate if I had a magic wand? Overconfidence.”

But this is too quick. There are good reasons to think that when people answer questions under uncertainty, they form guesses that are sensitive to an accuracy-informativity tradeoff: they want their guess to be broad enough to be accurate, but narrow enough to be informative.  

When asked who’s going to win the Republican nomination, “Trump” is quite informative, but “Trump or DeSantis” is more likely to be accurate.  Which you guess depends on how you trade off accuracy and informativity: if you just want to say something true, you’ll guess “Trump or Desantis”, while if you want to say some thing informative, you’ll guess “Trump”.

So accuracy and informativity compete. This competition is especially stark if you’re giving an interval estimate. A wide interval (“the population of the UK is between 1 million and 1 billion”) is certain to contain the correct answer, but isn’t very informative. A narrow interval (“between 60 and 80 million”) is much more informative, but much less likely to contain the correct answer.

We think this simple observation explains many of the puzzling empirical findings on overprecision.^[2]

The Empirical Puzzle

The basic empirical finding is that people are overprecise, usually to a stark degree. Standardly, their 90%-confidence intervals contain the true value only 40–60% of the time.  They are also almost never under-precise. 

In itself, that might simply signal irrationality or overconfidence. But digging into the details, the findings get much more puzzling:

1) Intervals are insensitive to confidence level

You can ask for  intervals at various levels of confidence. A 90%-confidence interval is the narrowest interval that you’re 90%-confident contains the true value; a 50%-confidence interval is the narrowest band that you’re 50%-confident contains it, etc.

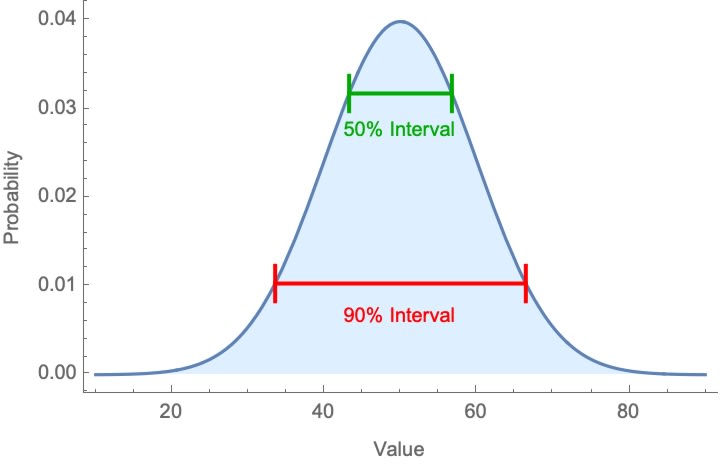
A standard finding is that people give intervals of very similar width regardless of whether they’re asked for 50%-, 90%-, or even 99%-confidence intervals.  For example, this study found that the widths of 99%-confidence intervals were statistically indistinguishable from those of 75%-confidence intervals.

This is puzzling. If people are giving genuine confidence intervals, this implies an extremely implausible shape to their probability distributions—for instance, like so:

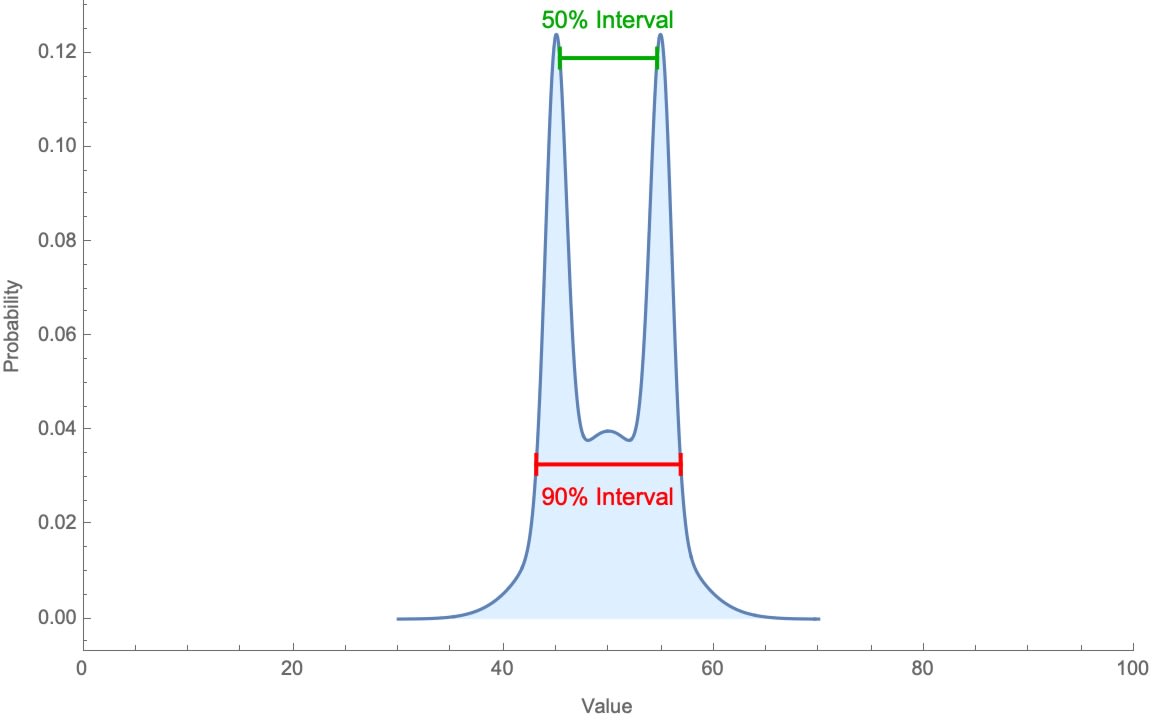
2) People are less than 90%-confident in their own 90%-confidence intervals

In a clever design, this study asked people for ten different 90%-confidence intervals, and then asked them to estimate the proportion of their own 90%-confidence intervals that were correct.  If they were giving genuine confidence-intervals, they should’ve answered “9 of 10”. 

Instead, the average answer was 6 of 10.  That indicates that people don’t understand the question (“What’s your 90%-confidence interval?”), and in fact are closer to 60% confident in the intervals that they give in response to it.

3) People are more overprecise when they give intervals than estimates

The elicitation method we’ve used so far is the interval method: asking people to name the interval they’re (say) 90%-confident contains the true value.  

But another way to elicit a confidence interval is the two-point method: first ask people for the number B that they’re exactly 95%-confident is below the true value, and then for the number A that they’re exactly 95%-confident is above the true value.  The interval [B,A] is then their 90%-confidence interval.

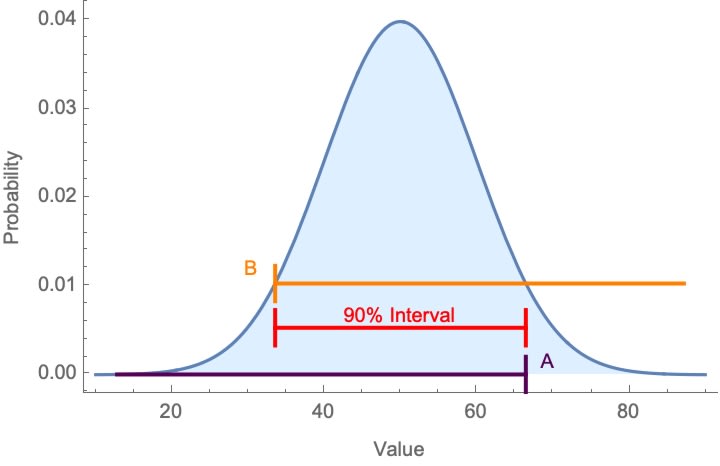
These two methods should come to the same thing.^[3]

But they don’t. For example, this study elicited 80%-confidence intervals using both methods. Intervals for the interval method contained the true value 39% of the time, while those for the two-point method contained it 57% of the time.

This finding generalizes. A different way to test for overconfidence (generalizing the two-point method) is the estimation method: have people answer a bunch of questions and rate their confidence in their answers; then check what proportion were correct of the answers that they were 90%-confident in.  If they were calibrated, this ”hit rate” should be 90%.

The main finding of the estimation method is the hard-easy effect. For (hard) tests with low overall hit rates, people over-estimate their accuracy—less than 90% of their 90%-confident answers are correct. But for (easy) tests with high overall hit rates, people under-estimate their accuracy (more than 90% are correct).   This contrasts sharply with the interval method, which virtually never finds underprecision.

Notice: these empirical findings are puzzling even if you think people are irrational.  After all, if people are simply overconfident, then these different ways of eliciting their confidence should lead to similar results. Why don’t they?

The Accuracy-Informativity Tradeoff

Our proposal: the interval method has a unique question-structure that incentivizes informative answers. Given the accuracy-informativity tradeoff in guessing, this makes people especially prone to sacrifice accuracy (hit rates) when giving intervals. 

To see how this works, we need a theory of guessing on the table. 

Consider this simple scenario: Three candidates are running for mayor: Joe, Don, and Ron.  Current predictions (which you trust) give Joe a 45% chance of winning, Don a 35% chance, and Ron a 20% chance.

A friend asks you: “What do you think will happen in the election?” 

There are a whole lot of interesting patterns in what guesses are natural-vs.-weird in such contexts—see this post, this paper by Ben Holguín, and this follow-up for more details. Here we’ll get by with a couple observations.

Guesses take place in response to a question.  The complete answers to the question are maximally specific ways it could be resolved—in our case, “Joe will win”, “Don will win”, and “Ron will win”.  Partial answers are combinations of complete answers, e.g. “Either Joe or Don will win”:

Guesses are accurate if they’re true.  They’re informative to the extent that they rule our alternative answers to the question: “Joe will in” is more informative than “Joe or Don will win”, since the former rules out two alternative (Don, Ron) and the latter rules out only one (Ron).

Crucially, informativity is question-sensitive.  Although “Joe will win, and he’s bald” is more specific than “Joe will win”, it’s not more informative as an answer to the question under discussion.  In fact, the extra specificity is odd precisely because it adds detail without ruling out any alternative answers.

On this picture of guessing, people form guesses by (implicitly) maximizing expected answer value, trading off the value of being accurate with the value of being informative. 

“Joe will win” maximizes this tradeoff when you care enough about informativity, for this drives you to give a specific answer. In contrast, “Don will win” is an odd guess because it can’t maximize this tradeoff given your beliefs: it’s no more informative than “Joe will win” (it rules out the same number of alternatives) and is strictly less likely to be accurate (35% vs. 45%).

Meanwhile, “Joe or Don will win” or “I don’t know—one of those three” can each maximize this tradeoff when you care less about informativity and more about accuracy.

Notice that question-sensitivity implies that what guesses are sensible depends on what the question is.  Although “Joe will win” is a perfectly fine answer to “Who do you think will win the election?”, it’s a weird answer to the question, “Will Joe win or lose the election?”. After all, that question has only two possible answers (“Joe will win” and “Joe will lose”), both are equally informative, but “Joe will lose” is more (55%) likely to be accurate than “Joe will win (45%).

On this picture of guessing, part of getting by in an intractably uncertain world is becoming very good at making the tradeoff between accuracy and informativity.  We’ve argued elsewhere that this helps explain the conjunction fallacy.

It also helps resolve the puzzle of overprecision.

Resolving the Puzzle

Key fact: Different ways of eliciting confidence intervals generate different questions, and so lead to different ways of evaluating the informativity of an answer.

If we ask “What interval does the population of the UK fall within?”, then the possible complete answers to the question are roughly:^[4]

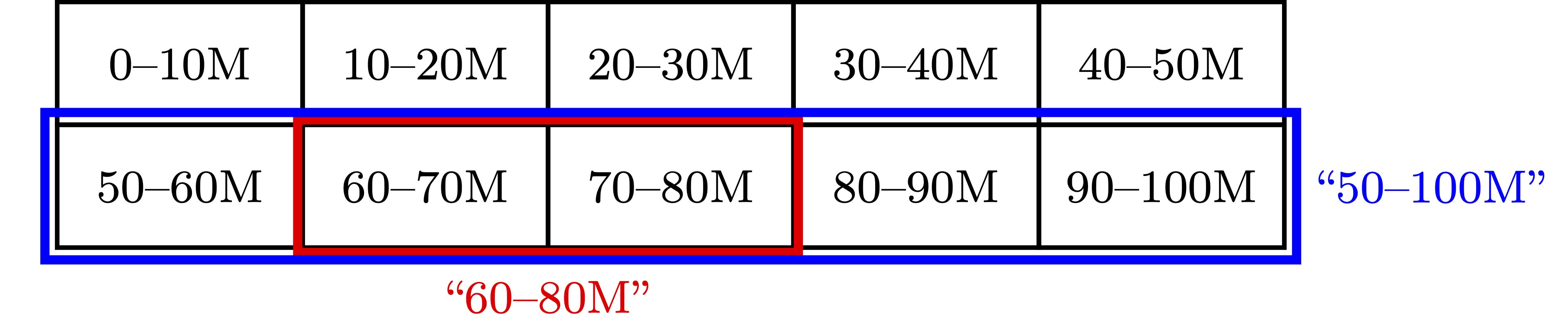
Possible answers are then combinations of these complete answers. Narrow guesses are more informative: “60–80 million” rules out 8 of the 10 possible answers, while “50–100 million” rules out only 5 of them.  As a result, the pressure to be informative is pressure to narrow your interval.

In contrast, suppose we ask “How confident are you that the true population of the UK is at least 60 million?”, now the possible answers are:

Note: in response to this question, “95% confident” is no more informative than (eg) “50% confident”—both of them rule out 20 of the 21 possible answers.

This observation can explain our three puzzling findings:

1) Intervals are insensitive to confidence level

Recall that people give extremely similar width to their intervals regardless of what level of confidence is asked for.  We should expect this.

The basic idea of the guessing picture is that our practice of eliciting guesses uses a wide range of vocabulary.  In our above election example, the following are all natural ways of eliciting a guess:

“What do you think will happen?”

“Who’s likely to win?”

“What should we expect?”

“Who’s your money on?”

“How’s this going to play out?”

And so on.

On this picture, when we ask questions under uncertainty in everyday thought and talk, we’re almost always asking for guesses—asking for people to balance accuracy and informativity.  Thus it’d be unsurprising if people focus on the structure of the question (whether it’s more informative to give a narrower interval), and largely ignore the unfamiliar wording (“90%-confidence interval” vs. “80%-confidence interval”) used to elicit it.

2) People are less than 90%-confident in their own 90%-confidence intervals

Recall that when asked how many of their own 90%-confidence intervals were correct, people estimated that around 60% were.  We should expect this.

The responses they give to the interval-elicitation method aren’t their true confidence intervals—rather, they’re their guesses, which involve trading some confidence for the sake of informativity.

If we change the question to “How many of the intervals you gave do you think contain the true value?”, now the possible answers range from “0 out of 10” to “10 out of 10”. “9 of 10” is no longer more informative than “6 of 10”—both are complete answers. This removes the incentive to sacrifice accuracy for informativity.

3) People are more overprecise when they give intervals than estimates

Recall that the interval method elicits more overprecision than the two-point method.  We should expect this.

When asked what interval the population of the the UK falls within, “60–80 million” is more informative than “50–100 million”, since it rules out more possible answers. 

But when asked for the number B that you’re 95% confident is below the true value, “60 million” is no more informative than “50 million”—both are complete answers to that question.^[5] Similarly when asked for the number A that you’re 95%-confident is about the true value—“80 million” is no more informative than “100 million”.

Upshot: the drive for informativity pushes toward a narrower interval when eliciting intervals directly, but not when using the two-point method. That’s why the former leads to more overprecision.

We can simulate the results of agents who form intervals using our preferred way of modeling the accuracy-informativity tradeoff. We can use agents whose probabilities are well-calibrated—their genuine 90%-confidence intervals contain the true value 90% of the time—but who give guesses rather than confidence-intervals. 

Here’s how often their intervals contain the true value (“hit rate”) as we vary the value of informativity:

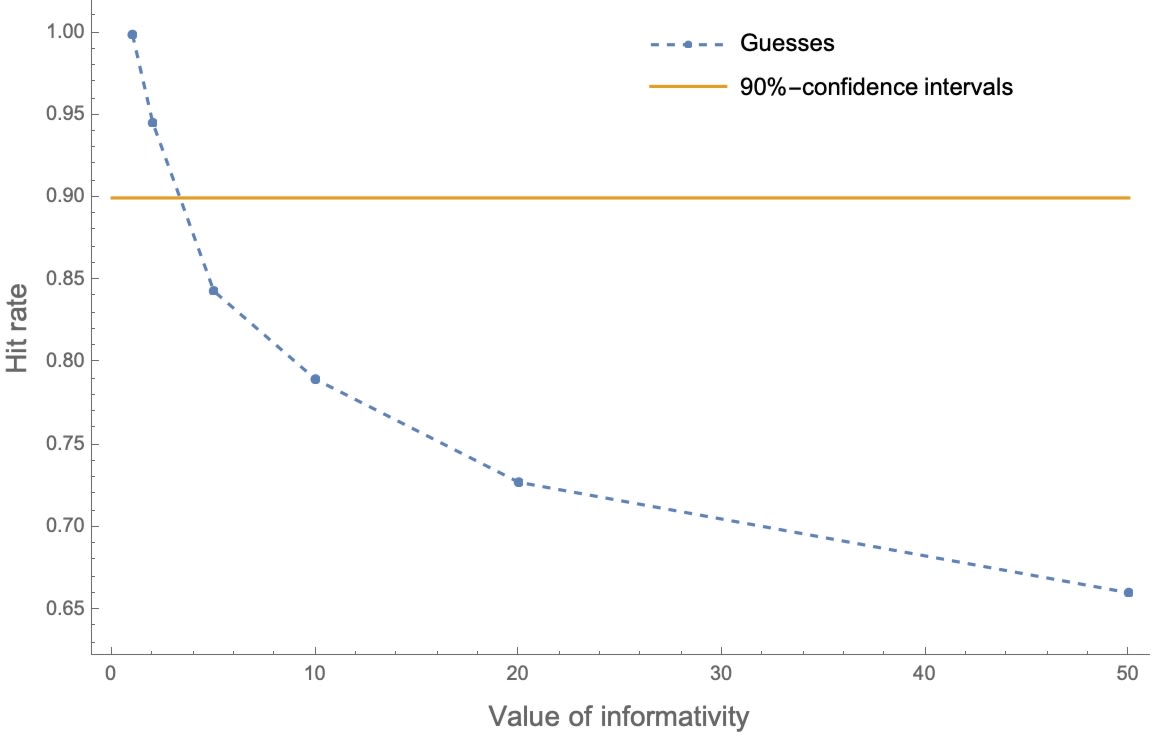
Stark degrees of overprecision are exactly what we should expect.^[6]

So is this rational?

Two points.

First, many researchers claim that the best evidence for overconfidence comes from the interval-estimation method, since other methods yield mixed results.  But since interval estimation is uniquely situated to reward informativity over accuracy, there’s reason for caution.  The empirical evidence for overconfidence is more complicated than you'd think.

Second, you might worry that the irrationality comes at an earlier step: why are people guessing rather than giving genuine confidence intervals? 

Granted, people are misunderstanding the question. But insisting that this is irrational underestimates how important informativity is to our everyday thought and talk. 

As other authors emphasize, in most contexts it makes sense to trade accuracy for informativity.  Consider the alternative: widening your intervals to obtain genuine 90% hit rates.  Empirical estimates suggest that to do so, you’ve had to widen your intuitive reactions by a factor of between 5 and 17 times.  

Suppose you did.  Asked when you’ll arrive for dinner, instead of “5:30ish” you say, “Between 5 and 8”.  Asked how many people will be at the party, instead of “around 10” you say, “Between 3 and 30”.  Asked when you’ll reply to my email, instead of “next week” you say, “Between 1 day and 3 months”.

These answers are useless.  They are in an important sense less rational than the informative-but-error-prone guesses we actually give in everyday thought and talk.

That, we think, is why people are overprecise. And why, on the whole, it makes sense to be so.

What next?

For a detailed discussion of just how subtle it is to move from observations of miscalibration to conclusions of irrationality, see this paper by Juslin et al.

For a great summary piece on overprecision, see this paper by Don Moore and colleagues.

For more on the accuracy-informativity tradeoff, see this blog post and this paper.

1. ^{^}

   Answers: 67.8 million; 2704 miles; 81%; and 252 feet.

2. ^{^}

   We’re taking inspiration from Yaniv and Foster 1995, though we implement the idea importantly differently. Two main points: our measure of informativity (1) allows for discrete (rather than interval-valued) questions, and (2) never incentivizes giving an interval that you know doesn’t contain the wrong answer (unlike their measure).

3. ^{^}

   Assuming the distribution is unimodal and peaked in the middle.

4. ^{^}

   Binning populations by 10-millions and upper-bounding it at 100M, for simplicity. We assume that when asked for an interval, the goals of the conversation pinpoint a maximal level of fineness of grain.

5. ^{^}

   Note: “40–60M“ is an answer to the lower-bound question, but experimenters usually force people to give a complete answer to what they’re lower bound is, rather than letting them choose an interval for the bound.

6. ^{^}

   The “Value of Informativity” is their “J-value” (see section 3 of this paper). Although this is a parameter we don’t expect people to have direct intuitions about, you need a J-value of about 6 for the optimal accuracy-informativity tradeoff in our election case to favor guessing “Joe will win” over “Joe or Don will win”. Thus a J-value of 3 or 4—the threshold at which people become overprecise—is quite modest.  Indeed, many sensible guesses require much higher J-values: if Joe had a 50% chance of winning, Don had a 10% chance of winning, and 40 other candidates had 1% each chance of winning, then the J-value required to guess “Joe will win” is over 2000.