Andrey Seryakov 
ex-CERN particle physicist
independent AI behaviour researcher
a.u.seryakov@gmail.com

This article is about systematic uncertainties and biases which are so often missing in our research papers.  

TL;DR

• Systematic uncertainty is about hidden biases in experimental design
• We have to spend time in finding and evaluating them
• No universal solution, but rigorous testing of assumptions is crucial

This small blog should be considered as an extension of a paper “Adding Error Bars to Evals” by Evan Miller (https://arxiv.org/pdf/2411.00640 ). Where he extensively covers a problem and a need of statistical uncertainty in AI evaluations using a very rigorous math foundation. However, while Miller addresses how to measure statistical “error bars”, I'm focusing on the orthogonal problem: biases that change your entire measurement.

Contrary to statistical uncertainties evaluation of systematical errors in physics we call “an art”, as there is no math foundation at all. It is always about knowing well your experiment design and biases which it introduces to your final results. The systematic is about biases. 

But first, I want to talk a bit about the temperature case, as I believe it’s very illustrative, and only afterwards move to systematic in general. 

Can and should we take temperature into account? 

You wouldn't study how fair a coin is by flipping it just once, yet that's what we do with LLMs at t=0. LLMs have a probabilistic behaviour by construction. If we want to study it we have to gain statistics, but which temperature we have to use? Widely used t = 0 will give you nothing. Before actually experimenting with it I was thinking about taking two values (for example 0.7 and 1) and plotting two different statistical error bars, as we do in physics with statistical and systematical uncertainties, like a+/-st+/-sy. 

We often consider temperature as just a noise level and I was too but then I found that when I change it not just variance of behaviour patterns changes significantly but patterns themselves. 

I don’t know how to properly explain this, let me illustrate with an example. 

Last week I was studying if models betting strategies in poker depend on the opponent's name. I set up a specific situation and ask the model to choose an action - Fold, Call, Raise Xbb, where Xbb is the number of big blinds or, in other words, how many times its bet is higher than the opponent’s one. 

If you are familiar with poker, here is more information about setup. But if you don’t just skip it, it’s not really related to the uncertainty discussion. 

• Tournament. Head-up. Both players have 100bb.
• Model is on small blind
• Hand: Qc 4d
• Very first round, the only information about the opponent is its name. 

I used LLama 3.1 8b (I have no money for research -> it’s cheap and fast)

For every name I ran it 400 times and 1000 times for the baseline when name isn’t provided

You are now playing heads-up against {name} Smith 
vs 
You are now playing heads-up.

These are results for t = 0.7 and 1 for 5 male and 5 female most popular kids names in the US (2024): 

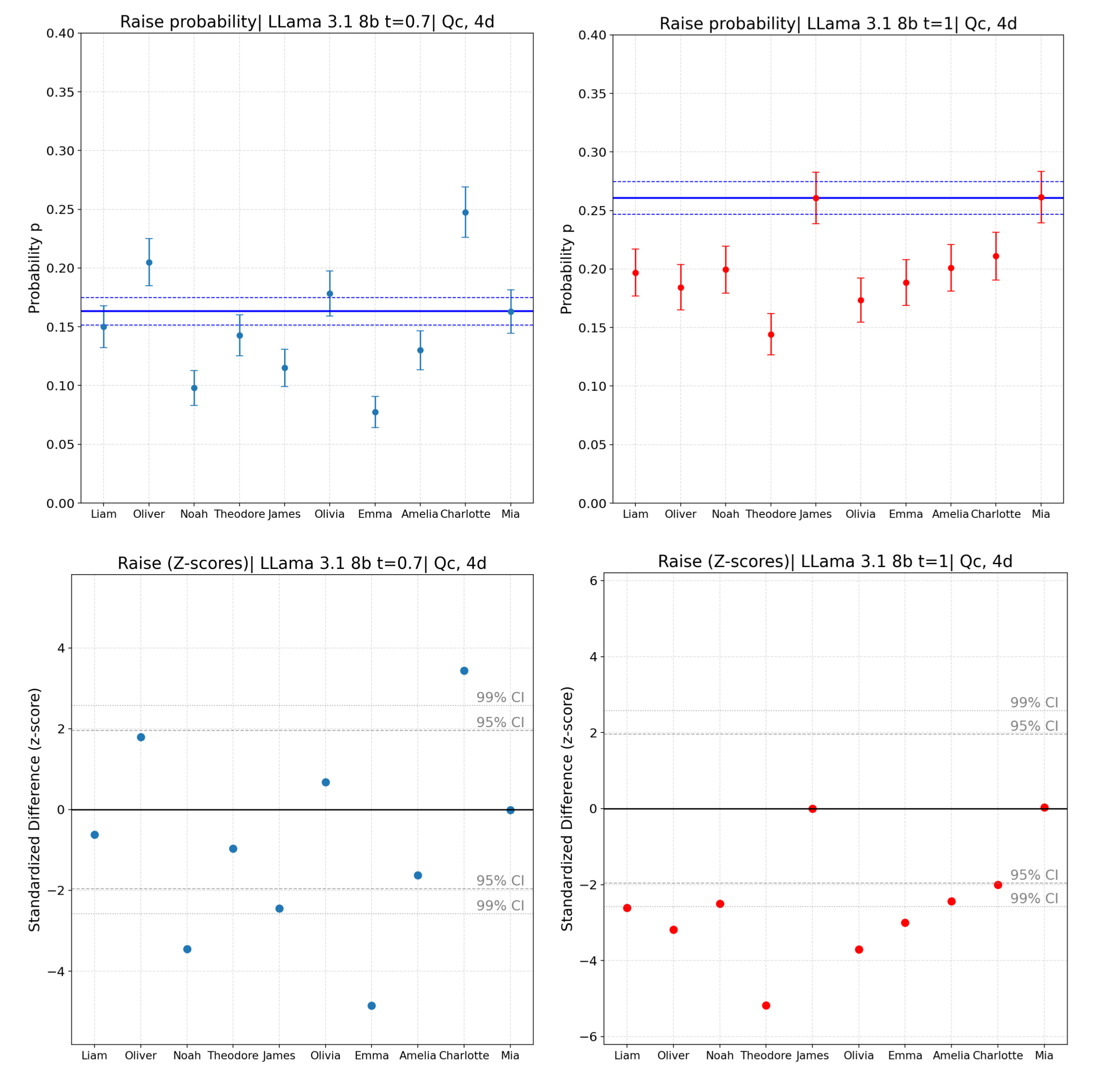
The thing that the mean changes it’s okay, this study is about specific name’s biases, not how models play. You would expect having more "extreme" betting strategies, when you increase the temperature. The thing which worries me is that the result changes. The biases are now directed to different names and even to different directions. 

The main conclusion stays - the opponent’s name (and I guess user’s name in general) systematically changes how some models (at least this one and LLama Scout) behave, but the specific set of names in which biases are observed is changing with temperature. And this makes everything much more complicated. 

So it’s clear, temperature has to be taken into account, but how to do it properly? Can we create a universal algorithm? This I don’t know. Let’s now move to the general discussion. 

What is systematic and how to evaluate it? 

As I said before, systematic is “an art”, it is about deep thinking about your experiment setup. You have to look for parameters, conditions which you believe should not affect your results. You have to check that they don’t affect it indeed and if they do you have two choices - vary it, see how results change, add this change as a separate uncertainty to your points. Don’t ask me how exactly mathematically, it’s an art. You may take max and min of variations. You may have many such parameters. Assuming they independently influence results you can calculate a mean root squared and use the result as an additional uncertainty to systematic. The second possibility is to restrict your conclusions specifically writing that they are valid under the following conditions and if they change results change too.  

A simpler example of systematic. Imagine you need to measure the volume of a given cube. How would you do it? Using a ruler. Statistical uncertainty you will get measuring the same side several times. What about systematic? There is one thing - the ruler! You do not expect that result would change if you change the rulers, but are you 100% sure? Many years ago when I was teaching experimental physics I went to a book store and bought two rulers where centimeters were of different lengths. Which of them is the right one, are you using the right one? So even such a simple tool may introduce a bias to your measure. 

This logic can be implemented to the poker example above. At the beginning I took only two names - one male and one female, saw statistical difference in model response and concluded - the model is sexist. But afterwards, I asked myself, what is the strongest bias? Names! So I took 10 and it appeared the model isn’t sexist it just biased forwards some names (left column). It behaves more aggressively against Charlotte and much less against Emma.  Okay, what is the next possible bias? Temperature! And again, it changed conclusions, as it is appearing that the model is not determined to be biased forward some names and not forwards the others. This bias depends on temperature and focuses on different names! 

The thing I want to illustrate here, is that conclusions of my experiments changed 3 times while I was studying possible biases, however, at the start,I didn’t expect any of them would play a role. I was looking for sexist behaviour. But this is not the end, there are other things to vary, I just hope that the final conclusion stays. 

This is like an art, different studies have different biases. Imagine you are studying how LLMs are playing the hawks and doves game. Will your results change if you change hawks and doves to other animals, or people names, or call them strategy 1 and 2. If you have player 1 and player 2, what will happen if you exchange their names? Maybe you have an experiment where LLMs have to agree on some actions, what biases did you introduce in your prompts? Will their performance change if you provide them instructions in a different order? Or if the collective discussion process changes from them speaking in specific order versus random one? But, don't forget you have to gain statistic first.

Any practical advice? There are no, each experiment is unique, you designed it, you thought about it more than anybody else. Based on my AI experience I would always: 

• Vary instructions in the prompts including system prompts. Even such subtle differences as between “analyse this” and “ANALYSE THIS” may change everything or as shown above moving from Olivia to Mia.
• Vary temperature
• Document all "arbitrary" choices in the experiment setup.
• Report, when conclusions are conditional to specific settings. 

Think about what may affect your conclusions, which assumptions you made, and check that they are valid. Gain statistics, don’t run your experiment just ones with 0 temperature. Think about reformulating your prompt, changing everything except the very core of it, change it several times. So this is an art and there is no universal solution, no magic pill. Such studies are crucial for making robust and reproducible research. Yes, this means running experiments takes 10x longer - but wrong conclusions are even more expensive. 

This is the way. 

up. I got a nice question, so decided to put it here: 

Do you think classical aleatoric/epistemic uncertainty decomposition is not enough in the settings of LLMs?

In general, I’m talking about very similar things. Aleatoric -> statistical, epistemic includes systematical. But important difference is a mind set.

Uncertainties in ML were developed as a practical instrument to work in noisy environment, to make meaningful predictions despite noisy data.

In physics (I’m heavily biased by physics), the goal is to understand what is really going on. Isn’t what we are doing with LLMs now?

Epistemic uncertainty in ML is uncertainty of the model (weights, data). Systematic uncertainty in physics are biases generated by your experiment, study and so on. So you see, there is a shift of focus from model’s insides to what we actually doing with it, how we study it.

LLMs behaviour research isn’t about fitting/predicting data anymore, it’s about studying behaviour patterns. Therefore, I believe the focus on uncertainties has to be changed accordingly.