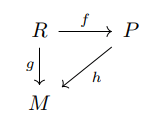Homomorphically encrypted consciousness and its implications
17J Bostock
2Steven Byrnes
1jessicata
1Ben Livengood
2jessicata
3Ben Livengood
2jessicata
3Ben Livengood
9Gunnar_Zarncke
4jessicata
2Gunnar_Zarncke
2jessicata
2Gunnar_Zarncke
4jessicata
2Gunnar_Zarncke
4jessicata
2Gunnar_Zarncke
4jessicata
9Tapatakt
2jessicata
2Gurkenglas
2jessicata
9plex
4jessicata
4plex
4plex
3RussellThor
4Adele Lopez
2jessicata
2Adele Lopez
2jessicata
4Adele Lopez
2jessicata
3Mitchell_Porter
2jessicata
3robo
3jessicata
3robo
2jessicata
3Joey KL
2jessicata
2Richard_Kennaway
1red75prime
2jessicata
1red75prime
1williyamyam
1robo
2jessicata
New Comment
I actually think that A is the most intuitive option. I don't see why it should be possible for something which knows the physical state of my brain to be able to efficiently compute the contents of it.
Then again, given functionalism, perhaps it's the case that extracting information about the contents of the brain from the encrypted computation is not as hard as one might think. The encryption is just a reversible map from one state space to another. If an omniscient observer can extract the contents of a brain by assembling a causal model of it in un-encrypted phase space, why would it struggle to build the same casual model in encrypted phase space? If some high-level abstractions of the computation are what matter, then the difficult part is mostly in finding the right abstractions.
I don't see why it should be possible for something which knows the physical state of my brain to be able to efficiently compute the contents of it.
I think you meant "philosophically necessary" where you wrote "possible"? If so, agreed, that's also my take.
If an omniscient observer can extract the contents of a brain by assembling a causal model of it in un-encrypted phase space, why would it struggle to build the same casual model in encrypted phase space?
I don’t understand this part. “Causal model” is easy—if the computer is a Turing machine, then you have a causal model in terms of the head and the tape etc. You want “understanding” not “causal model”, right?
If a superintelligence were to embark on the project of “understanding” a brain, it would be awfully helpful to see the stream of sensory inputs and the motor outputs. Without encryption, you can do that: the environment is observable. Under homomorphic encryption without the key, the environmental simulation, and the brain’s interactions with it, look like random bits just like everything else. Likewise, it would be awfully helpful to be able to notice that the brain is in a similar state at times t₁ versus t₂, and/or the ways that they’re different. But under homomorphic encryption without the key, you can’t do that, I think. See what I mean?
To be clear in path A I'm imagining that the omniscent observer knows not just physics, but all of reality. By step 10 we already have that physical omniscience + physical (BQP) computation isn't enough to derive mental states. (So it's a question of whether the mental states / abstractions are "real", encoded somewhere in reality even if not properly in physics)
I think the extra difficulty with encrypted phase space is the homomorphic encryption presumably makes it computationally intractable? If it really is intractable then "search over the right abstractions" is going to be computationally hard.
It's possible to alter a homomorphic computation in arbitrary ways without knowing the decryption key.
An omniscient observer can homomorphically encrypt a copy of themselves under the same key as the encrypted mind and run a computation of its own copy examining every aspect of the internal mental states of the subject, since they share the same key.
If there are N homomorphically encrypted minds in reality then the omniscient observer will have to create N layers of homomorphic computation in order for the innermost computation to yield the observation of all N minds' internal states, each passed in turn to a sub-computation, and relying on the premise that homomorphically encrypted minds are conscious for the inner observer to be conscious.
The question is whether encoding all of reality and homomorphically encrypting it necessarily causes a loss of fidelity. If yes, one of the trilemmas still holds. Otherwise there's no trilemma and the innermost omniscient observer sees all of reality and all internal mental states. I'd argue that for a meaningful omniscient observer to exist it is the case that encoding of reality (into the mind of the observer) must not result in a loss of fidelity. There could be some edge-cases where a polynomial amount of fidelity is lost due to the homomorphic encryption that wouldn't be lost to the "natural" omniscient observer's encoding of reality, but I think it stretches the practical definition of omniscience for an observer.
I think the argument extends to physics but the polynomial loss of fidelity is more likely to cause problems in a very homomorphically-encrypted-mind-populated universe.
Hmm... I'm not sure if I'm imagining what you are, but wouldn't the omniscient observer need to know the key already to encrypt themselves? (If reality somehow contains the key, then I suppose omniscience about reality is enough, but omniscience about physics isn't.)
It is true that being more encrypted is more compatible with being omnsiscent. It's strange because base physics is often thought of as the more omniscent layer. Like, I still think you get "mind exceeds physics" (hence the trilemma) since the omniscient observer you're positing isn't just working in base level physics, they have somehow encrypted themselves with the same key (which is not tractably available). But it seems if they knew the key they wouldn't even need to encrypt themselves to know anything additional.
To perform homomorphic operations you need the public key, and that also allows one to encrypt any new value and perform further hidden computations under that key. The private key allows decryption of the values.
I suppose you could argue that the homomorphically encrypted mind exists ala mathematical realism even if the public key is destroyed, but it would be something "outside reality" computing future states of the encrypted mind after the public key is no longer available.
Oh, maybe what you are imagining is that it is possible to perceive a homomorphic mind in progress, by encrypting yourself, and feeding intermediate states of that other mind to your own homomorphically encrypted mind. Interesting hypothetical.
I think with respect to "reality" I don't want to be making a dogmatic assumption "physics = reality" so I'm open to the possibility (C) that the computation occurs "in reality" even if not "in physics".
After doing some more research I am not sure that it's always possible to derive a public key knowing only the evaluation key; it seems to depend on the actual FHE scheme.
So the trilemma may be unaffected by this hypothetical. There's also the question of duplication vs. unification for an observer that has the option to stay at base level reality or enter a homomorphically encrypted computation and whether those should be considered equivalent (enough).
I think step 10 overstates what is shown. You write:
“If a homomorphically encrypted mind (with no decryption key) is conscious … it seems it knows things … that cannot be efficiently determined from physics.”
The move from “not P-efficiently determined from physics” to “mind exceeds physics (epistemically)” looks too strong. The same inferential template would force us into contradictions in ordinary physical cases where appearances are available to an observer but not efficiently reconstructible from the microphysical state.
Take a rainbow. Let p be the full microphysical state of the atmosphere and EM field, and let a be the appearance of the rainbow to an observer. The observer trivially “knows” a. Yet from p, even a quantum-bounded “Laplace’s demon” cannot, in general, P-efficiently compute the precise phenomenal structure of that appearance. The appearance does not therefore “exceed physics.”
If we accepted your step 10’s principle "facts accessible to a system but P-intractable to compute from p outrun physics" we would have to say the same about rainbows:
the rainbow’s appearance to an observer “knows something” physics can’t efficiently determine.
That is an implausible conclusion. The physical state fully fixes the appearance; what fails is only efficient external reconstruction, not physical determination.
Homomorphic encryption sharpens the asymmetry between internal access and external decipherability, but it does not introduce a new ontological gap.
So I agree with the earlier steps (digital consciousness, key distance irrelevance) but think the “mind exceeds physics (epistemically)” inference is a category error: it treats P-efficient reconstructability as a criterion for physical determination. If we reject that criterion in the rainbow case, we should reject it in the homomorphic case too.
Take a rainbow. Let p be the full microphysical state of the atmosphere and EM field, and let a be the appearance of the rainbow to an observer. The observer trivially “knows” a. Yet from p, even a quantum-bounded “Laplace’s demon” cannot, in general, P-efficiently compute the precise phenomenal structure of that appearance.
This may be true but it's really not obvious. The homomorphic encryption example makes one encounter such a case more clearly. If there's no hard encryption there, why couldn't Laplace's demon determine it efficiently?
That is an implausible conclusion. The physical state fully fixes the appearance; what fails is only efficient external reconstruction, not physical determination.
The thing you quoted and said was implausible had "efficiently" in it...
Homomorphic encryption sharpens the asymmetry between internal access and external decipherability, but it does not introduce a new ontological gap.
Yeah it just makes an existing problem more obvious.
At the end of the day the natural supervenience relation of observations on physics should work similarly in the rainbow case and the homomorphic encryption case. The homomorphic encryption case just makes more clear something that might have gotten skipped over in the rainbow case, "the natural supervenience relation need not be efficiently computable from the physical state; the information of the observations doesn't need to be directly sitting there, the way of picking it out might need to be a complicated function rather than a simple efficient 'location and extraction of information' one"
It seems you are biting the bullet and agreeing that the rainbow also has the problem of how a mind can be aware of it when it isn't (efficiently) reconstructable. But then this seems to generalize to a lot, if not all, phenomena a mind can perceive. Doesn't this reduce that conception of a mind ad absurdum?
I'm saying efficient reconstructibility is unclear in the rainbow case, but that the same principles have to explain it and non-efficiently-reconstructible cases like homomorphic encryption. I don't take this as a reducio but as a trilemma, see step 11.
I'm worried we talk past each other.
You’re saying:
- efficient reconstructibility is unclear in the rainbow case,
- but whatever the right story is, it must handle both rainbow-like cases and the engineered homomorphic encryption case,
- and if some of those cases force non-efficient supervenience, then we face your trilemma.
That part I agree with.
The point I’ve been trying to get at is: Once the same issue arises for ordinary optical appearances, we’ve left behind the special stakes of step 10! Because in the rainbow case, we all seem to accept (but maybe you disagree):
- appearance is fully determined by physics,
- but the mapping from microphysics to appearance may be extremely messy or intractable for an external observer,
- and we don’t treat that as evidence that the visual appearance “exceeds physics.”
Or, if rainbow-style cases also fall under the trilemma, then the conclusion can’t be “mind exceeds physics." It would have to be the stronger and more surprising “appearances as such exceed physics” or “macrostructure in general exceeds physics.” That’s quite different from your original framing, which presents the homomorphic encryption case as demonstrating a distinctive epistemic excess of mind relative to physics.
and we don’t treat that as evidence that the visual appearance “exceeds physics.”
This is still something I'd disagree with? Like, it still seems notable that visual appearances aren't determined as an efficient function of physics. It suggests perhaps there is more to reality than physics, otherwise what are you seeing? "Appearances as such exceed physics" is not substantially different from what I mean as "mind exceeds physics". This seems like a minor semantic issue. Appearances are mental, so if appearances exceed physics than so does mind; I'm not meaning any strong statement like "mind, and only mind, exceeds physics".
If you generalize to optics, then it seems your condition for “exceeding physics” is “not efficiently readable from the microstate,” i.e.X is not a P-efficient function of the physical state.”But then it seems everything interesting exceeds physics: biological structure, weather, economic patterns, chemical reactions, turbulence, evolutionary dynamics, and all nontrivial macrostructure. I'm sort of fine with calling this "beyond" physics in some intuitive sense, but I don't think that's what you mean. What work does this non-efficiency do?
It means reductionism isn't strictly true as ontology. I suppose it might be more precise to talk about "reductionist physics" than "physics", although some might consider that redundant.
It isn't obvious that biological structure isn't efficiently readable from microstate. It at least doesn't seem cryptographically hard, so polynomical time in general.
With turbulence you can pretty much read the current macrostate from the current microstate? You just can't predict the future well.
I'd say homomorphic encryption computation facts, not just mental ones, are beyond physics in this sense. Other macro facts might be but it's of course less clear.
Again, the same ontological status applies to homomorphic encryption and other entities. However the same epistemic status doesn't apply. And the "efficiently determinable" criterion is an epistemic one.
A reason to pay attention to mental ones is that they are more salient as "hard to deny the existence of from some perspectives". Whereas you could say a regular homomorphic encryption fact is "not real" in the sense of "not being there in the state of reality at the current time".
It means reductionism isn't strictly true as ontology.
I think you are working from an intuition of reductionism being wrong, but I'm still not clear about the details of your intuition. A defensible position could be that physics does not contain all the explanatorily relevant information or that reality has irreducible multi-level structure. But you seem to be saying that reductionism is false because subjective perspective is a fundamental ingredient, and you want to prove that via the efficiently computable argument. But I still think it doesn't work. First, it proves too much.
It isn't obvious that biological structure isn't efficiently readable from microstate.
Agree that it is not obvious.
Other macro facts might be but it's of course less clear.
But it seems pretty clear to me that most biological systems actually do involve dynamics that make it computationally infeasible for an external observer to reconstruct the macrostructure from microstructure observations at a given point. And we can’t appeal to ‘complete history’ to avoid the complexity, because with full history you could also recover the key in the HE case; the only difference is that HE compresses its relevant history into a small, opaque region.
What I do agree with you: Physics only tracks microstructure. But phenomenal awareness, meaning, macro-patterns, and information structure are not obviously reducible as descriptions to microstructure. The homomorphic case is a non-refutable illustration of this non-transparency.
But I disagree that this is caused by a failure of efficient computability; instead, we can see it as a failure of microphysical description to exhaust ontology. This matters because inefficiency is an epistemic constraint on observers, while ontology is about what needs to be included in the description of the world.
A defensible position could be that physics does not contain all the explanatorily relevant information or that reality has irreducible multi-level structure.
Close to what I mean. The multi-level structure is irreducible in that (a) it can't be efficiently computed from microstates (b) it is in some cases observable, indicating it's real. (Just (a) would be unsurprising, e.g. "the firth nth digits of Chaitin's omega where n is the number of atoms in a table" is a high-level physical property that is not computable from microstate.)
But you seem to be saying that reductionism is false because subjective perspective is a fundamental ingredient
That's not the claim. My argument wouldn't work if in all cases, subjective perceptions could be efficiently computed from microstates. And it is possible for subjective perceptions to be efficiently computed from microstates without subjective perceptions being a "fundamental ingredient". Rather I am vaguely suggesting something like neutral monism, where there is some fundamental ingredient explaining the physics lens and the mind lens.
But it seems pretty clear to me that most biological systems actually do involve dynamics that make it computationally infeasible for an external observer to reconstruct the macrostructure from microstructure observations at a given point.
It depends what kind of external observer you imagine right? Like if somehow we had a scan of a small animal down to the cellular level, there would be ordinary difficulties in re-constructing the macro-scale features from it, but none of them are clearly computationally hard (super-polynomial time).
But I disagree that this is caused by a failure of efficient computability; instead, we can see it as a failure of microphysical description to exhaust ontology. This matters because inefficiency is an epistemic constraint on observers, while ontology is about what needs to be included in the description of the world.
It seems like I entirely agree, not sure if I understood wrong. That is, I think path (c) is reasonably likely, and what it is saying is that there is more ontology than microphysics. It would be unsurprising for this to be the case, due to the way microphysical ontology, as methodology, is ok with dropping things that can be "in principle reconstrtucted", hence tending towards the microscopic layer (as everything can be "in principle reconstructed" from there); ignoring computational costs to doing so, hence plausibly dropping things that are actually real from the ontology.
I agree with J Bostock. I see no problem with A. Why do you think that polynomial complexity is this important?
(Thanks for a very nice structuring, btw!)
Speed prior type reasons. Like, a basic intuition is "my experiences are being produced somehow, by some process". Speed prior leads to "this process is at least somewhat efficient".
Like, usually if you see a hard computation being done (e.g. mining bitcoin), you would assume it happened somewhere. If one's experiences are produced by some process, and that process is computationally hard, it raises the question "is the computation happening somewhere?"
Informally, every possible physical state has a unique corresponding mental state. Formally:
My first pass response to this is: Yes, there's a unique mental state for each physical state, but the aspects of that mental state can be partitioned from each other in ways that are computationally intractable to un-partition. The mapping you use from raw physics or reality to whatever understanding you use it for[1] is a function not a primitive, and in this case that function could place you on either side of an informational partition[2] (depending on whether the mapping function does something like encrypts your viewing portal/perspective). Analogous to looking at an object from different perspectives, which under normal circumstances would be connectable efficiently, but here aren't.
Normally you can just privilege the simpler mapping function and get everything you'd want, but your simple mapping function isn't physics, it's viewing physics from a direction that looks simpler to you. If this is right:
- A misses that the homomorphic mind is 'real' from a different perspective, there's just more than one direction to be omniscient into the universe from
- The somewhat shaky assumptions B makes aren't required
- I don't quite think C's framing fits, it's not that reality exceeds physics, it's that physics isn't informationally/computationally interconnected in a way that makes any single perspective capable of efficiently getting all the interesting information.
I think some of Wolfram's work on the Ruliad gave me some of the intuitions I'm using here, if this feels worth digging into.
Right so, by step 4 I'm not trying to assume that h is computationally tractable; the homomorphic case goes to show that it's probably not in general.
With respect to C, perhaps I'm not verbally expressing it that well, but the thing you are thinking of, where there is some omniscient perspective that includes "more than" just the low level of physics (where the "more than" could be certain informational/computational interconnections) would be an instance. Something like, "there is a way to construct an omniscient perspective, it just isn't going to be straightforwardly derivable from the physical state".
Yeah, I think I model that anything which does understanding of physics is to some extent 'beyond physics', because you're translating from a raw file format to high level picture, and that's taking computation. Reading from the homomorphic one isn't an entirely new step, as opposed to the 'straightforward' one, it's just a much more difficult function in the place a usually simple function goes.
Or to take another shot: Yes to "there is a way to construct an omniscient perspective, it just isn't going to be straightforwardly derivable from the physical state"
However, I see 'straightforwardly' -> 'computationally intractable' as a difficulty jump for extracting high level features. It's a ~quantitive step up in the difficulty of an existing step of universe-parsing, not a novel step with strong metaphysical surprise.
Or to put it even more succinctly; if your omniscience isn't computationally unbounded omniscience, yeah, you're not going to be able to perceive things behind intractable computational boundaries. Omniscience is only as good as the perceiver.
Thanks for the link to Wolfram's work. I listened to an interview with him on Lex I think, and wasn't inspired to investigate further. However what you have provided does seem worthwhile looking into.
There's no need to drag consciousness and all its metaphysical baggage through all this. Consider instead a simulation of an environment, and a simulated robot in that environment which has sensors and has basic logical reasoning about what it senses, thereby allowing it to "know" various facts about its local environment.
I think then that step 4 is not strictly true. With the robot, M now just refers to its sensory states. I expect that there are many ways to come up with g/h such that the right sort of correspondence is satisfied. But taking into account the k-complexity of g/h allows such a grounding in-practice.
Similarly, it seems clear you could concoct a cursed g/h in this case such that 11.A is true. And the k-complexity is again what keeps you from needing to worry about these.
To be clear I am mainly talking about doxastic states, it's just that much of the past discussion and accordingly intuitions and terminology is based on "consciousness".
Step 4 is assuming that there are real f/g/h, which need not be known. I get that this might not be valid if there is fundamental indeterminacy. However even in that case the indeterminacy might decompose into a disjunction over some equivalence class of f/g/h triples?
For particular f/g it seems for natural supervenience to not hold would require extra-physical information, "antennae theory" or something. In the Chalmers sense I mean f/g to determine psycho-physical bridging laws which are sufficient for natural supervenience, so there is no extra "soul goo". So that the possible indeterminacy of the computational interpretation is fixed by deciding f/g.
I think basically g/h are part of an agent's anthropic priors. It builds a model of reality and of its state of mind, and has a distribution over ways to bridge these. I don't know what it would mean for there to be canonical such functions even in principle.
g/h can be posited by an agent e.g. Solomonoff induction.
But also, if you're talking about agents in the first place as meaningful things, then it seems something like "doxastic mental states" is already reified, in which case you can ask things like "do these supervene on the same reality physics does"... It doesn't really work to explain doxastic states in terms of other doxastic states in an infinite regress.
Sure.
I reject that there is any such "base ground" from which to define things. An agent has to start with itself as it understands itself. My own talk of agents is grounded in my own subjective experience and sense of meaning ultimately. Even if there was some completely objective one I would still have to start from this place in order to evaluate and accept it.
In practice it all ends up pretty normal. Everyone agrees on what is real for basically the same reason that any bounded agent has to agree on the temperature, even though it's technically subjective. The k-complexity priors are very constraining.
Well that seems like a good starting point. I guess then, some of the arguments could be subjectivized at the level of, among agents who believe they exist in reality, what possible hypotheses could they have about their mental states and reality and how they relate; is there something like a "disjunction over plausible alternatives" (which would include something like f/g), natural supervenience, etc. Then with k-complexity epistemology it's possible to ask, what sort of reality theory will that tend to produce, e.g. what would a k-complexity epistemology think about homomorphic encryption, in the case of other agents or itself? One thing I am suggesting is that computation bounded k-complexity type reasoning (speed prior etc) will tend to believe reality contains more information than micro-scale physics, as such information would otherwise be intractable (would be penalized by speed prior). Or put another way, physicalist reductionism "works" for computation-unbounded agents (given supervenience, information about microstates exhausts information about macrostates), but not computation-bounded agents (the derivation of macrostates from microstates is sometimes computationally intractable; this is extra relevant when such macrostates are observable, e.g. in the case of the homomorphically encrypted agent observing its own beliefs).
If minds can be encrypted, doesn't that mean that any bit string in a computer encodes all possible mind states, since for any given interpretation there's an encoding where it holds?
Forgive me, I'm probably being stupid again 😬.
On efficient computability being necessary for reality: I'm not sure I understand the logic behind this. Would you not always get diagonalization problems if you want supervening "real" things to be blessed with R-efficiently computability? For example, take R to be something like a Solomonoff induction. R-efficiently computable there means Turing computable. For our M which supervenes on R, instead of Minds, let's let M be the probability p of a given state. The mapping function g: R->M, mapping states to the probability of states, cannot be R-efficiently computed (no matter what sort of Turing machine or speed prior you use for R) for diagonalization reasons. So the probabilities of states aren't a "real" thing? It seems like a lot of natural emergent things wouldn't be R-efficiently computable.
On homomorphic encryption being un-reversible: quantum computers are reversible, right? So if you say physics is as powerful as a quantum computer, and you want homomorphic encryption to be uncomputable in polynomial time, you have to make P's physics "state" throw quantum information away over time (which it could, in e.g. Copenhagen or objective collapse interpretations, but does not in e.g. many worlds) or maybe restrict the size of the physical universe you're giving as state to not include information we radiated away many years ago (less than 62.9 billion light years).
(Don't feel obligated to reply)
Hmm... I think with Solomonoff induction I would say R is the UTM input, plus the entire execution trace/trajectory. Then M would be like the agent's observations, which are a simple function of R.
I see that we can't have all "real" things being R-efficiently computable. But the thing about doxastic states is, some agent has access to them, so it seems like from their perspective, they are "effective", being "produced somewhere"... so I infer they are probably "computed in reality" in some sense (although that's not entirely clear). They have access to their beliefs/observations in a more direct way than they have access to probabilities.
With respect to reversibility: The way I was thinking about it was that when the key is erased, it's erased really far away. Then the heat from the key gets distributed somehow. Like the information could even enter a black hole. Then there would be no way to retrieve it. (Shouldn't matter too much anyway if natural supervenience is local, then mental states couldn't be affected by far away physical states anyway)
Here's a pure quantum, information theoretic, no computability assumptions version that might or might not be illustrative. I don't actually know if the quantum computer I'm talking about could be built -- I'm going off intuition. EDIT I think this is 2 party quantum computation and none of the methods I've found are quite as strong as what I list here (real methods require e.g. a number of entangled qbits on order of the size of the computation).
You have two quantum computers, Alice and Bob, preforming the same computation steps. Alice and Bob have entangled qbits. If you observe the qbits of either Alice or Bob in isolation, you'll forever get provably random noise from both of them. But if you bring Alice and Bob together and line up their qbits and something something mumble, you get a pure state and can read off their joint computation.
Now we have all sorts of fun thought experiments. You run Alice and Bob, separating them very far from one another. Is Alice currently running a mind computation? Provably not, if someone looked at Bob last year. But Bob is many many light years away -- how can we know if someone looked at Bob? What if we separate Alice and Bob past each other's cosmic horizons, such that the acceleration of the expanding universe makes it impossible for them to ever reach each other again even if they run towards each other at the speed of light? Or send Bob to Alpha Centauri and back at close to the speed of light so he's aged only 1 year where Alice has aged 8. Has Alice been doing the mind thing for the past 7 years? Depends on whether you look at Bob or not.
(but I'll note that for me, this version, like the homomorphic version, is mostly saying that your description of a quantum physics state shouldn't be purely local. A purely local description must discard information, something something mixed state Von Neumann entropy)
Yeah that seems like a case where non-locality is essential to the computation itself. I'm not sure how the "provably random noise from both" would work though. Like, it is possible to represent some string as the xor of two different strings, each of which are themselves uniformly random. But I don't know how to generalize that to computation in general.
I think some of the non locality is inherited from "no hidden variable theory". Like it might be local in MWI? I'm not sure.
This is an extremely cool line of argument. The first thing that has concretely advanced my understanding of consciousness in quite a while.
Brains are already, in effect, encrypted. That is, we don't know how they work. We can't trace the wiring in useful detail and see exactly how they produce some visible action, even things as simple as engaging in conversation or walking without falling over. (We don't know nothing at all, but we don't know enough by a long way.) The same applies to LLMs. We do know how LLMs are trained, but we do not know how the resulting LLM works. Their behaviours are encoded in their parameters and we have no decryption key.
Step 2 codifies objective existence of subjective states. But let's suppose that homomorphic computation can be decrypted in two ways: one is what we encoded and the output is something like "it feels real", other is a minimally conscious state that happened to exist when decoding with a different key and its output is a noisy grunt expressing dissatisfaction with the noisy environment. Should the second one be included in M?
It seems that g and h cannot be efficiently computable if we decide to include the second state into M. On the second thought, if we don't have a list of minds in R, we need to analyze all the (spatially localized?) subsets of R to decide which ones of them are conscious. Could it be done efficiently?
ETA: Also, how to codify subjective existence of subjective states?
I think if M isn't "really mental", like there is no world representation, it shouldn't be included in M. I'm guessing depending on the method of encryption, keys might be checkable. If they are not checkable there's a pigeonhole argument that almost all (short) keys would decrypt to noise. Idk if it's possible to "encrypt two minds at once" intentionally with homomorphic encryption.
And yeah, if there isn't a list of minds in R, then it's hard for g to be efficiently computable, as it would be a search. That's part of what makes homomorphically encrypted consciousness paradoxical, and what makes possibility C worth considering.
Regarding subjective existence of subjective states: I think if you codify subjective states then you can ask questions like "which subjective states believe other subjective states exist?". Since it is a belief similar to other beliefs.
When I said "subjective existence" I've meant some model where we don't need a list of minds or exhaustive search for minds to make them real. After all the brain has its own computing power and requiring additional compute or data to make subjective experiences associated with its computations real looks extraneous. Interactions of a mind with our world, on the other hand, seem crucial for our ability to determine its existence.
BTW, thank you for laying out all this in such detail. It makes reasoning much more focused.
I reject the first step.
Most posts on this site just seem to posit that there is some "stuff" called information which just exists "somewhere" that is independent of any reference frames. That you can reference a "state" whatever that means.
Consider the set of all possible states in which an observer is reading a page out of a book from the library of babel. Now take one of these states that corresponds to a mind within the library of babel. From its subjective point of view, it has information about its environment corresponding to the page that it is reading, yet the total information contained in the system is actually less than that of the single observer, which can be specified as the set of all possible observers reading a page from the library of babel.
So where is the information coming from? It is the self location of the observer that contains the information. All the information is contained in the reference frame, and this is the primary concern of all condundrums about consciousness. Fundamentally consciousness is about reference frames and the semantics of language.
I could continue making objections at every step, but to keep things brief I will make only an objection which may bear some useful fruit, which occurs at step 5, that is the possibility of digital consciousness. I object to this step in the sense that a digital consciousness means an ability to copy or clone a system "perfectly" with digital accuracy. Again, the problem here is the relationship between reference frames and the ability to copy information. I posit that copying information is forbidden in the sense that you cannot copy reference frames. You run into the usual paradoxes around teleportation and sleeping beauty problems.
In physical reality the only way for an object to be copied is to be destroyed and instantiated somewhere else, and I posit this is how objects actually move through space. Motion is possible because it is impossible to make a digital copy of that object. If you allow for a digital copy of reference frames, suddenly you could perceive all sorts of physical law violations from a subjective point of view, and you may argue this is possible because this happens all the time in dreams. But we enter a slippery slope here, as now we must question our very foundations of physical reality and how to make sense of it.
Forgive me, I only scanned.You're talking about exponentially unlikely physical states, like the kind where you disintegrate from location 1 and just by chance an identical copy of you appears in location 2 for no reason, or the thermodynamic arrow of time runs backwards, or states that encode a mind you can't decode without the right homomorphic key but then the homomorphic key appears in your alphabet soup just by chance, or your whole life was an elaborate prank for a reality TV show and most of the universe is actually made of cheese, or there's a giant superintelligent pink elephant in every room but just by chance nobody notices them, or the Easter Bunny and Harry Potter both appear and their magic works just by chance each time they try to use it (in a way conforming to the standard model), or whatever. These states with ≈0 measure might be theoretically possible but personally I don't put much stock in thought experiments about them?
EDIT still only scanned, but I think I misread the post. I (unconfidently) think the post is about if someone homomorphically encrypts a mind computation, then moves the information in the key past the cosmic event horizon of the expanding universe so the information in the key and the encrypted mind can never return together again. (Or are exponentially unlikely to). You can get an effect like this by e.g. burning the key and letting the infrared light of the fire escape to the blackness of the night sky.
[This comment is no longer endorsed by its author]
That only comes in in step 10. I agree it's somewhat suspect. The main reason to imagine these scenarios is temporal locality of natural supervenience. That is, I believe that an agent does not have mental access to the distant past except mediated by the recent past and the present. Any access implying mental states would have to make no behavioral difference, else physical causality would be contradicted. So the randomly generated key is a supporting intuition for temporal locality, and I agree it has problems, but I still think temporal locality is correct, otherwise there would be strange consequences about knowing about the distant past not mediated by the recent past.