In general, people have a sensible aversion to trading items that are incomparable—for a sequence of such trades can easily lead you to items you strictly disprefer.
I don't see why this is sensible, because such trades can also easily lead you to items that you strictly prefer.
Consider three further explanations (just made up by me, I'm not very familiar with the literature):
- You might say that this is a good heuristic because trades are often adversarially chosen, but that's less true when you're making the decision yourself—e.g. in this case, where you can choose to exchange or not, there's no external agent that's instigating the trade.
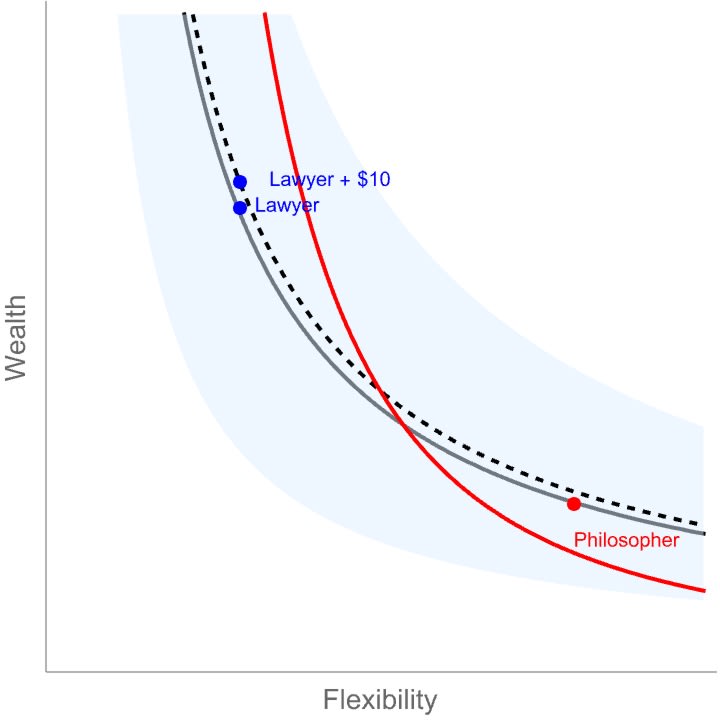
- You could see the endowment effect is an example of risk aversion. You have a gamecube in your hand, you can look at it, inspect it, and so on. Whereas the playstation is hypothetical, you don't know if it's going to be good, you don't even know if they're in stock, etc. But it seems like the classic examples of the endowment effect produce very little risk aversion because you literally have the two options right in front of you.
- Suppose you think of yourself as a multi-agent system, where different agents have different preferences over different features. You can then think of the choice between the two options as a negotiation between two factions, one of which prefers each. Negotiations generally rely on the choice of a "disagreement point". Before finding the GameCube, the most natural disagreement point is something like "choose between them randomly". But after finding the GameCube, the most natural disagreement point is "do nothing" aka "keep the GameCube".
This explanation in some sense just pushes the question back one step: why does the disagreement point change like this? But I think it might still be a useful frame. For example, it predicts that the endowment effect goes away (or perhaps even reverses) if you frame it as "we're going to swap them unless you object", so that now the "do nothing" disagreement point goes the other way.
Someone who you're likely to trade with (either because they offer you a trade or because they are around when you want to trade) are on average more experienced than you at trading. So trades available to you are disproportionately unfavorable and you cannot figure out which ones "are likely to lead to favorable trades in the future", by assumption that they are incomparable.
This is what you mean by "trades are often adversarialy chosen" in (1.), right? I don't understand why or in what situation you're dismissing that argument in (1.).
There can be a lot of other reasons to avoid incomparable trades. In accepting a trade where you don't clearly gain anything, you're taking a risk to be cheated and reveal information to others about your preferences, which can risk social embarrassment and might enable others to cheat you in the future. You're investing the mental effort to evaluate these things despite already having decided that you don't stand to gain anything.
An interesting counterexample are social contexts where trading is an established and central activity. For example, people who exchange certain collectibles. In such a context, people feel that the act of trading itself has positive value and thus will make incomparable trades.
I think this situation is somewhat analogous to betting. Most people (cultures?) are averse to betting in general. Risk aversion and the known danger of gambling addiction explains aversion to betting for money/valuables. However, many people also strongly dislike betting without stakes. In some social contexts (horse racing, LW) betting is encouraged, even between "incomparable options", where the odds correctly reflect your credence.
In such cases, most people seem to consider it impolite to answer an off-hand probability estimate by offering a bet. It is understood perhaps as questioning their credibility/competence/sincerity, or as an attempt to cheat them when betting for money. People will decline the bet but maintain their off-hand estimate. This might very well make sense, especially if they don't explicitly value "training to make good probability estimates", and perhaps for some of the same reasons as apply to trades?
I don't understand why or in what situation you're dismissing that argument in (1.).
Consider the specific example from the post: it's a store that has a longstanding policy of being willing to sell people items. There's almost no adversarial pressure from them: you know what's available, and it's purely your choice whether to swap or not. In other words, this is "a social context where trading is an established and central activity". So maybe we're just disagreeing on how common that is in general.
However, many people also strongly dislike betting without stakes.
Good point, I'll need to think about that.
Thanks, yeah I agree that this is a good place to press. A few thoughts:
- I agree with what Herb said below, especially about default aversion to trading especially in contexts where you have uncertainty
- I think you're totally right that those other explanations could play a role. I doubt the endowment effect has a single explanation, especially since manipulations of the experimental setup can induce big changes in effect sizes. So presumably the effect is the combination of a lot of factors—I didn't mean incomparability to be the only one, just one contributing factor.
- I think one way to make the point that we should expect less trading under incomparability is just to go back to the unspoken assumption economists were making about indifference. As far as I can tell (like I said in footnote 1), the argument that standard-econ models entail 50% trading ignores the possibility that people are indifferent, or assumes that if they are then still 50% of those who are indifferent will trade. The latter seems like a really bad assumption—presumably if you're indifferent, you'll stick with a salient default (why bother; you risk feeling foolish and more regret, etc). So I assume the reply is going to instead be that very few people will be PRECISELY indifferent—not nearly enough to lower the trading volume from 50% to 10%. And that might be right, if the only options are strict preference or indifference. But once we recognize incomparability, it seems pretty obvious to me that most people will look at the two options and sorta shrug their shoulders; "I could go either way, I don't really care". That is, most will treat the two as incomparable, and if in cases like this incomparability skews toward the default of not trading (which seems quite plausible in to me in thie case, irrespective of wheeling in some general decision theory for imprecise values), then we should expect way less than 50% trading.
What do you think?
presumably if you're indifferent, you'll stick with a salient default (why bother; you risk feeling foolish and more regret, etc).
I think this is assuming the phenomenon you want to explain. If we agree that there are benefits to not trading in general (e.g. less regret/foolishness if it goes wrong), then we should expect that the benefits will outweigh the benefits of trading not just when you're precisely indifferent, but also when you have small preferences between them (it would be bizarre if people's choices were highly discontinuous in that way). So then you don't need to appeal to incomparability at all.
So then the salient question becomes: why would not trading be a "salient default" at all? If you think about it just in terms of actions, there are many cases where it's just as easy as trading (e.g. IIRC the endowment effect still applies even when you're not physically in possession of either good yet, and so where trading vs not would just be the difference between saying "yes" and "no"). But at least conceptually trading feels like an action and not trading feels like inaction.
So then the question I'm curious about becomes "does the endowment effect apply when the default option is to trade, i.e. when trading feels like inaction and not trading feels like action?" E.g. when the experimenter says "I'm going to trade unless you object". That would help distinguish between "people get attached to things they already have" vs "people just go with whatever option is most salient in their mind", i.e. if it's really about the endowment or just inaction bias.
Yeah, I think it's a good question how much of a role some sort of salient default is doing. In general ("status quo bias") people do have a preference for default choices, and this is of course generally reasonable since "X is the default option" is generally evidence that most people prefer X. (If they didn't, the people setting the defaults should change it!). So that phenomenon clearly exists, and seems like it'd help explain the effect.
I don't know much empirical literature off-hand looking at variants like you're thinking of, but I imagine some similar things exist. People who trade more regularly definitely exhibit the endowment effect less. Likewise, if you manipulate whether you tell the person they're receiving a "gift" vs less-intentionally winding up with a mug, that affects how many people trade. So that fits with your picture.
In general, I don't think the explanations here are really competing. There obviously are all sorts of factors that go into the endowment effect—it's clearly not some fundamental feature of decision making (especially when you notice all the modulators of it that have been found), but rather something that comes out of particular contexts. Even with salience and default effects driving some of it, incomparability will exacerbate it—certainly in the valuation paradigm, for the reasons I mentioned in the post, and even if the exchange paradigm because it will widen the set of people for whom other features (like defaults, aversion to trade, etc.) kick in to prevent them from trading.
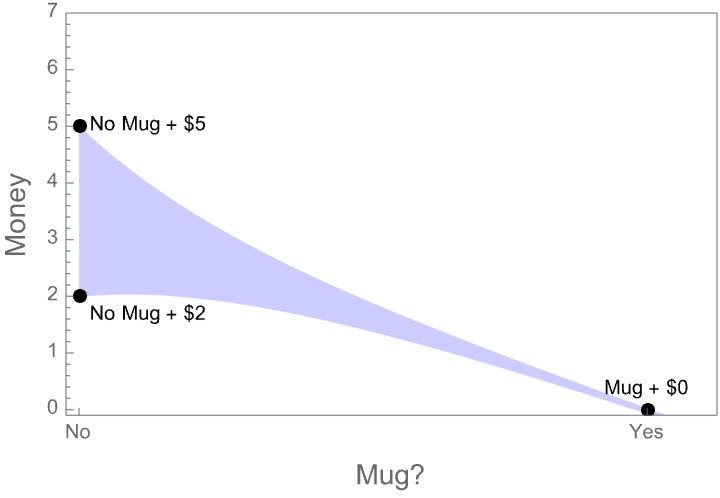
I'm confused by the pens and mugs example. Sure if only 10 of the people who got mugs would prefer a pen, then that means that at most ten trades should happen—once the ten mug-receiving pen-likers trade, there won't be any other mug-owners willing to trade? so don't you get 20 people trading, 20%, not 50%?
Not sure I totally follow, but does this help? Suppose it's true that 10 of 50 people who got mugs prefer the pen, so 20% of them prefer the pen. Since assignments were randomized, we should also expect 10 of 50 (20% of) people who got pens to prefer the pens. That means that the other 40 pen-receivers prefer mugs, so those 40 will trade too. Then we have 10 mugs-to-pens trades + 40 pens-to-mugs trades, for a total of 50 of 100 trades.
Thanksgiving break, early 2000s. A hectic time in the Dorst household. Grandparents are in town. The oversized puppy threatens books, lamps, and (he thinks) squirrels. There are meals to make, grandparents to impress, children to manage.
But most important—at least, according to said children—a decision must be made:
PlayStation 2 or GameCube?
We’d read the reviews, perused the games, and written pro/con lists. Though torn, we had a tentative verdict: PlayStation. It was cooler, faster, more “mature”.
Then, while casually strolling through my parents’ closet (as one does, during the holidays), I noticed a box. A GameCube box. Uh oh. It wasn’t too late. There was time yet to orchestrate an exchange—to get a cooler, faster, more mature console.
We didn’t. After all (we quickly concluded), the GameCube had better games, nicer controllers, and was more fun than the PlayStation, anyways. Thank goodness they got the GameCube!
This is an instance of what economists call the endowment effect: owning an item makes people value it more.
It’s one of the key findings that motivated the rise of behavioral economics, for it’s difficult to explain using standard economic models. Those models assume complete, stable preferences between options—meaning that if you prefer a PlayStation to a GameCube, then owning the latter shouldn’t change that.
There’s been a spirited debate about the causes of the endowment effect, but many proposals on the table assume that it’s in some way irrational.
My proposal: The endowment effect might be due to the fact that—unlike standard economic models—most real-world decisions are rife with incomparability: neither option is better than the other, but nor are they precisely equally good.
This idea is independently motivated, and offers a simple explanation of some of the main empirical evidence.
The Empirical Evidence
There are two main type of experiments supporting the endowment effect.
First, the valuation paradigm. Half of our subjects are randomly assigned as “buyers”, the rest as “sellers”. An item—say, a university-branded coffee mug—is presented. Buyers are simply shown it, while sellers are given it.
Buyers are asked how much money they’d be willing to pay (WTP) to buy the mug. Sellers are asked how much money they’d be willing to accept (WTA) to sell the mug.
The result? Buyers are willing to pay less—way less—than sellers are willing to accept. In the classic study, the buyers’ median WTP was $2.25, while the sellers’ median WTA was around $5.
Why think this is irrational? Standard models say that there’s a precise degree to which you value any option (its “utility”), represented as a real number. Utility creates a common currency amongst your preferences, allowing us to translate between how much you value an option and how much you value a corresponding amount of money.
Since the two groups were statistically indistinguishable, there should’ve been no average difference between how much each group valued the mug. As a result, the WTP and WTA should’ve been the same. The fact that they’re not—what’s known as the “WTP-WTA gap”—suggests that how much you value a coffee mug depends on whether or not you’ve owned it for the last two minutes.
Next, the exchange paradigm: randomly give half of our subjects mugs and half of them pens, then give each a chance to trade their item for the alternative.
Standard theory predicts that 50% of people should trade. After all, some proportion—say, 80%—will prefer mugs to pens, with the rest (20%) preferring pens to mugs.[1]
Since subjects were randomized, this proportion should be the same between the mug-receivers and pen-receivers. Now suppose there were 100 total subjects; 50 pen-receivers and 50 mug-receivers. Then 80% of the former group will trade (40 people), and 20% of the latter will trade (10 people), for a total of 50 of 100 people trading. Obviously the reasoning generalizes.
So 50% of people should trade. But they don’t. Instead, around 10% of people traded the item they were given.
There have been many empirical follow-ups delineating the ins and outs of the endowment effect, but these two experiments are the core pieces of evidence in its favor.
Incomparability
There are a lot of reasonable processes that can generate the endowment effect—for example, salience, attachment, or the informational and social value of gift-giving.
But let’s focus on one that economists seem to[2] have largely overlooked: values are often incompletely comparable.
Most economic models assume that rational people have precise values, represented with a real-valued utility function. Most philosophers think this is a mistake: attention to our actual patterns of valuing suggests that many options can’t be precisely ranked on a common scale. Moreover, there are (multiple) sensible decision theories for how to act in the face of such incomparability.
Example: you’re deciding between a career as a lawyer or a philosopher. The clock is ticking: you have to decide today whether to sign up for the LSAT or the GRE. (You can’t do both.)
You’re torn—you have no clear preference. Yet neither are you indifferent between the two. If you were indifferent, then “mildly sweetening” one of the options would lead you to prefer it. Compare: if you’re indifferent between chocolate and vanilla ice cream, and I offer you $10 to try the vanilla, you’ll happily do so.
Not so when it comes to careers: if you found out that the LSAT is $10 cheaper than you thought, you would still be torn between career choices.
Why? Like most things, the value of a career depends on multiple parameters—wealth and flexibility, say. And there is simply no precise exchange-rate between the two: no fact of the matter about precisely how much wealth an extra day-per-week of flexibility is (or should be) worth to you. Instead, there’s a range of sensible exchange rates. As a result, adding $10 to one option doesn’t determinately make it better.
For example, here’s a plot displaying how you are (rationally) disposed to trade off wealth and flexibility. Standard models require you to adopt a precise tradeoff, represented by one of the below curves—you’re indifferent between things on the same curve—since they exactly match your precise tradeoff between wealth and flexibility—and you strictly prefer anything above the curve to anything below the curve. So if you’re precisely indifferent between Lawyer and Philosopher, then you strictly prefer Lawyer+$10 to Philosopher:
But that’s nuts. Any such curve is overly precise. Your preferences between wealth and flexibility can at best be represented with a range of exchange-rates—any that can be drawn through the blue region, say. All agree that Lawyer+$10 is preferable to Lawyer, since it improves on wealth but leaves flexibility fixed. But they disagree on whether these options are better or worse than Philosopher—capturing the lack of comparability.
Notably, this failure of comparability between careers isn’t due to lack of information—the same point can be made with items that you have sentimental attachments to but no uncertainty about, like your wedding album vs. your prized faberge egg.
Compare fitness. Who was more fit in their prime: Michael Phelps or Eliod Kipchoge? There simply is no answer. Phelps had stronger arms. Kipchoge has (had?) legs of steel. And there is no precise “exchange rate” between arm strength and leg strength that creates a complete ordering of fitness. Life is rife with incomparabilities.
How to model them? Simple: just use a set of utility functions U—instead of a single one u—to represent your values. If you determinately prefer X to Y, then every u ∈ U assigns X higher value; if you determinately prefer Y to X, vice versa. But very often some u ∈ U will rank X above Y while another u’ ∈ U will rank Y above X—meaning that there is no determinate fact about which you prefer.
Notice what this means. If we try to translate how much you value such an option to a precise scale like money, the best we can do is determine a range of monetary values: the mug may be worth determinately more than $2, determinately less than $5, and yet it can be indeterminate whether it’s worth more or les than $3 or $4:
Explaining the Effect
Once we allow incomparability, we can easily explain the two main effects.
First, the valuation paradigm: when asked how much they’d be willing to pay (WTP) for a mug, people said around $2; but when asked how much they’d be willing to accept (WTA) in exchange for the mug, people said around $5.
The explanation is simple. If you ask me the most I’m willing to pay for a mug, I should only give you number if I know that I am willing to pay that much. So if it’s indeterminate whether I’d be happy to pay $3 for it, I should give a lower number (like $2) that I’d definitely be willing to pay.
Conversely, if you ask me the least I’d be willing to accept for the mug, I should again only give you a number if I know I am willing to accept. So if it’s indeterminate whether I’d be happy to accept $4 for it, I should give a higher number (like $5) that I definitely am willing to accept.
Compare this to a classic case of vagueness. If you ask me to pick the rightmost red patch, I’ll pick 2 since it’s not clear whether 3 is red; if you ask me to pick the leftmost yellow patch, I’ll pick 6 since it’s not clear whether 5 is yellow:
Upshot: the WTP-WTA gap is no more surprising than the rightmost-red/leftmost-yellow gap. Both may be due to vagueness.
Second, the exchange paradigm: when people are randomly given pens or mugs and then given the chance to exchange them for the alternative, only around 10% of people traded (rather than the predicted 50%).
The prediction that 50% of people would trade assumes either that people aren’t indifferent between the mug and the pen, or if they are indifferent then around 50% of those who are indifferent would trade on a whim.
But as we’ve seen, you should treat incomparable options differently than you treat options you’re indifferent between. In general, people have a sensible aversion to trading items that are incomparable—for a sequence of such trades can easily lead you to items you strictly disprefer.
The reason is that “X is incomparable to Y” is an intransitive relation. As we’ve seen, Lawyer+$10 is incomparable to Philosopher, and Philosopher is incomparable to Lawyer. But—obviously—Lawyer+$10 is strictly preferable to Lawyer. If you were willing to make trades between incomparable options, you could easily be led to trade Lawyer+$10 for Philosopher, and then trade Philosopher for Lawyer—leading you from one option to a strictly dispreferrable one.
As a result—absent special conditions—we should expect people to be averse to trading between options that are incomparable. Assuming the mug and pen are incomparable to some people, that lowers the proportion we should expect to trade below 50%. The only people who should trade are those who have a strict preference between the two and who got their dispreferred option.
Other Findings
This incomparability-based explanation fits with some of the other empirical findings around the endowment effect.
First, there is no WTP-WTA gap when people are trading tokens that have a precise exchange rate to money. This is what we should expect, since such tokens are fully comparable.
Second, the endowment effect is smaller for similar items. This makes sense: the more similar two items are, the more comparable they tend to be.
Third, experience trading the items reduces the endowment effect. Generally, we should expect that people who evaluate and trade a type of item regularly will come to be able to put more precise values on them—especially when such items are be evaluated on a precise metric (e.g. how much money you can make trading them). Thus experienced traders should have fewer incomparabilities in their preferences.
The upshot? Economists tend to ignore the possibility of incomparability in their models, yet it offers ready-to-hand explanations for some of the main data supporting the endowment effect. Of course, that’s not to say it can explain all those effects…
Back to the GameCube. Incomparability explains why my brother and I didn’t ask to trade the GameCube for a PlayStation—neither was strictly better than the other, in our eyes.
But it can’t explain the apparent rationalization we quickly did—concluding that the GameCube was far superior to a PlayStation. For that, we need another post on why—given incomparability—rationalization often maximizes expected value. Stay tuned.
What next?
Liked this post? Sign up for my Substack for more.
For more work by philosophers on incomparability, see this paper defending its possibility and this paper working out the decision theory.
For a different model of incomparability and its relevance to economics—tying it to Arrow’s impossibility theorem—see this interesting paper.
For a recent challenge to incomparability—but one for which uncertainty about values will play a similar role—see this paper.
As far as I can tell, the arguments that 50% of people will trade ignore the possibility of indifference. Presumably the (in my mind, questionable!) thought is either that few people will be precisely indifferent, or that amongst those who are, 50% of them will trade (on a whim?).
I’ve found no economists writing on this type of model—though see this paper for one similar in spirit—but I’m not an expert in this sub-area. If you know of more examples, please let me know!