This is a linkpost for https://outsidetheasylum.blog/understanding-subjective-probabilities/. It's intended as an introduction to practical Bayesian probability for those who are skeptical of the notion. I plan to keep the primary link up to date with improvements and corrections, but won't do the same with this LessWrong post, so see there for the most recent version.

Any time a controversial prediction about the future comes up, there's a type of interaction that's pretty much guaranteed to happen.

Alice: "I think this thing is 20% likely to occur."

Bob: "Huh? How could you know that. You just made that number up!".

Or in Twitterese:

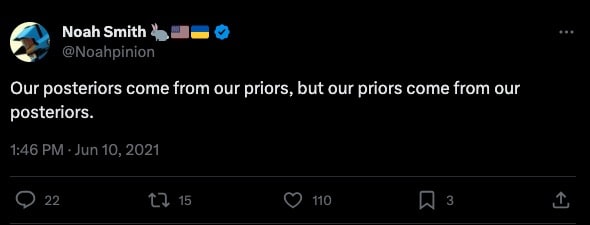
That is, any time someone attempts to provide a specific numerical probability on a future event, they'll inundated with claims that that number is meaningless. Is this true? Does it make sense to assign probabilities to things in the real world? If so, how do we calculate them?

Interpretations of probability

The traditional interpretation of probability is known as frequentist probability. Under this interpretation, items have some intrinsic "quality" of being some % likely to do one thing vs. another. For example, a coin has a fundamental probabilistic essence of being 50% likely to come up heads when flipped.

This is a useful mathematical abstraction, but it breaks down when applied to the real world. There's no fundamental "50% ness" to a real coin. Flip it the same way every time, and it will land the same way every time. Flip it without perfect regularity but with some measure of consistency, and you can get it to land heads more than 50% and less than 100% of the time. In fact, even coins flipped by people who are trying to make them 50/50 are actually biased towards the face that was up when they were flipped.

This intrinsic quality posited by frequentism doesn't exist in the real world; it's not encoded in any way by the atoms that make up a real coin, and our laws of physics don't have any room for such a thing. Our universe is deterministic, and if we know the starting conditions, the end result will be the same every time.^[1]

The solution is the Bayesian interpretation of probability. Probability isn't "about" the object in question, it's "about" the person making the statement. If I say that a coin is 50% likely to come up heads, that's me saying that I don't know the exact initial conditions of the coin well enough to have any meaningful knowledge of how it's going to land, and I can't distinguish between the two options. If I do have some information, such as having seen that it's being flipped by a very regular machine and has already come up heads 10 times in a row, then I can take that into account and know that it's more than 50% likely to come up heads on the next flip.^[2]

Dealing with "fuzzy" probabilities

That's all well and good, but how do we get a number on more complicated propositions? In the previous example, we know that the coin is >50% likely to come up heads, but is it 55%? 75%? 99%?

This is the hard part.

Sometimes there's a wealth of historical data, and you can rely on the base rate. This is what we do with coins; millions of them have been flipped, and about half have been heads and half are tails, so we can safely assume that future coins are likely to behave the same way.

The same goes even with much less data. There have only been ~50 US presidents, but about half have come from each political party, so we can safely assume that in a future election, each party will have around a 50% chance of winning. We can then modify this credence based on additional data, like that from polls.

How do we do that modification? In theory, by applying Bayes' rule. In practice, it's infeasible to calculate the exact number of bits of evidence provided by any given observation, so we rely on learned heuristics and world models instead; that is, we guess.

Guessing

It's obvious once you think about it for a moment that guessing is a valid way of generating probabilistic statements; we do it all the time.

Alice: "We're probably going to run out of butter by tonight, so I'm going to go to the grocery store."

Bob: "Preposterous! Have you been tracking our daily butter consumption rate for the past several weeks? Do you have a proven statistical model of the quantity of butter used in the production of each kind of meal? Anyway we just bought a new stove, so even if you did have such a model, it can no longer be considered valid under these new conditions. How would you even know what dinner we're going to make this evening; I haven't yet told you what I want! This is such nonsense for so many reasons, you can't possibly know our likelihood of running out of butter tonight."

Clearly Bob is being unreasonable here. Alice does not need a detailed formal model suitable for publishing in a scientific journal^[3]; she can draw on her general knowledge of how cooking works and her plans for the evening meal in order to draw a reasonable conclusion.

And these sorts of probabilistic judgements of the future are ubiquitous. A startup might try to guess what fraction of the population will use a new technology they're developing. A doctor might work out the odds of their patient dying, and the odds of each potential treatment, in order to know what to recommend. A country's military, when considering any action against another country, will estimate the chance of retaliation. Etc.

Probability words

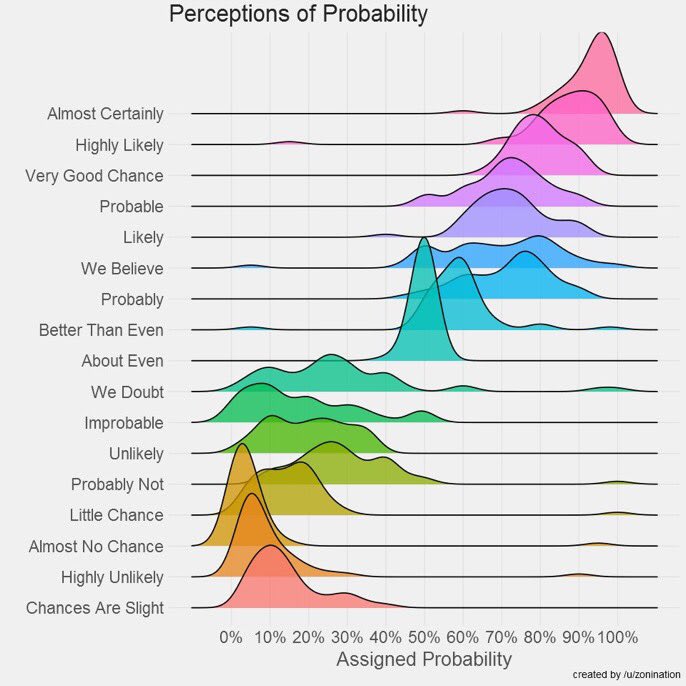
Does it matter that Alice said "probably" rather than assigning a specific number to it? Not at all. Verbal probabilities are shorthand for numerical ranges, as can be demonstrated by one of my all-time favorite graphs:

By u/zonination^[4]

We have to be careful though, since probability words are context-dependent. If my friend is driving down the highway at 140kph without wearing a seatbelt, I might tell them "hey, you're likely to die, maybe don't do that". Their actual probability of dying on a long trip like this is less than 0.1%, but it's high relative to a normal driver's chance, so I'm communicating that relative difference.

This is a very useful feature of probability words. If I say "nah, that's unlikely" then I'm communicating both "the probability is <50%" and "I think that probability in this context is too low to be relevant", which are two different statements. This is efficient, but it also greatly increases the chance of miscommunications, since the other person might disagree with my threshold for relevance, and if they do there's a huge difference between 1% and 10%. When precision is needed, a specific number is better.^[5]

Probabilities are no different from other units

Humans have a built-in way to sense temperature. We might say "this room is kind of warm", or "it's significantly colder than it was yesterday". But these measures are fuzzy, and different people could disagree on exact differences. So scientists formalized this concept as "degrees", and spent years trying to figure out exactly what it meant and how to measure it.

Humans don't naturally think in terms of degrees, or kilometers, or decibels; our brains fundamentally do not work that way. Nevertheless, some things are warmer, farther, and louder than others. These concepts started as human intuitions, and were slowly formalized as scientists figured out exactly what they meant and how they could be quantized.

Probabilities are the same. We don't yet understand how to measure them with as much precision as temperature or distance, but we've already nailed down quite a few details.

My subjective judgements about temperature are not precise, but that doesn't mean they're meaningless. As I type this sentence, I'm not sure if the room I'm sitting in is 21 degrees, 22, or maybe 23. But I'm pretty sure it's not 25, and I'm very sure it's not 15.^[6] In the same way, my subjective judgements about probability are fuzzy, but still convey information. I can't say with confidence whether my chance of getting my suitcase inspected by TSA the next time I fly is 25% or 35%, but I know it's not 1%.

Can precise numbers impart undue weight to people's claims?

Sure, they can. If someone says "it was exactly 22.835 degrees Centigrade at noon yesterday", we'd tend to assume they have some reason to believe that other than their gut feeling, and the same goes for probabilities. But "I'd be more comfortable if you lowered the temperature by about 2 degrees" is a perfectly reasonable statement, and "I think this is about 40% likely" is the same.

Since the science of probability is newer and less developed than the science of temperature, their usage in everyday life is less frequent. In our current society, even a vague statement like "around 40%" can be taken as implying that some sort of in-depth study has been performed. This is self-correcting. The more people normalize using numerical probabilities outside of formal scientific fields, the less exceptional they'll be, and the lower the chance of a misunderstanding. Someone has to take the first step.

More importantly, this criticism is fundamentally flawed, as it rests on the premise that bad actors will voluntarily choose not to mislead people. If someone has the goal of being trusted more than they know they should be, politely asking them not to do that is not going to accomplish anything. Encouraging people not to use numerical probabilities only harms good-faith dialog by making it harder for people to clearly communicate their beliefs; the bad actors will just come up with some bogus study or conveniently misunderstand a legit one and continue with their unearned confidence.

And encouraging people to never use numerical probabilities for subjective estimates is far worse. As the saying goes, it's easy to lie with statistics, but it's easier to lie without them. Letting people just say whatever they want removes any attempt at objectivity, whereas asking them to put numbers on their claims let us constrain the magnitude of the error and notice when something doesn't seem quite right.

On the contrary, very often (not always!), the people objecting to numerical probabilities are the ones acting in bad faith, as they try to sneak in their own extremely overconfident probabilistic judgements under the veneer of principled objection. It's not uncommon to see a claim along the lines of "How can you possibly know the risk of [action] is 20%? You can't. Therefore we should assume it's 0% and proceed as though there's no risk". This fails elementary school level reasoning; if your math teacher asks you to calculate a variable X, and you don't know how to do that or believe it can't be done with the information provided, you don't just get to pick your own preferred value! But under the guise of objecting to all numerical probabilities, the last sentence is generally left unsaid and only implied, which can easily trip people up if they're not familiar with the fallacy. Asking people to clearly state what they believe the probability to be prevents them from performing this sort of rhetorical sleight of hand, and provides a specific crux for further disagreement.

What does it mean to give a probability range?

In my experience, the people who use numerical probabilities are vastly more worried about accidentally misrepresenting their own level of confidence than the people who dislike numerical probabilities. A common way they do this is to give a probability range; rather than say "I'm 40% sure of this", they'll say "I think it's somewhere from 20% to 50% likely".

But what does this mean exactly? After all, a single probability is already a quantification of uncertainty; if they were sure of something, it'd just be 0% or 100%. Probability ranges seem philosophically confused.

XKCD

To some extent they are, but there's a potentially compelling defense. When we talk philosophically about Bayesian probability, we're considering an ideal reasoner who applies Bayes' theorem to each new bit of evidence in order to update their beliefs.^[7] But real humans are not this good at processing new information, and our behavior can substantially differ from that of a perfect reasoner.

So a probability range can be an attempt to communicate our expected level of error. If someone says "I think this is 20% to 50% likely", they mean something like "I'm 95% confident that an ideal Bayesian reasoner with the same information available to me would have a credence somewhere between 20% and 50%". Just like how one might say "I'm not sure exactly how hot it is in here, but I'm pretty sure it's somewhere from 19 to 23 degrees."

There's also another justification, which is that a probability range shows how far your probability might update given the most likely pieces of information you expect to encounter in the future. All probabilities are not created equal; the expected value of bets placed on your credences depends on how many bits of information that credence is based on. For example, your probability on a coin flip coming up heads should be 50%, and if someone offers to bet you on this at better odds, it's positive expected value to accept.

But now say someone offers a slightly different game, where they've hidden a coin under a cup, and you can bet on it being heads-up. Going into this game, your credence that it's heads will still be 50%, since you have no particular information about which face is up. But if the person offering the game offers you a bet on this, even a 2:1 bet that seems strongly in your favor, you should probably not accept, because the fact that they're offering you this bet is itself information that suggests it's probably tails.^[8] So giving a probability range of "30% to 70%" could mean something like "My current credence is 50%, but it seems very plausible that I get information that updates me to anywhere within that range." In other words, the width of the range represents the value of information for the most likely kinds of information that could be gained.^[9][10]

Both of these usages of probability ranges are fairly advanced, and can be ignored for everyday usages.

Making good estimates

Just like some experience measuring things will help you make better estimates of distance, some experience forecasting things will help you make better estimates of probability. People who want to be good at this generally practice by taking calibrated probability assessments^[11], competing in forecasting tournaments, and/or placing bets in prediction markets. These sorts of exercises help improve your calibration; your ability to accurately translate a vague feeling into a number.

For relatively unimportant everyday judgements, nothing more is needed. "Hey, are you going to be able to finish this project by tomorrow?" "Eh, 75%". But sometimes you might want more certainty than that, and there are a number of ways to improve our forecasts.

First, always consider the base rate. If you want to know how likely something is, look at how many time it's happened in the past, out of some class of similar situations. Want to know how likely you are to get into a car accident in your next year of driving? Just check the overall per-kilometer accident rate in your region.

Unfortunately, this can only get you so far before you're playing "reference class tennis"; unsure of what class of events counts as "similar enough" to make a good distribution. (Maybe you have strong evidence that you're a more reckless driver than average, in which case you'd want to adjust away from the base rate.) And when predicting future events that aren't very similar to past events, such as the impact of a new technology, there often is no useful reference class at all.

When this occurs, another option is to take heuristic judgements of which you're relatively confident and combine them together, following the axioms of probability, in order to derive the quantity you're unsure of. Maybe you were able to look up that a regular driver has a 0.1% chance of getting into an accident per year, and you know from personal experience that you tend to drive about 30% faster than the average. Now all you need to look up is the global relationship between speed and accident rate, and then you can calculate the probability you want to know.

Another option that can go hand in hand with the previous ones is to use several different methods to make multiple probability estimates, and compare them against each other. If they're wildly different, this is a hint that you've made an error somewhere, and you can use your specific knowledge of the system and your likely biases to try to figure out where that error is.

For example, when considering whether to trust "gut feelings" over explicit models, consider whether the situation is one that your brain's heuristics were designed for or trained on. If it's a situation similar to the ones that humans encountered frequently in the past million years, then natural selection will have made us reasonably good at estimating it. Or if it's a situation that you've encountered many times before, you've probably learned a good heuristic for it on an intuitive level. But if it's something that you and your ancestors would have been unfamiliar with, the explicit model is likely to be more reliable.

When you have multiple independently-obtained probability estimates, after adjusting them for the reliability of the method used to obtain them, take the geometric mean of the odds^[12] in order to collapse them down to a single number. This allows you to take advantage of the wisdom of crowds, without even needing a crowd.

1. ^{^}

   That's not quite true; quantum mechanics may have some fundamental randomness, if the Copenhagen interpretation is correct. But if the many-worlds interpretation or superdeterminism is true, then there's isn't. This also doesn't particularly matter, because as long as it's logically possible to conceptualize of a world that's deterministic, we'd need a theory of probability that works in that world.

2. ^{^}

   In fact you don't even need the knowledge that it's being flipped by a machine; seeing 10 heads in a row is enough to conclude that it's more than 50% likely to be heads again. If you had no prior knowledge of the coin at all, this could be determined by applying Laplace's Law of succession. With the knowledge that it looks like a normal coin, which are difficult to strongly manipulate, you'd want to adjust that towards 50%, but not all the way.

3. ^{^}

   And even these sorts of scientific models tend to contain a lot of assumptions that the researchers chose with the "guess based on experience" method.

4. ^{^}

   No I don't know why the last three are presented out of order, that bothers me too. Nor why some of the distributions go below 0% or above 100%. Probably just poor graph-design. There's a more rigorous investigation of this here, which finds similar results.

5. ^{^}

   An illustrative excerpt from The Precipice, in the section on catastrophic risk from climate change:
   
   "The IPCC says it is 'very unlikely that methane from clathrates will undergo catastrophic release (high confidence)'. This sounds reassuring, but in the official language of the IPCC, 'very unlikely' translates into a 1% to 10% chance, which then sounds extremely alarming. I don’t know what to make of this as the context suggests that it was meant to reassure.

6. ^{^}

   If you live in an uncivilized country like the United States, I'll leave the conversion to freedom units up to you.

7. ^{^}

   There are actually an infinite number of ideal reasoners who use different priors. But some priors are better than others, and for any reasonable prior, like computable approximations of a Solmonoff prior, will yield similar results once some real-world information is factored in.^[13] Probably. This is still an active area of study. If humanity knew all the answers here, we'd be able to create superintelligent AI that reasons in a mathematically optimal way and easily defeats humans at all prediction tasks, so it's probably good that we don't.

8. ^{^}

   This is the explanation for why it's often rational in a prediction market to only bet with a relatively large spread between YES and NO, rather than betting towards a single number.

9. ^{^}

   This is similar to putting a probability distribution over what probability you'd assign to the proposition if you were to spend an additional 1000 hours researching it, and then measuring the width of that distribution.

10. ^{^}

    It also helps resolve the optimizer's curse^[14]; if you're estimating probabilities for different options and picking the one with the highest expected value, you're likely to pick one where you overestimated a probability somewhere. Knowing the amount of information that went into each estimate allows you to skew towards the ones with a smaller range.

11. ^{^}

    You can try your hand at some free online exercises here.

12. ^{^}

    Not the geometric mean of the probabilities! Doing that would lead to invalid results, since for example the geometric mean of 0.1 and 0.2 is a different distance from 0.5 as the geometric mean of 0.8 and 0.9. You instead convert probabilities to an odds ratio first, like how 50% is 1:1 and 75% is 3:1.^[15] Then you take the geometric mean of the odds and convert that back to a probability.^[16]

13. ^{^}

    Of course we only believe that the Solmonoff Prior is in some sense "good" because of whatever priors evolution build humans with, which is itself somewhat arbitrary. So there's a sort of infinite regress where we can't actually talk about a fully optimal reasoner. But we can definitely do better than humans.

14. ^{^}

    A variant of the winner's curse

15. ^{^}

    Using fractional odds if necessary, so the second number is always 1. 25% under this system is 1/3:1.

16. ^{^}

    Here's a Wolfram Alpha link that will do it for you, just replace the values of "a" and "b" with the ends of your range.