[Crossposted on Windows In Theory]
 

“Modern humans first emerged about 100,000 years ago. For the next 99,800 years or so, nothing happened. Well, not quite nothing. There were wars, political intrigue, the invention of agriculture -- but none of that stuff had much effect on the quality of people's lives. Almost everyone lived on the modern equivalent of $400 to $600 a year, just above the subsistence level …  

Then -- just a couple of hundred years ago, maybe 10 generations -- people started getting richer. And richer and richer still. Per capita income, at least in the West, began to grow at the unprecedented rate of about three quarters of a percent per year. A couple of decades later, the same thing was happening around the world.”  Steven Lundsburg

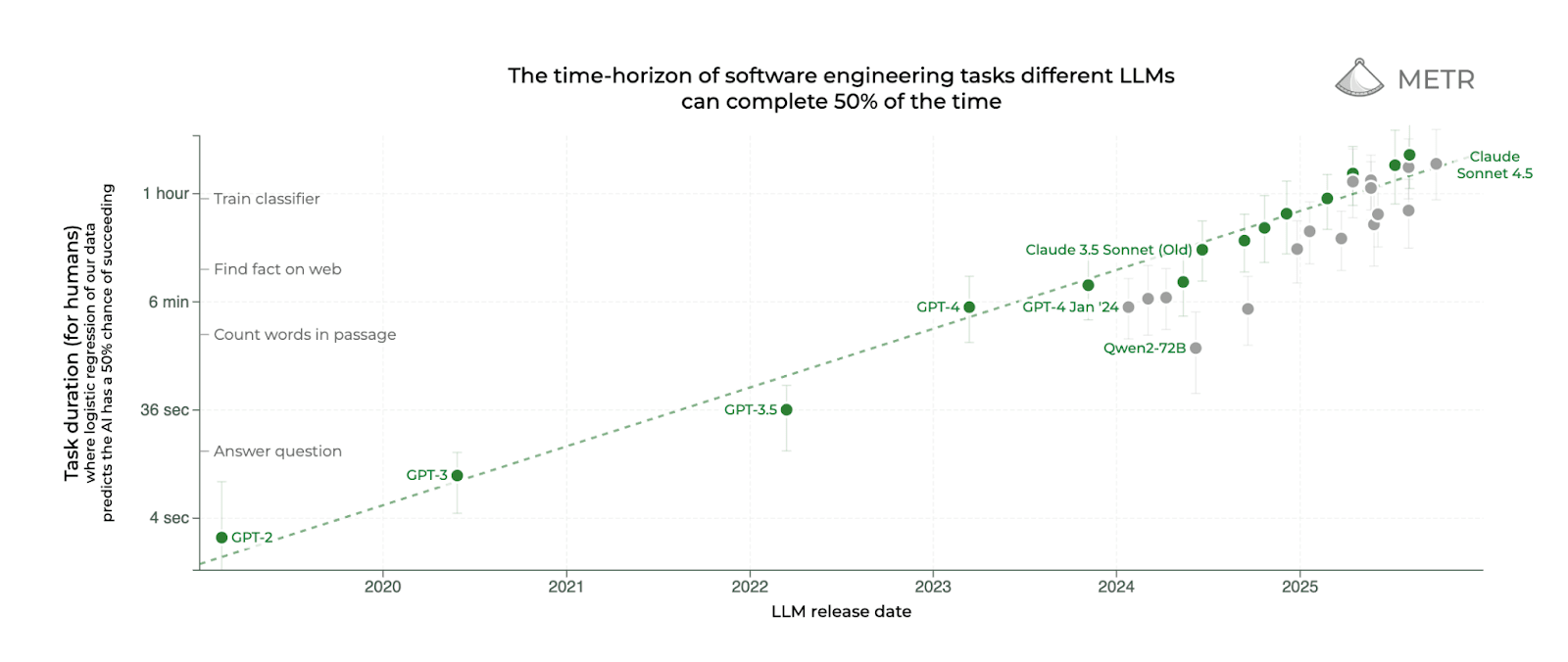
METR has had a very influential work by Kwa and West et al on measuring AI’s ability to complete long tasks. Its main result is the following remarkable graph:

On the X axis is the release date of flagship LLMs. On the Y axis is the following measure of their capabilities: take software-engineering tasks that these models can succeed in solving 50% of the time, and measure the time it takes humans to solve them.

While it is not surprising that models improve over time, the main reason this graph is remarkable is because the Y axis is on a log scale. This means that there is a fixed period of time after which models have doubled the length of tasks they can complete successfully. Specifically METR estimates this “doubling time” (which is proportional to the inverse of the slope of the line in this graph) at about 7 months, although they note that it may have accelerated recently (to as little as 3 months if considering only models after 2024). In this blog, just to make things simple, I will assume doubling time is 6 months, so the length of time horizon quadruples every year. (All numbers here are very rough.)

There are many factors that could potentially impact these results (and METR did a pretty admirable job of enumerating them). It is worth separating them into factors that impact the intercept (the actual length of time horizon of tasks that models can do) and factors that impact the slope (the doubling time) or possibly even the shape (e.g. breaking the linear relation between model release time and log horizon).

Factors impacting the intercept

The precise values — e.g., GPT5 doing tasks that take humans 2 hours and 17 minutes — could be impacted by numerous factors:
 

• Reliability factor (↓) - the graph is plotted at 50% reliability. For 80% reliability METR got a similar slope (that is about the same doubling time)  but the intercept is much lower, e.g. GPT5 can only perform tasks that take 26 minutes. (See also note on 100% accuracy below.)
   
• Task type (↕)- the graph is plotted for a specific benchmark. METR also studied other domains. The data is more sparse but broadly concurs with the straight line fit (sometimes an even steeper line, though some of these datapoints are only available for more recent models where the slope is steeper).
   

• “Benchmark bias” (↓)- AI models tend to do much better in tasks that are well scoped and easy to measure success in, while real world tasks are much “messier” - in their specification, the context needed to solve them, and the way we measure success. It is still an open question if this impacts only the intercept, also the slope, or even the shape of the curve. “Field experiments” are still very limited and with mixed results. However, the rapid rise in actual usage of AI is an indication that models’ capabilities are not just limited to lab setting.Personally I am sure that this has a significant impact on the “intercept” —  models pay a significant “messiness tax” in translating their performance from benchmarks to the real world — but I am not convinced it impacts the slope. That is, the “messiness tax” may well be a fixed constant c<1 multiplier on the duration of tasks that models can handle.

   

Factors impacting the slope/shape

• Exponential inputs (↓): The X axis of time for model release combines a number of inputs to models that have been growing at a rapid rate. These include compute, staff at AI labs, data, capital investment in AI, and more. For example Epoch AI estimates that the training compute for models has been doubling every 6 months. If the base of this exponent changes in one way or the other, this will likely impact the rate of progress. In particular, tautologically, sustaining exponential growth in inputs becomes exponentially more challenging over time–and quickly becomes impossible. That said, so far investment in these resources is showing no signs of slowing down.
  
   
• New data / active learning (↓): So far by and large LLMs have been training on data produced by humans. One comparison can be to a human student, who throughout K-12 and undergraduate studies mostly learns from textbooks - knowledge that has already been collected. However, in many professions, and in particular in science and inventions, humans need to discover new knowledge and collect new observations from the real world. If LLMs require inputs such as running scientific experiments or acting in the world to improve their intelligence, that would slow progress down. That said, so far we have not seen any such slowdown even as LLMs are becoming more “agentic”. Indeed, the METR data is only showing a speedup in the slope in recent years.
  
   
• Physical tasks and data (↓): METR primarily focused on software engineering. It is possible these trends will extend to other kinds of cognitive labor. But we do not know if they extend to domains where people need to either act in the physical world, or collect data from the physical world. While robotics has been advancing as well, it is unclear whether or not it follows a similar exponential curve. Even if state of the art robotics improve at a similar rate to state of art models, manufacturing robots at scale can remain a bottleneck.
  
  I personally do not believe in a “data wall.” I believe that there are diminishing returns to more data of the same type, and the advances over the last few years, as captured by the METR graph, have largely not been due to a larger quantity of data from the Internet. Also, while so far much of AI’s economic impact has been in software engineering, it is telling that the best models for software engineering are ones that are trained on very general data, and are often good at many other tasks (while this article is about Claude code,I can’t help but note that in my experience codex too is great for non-coding tasks :) ). In my view, thinking that AI’s impact would be restricted to software engineering is analogous to thinking in January 2020 that Covid’s impact would be restricted to China.
  
   
• Threshold effects (↑): These tasks are measured with respect to humans that have certain time scales in which they operate on. Us humans need to sleep, take breaks, and split work between workers, which requires isolating the context needed for completing a task and the way to measure its success. Hence we break tasks into ones that can be achieved in a working day, week, month, quarter. (I believe that even Andrew Wiles, who worked on Fermat’s last theorem for 7 years, broke it down to multiple intermediate results.) Thus it is possible that once AI reaches a certain time horizon, either (a) the measurement no longer makes sense, or (b) it can essentially simulate any combination of humans working for an arbitrarily large amount of time.
  
   
• Recursive self improvement (↑): An important input to the process of producing AI models has been the work of human researchers and engineers. If AI itself can produce that input, then it could correspond to a massive increase in this input. It is still unknown whether using AI for automating the AI creation process will lead to a singularity, increase in slope, one-time boost, or just help sustain the exponential.

The bottom line is that we have significant uncertainty about the intercept, but arguably less about the slope, or at least the general shape of it up to the point of recursive self improvement / full automation of all human cognitive labor. So from now on I will just assume that time horizons will be doubling every 6 months and make no assumptions about the actual values of the time horizons themselves.

Sigmoidal relationship

Another remarkable figure in the METR paper is the following (Figure 5 there):

What I find striking about it is how good is the “sigmoid fit” for the performance of models as a function of the time duration it takes a person to do the task. In particular it seems that there is a certain threshold of time duration such that below it, models essentially are successful 100% of the time. This suggests that even the “100% horizon” (as hard as it is to measure empirically) will also double at a similar rate.

One way to think about this relation is that each task has a notion of “difficulty” (captured by log horizon length) and models have a certain “skill” level that corresponds to how likely they are to succeed. In this sense, this is similar to the ELO scale - we can think of the log horizon as the “ELO rating” of the task, and a model will “win” against the task with 50% chance if it has the same ELO rating. (Thanks to Jacob Hilton for this analogy.) For what it's worth, here is the chess ELO rating of models over time (as well as of humans), which displays a similar linear growth over time (though with a long plateau from around 1997-2007).

Decreasing costs

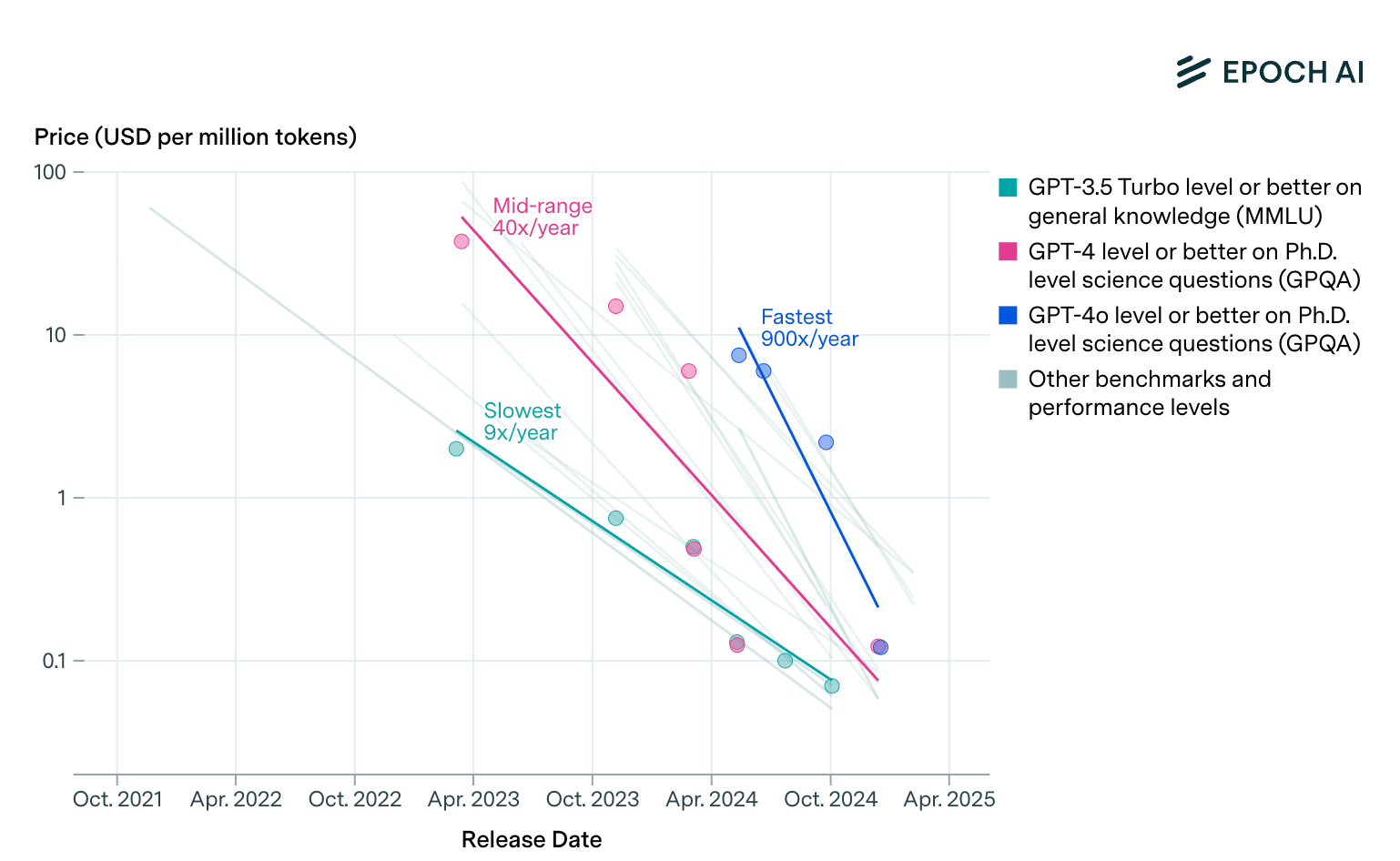
Another striking statistic has been the rapid reduction in prices for inference. That is, while it is often costly to extend the frontier of intelligence, once we achieve a certain level X, the cost to provide the same level has been decaying by factor 10x or more per year. It seems that once we reach a certain frontier the first time, it is much cheaper and easier to reach it for the second time (see also the “deepseek moment”). If this trend continues, it might mean that once a job is automated, within a year the cost for AI to do it will become insignificant. 

Discussions on AI often assume that robotics would be an exception, where we would not see as much progress. There are reasons to assume that due to costs of production, and the inability to deploy robots as flexibly as we can virtual AI assistants, costs for robotics would not be decreasing at the same rate. It is less clear to me that there is a fundamental reason that the “doubling time” - growth in complexity of tasks that robots can perform - would grow much slower than for other AI systems, but as far as I know there is no data on this point.

Implications for GDP growth

This is where I am getting to be pretty out of my depth, but I do want to see if there are ways to make back of the envelope calculations. Because I am focused on “slope” vs “intercept”, I will not try to predict so much when AI will lead to a certain growth but rather how fast we would get from the point of significant growth to explosive growth. For example, how many years would it take from the point that AI contributes to a 5% total growth in GDP to the point when due to AI GDP has doubled.

I am focusing in this post only on growth, and not considering employment outcomes. It is possible to construct some “knife edge” scenarios under which human displacement perfectly balances out productivity contributions of AI, leading to decreased employment without increase in growth. But I don’t believe such scenarios can be sustained under our assumptions of exponential growth in capability and decrease in costs. Hence, assuming above trends continue, significant labor impacts of AI will have to be coupled with significant productivity gains.

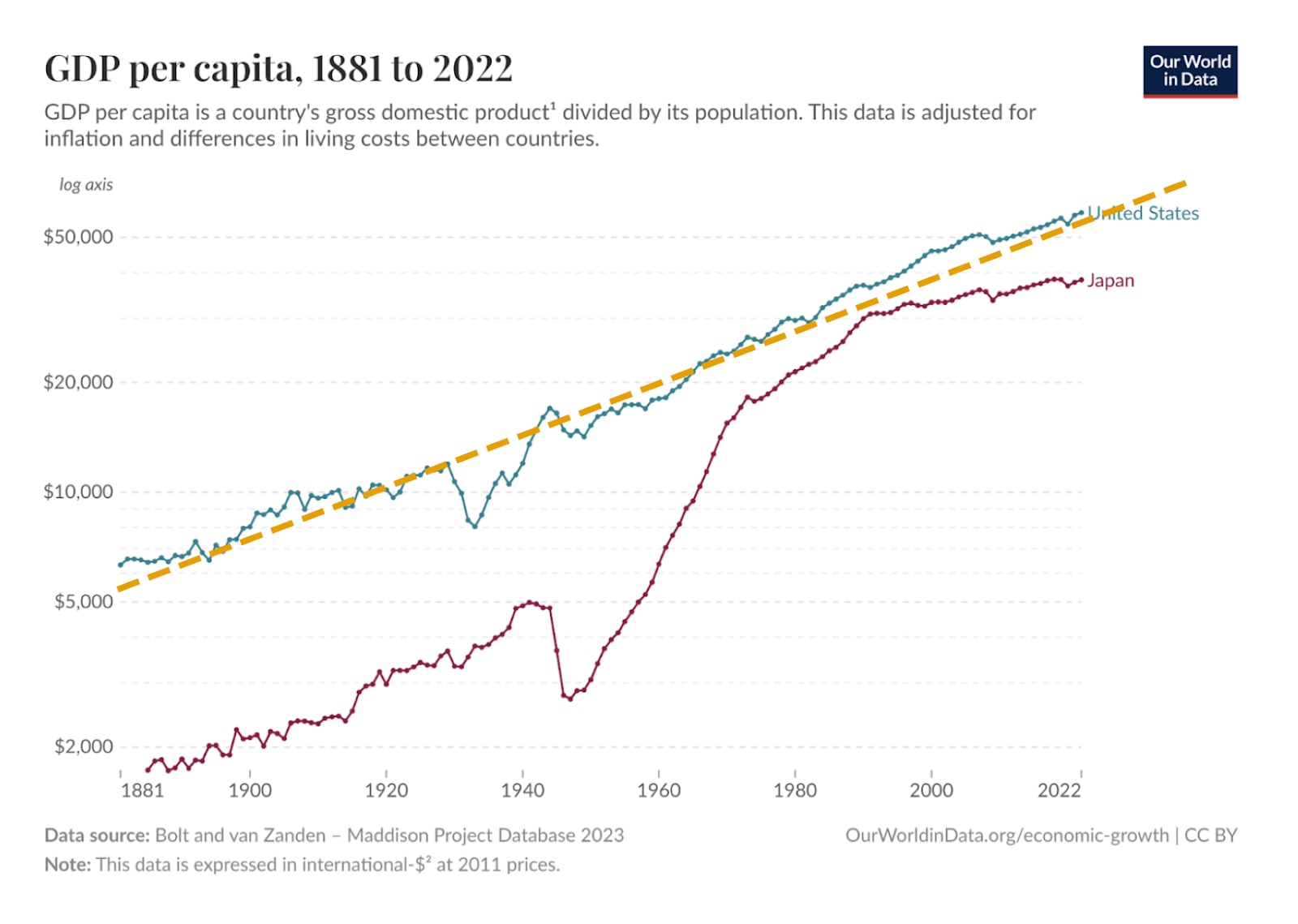
A remarkable fact is that (adjusted for inflation)  U.S. GDP per capita has been growing at essentially a constant rate of roughly 2% over the past 150 years. None of the inventions in this period— including electrification, internal combustion engine, computers and the Internet— changed this trajectory. Note that 2% growth corresponds to a GDP “doubling rate” of 35 years. 

Other countries have seen more significant fluctuations in growth (e.g. see Japan) though it seems that it is easier to grow at a rapid rate when you are far from the frontier, but once you reach it you slow down. This makes sense from the point of view that advancing the frontier requires inventing new ideas, while advancing to the frontier only requires copying and adapting existing ideas.

Still it is interesting that GDP growth has been only 2% (or maybe around 3% if we don’t consider per capita) even though Moore’s law corresponds to a growth rate of about 40% per year. One explanation is “Baumol’s cost disease” - while computers have been getting far more productive, people have been the bottleneck (see also section II.C here) . Another explanation is that good ideas are getting harder to find, and hence it requires an increasingly large technological input to get additional output.

The trillion dollar question is whether AI will break the 2% trend or not. Will AI be just another technology that allows us to sustain 2% growth for another couple of decades? Or will the “AI moment”  be for us like post-WWII Japan? That is, should we model it as if we are meeting a new “AI frontier economy” which is vastly more productive, and this interaction will enable rapid growth, with GDP at least doubling every decade as was the case for Japan. 

To put things in perspective, Acemuglu predicts AI driven GDP growth to be about 0.1% per year while Goldman Sachs predicts about 1.5% over a year. GDP doubling over a decade would correspond to roughly 7% growth per year, or AI contributing around 5% additional growth - more than triple the Goldman Sachs estimate, and 50 times higher than Acemuglu’s estimates. The consequences of even a “minor” boost in growth can be massive. A 1.2% increase in GDP growth would be sufficient to put the U.S. economy on fiscally sustainable footing, with no need for increased taxes or decreased spending, while a 2% increase in GDP growth would be unprecedented for the U.S. 

AI can contribute to GDP growth by either enabling replacement of labor with capital, or increasing total factor productivity. Specifically, some versions of endogenous growth theory stipulate that productivity grows with the production of ideas, and this production is in turn monotonically (though not linearly) related to the number of researchers/inventors. 

If AI contributes via automating a specific industry, then the maximum benefit to the GDP is bounded by the share of this industry. Specifically, if an industry amounts for x fraction of the economy then (according to the model of B. Jones, see below)  automating it fully can boost GDP by at most 1/(1-x). E.g., full automation of the software industry can increase the GDP by 1/0.98~ 2%. Depending on how you measure it, cognitive labor arguably amounts to at least 30% of GDP (e.g. half of labor share of GDP) and so full automation of it could increase it by 1/0.7 ~ 42%. If the latter happens over a decade that would already correspond to 3.5% annual growth.  

However, if AI also improves productivity of other industries (e.g. by discovering new ideas) then the contribution can grow even beyond those that are not directly automated. To be clear, to the extent AI contributes to research and development, I expect this would be by accelerating science and making scientists, researchers,  and inventors more productive. This means that in the coming years, funding human scientists will offer an even higher return on investment than it has in the past. 

Below I offer some vague intuitions and unfounded extrapolations to try to get at how much and how fast we could expect AI to contribute to growth.

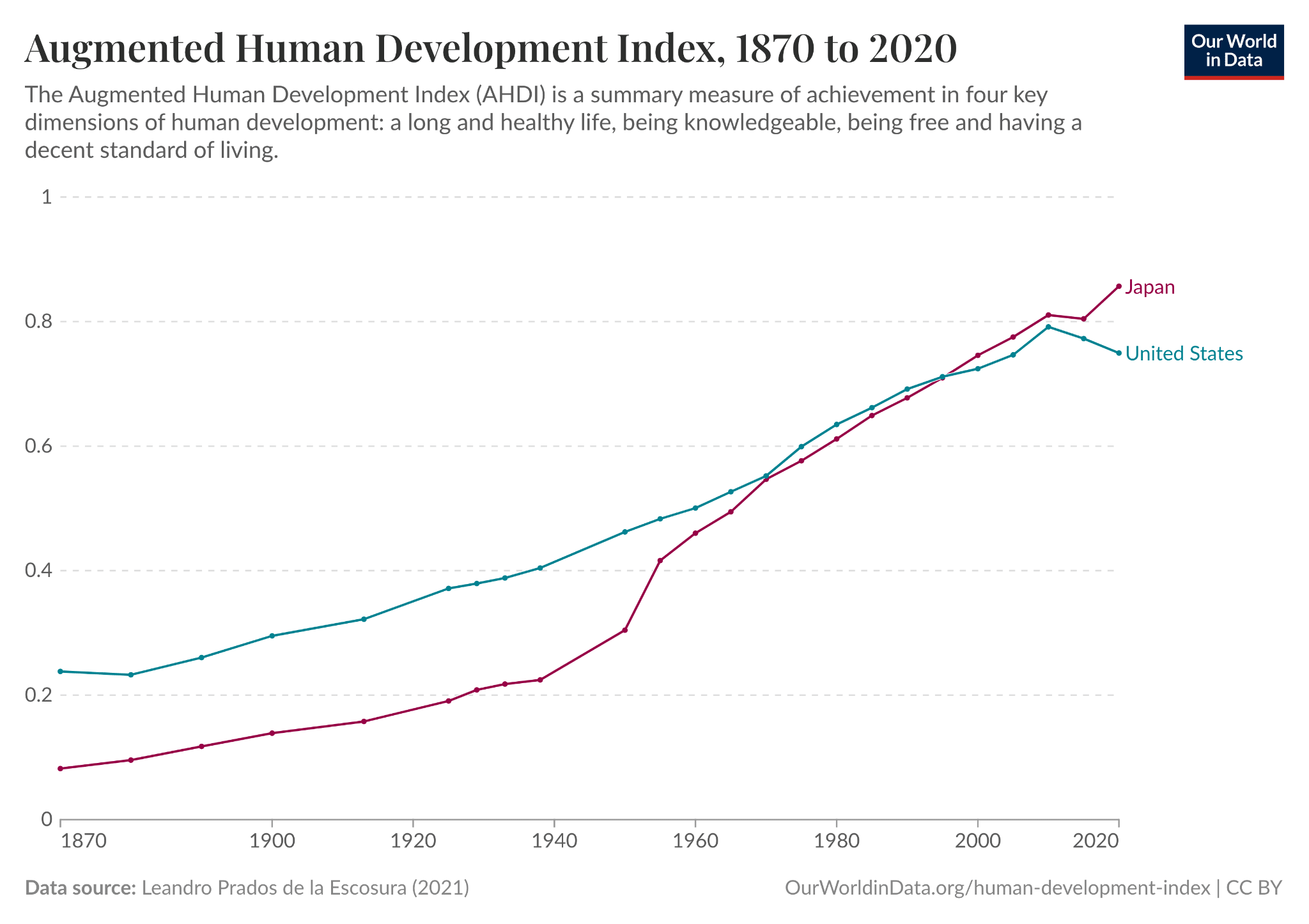
Note that there are critiques of GDP as a measure of progress, and various alternative measures have been proposed. However, many of these are also at least loosely correlated with GDP, with a spike in one corresponding to a spike in the other. E.g., see this chart of the augmented human development index of the U.S. and Japan.

While I am sure many of AI’s impacts will not be captured by the GDP, I believe that if it will be truly as transformative as the industrial revolution, this will show up in the GDP as well.

Intuition from METR tasks

Let us make the (very rough and not really justified) assumption that in a certain industry or job, the tasks are “heavy tailed” where the fraction of tasks that take a person at least T time to complete shrinks proportionally to 1/T.  In this case, the time horizon is proportional to the fraction of tasks that have not been automated. This means that the “doubling time” is the same as the “halving time” of the fraction of tasks that have not been automated yet.

Another way to think about it is by thinking of the “ELO analogy” - assume the distribution of “ELO ratings” of tasks is such that the fraction of tasks with an ELO rating more than E is roughly exp(-E).  (For chess players the distribution of ELO scores is roughly normal, which would be ~ exp(-E²).) 

If we assume a “halving time” of 6 months, it would take about 2 years from the point of time that AI’s automates half of the tasks in some industry, to the point in time that they automate 31/32 ~ 97% of the tasks in it.

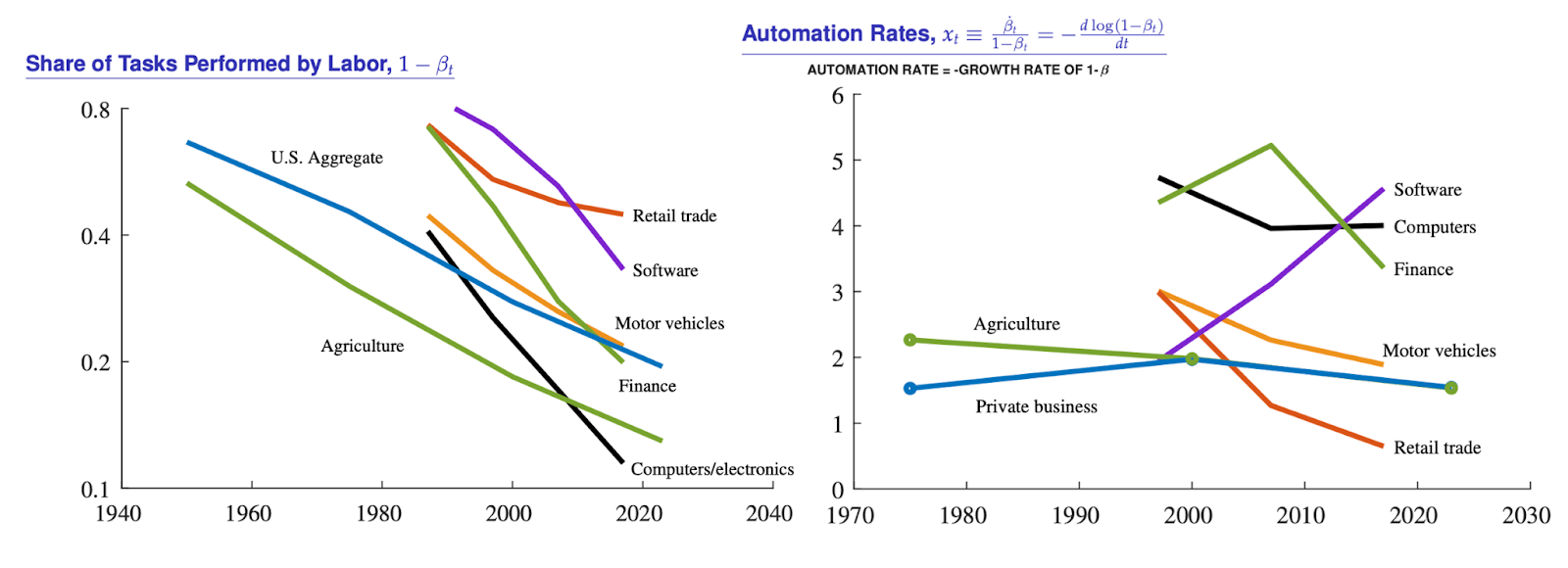
This assumption is extremely aggressive in the sense that it is focused on capabilities and ignores diffusion. It is possible that AI could theoretically automate a large fraction of tasks but for many reasons it would not automate them in practice. (Though it is also possible that diffusion will progress unevenly, with sudden unlocking of latent capabilities.)  It is also important to note that this intuition runs counter to broad trends in automation over the last 80 years which have historically been linear - with the share of automated tasks growing slowly and steadily, with a single-digit percent rate of automation that is often declining over time. See the following charts from C. Jones and Tonetti (2025), via ChatGPT:

Hence if AI will cause an exponential decay of the share of tasks performed by labor, it would be a break with previous trends in automation and very different from what we have seen in the past.

AI as increasing population

One way to view AI is as injecting to the economy each year t a number N(t) of new “workers” that have a certain quality Q(t) - quality could correspond to the fraction of economically useful tasks these workers can do, so can correspond to both “years of schooling” and the generality of their ability. We can define Q(t) as one over the fraction of tasks that have not yet been automated in the corresponding industry.

Algorithmic advances in AI and the overall compute budget will determine the mixture of workers and quality. As a point of comparison, the U.S. population has been growing at about 2m per year due to natural growth and immigration, and the U.S. labor force is about 160m people.

At a rough level, if capital and productivity is fixed, and we assume a Cobb-Douglas production function with GDP being proportional to KᵃL¹⁻ᵃ with a=0.4 then increasing the labor force by a factor of C will increase the GDP by a factor of C⁰ᐧ⁶. If AI creates 10m new virtual employees, that would increase the GDP by a factor of (170/160)⁰ᐧ⁶  which is about 4 percent. 

If it is 50m new employees this would be about 18%, and if AI doubles the workforce then the growth would be ~50%. Of course, the number of AI “virtual workers” could potentially be orders of magnitude more, at which point these calculations are likely not to make much sense. (There is a book called “One Billion Americans” but I think even its author did not ponder what would happen if there were one trillion Americans...) 

It is hard to give predictions on either N(t) or Q(t), but it seems reasonable to expect that both will grow exponentially. At the extreme, if we fix the quality Q then we could expect N(t) to increase 10x per year (as costs for a fixed model quality have decreased.) But perhaps a starting point assumption would be that the product of both will grow at the 4x/year METR rate, with both Q and N doubling every year.  (Note that N(t) is the number of new workers, and so is equal to TN(t)-TN(t-1) where TN(t) is the total number of AI workers at year t, however since the derivative of an exponential is exponential then it does not matter, especially if the base of this exponential is 2.) 

Such growth is sufficient to ensure that once AI starts providing a non-trivial number of new workers (e.g., 100K workers in the U.S.) then within a decade, AI will be the dominant source of labor in the U.S.

Substitution and automation effects

A simplified version of the model of B. Jones (2025) is that the impact of AI on productivity is determined by the harmonic mean of the automatable and non automatable tasks. 

Imagine that a ρ fraction of R&D tasks cannot be automated, and 1-ρ fraction of tasks can be automated and be carried out at far lower cost than humans. For simplicity, let’s assume that the human productivity in non-automated tasks is 1, and the AI productivity in automated tasks is λ>>1.

Then the improvement in productivity due to automation can be modeled as the Harmonic average of 1 and λ with weights ρ and 1-ρ respectively, that is:

(ρ/1 + (1−ρ)/λ)⁻¹

Note that unlike the arithmetic or geometric means, even if λ is infinite, the maximum that this can reach is 1/ρ. This makes sense if we think of tasks as non-substitutable and so the maximum productivity gain we can get is if we automated tasks that take humans 90% of the time, so that now one worker can do 10x time the work per time unit.

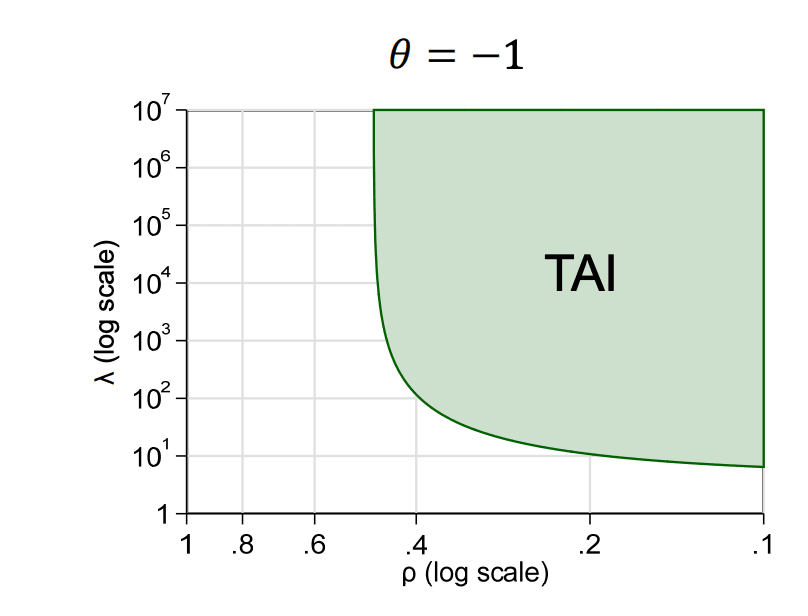
Jones shows that in such a model, in order to get significant productivity gains, both ρ must shrink and λ must grow. If one of them stays “stuck” then so will productivity. Jones has the following graph of the regimes where we can get “transformative AI” in the sense of 10x productivity growth, which would be similar to the scale of the productivity increase via the industrial revolution. (If I am following the math correctly, the condition under Jones’ assumptions for this graph is that 9/[(2−ρ)/√ λ + 2ρ]²  ≥ 10.)

Figure 5 in Jones: Regime of λ,ρ that leads to transformative AI in harmonic mean case.

One way to think about this graph is what happens if we assume that, via the mechanisms discussed above, every year we make progress in both ρ (fraction of tasks not yet automated) and λ (productivity factor of AI in doing these tasks). 

As discussed above, it is a “leap of faith” but arguably not completely crazy to assume that at some point (maybe once we reach a threshold such as AIs doing 8 hours of work) ρ will shrink by a factor of 4x per year, while λ will increase by a factor of 10x per year. At this rate, within a year, we would move from the lefthand corner of this graph (1,1) to the point λ =10 , ρ=¼ which is almost at the TAI boundary.  (Note that Jones assumes that half of the tasks have already been automated, so it might take us a while to get to the lefthand corner of the graph. Also, accounting for the “ideas getting harder to find” effect could decrease the shrinking rate, see section 4.4 in the paper.)

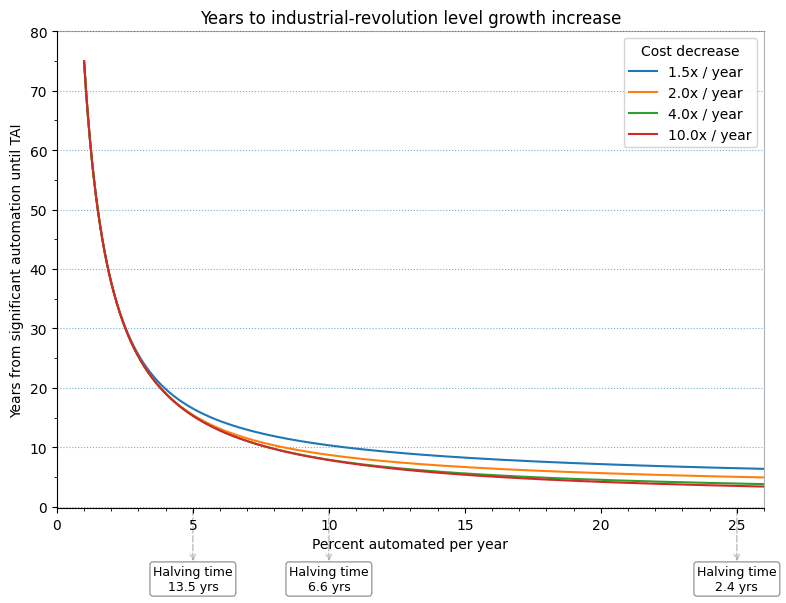
The assumption on ρ shrinking by a 4x factor is very aggressive and arguably unrealistic. Perhaps a much smaller factor such as 1.1 is more reasonable, which would correspond to automating a 1/1.1 ~ 9% of remaining tasks each year (as opposed to 75% in the case of 4x shrinkage of ρ). Here is a plot of how many years from the (1,1) corner it will take for transformative AI as a function of the fraction of tasks automated per year, for various values of cost decrease (growth in λ).

We see that as long as the rate is significant, we can get to transformative growth within one to two decades. Note also that this is less sensitive to decrease in costs (growth in λ), which could bode well for automating manual tasks. 

The bottom line is that the question on whether AI can lead to unprecedented growth amounts to whether its exponential growth in capabilities will lead to the fraction of unautomated tasks itself decreasing at exponential rates.

Acknowledgements: Thanks to Bharat Chandar, Jason Furman, Benjamin Jones and Chad Jones for comments and discussions on this post.