Superhuman math AI will plausibly arrive significantly before broad automation
I think it's plausible that for several years in the late 2020s/early 2030s, we will have AI that is vastly superhuman at formal domains including math, but still underperforms humans at most white-collar jobs (and so world GDP growth remains below 10%/year, say – still enough room for AI to be extraordinarily productive compared to today).
Of course, if there were to be an intelligence explosion on that timescale, then superhuman math AI would be unsurprising. My main point is that superhuman math AI still seems plausible even disregarding feedback loops from automation of AI R&D. On the flip side, a major catastrophe and/or coordinated slowdown could prevent both superhuman math AI and broad automation. Since both of these possibilities are widely discussed elsewhere, I will disregard both AI R&D feedback loops and catastrophe for the purposes of this forecast. (I think this is a very salient possibility on the relevant timescale, but won't justify that here.)
My basic reasons for thinking vastly superhuman math AI is a serious possibility in the next 4–8 years (even absent AI R&D feedback loops and/or catastrophe):
- Performance in formal domains is verifiable: math problems can be designed to have a unique correct answer, and formal proofs are either valid or invalid. Historically, in domains with cheap, automated supervision signals, only a relatively small amount of research effort has been required to produce superhuman AI (e.g., in board games and video games). There are often other bottlenecks than supervision, most notably exploration and curricula, but these tend to be more surmountable.
- Recent historical progress in math has been extraordinarily fast: in the last 4 years, AI has gone from struggling with grade school math to achieving an IMO gold medal, with progress at times exceeding almost all forecasters' reasonable expectations. Indeed, much of this progress seems to have been driven by the ability to automatically supervise math, with reasoning models being trained using RL on a substantial amount of math data.
Superhuman math AI looks within reach without enormous expense: reaching superhuman ability in a domain requires verifying solutions beyond a human's ability to produce them, and so a static dataset produced by humans isn't enough. (In fact, a temporary slowdown in math progress in the near future seems possible because of this, although I wouldn't bet on it.) But the following two ingredients (plus sufficient scale) seem sufficient for superhuman math AI, and within reach:
- Automatic problem generation: the ability to generate a diverse enough set of problems such that both (a) most realistic math of interest to humans is within distribution and (b) problem difficulty is granular enough to provide a good curriculum. Current LLMs with careful prompting/fine-tuning may be enough for this.
- Reliable informal-to-formal translation: solution verifiers need to be robust enough to avoid too much reward hacking, which probably requires natural language problems and solutions to be formalized to some degree (a variety of arrangements seem possible here, but it's hard to see how something purely informal can provide sufficiently scalable supervision, and it's hard to see how something purely formal can capture mathematicians' intuitions about what problems are interesting). This is basically a coding problem, and doesn't seem too far beyond the capabilities of current LLMs. Present-day formalization efforts by humans are challenging, but in large part because of their laboriousness, which AI is excellent at dealing with.
Note I'm not claiming that there will be discontinuous progress once these ingredients "click into place". Instead, I expect math progress to continue on a fast but relatively continuous trajectory (perhaps with local breakthroughs/temporary slowdowns on the order of a year or two). The above two ingredients don't seem especially responsible for current math capabilities, but could become increasingly relevant as we move towards and into the superhuman regime.
By contrast, some reasons to be skeptical that AI will be automating more than a few percent of the economy by 2033 (still absent AI R&D feedback loops and/or catastrophe):
- Progress in domains in which performance is hard to verify has been slower: by comparison with the dramatic progress in math, the ability of an AI to manage a small business enterprise is relatively unimpressive. In domains with a mixture of formal and informal problem specifications, such as coding, progress has been similarly fast to math, or perhaps a little slower (as measured by horizon length), but my qualitative impression is that has been driven by progress on easy-to-verify tasks, with some transfer to hard-to-verify tasks. I expect to continue to see domains lag behind based on the extent to which performance is easy to verify.
- Possible need for expensive long-horizon data: in domains with fuzzy, informal problem specifications, or requiring expensive or long-horizon feedback from the real world, we will continue to see improvements, since there will be transfer both from pretraining scaling and from more RL on verifiable tasks. But for tasks where this progress is slow despite the task being economically important, it will eventually be worth it to collect expensive long-horizon feedback. However, it might take several years to scale up the necessary infrastructure for this, unlike some clear routes to superhuman math AI, for which all the necessary infrastructure is essentially already in place. This makes a 2–5+ year lag seem quite plausible.
- Naive revenue extrapolation: one way to get a handle on the potential timescale until broad automation is to extrapolate AI company revenues, which are on the order of tens of billions of dollars per year today, around 0.01% of world GDP. Even using OpenAI's own projections (despite their incentives to make overestimates), which forecast that revenue will grow by a factor of 10 over the next 4 years, and extrapolating them an additional 4 years into the future, gives an estimate of around 1% of world GDP by 2033. AI companies won't capture all the economic value they create, but on the other hand this is a very bullish forecast by ordinary standards.
What would a world with vastly superhuman math AI, but relatively little broad automation, look like? Some possibilities:
- Radical effect on formal sciences: by "vastly superhuman math AI", I mean something like: you can give an AI a math problem, and it will respond within e.g. a couple of hours with a formal proof or disproof, as long as a human mathematician could have found an informal version of the proof in say 10 years. (Even though I just argued for the plausibility of this, it seems completely wild to comprehend, spelled out explicitly.) I think this would completely upend the formal sciences (math, theoretical computer science and theoretical physics) to say the least. Progress on open problems would be widespread but highly variable, since their difficulty likely ranges from "just out of reach to current mathematicians" to "impossible".
- Noticeable speed-up of applied sciences: it's not clear that such a dramatic speed-up in the formal sciences would have that dramatic consequences for the rest of the world, given how abstract much of it is. Cryptography, formal verification and programming languages might be the most consequential areas, followed by areas like experimental physics and computational chemistry. However, in most of the experimental sciences, formal results are not the main bottleneck, so speed-ups would be more dependent on progress on coding, fuzzier tasks, robotics, and so on. Math-heavy theoretical AI alignment research would be significantly sped up, but may still face philosophical hurdles.
- Broader economy: it's worth emphasizing that even if world GDP growth remains below 10%/year, that still leaves plenty of room for AI to feel "crazy", labor markets to be dramatically affected by ordinary standards, political discussion to be dominated by AI, etc. Note also that this period may be fairly short-lived (e.g., a few years).
Such a scenario is probably poor as an all-things-considered conditional forecast, since I've deliberately focused on a very specific technological change, but it hopefully adds some useful color to my prediction.
Finally, some thoughts on whether pursuing superhuman math AI specifically is a beneficial research direction:
- Possibility for transfer: there is a significant possibility that math reasoning ability transfers to other capabilities; indeed, we may already be seeing this in today's reasoning models (though I haven't looked at ablation results). That being said, moving into the superhuman regime and digging into specialist areas, math ability will increasingly be driven by carefully-tuned specialist intuitions, especially if pursuing something like the informal-to-formal approach laid out above. Moreover, specialized math ability seems to have limited transfer in humans, and transfer in ML is generally considerably worse than in humans. Overall, this doesn't seem like a dominant consideration.
- Research pay-offs: a different kind of "transfer" is that pursuit of superhuman math AI would likely lead to general ML research discoveries, clout, PR etc., making it easier to develop other AI capabilities. I think this is an important consideration, and probably the main reason that AI companies have prioritized math capabilities so far, together with tractability. However, pursuing superhuman math AI doesn't seem that different from other capabilities research in this regard, so the question of how good it is in this respect is mostly screened off by how good you think it is to work on capabilities in general (which could itself depend on the context/company).
- Differential progress: the kinds of scientific progress that superhuman math AI would enable look more defense-oriented than average (e.g., formal verification), and I think the possibility of speeding up theoretical AI alignment research is significant (I work in this area and math AI is already helping).
- Replaceability: there are strong incentives for AI companies and for individual researchers to pursue superhuman math AI anyway (e.g., the research pay-offs discussed above), which reduces the size (in either direction) of the marginal impact of an individual choosing to work in the area.
Overall, pursuing superhuman math AI seems mildly preferable to working on other capabilities, but not that dissimilar in its effects. It wouldn't be my first choice for most people with the relevant skillset, unless they were committed to working on capabilities anyway.
Couldn't agree more!
One of the saddest ways we would die is if we fail to actually deploy enough theory/math people to work on prompting AIs to solve alignment in the next two-three years, even if it would be totally possible to solve alignment this way.
P.S. Please get into contact if you are interested in this.
You can give an AI a math problem, and it will respond within e.g. a couple of hours with a formal proof or disproof, as long as a human mathematician could have found an informal version of the proof in say 10 years.
Suppose you had a machine like this right now, and it cost $1 per query. How would you use it to improve things?
Reliable informal-to-formal translation: solution verifiers need to be robust enough to avoid too much reward hacking, which probably requires natural language problems and solutions to be formalized to some degree (a variety of arrangements seem possible here, but it's hard to see how something purely informal can provide sufficiently scalable supervision, and it's hard to see how something purely formal can capture mathematicians' intuitions about what problems are interesting).
Do you think OpenAI and GDM's recent results on IMO are driven by formalization in training (e.g. the AI formalizes and checks the proof) or some other verification strategy? I'd pretty strongly guess some other verification strategy that involves getting AIs to be able to (more) robustly check informal proofs. (Though maybe this verification ability was partially trained using formalization? I currently suspect not.) This also has the advantage of allowing for (massive amounts of) runtime search that operates purely using informal proofs.
I think an important alternative to informal-to-formal translation is instead just getting very robust AI verification of informal proofs that scales sufficiently with capabilities. This is mostly how humans have gotten increasingly good at proving things in mathematics and I don't see a strong reason to think this is infeasible.
If superhuman math is most easily achieved by getting robust verification and this robust verification strategy generalizes to other non-formal but relatively easy to check domains (e.g. various software engineering tasks), then we'll also see high levels of capability in these other domains, including domains which are more relevant to AI R&D and the economy.
Agree about recent results not being driven by formalization, but I'd also guess having ground truth (e.g. numeric answers or reference solutions) remains pretty important, which doesn't scale to the superhuman regime.
Agree that evidence from humans means reaching superhuman capability through purely informal proof is possible in principle. But ML is less robust than humans by default, and AI is already more proficient with formal proof systems than most mathematicians. So informal-to-formal seems like a natural consequence of increased tool use. Not confident in this of course.
I expect easy-to-check software engineering tasks (and tasks that are conceptually similar to easy-to-check tasks) to be pretty close to math, and harder-to-check/fuzzier tasks to lag. Most tasks in the broad economy seem like they fall in the latter category. The economy will likely adapt to make lots of tasks better suited to AI, but that process may be slower than the capability lag anyway. AI R&D might be a different story, but I will leave that to another discussion.
However, in most of the experimental sciences, formal results are not the main bottleneck, so speed-ups would be more dependent on progress on coding, fuzzier tasks, robotics, and so on
One difficulty with predicting the impact of "solving math" on the world is the Jevons effect (or a kind of generalization of it). If posing a problem formally becomes equivalent to solving it, it would have effects beyond just speeding up existing fully formal endeavors. It might potentially create qualitatively new industries/approaches relying on cranking out such solutions by the dozens.
E. g., perhaps there are some industries which we already can fully formalize, but which still work in the applied-science regime, because building the thing and testing it empirically is cheaper than hiring a mathematician and waiting ten years. But once math is solved, you'd be able to effectively go through dozens of prototypes per day for, say, $1000, while previously, each one would've taken six months and $50,000.
Are there such industries? What are they? I don't know, but I think there's a decent possibility that merely solving formal math would immediately make things go crazy.
This is what came to mind for me:
"But once [protein structure prediction] is solved [-ish], you'd be able to effectively go through dozens of [de novo proteins] per day for, say, $1000 [each], while previously, each one would've taken six months and $50,000."
By contrast, some reasons to be skeptical that AI will be automating more than a few percent of the economy by 2033 (still absent AI R&D feedback loops and/or catastrophe):
I currently expect substantial AI R&D acceleration from AIs which are capable of cheap and fast superhuman performance at arbitrary easy-and-cheap-to-check domains (especially if these AIs are very superhuman). Correspondingly I think "absent AI R&D feedback loops" might be doing a lot of the work here. Minimally, I think full automation of research engineering would yield a large acceleration (e.g. 3x faster AI progress), though this requires high performance on (some) non-formal domains. I think if AIs were (very) superhuman at easy (and cheap) to check stuff, you'd probably be able to use them to do a lot of coding tasks, some small scale research tasks that might transfer well enough, and there would be a decent chance of enough transfer to extend substantially beyond this.
I think I still agree with the bottom line "it's plausible that for several years in the late 2020s/early 2030s, we will have AI that is vastly superhuman at formal domains including math, but still underperforms humans at most white-collar jobs". And I agree more strongly if you change "underperforms humans at most white-collar jobs" to "can't yet fully automate AI R&D".
I think one can make a stronger claim that the Curry-Howard isomorphism mean a superhuman (constructive?) mathematician would near-definitionally be a superhuman (functional?) programmer as well.
Performance in formal domains is verifiable
This is a VERY important factor, possibly the only one that really matters. Along with "no harm, just retry or defer failed/unverifiable attempts", which applies to lots of math, and very few real-world uses.
Noticeable speed-up of applied sciences: it's not clear that such a dramatic speed-up in the formal sciences would have that dramatic consequences for the rest of the world, given how abstract much of it is. Cryptography, formal verification and programming languages might be the most consequential areas, followed by areas like experimental physics and computational chemistry. However, in most of the experimental sciences, formal results are not the main bottleneck, so speed-ups would be more dependent on progress on coding, fuzzier tasks, robotics, and so on. Math-heavy theoretical AI alignment research would be significantly sped up, but may still face philosophical hurdles.
Its not clear that the primary bottleneck to formal sciences are proofs either. I get the impression from some mathematicians that the big bottlenecks are in new ideas, so in the "what do you want to prove?" question, rather than the "can you prove x?" question. That seems much less formally verifiable.
This reminds me of L Rudolf L's A history of the future scenario-forecasting how math might get solved first, published all the way back in February (which now feels like an eternity ago):
A compressed version of what happened to programming in 2023-26 happens in maths in 2025-2026. The biggest news story is that GDM solves a Millennium Prize problem in an almost-entirely-AI way, with a huge amount of compute for searching through proof trees, some clever uses of foundation models for heuristics, and a few very domain-specific tricks specific to that area of maths. However, this has little immediate impact beyond maths PhDs having even more existential crises than usual.
The more general thing happening is that COT RL and good scaffolding actually is a big maths breakthrough, especially as there is no data quality bottleneck here because there’s an easy ground truth to evaluate against—you can just check the proof. AIs trivially win gold in the International Mathematical Olympiad. More general AI systems (including increasingly just the basic versions of Claude 4 or o5) generally have a somewhat-spotty version of excellent-STEM-postgrad-level performance at grinding through self-contained maths, physics, or engineering problems. Some undergrad/postgrad students who pay for the expensive models from OpenAI report having had o3 or o5 entirely or almost entirely do sensible (but basic) “research” projects for them in 2025.
Mostly by 2026 and almost entirely by 2027, the mathematical or theoretical part of almost any science project is now something you hand over to the AI, even in specialised or niche fields. ...
(there's more, but I don't want to quote everything. Also IMO gold already happened, so nice one Rudolf)
this is quite interesting, and I share the intuition that superhuman math is likely. I think go and other board games are indeed a good analogy, and we could see takeoff from self-play
even if super it relies on formalization and doesn't directly generalize to other fields, I still wonder if superhuman math wouldn't have bigger real consequences than Ryan thinks. Here is some speculation:
- AI research
- we still don't have a complete mathematical theory for why deep learning works. A superhuman AI in math could help human experts develop a "theory of deep learning," which could allow us to move from brute-force experimentation to principled design of deep networks
- Our networks are still absurdly inefficient compared to the brain, prob because spike-timing information is more efficient than info coding in weights only. spiking neural networks are too hard to design and train, but better theoretical results would maybe improve the situation
- More efficient optimizers to train current networks via computer science theoretical results
- Fusion energy
- Designing stable plasma confinement in a fusion reactor requires solving intractable differential equations. Maybe maths results could make them more tractable
Current LLMs can actually help us speculate better on what would be possible, I'd be curious to see more people posting here on ways superhuman maths could be impactful.
I am willing to bet money on there existing superhuman AI mathematicians by the end of 2026 with atleast ... idk 50% probability. I want the bet to give me asymmetric upside if I'm right though.
Strong agree. Not to appeal to much to authority, but Terence Tao has already to move his main focus to worked on AI powered proof solving software. I don't have a formal survey, but talking to mathematicians I know, there's a feeling this is coming soon.
Okay, looking back over, "main focus", is a bit of an over statement, but it's definitely one of his big fields of interest at the moment. According to him frontier models are currently ~5x ish multiple time harder to get productive in helping you solve complex novel math than a grad student. (dependent on the grad student & the problem). Note: my original statement was based on recollection of conversations I've had with a mathematician I trust at CalTech who works in the same circles, take that as you will
Task duration as a Bradley–Terry score: an alternative to the constant hazard rate model
@Toby_Ord writes about the constant hazard rate model for task duration: a long task can be thought of as a sequence of many short subtasks of fixed difficulty, each of which must be completed to complete the overall task. This explains the approximately sigmoidal relationship between log(task horizon length) and the probability that a given model successfully completes the overall task.
I think this is a useful conceptual framing that explains the data reasonably well. But there is at least one alternative that explains the data about as well, which is to think of the task duration as being similar to a Bradley–Terry score, i.e., an exponential of an Elo rating.
The underlying intuition is that, in addition to having a larger number of subtasks, a longer task also has a higher probability of having a particularly hard subtask. We can crudely approximate the difficulty of a long task by the difficulty of its hardest subtask.
Concretely, consider any fixed random number distribution (e.g. uniform over [0,1]), representing the difficulty of a subtask. Assign to each task a positive integer , and to each model a positive integer . To decide whether successfully completes , we draw random numbers from our distribution for the task, and random numbers for the model. We then say that the task is completed if the model's largest number exceeds the task's largest number. Thus the probability of completion is
where is the sigmoid function. This explains the sigmoidal relationship observed in Figure 5 of METR's paper.
Toby's model produces an exponential relationship, which is similar but slightly different to a sigmoid on a log scale. He argues that his relationship is preferred because it has only one free parameter instead of two. However, our model allows us to determine what one of the parameters of the sigmoidal relationship should be, by assuming that is proportional to the task duration. This predicts that the (negated) coefficient of the sigmoidal relationship should be around 1, assuming the natural log is applied to the task duration. At the very least, for a fixed task distribution, the coefficients should be similar for different models.
We can test this prediction by running the code used to produce Figure 5 to get the coefficient and intercept of the logistic regression.[1] Since the code applies a base-2 logarithm to the task duration, we can negate and divide the coefficient by the natural log of 2 to get the appropriately-scaled coefficient for our purposes:
| Agent | Coefficient | Intercept | Coefficient / (-log(2)) |
| Claude 3 Opus | -0.55 | 1.48 | 0.80 |
| Claude 3.5 Sonnet (New) | -0.52 | 2.55 | 0.76 |
| Claude 3.5 Sonnet (Old) | -0.55 | 2.31 | 0.80 |
| Claude 3.7 Sonnet | -0.70 | 4.13 | 1.01 |
| GPT-2 | -0.49 | -2.29 | 0.71 |
| GPT-4 0125 | -0.64 | 1.55 | 0.92 |
| GPT-4 0314 | -0.56 | 1.36 | 0.81 |
| GPT-4 1106 | -0.54 | 1.68 | 0.78 |
| GPT-4 Turbo | -0.66 | 1.79 | 0.95 |
| GPT-4o | -0.57 | 1.82 | 0.82 |
| davinci-002 (GPT-3) | -0.65 | -1.79 | 0.94 |
| gpt-3.5-turbo-instruct | -0.78 | -0.56 | 1.13 |
| human | -0.39 | 2.55 | 0.56 |
| o1 | -0.51 | 2.70 | 0.74 |
| o1-preview | -0.61 | 2.73 | 0.88 |
Even as the intercept varies considerably, the coefficient (divided by -log(2)) is relatively consistent and generally close to 1. It tends to be a little lower than 1, which is what you would expect if task duration measurements were noisy approximations to the value of , since this would flatten the slope of the sigmoid.
In reality, neither the constant hazard rate model nor the Bradley–Terry model is perfect. The constant hazard rate model fails to account for the fact that models can recover from small errors, while the Bradley–Terry model fails to account for the fact that models can fail because of subtasks that are easier than the hardest subtask.
The Bradley–Terry model has the advantage that it specifically explains why we might expect the relationship to be sigmoidal rather than approximately sigmoidal, and shows why we may need an extra free parameter to account for noisy measurements of task duration. It also more analogous to the scaling behavior of reinforcement learning observed previously in other settings, such as in Hex and Dota 2, where TrueSkill/Elo rating scales as a power law in compute. See in particular the toy model described in the Hex paper, which inspired the description I gave here:
The way in which performance scales with compute is that an agent with twice as much compute as its opponent can win roughly 2/3 of the time. This behaviour is strikingly similar to that of a toy model where each player chooses as many random numbers as they have compute, and the player with the highest number wins.
The ideal model would probably combine both aspects – that longer tasks have both more subtasks and harder subtasks. But this would have the downside of introducing more free parameters, and the data is likely to be too noisy to fit these in the near future. Overall, sticking to fitting two-parameter sigmoids is probably the way to go for now.
- ^
After installing the eval-analysis-public repo, I obtained these numbers by running the following command:
mkdir data/wrangled/logistic_fits; python -m src.wrangle.logistic --fig-name headline --runs-file data/external/all_runs.jsonl --output-logistic-fits-file data/wrangled/logistic_fits/headline.csv --release-dates data/external/release_dates.yaml --bootstrap-file data/wrangled/bootstrap/headline.csv. Thanks to Nate Rush for help with this.
Thanks for this Jacob — excellent analysis.
I'm a huge fan of Bradley-Terry models. I'm quite sure they are the natural way of representing noisy contests like chess ability and that Elo is an inferior way. They key thing with Bradley-Terry is that each competitor has a raw ability score (e.g. A and B) and that then when they have a contest the odds of A beating B is just A:B. I think of it as each player puts a number of tickets of their colour into a hat and then one is drawn at random determining the winner. This is an even simpler interpretation than the one from the Hex paper and makes the 2/3 result even more intuitive.
Elo then takes the log base 10 and multiplies by 400 and then adds 1200 or so to make the numbers usually positive, injecting three (!) arbitrary constants into the mix in order to give an additive scale that matched the pre-Elo chess rating scale — but the natural interpretation of these contests is a multiplicative scale (the ratio of the numbers is the odds ratio of winning) so it should have been left alone. Linear progress in Elo is really exponential progress in the raw quantity.
I like your idea of assuming random difficulties for the different tasks (from some distribution that could be tweaked), as clearly that is part of the real underlying phenomenon. However, it is weird that you compare the highest number the agent draws from the hat to the highest number the task draws. More natural would be to have to take on the tasks one by one in a gauntlet of challenges of varying difficulty. e.g. that the probability of success is instead of my where is a random variable drawn from some natural distribution over [0,1] that is modified by the agent's skill and represents the probability of succeeding at that subtask. There should be limiting cases where all are equal (my case) and where it is driven by the hardest one. But I'm not sure what distribution this creates.
That said, I like where you are going with this and how you eliminate one of the parameters.
I definitely see my constant hazard rate model as a first order approximation to what is going on, and not the full story. I'm surprised it works as well as it does because the underlying phenomenon has more structure than this. So I see it just as something of a null hypothesis for other approaches to beat, and do expect it to eventually be beaten.
In figure 5 the X axis is log time horizon and not time horizon - does this fit with your model?
Yes, unless I messed up, METR's code runs a logistic regression of (task duration) against success probability, so my model predicts a raw fitted coefficient (the second column in the table) close to -ln(2) ≈ -0.69.
Oh right sorry I missed the derivation that among samples, the maximum is equally likely to be any of them and so the probability that the largest number from the model the largest of them is
This model then predicts that models "ELO ratings" - would grow linearly over time, which (based on this chart GPT5 gave me) I think corresponds roughly with the progress in chess from 2007 onwards
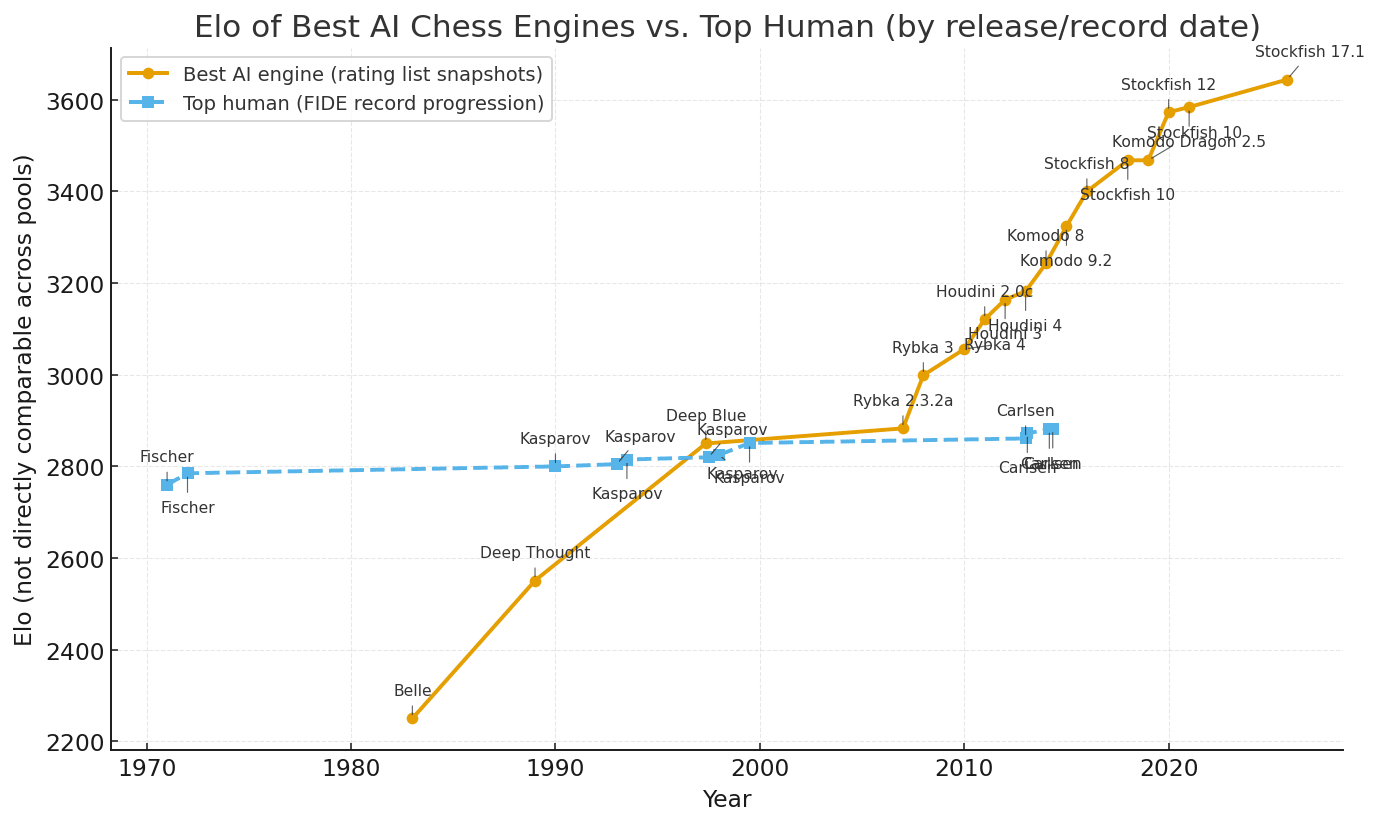
It also makes the quantitative prediction that a doubling in compute (or compute efficiency) leads to a 2/3 win probability, or around 120 Elo points. (Credit to the Hex paper for this observation.) Under 18-month doublings (per one version of Moore's law), this would be around 800 Elo points per decade, which looks like a bit of an overestimate but similar to the fastest observed rate of progress.
Against superexponential fits to current time horizon measurements
I think is unreasonable to put non-trivial weight (e.g. > 5%) on a superexponential fit to METR's 50% time horizon measurements, or similar recently-collected measurements.
To be precise about what I am claiming and what I am not claiming:
- I am not claiming that these measurements will never exhibit a superexponential trend. In fact, I think a superexponential trend is fairly likely eventually, due to feedback loops from AI speeding up AI R&D. I am claiming that current measurements provide almost no information about such an eventuality, and naively applying a superexponential fit gives a poor forecast.
- I am not claiming that is very unlikely for the trend to be faster in the near future than in the near past. I think a good forecast would use an exponential fit, but with wide error bars on the slope of the fit. After all, there are very few datapoints, they are not independent of each other, and there is measurement noise. I am claiming that extrapolating the rate at which the trend is getting faster is unreasonable.
- My understanding is that AI 2027's forecast is heavily driven by putting substantial weight on such a superexponential fit, in which case my claim may call into question the reliability of this forecast. However, I have not dug into AI 2027's forecast, and am happy to be corrected on this point. My primary concern is with the specific claim I am making rather than how it relates to any particular aggregated forecast.
Note that my argument has significant overlap with this critique of AI 2027, but is focused on what I think is a key crux rather than being a general critique. There has also been some more recent discussion of superexponential fits since the GPT-5 release here, although my points are based on METR's original data. I make no claims of originality and apologize if I missed similar points being made elsewhere.
The argument
METR's data (see Figure 1) exhibits a steeper exponential trend over the last year or so (which I'll call the "1-year trend") than over the last 5 years or so (which I'll call the "5-year trend"). A superexponential fit would extrapolate this to an increasingly steep trend over time. Here is my why I think such an extrapolation is unwarranted:
- There is a straightforward explanation for the 1-year trend that we should expect to be temporary. The most recent datapoints are all reasoning models trained with RL. This is a new technique that scales with compute, and so we should expect there to be rapid initial improvements as compute is scaled from a low starting point. But this compute growth must eventually slow down to the rate at which older methods are growing in compute, once the total cost becomes comparable. This should lead to a leveling off of the 1-year trend to something closer to the 5-year trend, all else being equal.
- Of course, there could be another new technique that scales with compute, leading to another (potentially overlapping) "bump". But the shape of the current "bump" tells us nothing about the frequency of such advances, so it is an inappropriate basis for such an extrapolation. A better basis for such an extrapolation would be the 5-year trend, which may include past "bumps".
- Superexponential explanations for the 1-year trend are uncompelling. I have seen two arguments for why we might expect the 1-year trend to be the start of a superexponential trend, and they are both uncompelling to me.
- Feedback from AI speeding up AI R&D. I don't think this effect is nearly big enough to have a substantial effect on this graph yet. The trend is most likely being driven by infrastructure scaling and new AI research ideas, neither of which AI seems to be substantially contributing to. Even in areas where AI is contributing more, such as software engineering, METR's uplift study suggests the gains are currently minimal at best.
- AI developing meta-skills. From this post:
"If we take this seriously, we might expect progress in horizon length to be superexponential, as AIs start to figure out the meta-skills that let humans do projects of arbitrary length. That is, we would expect that it requires more new skills to go from a horizon of one second to one day, than it does to go from one year to one hundred thousand years; even though these are similar order-of-magnitude increases, we expect it to be easier to cross the latter gap."
It is a little hard to argue against this, since it is somewhat vague. But I am unconvinced there is such a thing as a "meta-skill that lets humans do projects of arbitrary length". It seems plausible to me that a project that takes ten million human-years is meaningfully harder than 10 projects that each take a million human-years, due to the need to synthesize the 10 highly intricate million-year sub-projects. To me the argument seems very similar to the following, which is not borne out:
"We might expect progress in chess ability to be superexponential, as AIs start to figure out the meta-skills (such as tactical ability) required to fully understand how chess pieces can interact. That is, we would expect it to require more new skills to go from an ELO of 2400 to 2500, than it does to go from an ELO of 3400 to 3500."
At the very least, this argument deserves to be spelled out more carefully if it is to be given much weight.
- Theoretical considerations favor an exponential fit (added in edit). Theoretically, it should take around twice as much compute to train an AI system with twice the horizon length, since feedback is twice as sparse. (This point was made in the Biological anchors report and is spelled out in more depth in this paper.) Hence exponential compute scaling would imply an exponential fit. Algorithmic progress matters too, but that has historically followed an exponential trend of improved compute efficiency. Of course, algorithmic progress can be lumpy, so we shouldn't expect an exponential fit to be perfect.
- Temporary explanations for the 1-year trend are more likely on priors. The time horizon metric has huge variety of contributing factors, from the inputs to AI development to the details of the task distribution. For any such complex metric, the trend is likely to bounce around based on idiosyncratic factors, which can easily be disrupted and are unlikely to have a directional bias. (To get a quick sense of this, you could browse through some of the graphs on AI Impact's Discontinuous growth investigation, or even METR's measurements in other domains for something more directly relevant.) So even if I wasn't able to identify the specific idiosyncratic factor that I think is responsible for the 1-year trend, I would expect there to be one.
- The measurements look more consistent with an exponential fit. I am only eyeballing this, but a straight line fit is reasonably good, and a superexponential fit doesn't jump out as a privileged alternative. Given the complexity penalty of the additional parameters, a superexponential fit seems unjustified based on the data alone. This is not surprising given the small number of datapoints, many of which are based on similar models and are therefore dependent. (Edit: looks like METR's analysis (Appendix D.1) supports this conclusion, but I'm happy to be corrected here if there is a more careful analysis.)
What do I predict?
In the spirit of sticking my neck out rather than merely criticizing, I will make the following series of point forecasts which I expect to outperform a superexponential fit: just follow an exponential trend, with an appropriate weighting based on recency. If you want to forecast 1 year out, use data from the last year. If you want to forecast 5 years out, use data from the last 5 years. (No doubt it's better to use a decay rather than a cutoff, but you get the idea.) I obviously have very wide error bars on this, but probably not wide enough to include the superexponential fit more than a few years out.
As an important caveat, I'm not making a claim about the real-world impact of an AI that achieves a certain time horizon measurement. That is much harder to predict than the measurement itself, since you can't just follow straight lines on graphs.
Thanks for writing this up! I actually mostly agree with everything you say about how much evidence the historical data points provide for a superexponential-given-no-automation trend. I think I place a bit more weight on it than you but I think we're close enough that it's not worth getting into.
The reason we have a superexponential option isn't primarily because of the existing empirical data, it's because we think the underlying curve is plausibly superexponential for conceptual reasons (in our original timelines forecast we had equal weight on superexponential and exponential, though after more thinking I'm considering giving more weight to superexponential). I think the current empirical evidence doesn't distinguish much between the two hypotheses.
In our latest published model we had an option for it being exponential up until a certain point, then becoming superexponential afterward. Though this seems fairly ad hoc so we might remove that in our next version.
The main thing I disagree with is your skepticism of the meta-skills argument, which is driving much of my credence. It just seems extremely unintuitive to me to think that it would take as much effective compute to go from 1 million years to 10 million years as it takes to go from 1 hour to 10 hours, so seems like we mainly have a difference in intuitions here. I agree it would be nice to make the argument more carefully, I won't take the time to try to do that right now. but will spew some more intuitions.
"We might expect progress in chess ability to be superexponential, as AIs start to figure out the meta-skills (such as tactical ability) required to fully understand how chess pieces can interact. That is, we would expect it to require more new skills to go from an ELO of 2400 to 2500, than it does to go from an ELO of 3400 to 3500."
I don't think this analogy as stated makes sense. My impression is that going from 3400 to 3500 is likely starting to bump up against the limits of how good you can be at Chess, or a weaker claims is that it is very superhuman. While we're talking about "just" reaching the level of a top human.
To my mind an AI that can do tasks that take top humans 1 million years feels like it's essentially top human level. And the same for 10 milion years, but very slightly better. So I'd think the equivalent of this jump is more like 2799.99 to 2799.991 ELO (2800 is roughly top human ELO). While the earlier 1 to 10 hour jump would be more like a 100 point jump or something.
I guess I'm just restating my intuitions that at higher levels the jump is a smaller of a difference in skills. I'm not sure how to further convey that. It personally feels like when I do a 1 hour vs. 10 hour programming task the latter often but not always involves significantly more high-level planning, investigating subtle bugs and consistently error correcting, etc.. While if I imagine spending 1 million years on a coding task, there's not really any new agency skills needed to get to 10 million years, I already have the ability to consistently make steady progress on a very difficult problem.
- My understanding is that AI 2027's forecast is heavily driven by putting substantial weight on such a superexponential fit, in which case my claim may call into question the reliability of this forecast. However, I have not dug into AI 2027's forecast, and am happy to be corrected on this point. My primary concern is with the specific claim I am making rather than how it relates to any particular aggregated forecast.
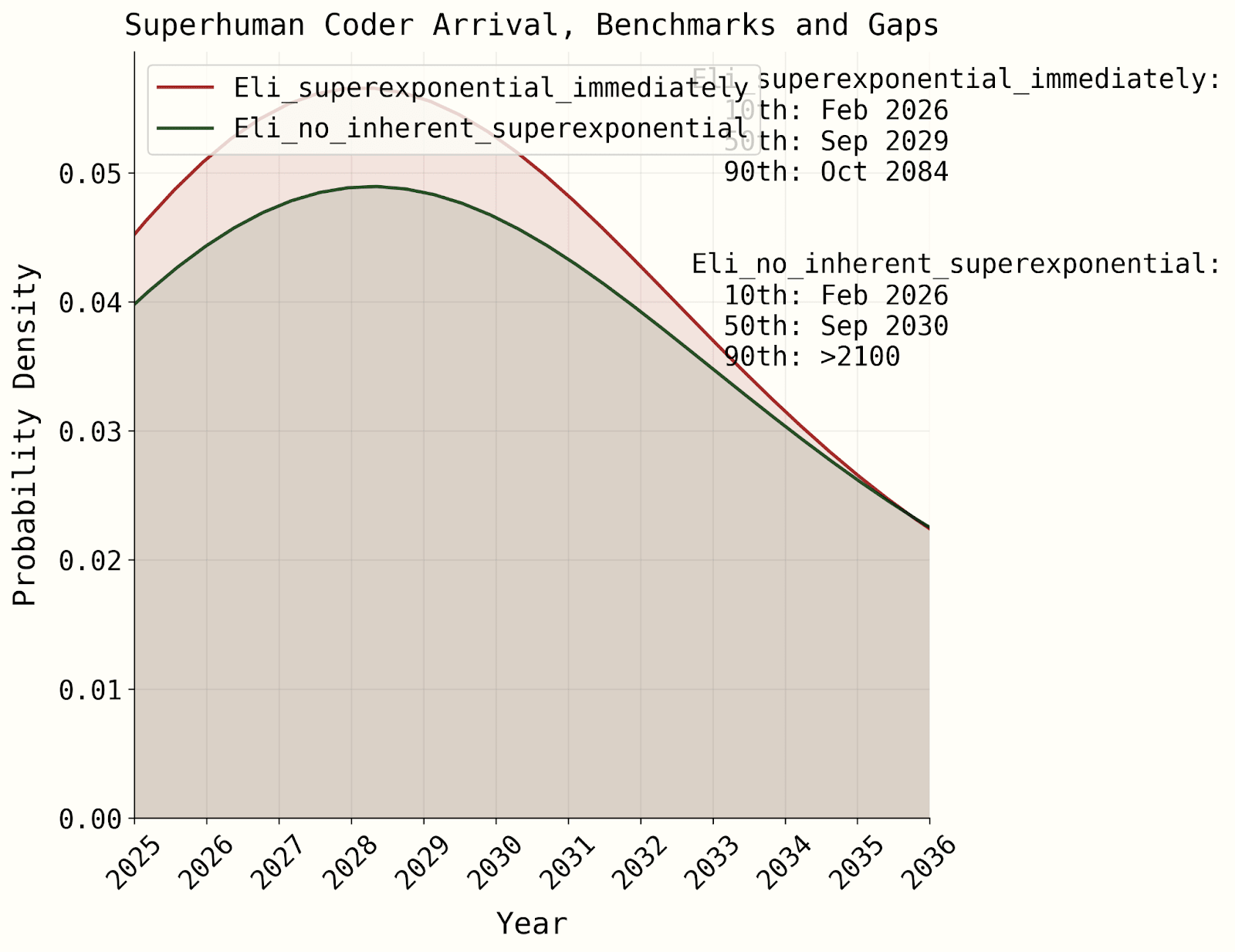
You can see a sensitivity analysis for our latest published model here, though we're working on a new one which might change things (the benchmarks and gaps model relies a lot less on the time horizon extrapolation which is why the difference is much smaller; also "superexponential immediately" is more aggressive than "becomes superexponential at some point" would be, due to the transition to superexponential that I mentioned above):
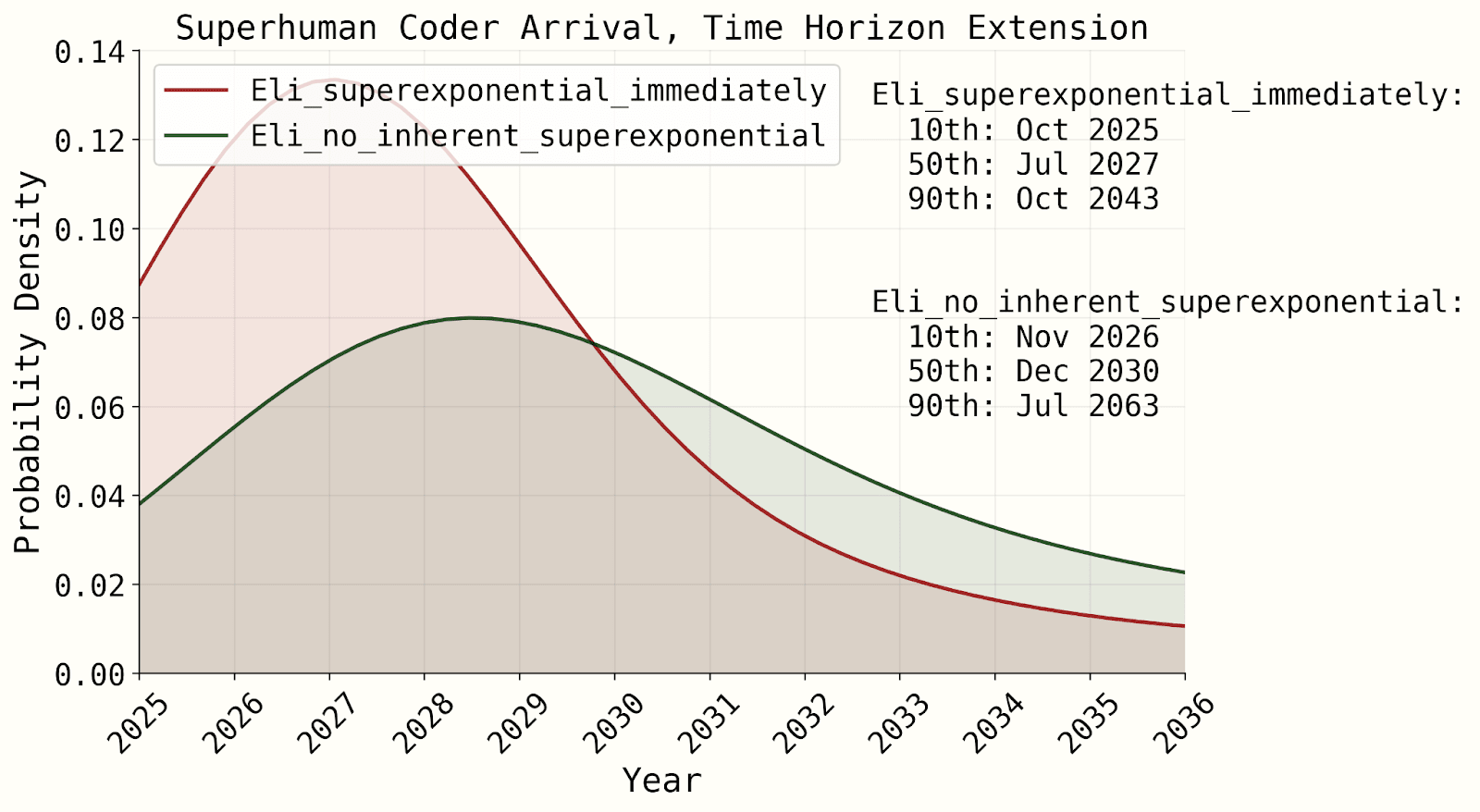
I always thought the best argument for superexponentiality was that (even without AI progress feeding into AI) we’d expect AI to reach an infinite time horizon in a finite time once they were better than humans at everything. (And I thought the “meta skills” thing was reasonable as a story of how that could happen.) This is also mentioned in the original METR paper iirc.
But when AI futures project make that argument, they don’t seem to want to lean very much on it, due to something about the definition. I can’t tell whether the argument is still importantly driving their belief in superexponentiality and this is just a technicality, or whether they think this actually destroys the argument (which would be a major update towards non-superexponentiality to me).
“Another argument for eventually getting superexponentiality is that it seems like superhuman AGIs should have infinite time horizons. However, under the definition of time horizon adapted from the METR report above, it’s not clear if infinite time horizons will ever be reached. This is because AIs are graded on their absolute task success rate, not whether they have a higher success rate than humans. As long as there’s a decreasing trend in ability to accomplish tasks as the time horizon gets longer, the time horizon won’t be infinite. This is something that has been observed with human baseliners (see Figure 16 here). Even if infinite horizons are never reached, the time horizons might get extremely large which would still lend some support to superexponentiality. Even so, it’s unclear how much evidence this is for superexponentiality in the regime we are forecasting in.”
Time horizon is currently defined as the human task length it takes to get a 50% success rate, fit with a logistic curve that goes from 0 to 100%. But we just did that because it was a good fit to the data. If METR finds evidence of label noise or tasks that are inherently hard to complete with more than human reliability, we can just fit a different logistic curve or switch methodologies (likely at the same time we upgrade our benchmark) so that time horizon more accurately reflects how much intellectual labor the AI can replace before needing human intervention.
We're working on updating our timelines in a bunch of ways, and I've thought a bit more about this.
My current best guess, which isn't confident, is that if we took a version of the METR HCAST suite which didn't have any ambiguities or bugs, then the AGIs would have infinite time horizons. And that we should discuss this theoretical task suite rather than the literal HCAST in our timelines forecast, so therefore we should expect a finite time singularity. If we kept the ambiguities/bugs instead we'd have an asymptote and a non-infinite value, as would humans with inifinite time. In the paragraph you're quoting, I think that the main thing driving non-infinite values is that longer tasks are more likely to have ambiguities/bugs that make them unsolvable with full reliability.
I'm happy to talk about a theoretical HCAST suite with no bugs and infinitely many tasks of arbitrarily long time-horizon tasks, for the sake of argument (even though it is a little tricky to reason about and measuring human performance would be impractical).
I think the notion of an "infinite time horizon" system is a poor abstraction, because it implicitly assumes 100% reliability. Almost any practical, complex system has a small probability of error, even if this probability is too small to measure in practice. Once you stop using this abstraction, the argument doesn't seem to hold up: surely a system that has 99% reliability at million-year tasks has lower than 99% reliability at 10 million-year tasks? This seems true even if a 10 million-year task is nothing more than 10 consecutive million-year tasks, and that seems strictly easier than an average 10 million-year task.
Yeah this is the primary argument pushing me toward thinking there shouldn't be a finite-time singularity, as I mentioned I'm not confident. It does feel pretty crazy that a limits-of-intelligence ASI would have a (very large horizon) time horizon at which it has 0.00001% reliability though, which I think is unavoidable if we accept the trend.
I think how things behave might depend to some extent on how you define an achieved time horizon; if there is a cost/speed requirement, then it becomes more plausible that longer horizon lengths would either have ~the same or lower reliability / success rate as smaller ones, once the AI surpasses humans in long-horizon agency. Similar to how if we created a version of HCAST but flipped based on AI times, then at a fixed speed budget human "reliability" might increase at higher time horizons, because our advantage is in long horizon agency and not speed.
In general things seem potentially sensitive to definitional choices and I don't feel like I've got things fully figured out in terms of what the behavior in the limit should be.
I recently gave this talk at the Safety-Guaranteed LLMs workshop:
The talk is about ARC's work on low probability estimation (LPE), covering: