eby Yuxiao Li, Maxim Panteleev, Eslam Zaher, Zachary Baker, Maxim Finenko
July 2025 | SPAR Spring '25
A post in our series "Feature Geometry & Structured Priors in Sparse Autoencoders"
TL;DR: We investigate how to impose and exploit structures across depths and widths in LLM internal representations. Building on the prior two posts about using variational and block/graph priors to control SAE feature geometry, we study 1) Crosscoders with structured priors--i.e., graph- or block-informed reularizations (equivalently Gaussian priors with structured precision) guiding cross-layer alignment--and 2) Ladder SAEs, which introduce multi-resolution sparse bottlenecks to disentangle fine- and coarse-grained concepts within a single model. The goal is to respect nested semantics across depth and scale, reduce polysemanticity, and make representations more interpretable; we summarize what we've implemented, what worked, and key open questions.
About this series
This is the third post of our series on how realistic feature geometry, both categorical and hierarchical ones, in language model (LM) embeddings can be discovered and then encoded into sparse autoencoder (SAE) variants via structured priors.
Series Table of Contents
Part I: Basic Method - Imposing interpretable strctures via Variational Priors (V-SAE)
Part II: Basic Structure - Detecting block-diagonal structures in LM activations
Part III: First Implementation Attempt - V-SAEs with graph-based priors for categorical structure
➡️ Part IV (you are here): Second Implementation Attempt: Crosscoders & Ladder SAEs for hierarchical structure via archictectural priors
Part V: Analysis of Variational Sparse Autoencoders
Part VI: Revisiting the Linear Representation Hypothesis (LRH) via geometirc probes
0. Background Story
The first time we tried to peer inside a language model (LM), it felt like stepping into a library with books scattered on the floor--meaning was everywhere and nowhere. In Part I we started stacking: building toy validation tools and using variational priors with V-SAEs to impose structure. In Part II we noticed that some "genres" naturally cluster, revealing block-diagonal categorical geometry. Part III was a first attempt to control that with graph-informated priors. Now we go deeper: real knowledge isn't flat categories but nested hierarchies--"literature" contains "poetry", chapters sit inside books, themes subdivide into subthemes. This post asks: if concepts live in hierarchies, how should we modify SAE architectures and priors to reflect that? We explore two complementary approaches in parallel: Structured-prior Crosscoders for aligning and tracing concepts across layers, and Ladder SAEs for learning multi-resolution sparse codes inside one model. Together they offer a path toward disentangling hierarchical polysemanticty by respecting layered and nested semantics.
I. Introduction
In the first three installments of this series we moved from raw, tangled representations towards imposed structure: Part I introduced variational SAEs (V-SAEs) to instill interpretable geometry via priors; Part II revealed categorical block-diagonal structure in LM activations; and Part III began controlling that with graph-informed priors. Those efforts treated semanntics largely as flat groupings--"genres" or categories. However, real meaning is also layered. Concepts sit inside hierachies--"topics" refine into subtopics, and representations entangle signals across scales and depth, producing polysemantic directions.
To unpack this layered complexity, we pursue two parallel architectural avenues. The first augments Crosscoders with structured (graph/block/hierarchical) priors to align and trace how concepts propagate across layers, making parent-child transofrmations more transparent. The second introduces Ladder SAEs, which internally decompose activations into multi-resolution sparse codes with consistency ties, separaing fine- and coarse-grained features. Both approaches rely on injecting realistic semantic structure via structured regularization (equivalent to Gaussian priors with precision informed by empirical geometry), offering complementary lenses:
- Crosscoders with structured regularization expose hierarchical re-expression across depth, while
- Ladder SAEs encode hierarchy within a single representation pipeline.
We summarize prior context, position this work relative to existing literature, detail each modeling direction, report current empirical progress on structured-prior crosscoders, and lay out next steps for hierarchical refinements of SAE and their synthesis.
II. Related Work
Linear Representation Hypothesis (LRH), Superpostion & SAEs. The LRH posits that model encode concepts as (approximately) linear directions; superposion explains polysemanticity via many features sharing limited neurons. See Anthropic's Toy Models of Superposition for the LRH/superposition framing. SAEs aim to recover monosemantic directions by sparse dictionary learning over activations; recent scaling and training improvements expand coverage and stability. Key references include, Towards Monosemanticity (2023), Scaling and Evaluating Sparse Autoencoders (2023) for training/scaling insights, and concerns about "dictionary worries" and absorption (2023) issue.
Feature geometry. Empirical work increasingly suggests that LM activations organize into categorical blocks (low-dimensional subspaces with high intra-category similarity) that are nested hierarchically across concepts and layers. In our Part II post we decoumented block-diagonal structure and simple probes that reveal it, and collected pointers to word-vector analogies and linear relational structure that foreshadow such geomtry.
Cross-layer alignment & Crosscoders. Crosscoders learn sparse correspondences across layers and support model diffing. Key works include Cross-Layer Features and Model Diffing (2024) and Insights on Crosscoder Model Diffing (2025) We build on this structure by adding structured priors to encode semantic relations during alignment.
Deep SAEs & probe complexity. Multi-layer/Deep SAEs seek hierarchical latents via stacked sparse bottleneck; debate centers on gains vs. risk of non-linear "hallucinated" features and probe complexity, discussed in Deep SAEs yield interpretable features too (LW) and matching-pursuit/ITDA directions.
III. Modeling
Shared notation
- What we mean by hierarchy. A representation can be "hierarchical" in two orthogonal senses:
- Across-depth transport (parentchild): A concept at layer is re-expressed at +1 (e.g., refined, specialized). We want this transport to preserve semantic neighborhoods and category structure. (Handled by Crosscoders with structured priors)
- Within-layer scale (coarsefine): Some features explain very local, fine patterns; others summarize broader, coarse patterns. (Handled by Ladder SAEs)
- Why both? Crosscoders align transport so semantic neighborhoods survive through depth. Ladder SAEs separate scales so features stop competing across granularity. Both use the same structured prior toolkit (graph/block), but at different loci.
3.1 Crosscoders with Structured Priors (Cross-Depth Hierarchy)
Goal. Preserve who-is-near-whom as a concept transports from layer to by imposing a structure-respecting prior on the latent codes of a crosslayer mapper. We follow the variational framework from Part I and make the efficient penalty we actualy train with explicit.
3.1.1 Variational formulation
Let be the target, the conditioning input, and latent. Encoder , decoder , prior .
The (negative) ELBO reads
Choose Gaussian families posterior , and a structured Gaussian prior
,
where L is the Laplacian of a similarity graph over latent dimensions (token/sentence/category). Then
Deterministic limit. If we take (or ), the KL contributes . Over a batch withrows :
with , this becomes the Laplacian quadratic that enforces smoothness over the chosen graph. The isotropic prior, mentioned in Part I as an easier starter, is the special case (we observed poorer alignment with that baseline due to the misalignment).
3.1.2 Two equivalent deterministic forms
For a single vector :
For a batch :
Hence the pairwise-difference penalty and the Laplacian quadratic are identifcal up to constants; the former is mini-batch friendly and avoids materializing .
3.1.3 What we actually training (programmer-friendly)
We use a deterministic crosscoder spine, plus a pairwise penalty. Specifically, suppose the encoder and the decoder are both deterministic approximations. Encoder maps inputs to latents ; decoder maps latents back, i.e., . Batch of latents: (rows = batch of examples, cols = latents).
We approximate the likelihood term via the reconstruction:
We define Graphs live over latent dimensions (token/sentence/category edges). Let be a symmetric similarity (k-NN) matrix over latent indices (in practice E5 kNN ), its Laplacian. We define the pairwise form:
Penalties of the form are equivalent to from the variational derivation.
Thus, the total loss is combined by the reconstruction loss, the graph penalty, and a sparsity penalty as follows,
(optional)
Table 1: Comparison of different graph penaly terms.
| Method | Objective term (per batch) | Inputs you need | Batch complexity (rough) | Strengths | Weaknesses | Equivalence / Notes |
|---|---|---|---|---|---|---|
| Variational structured prior (KL) | , with | posterior , prior precision from graph/Laplacian. | diagonal full |
|
| deterministic limit () → Laplacian quadratic. |
| Laplacian quadratic (dense) | dense Laplacian | matmul |
|
| Equal to if | |
| Pairwise difference (dense) | Dense adjacency (symmetrized) |
|
| Exactly equal to Laplacian quadratic up to constants | ||
| Pairwise difference (sparse edge-list) | (current implementation) | Edge list (e.g., kNN) with weights , ideally symmetrized |
|
| Same as dense pairwise when covers the nonzeros of |
Practical tips
- Symmetrize (e.g., ); consider degree normalization.
- Pick kNN so balances compute vs. quality; prefer edge-list for big .
- Sweep and check (i) recon vs sparsity; (ii) feature-feature heatmaps; (iii) NDCG/Precision on neighborhood recovery.
3.2 Ladder-SAEs (Cross-Width Hierarchy)
Goal. Crosscoders regularize transport across depth so semantic neighborhoods survive layer-to-layer. Ladder SAEs regularize decomposition across scale within the same layer, so fine patterns don't fight with coarse ones, reducing polysemantic overlap within a layer. Both impose the same structure-respecting bias (sparsity + simple consistency constraints, optionally graph priors).
Inituition. Real representations mix granularities (morphemes/lexical motifs topics/styles). A single sparse layer often blends them (polysemanticity). A ladder allocates separate sparse capacity to each granularity and ties levels together so each level explains what it should--no more, no less.
Minimal design:
Encoder (L levels, ):
Decoder with ladder ties:
Loss (same backbone + sparse/consistency at each scale):
where is the level-wise consistency which prevents free-form nonlinearity, and each level must reconstruct its own view; is the level-wise sparsity, which typically stronger at fine scales.
To get the exact parallel to crosscoders, we can add per-level graph penalties as well, representing as:
e.g., we can set token kNN at level-1, and category/block graphs at coarser levels, encoding that blocks get bigger as scale grows.
Benefits:
- Scale separation fewer mixed latents. Fine features specialize; coarse features summarize.
- Faithfulness guardrails. Consistency terms make it costly to "hallucinate" features: each level must explain itself and the input.
- Unification with the series. Same reconstruction spine; same regularizer family (sparsity + graph/Laplacian or its variational cousin); just applied within-layer rather than across-depth.
IV. Experimental Results (so far: Crosscoders)
4.1 Crosscoders with grah-based regularization
4.1.1 Setup
- Task & data.
- Cross-layer feature alignment on GPT-2 (global, acausal crosscoder) using TinyStories train/test.
- Model variants.
- Vanilla Crosscoder (Vanilla): .
- Crosscoder with isptropic Gaussian prior (Gaussian-iso):
- Crosscoder with sentence-level graph (Graph): (sentence-level graph).
- Graph construction.
- Sentence embeddings via E5; neighbors via FAISS (top-256); no graph-aware batching in these runs.
- Optimization. AdamW; linearly increased at the beginning to emphasize reconstruction.
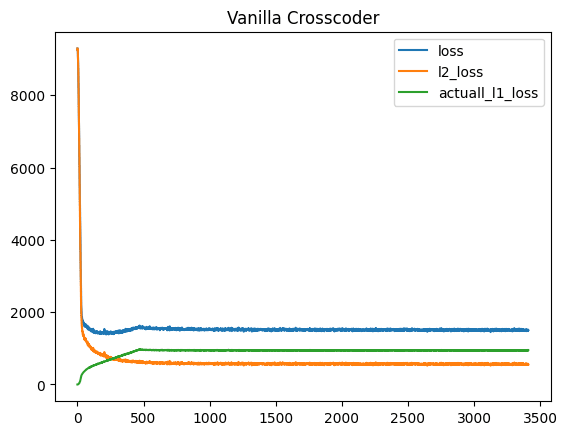
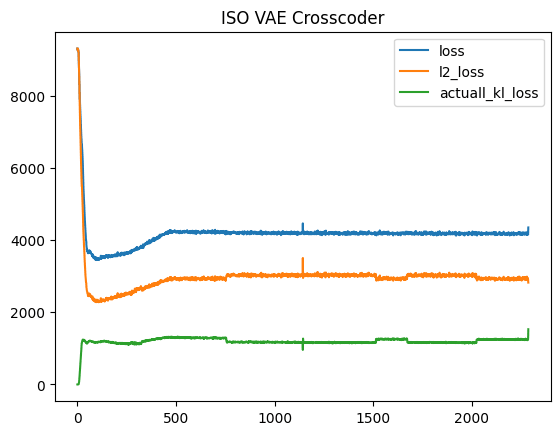
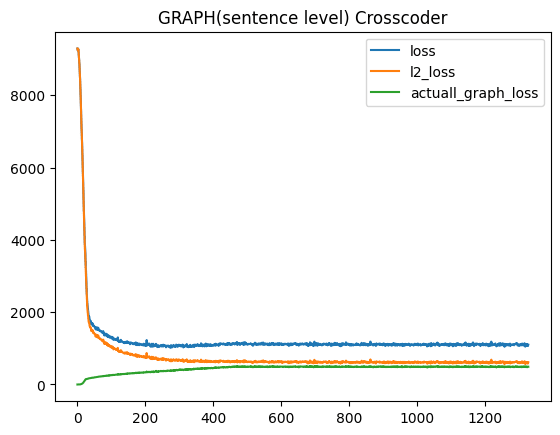
According to the training curves, all three configurations show stable convergences. The representative loss trajectories are provided as follows,
Fig. 1: Training loss curves for Vanilla, Gaussian-iso, Graph Crosscoders showing stable convergence ad final plateaus.
4.1.2 Evaluation metrics and quantitative results
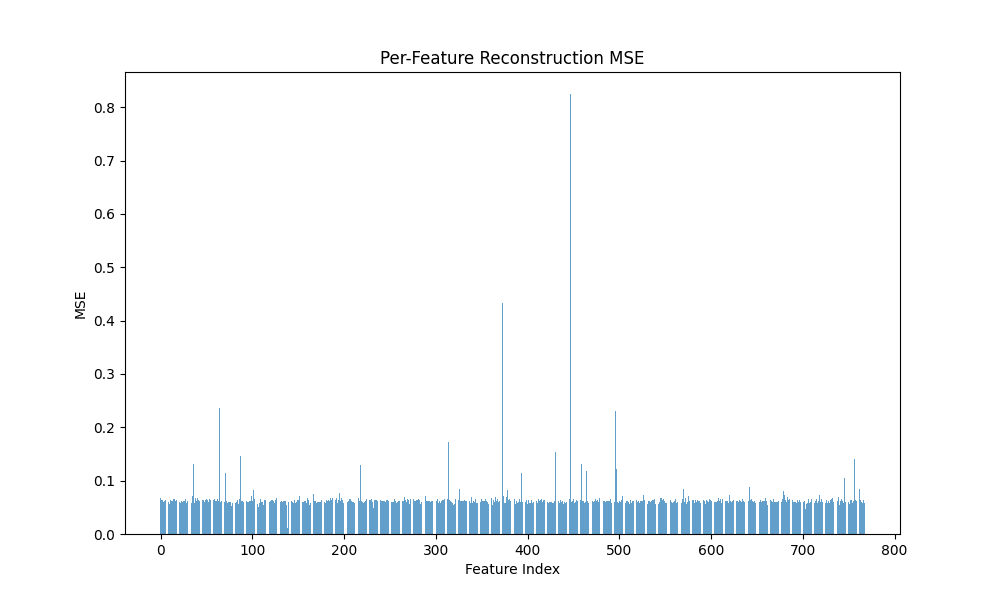
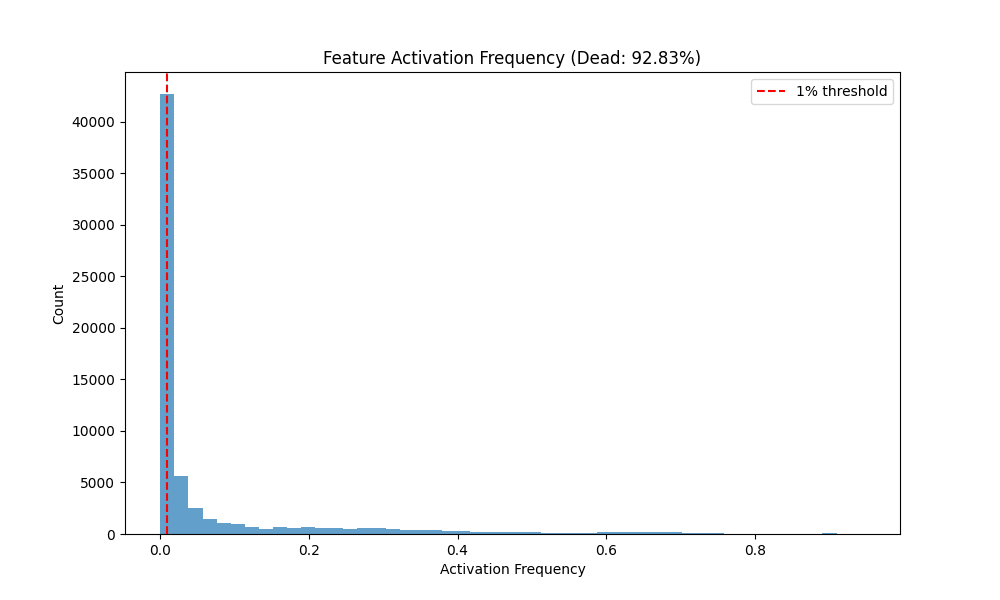
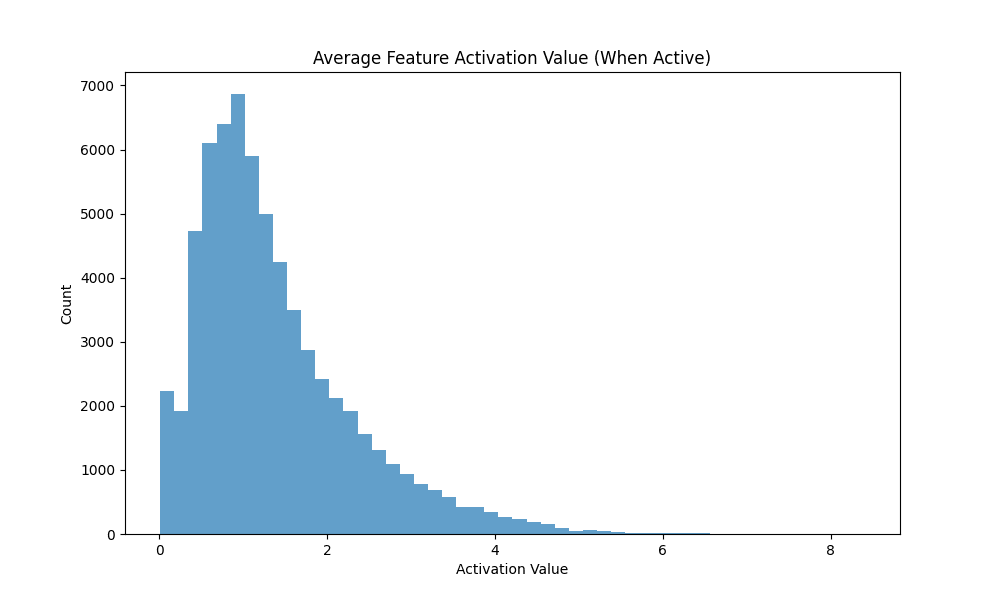
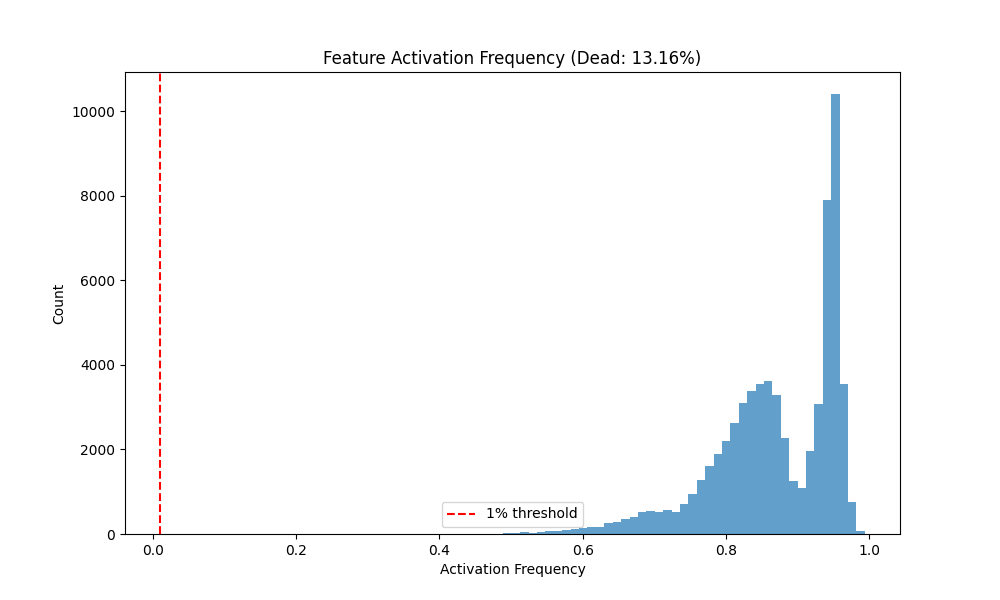
- Reconstruction & sparsity: We report Batch MSE and (fidelity) plus Dead % (fraction of latents never firing), Activation Frequency (AF), and Activation Value (AV) (sparsity profile). Better lower MSE, higher , higher sparsity (to a point) without collapsing capacity.
- Neighborhood recovery (structure similarity): We utilize the sentence-graph as "ground-truth" neighborhoods, where we measure how well latent geometry preserves that structure via Precision@k (fraction of retrieved k neighbors that are true neighbors) and NDCG@k (ranking-sensitive match). Better higher values; indicates the learned latents respect the external semantic graph.
Table 2: Reconstruction & sparsity on the test set
| Model | Dead % | Median AF | Mean AF | Mean AV | Neuron MSE | Batch MSE | R² |
|---|---|---|---|---|---|---|---|
| Vanilla / L1 | 92.83 | 0.008996 | 0.07166 | 1.38788 | 0.0600 | 556.27 | 0.9401 |
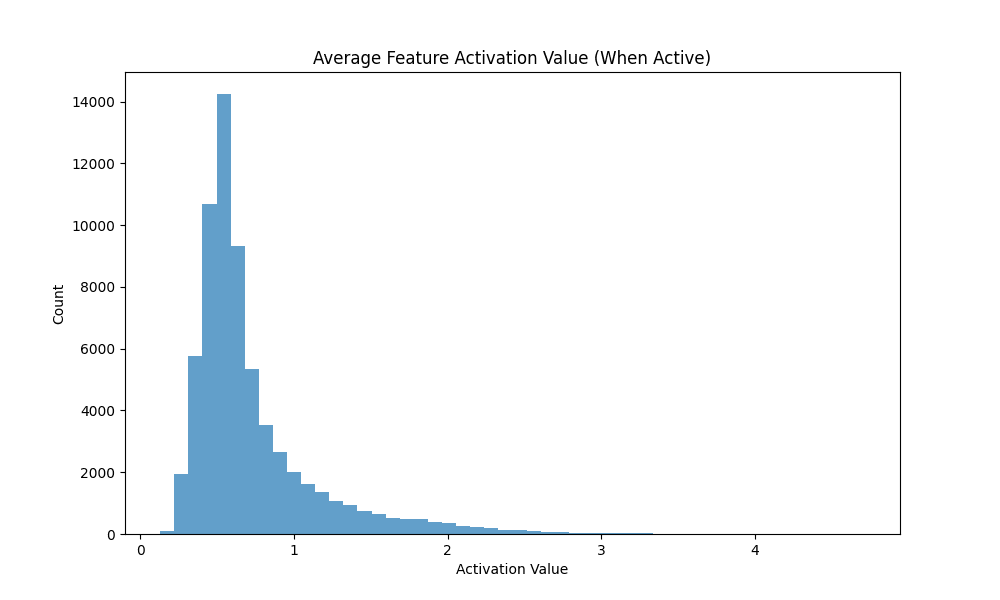
| Gaussian-iso | 13.16 | 0.87490 | 0.86800 | 0.04600 | 0.3150 | 2905.33 | 0.6870 |
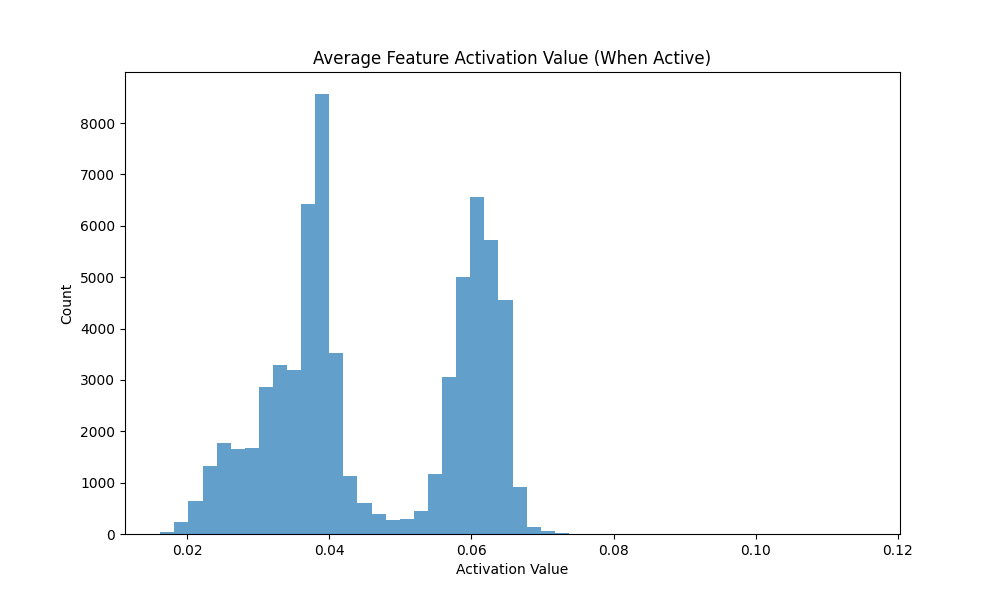
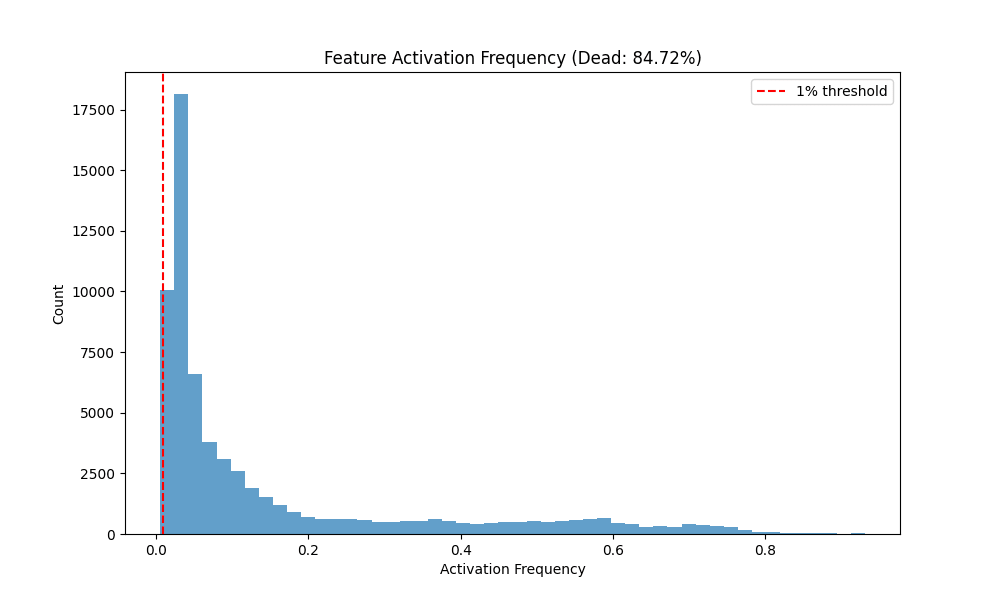
| Graph | 84.72 | 0.05423 | 0.15276 | 0.72870 | 0.0658 | 606.61 | 0.9347 |
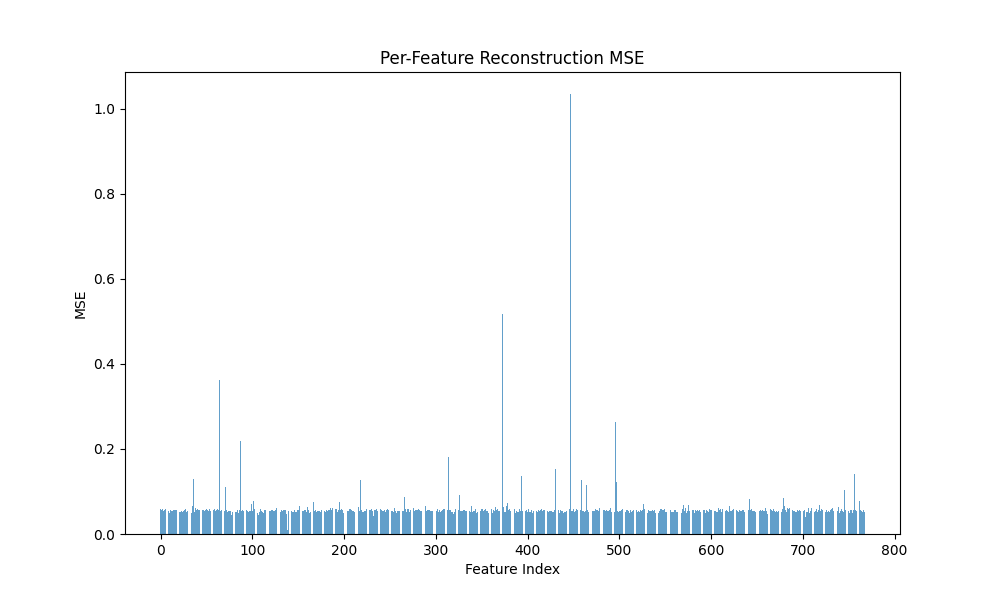
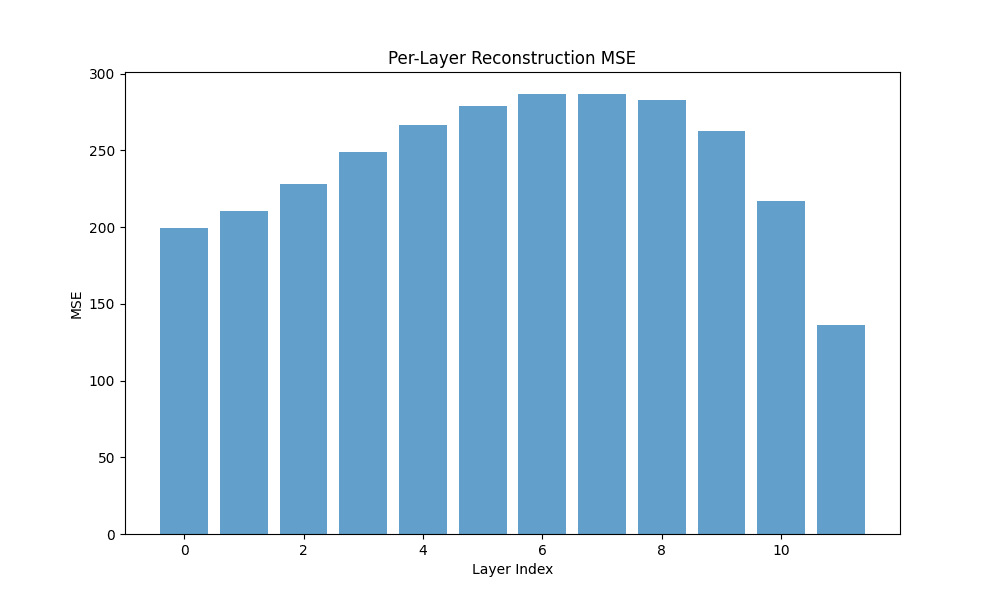
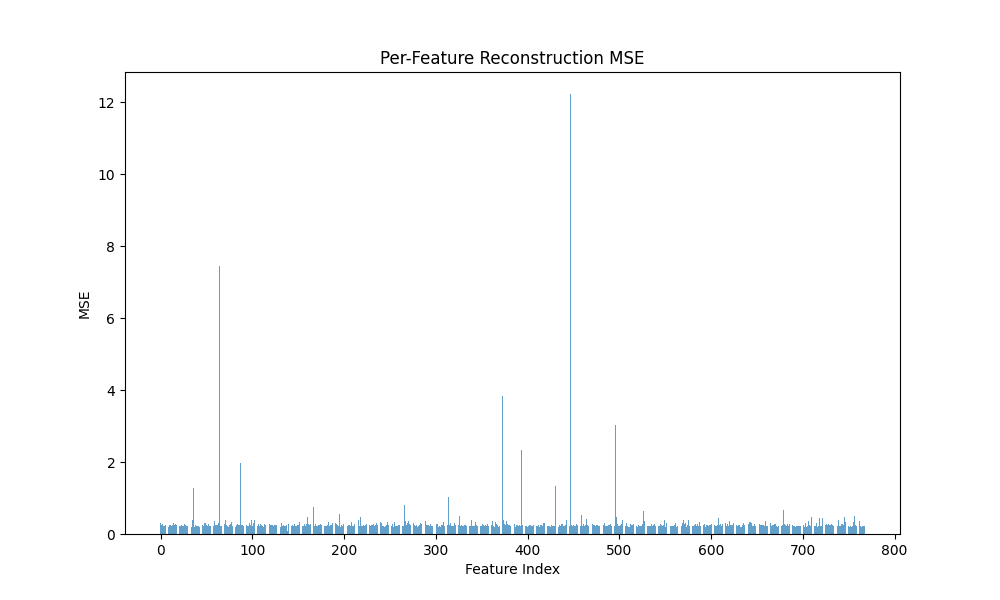
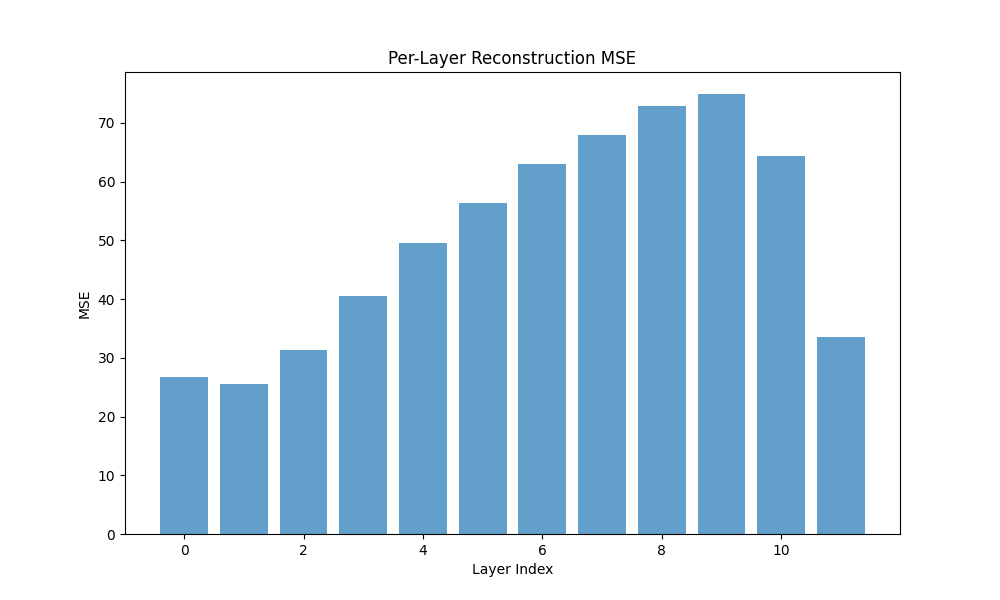
Observations. Vanilla and Graph achieve comparable and high fidelity (0.940 vs 0.935) with low MSE, while Gaussian-iso lags on both fidelity and sparsity. Notably, Graph reaches substantial sparsity without (Dead 84.7%), whereas Vanilla with is even sparser (Dead 92.8%).
Implications. A structured penalty can substitute for to induce sparse, high-fidelity latents. Isotropic priors, on the other hand, do not provide the right inductive bias for this task.
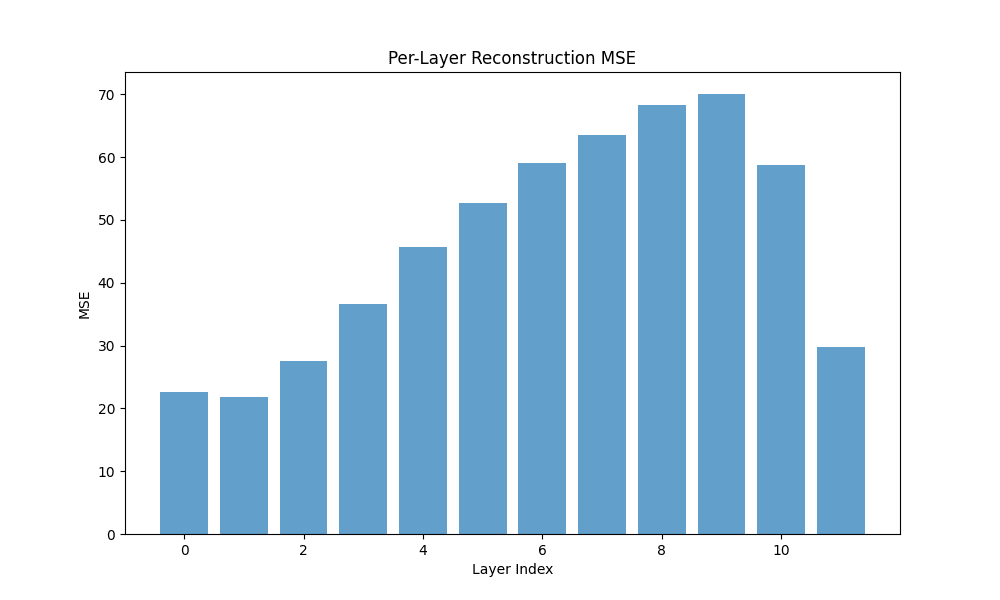
(a) Vanilla Crosscoder MSE
(b) Gaussian-iso Crosscoder MSE
(c) Graph Crosscoder MSE
Fig. 2: Bars for Batch MSE by model
(a) Vanilla Crosscoder Sparsity
(b) Gaussian-iso Crosscoder Sparsity
(c) Graph Crosscoder Sparsity
Fig. 3: Sparsity diagnostics (Dead %, AF/AV) across models
Neighborhood recovery (sentence-graph)
| Model | NDCG@64 | NDCG@128 | NDCG@256 | Prec@64 | Prec@128 | Prec@256 |
|---|---|---|---|---|---|---|
| Vanilla / L1 | 0.21274 | 0.17952 | 0.14804 | 0.01289 | 0.02350 | 0.05469 |
| Graph | 0.20912 | 0.17677 | 0.14610 | 0.01340 | 0.02355 | 0.05284 |
Observations. Graph yields higher Precision@64 (0.01340 vs 0.01289), i.e., more true neighbors at the top; parity at @128; slightly lower at @256. Vanilla shows marginally higher NDCG across k.
Implications. The Graph regularizer better preserves local semantic neighborhoods (top-k precision), consistent with its smoothness bias. The small NDCG edge for Vanilla is likely an artifact of asymmetric kNN graphs (FAISS); symmetrizing WWW or using degree-normalized Laplacians should close this gap. Overall, the graph-regularized crosscoder demonstrably aligns latent geometry with the external sentence graph.
4.1.3 Discussion: why Gaussian-sio underperforms, and why Graph succeeds
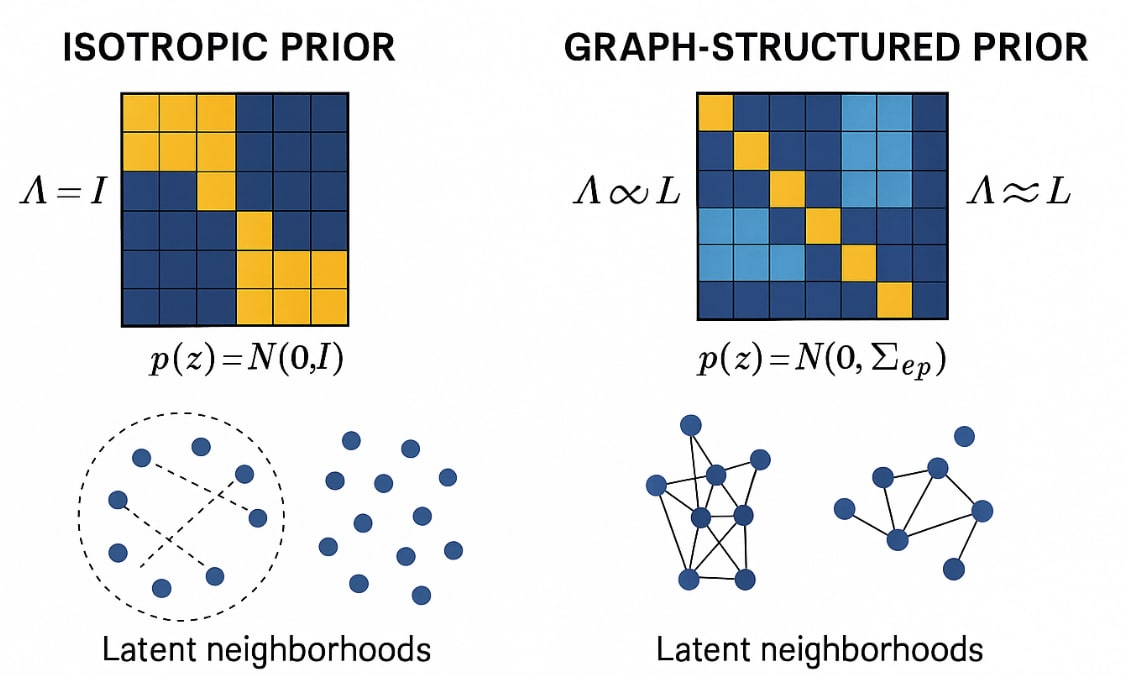
In short, it's not a variational vs deterministic issue. The gap stems from prior specificiation, not from the presence/absence of a KL term. Gaussian-iso imposes , a rotation-invariant pessure that ignores empirical adjacency (sentence/token/category neighborhoods). Its KL term therefore pulls against the true graph structure, degrading fidelity and sparsity in this setting. By contrast, the Graph penalty is the deterministic limit of a Gaussian with structured covariance: with precision . This matches the data's neighborhood geometry and explains its performance. The fair variational comparator is a Gaussian-structured KL (precision ), which we expect to recover or exceed the Graph results at similar compute.
4.1.4 Next steps (ongoing)
- Better graphs: symmetric kNN; degree-normalized ; combine token + sentence + category graphs for multi-scale structure.
- Graph-aware training: edge sampling; periodic neighbor refresh; ablations.
- Constraint combinations: Graph + small to probe synergy on the recon–sparsity Pareto frontier.
- Variational parity: swap Gaussian-iso for a Gaussian-structured KL (precision ); compare to deterministic Graph at matched compute.
- Scale & eval: larger LMs/datasets; SAE-bench style metrics; parent→child probes across layers to quantify hierarchy preservation.
4.2 Ladder SAEs
Since the results here are still pending, we'll briefly introduce how we schedule to validate the performance of Ladder SAEs:
- Per-level heatmaps of feature-feature correlation: small blocks (fine) nesting into larger blocks (coarse).
- Cross-level correspondence: a coarse unit should reliably recruit a small set of fine units.
- Coherence and per level vs a single-layer SAE with matched total capacity.
V. General Next Steps
- Ladder SAE experiments (planned): toy manifolds and real LM activations, visualization of nested clusters, coherence/disentanglement metrics.
- Combining hierarchies: how crosscoders and ladder SAEs complement each other in resolving polysemanticity.
- Structured priors fusion: block + hierarchical priors (semantic categories within coarse/fine scopes).
- Scaling & evaluation: larger models/domains, hierarchy-preserving generalization, parent-child fidelity probes.
- Open hypotheses & community input: metrics, failure modes, integrating causal probing.
VI. Conclusion
In this post we added the aisles and floor plan: "cross-latyer maps" (Crosscoders with structured priors) that keep nearby books near each other as you move deeper through the stacks, and "within-shelf organization" (Ladder SAEs) that separates fine-grained pamphlets from broad anthologies so they don't get jammed into the same slot. Together, these give us a practical recipe for taming hierarchical polysemanticity: Crosscoders preserve neighborhoods through depth; Ladder SAEs disentanfle granularities within a layer--two complementary levers, one unified framework.
Call to action.
- Experiment: try the graph-regularized crosscoder (token/sentence/category graphs), and prototype ladder SAEs with per-level sparsity + consistency.
- Build on it: swap in structured Gaussian priors, combine graph + small L1, scale to bigger LMs, add "parent→child" probes.
- Critique: stress-test failure modes (absorbed features, graph mis-specification, batch bias), propose better metrics for hierarchy preservation.
- Collaborate: share graphs, configs, and results—especially block-diagonal/category priors and ladder visualizations.
If the library metaphor is right, we’re getting close to a catalog you can actually navigate. Let’s finish the map together!
References
[1] Gemma Scope: Open Sparse Autoencoders Everywhere All At Once on Gemma 2
[2] Scaling Monosemanticity: Extracting Interpretable Features from Claude 3 Sonnet
[3] Graph Regularized Sparse Autoencoders with Nonnegativity Constraints
[4] Peter Gao, Nelson Elhage, Neel Nanda, et al. Scaling sparse autoencoders. Anthropic, 2024
[5] Revisiting End-To-End Sparse Autoencoder Training: A Short Finetune Is All You Need
[7] Text Embeddings by Weakly-Supervised Contrastive Pre-training