Sparse Autoencoders (and other related feature extraction tools) often optimize for sparsity to extract human-interpretable latent representations from a model's activation space. We show analytically that sparsity naturally leads to feature absorption in a simplified untied SAE, and discuss how this makes SAEs less trustworthy to use for AI safety with some ongoing efforts to fix this. This might be obvious to people working in the field - but we ended up writing a proof sketch so we're putting it out here. Produced as part of the ML Alignment & Theory Scholars Program - Winter 2024-25 Cohort.

The dataset (a distribution with feature hierarchy)

In this proof, we consider a dataset $D$ with points sampled to exhibit features from a set of feature $F=\{f_1,f_2,f_3,\cdots ,f_d\}$. Particularly, we will consider two features $(f_1,f_2)$ that follow the hierarchy $f_2\subset f_1$ (think f_2 = elephant and f_1 = animal for instance), where existence of  $f_2$ implies existence of $f_1$. 

Hierarchy in human-interpretable features is prevalent (and hard to study in LLMs). While other unrelated features still exist, for $f_1$ and $f_2$, we can partition the probability of this dataset for four combinations:

So these are the individual probabilities of a datapoint eliciting these combinations of features:

• $p_{11}\equiv p_{f_1,f_2}$ (both features present, think elephant, which implies animal),
• $p_{10}\equiv p_{f_1,\neg f_2}$ (only $f_1$ present, think cat or dog)
• $p_{01}\equiv p_{\neg f_1,f_2}$ (only $f_2$ present, which should be zero, because of hierarchy)
• $p_{00}\equiv p_{\neg f_1,\neg f_2}$ (neither feature present, maybe talking about volcanoes)

Each feature $f\in R^d$ is a vector with unit norm, and we assume that all features are mutually orthogonal, so $f_a\cdot f_b=0\forall f_a,f_b\in F$. Each activation $h\in R^d$ in the model's residual stream is a sum of all active features.

Training a Sparse Autoencoder (SAE)

Given a language model with residual stream activations $h\in R^d$, the sparse autoencoder learns a mapping $f_{\varphi }$ such that  $\hat{h}=f_{\varphi }\left(h\right)$ reconstructs $h$. The total loss consists of a reconstruction term $L_{\text{rec}}$, which minimizes the squared error, and a sparsity term $L_{\text{sp}}$, enforcing sparsity via an $L_p$-norm penalty on $\hat{h}$. The model parameters $\varphi$ are optimized   via gradient descent to minimize $L$. The complete loss:

where $L_{\text{rec}}=E_{x\sim D}[\parallel \hat{h}-h{\parallel }_2^2]$  (the reconstruction loss) and $L_{\text{sp}}=E_{x\sim D}\left[\lambda {\sum }_i|{\hat{h}}_i{|}^p\right]$ (the sparsity loss).

The SAE constructs latent activations $\hat{h}$ as $\hat{h}=W_{d}z$, where $z=ReLU\left(W_{e}h\right)$.

We consider encoders and decoders without biases for simplicity, and we look at the latents of the SAE that are related to the two features $f_1$ and $f_2$, and show that absorption doesn't affect reconstruction and increases sparsity, and that optimizing for sparsity pushes for higher absorption.

Evaluating the SAE loss under $\delta$-absorption

We use $z_i$ to denote the hidden activation for latent $i$, $e_i$ to denote the SAE encoder for latent $i$, and $d_i$ to denote the SAE decoder for latent $i$. We assume the decoder is linear, that is, the reconstruction $\hat{h}$ is a linear combination of latents $\hat{h}={\sum }_i{d}_i{z}_i$. We assume that the first $2$ latents ($z_1$ and $z_2$) track $f_1$ and $f_2$ without loss of generality.

We define $\delta$-absorption as part-way between no absorption ($\delta =0$) and full absorption ($\delta =1)$. Thus, $e_1=f_1-\delta f_2$, $e_2=f_2$, $d_1=f_1$, and $d_2=f_2+\delta f_1$, and we look at the reconstruction and sparsity losses under varying amounts of absorption.

Reconstruction under $\delta$-absorption

Case 1:  $h=f_1$ (parent feature only)

In this case, the parent feature fires on its own, so the SAE just needs to reconstruct $f_1$. 

The first latent fires with magnitude 1, since $f_1\cdot f_1=1$ but $f_1\cdot f_2=0$ since $f_1\perp f_2$ .

The second latent fires with magnitude 0 since $f_1\cdot f_2=0$..

The decoder output is thus just $f_1$, perfectly reconstructing the input.

Case 2:  $h=f_1+f_2$ (parent and child together)

In this case, the parent and child are firing together, so the SAE needs to reconstruct the sum of the parent and child features $f_1+f_2$.

The first latent fires with magnitude $1-\delta$ since $f_1\cdot f_1=1$ and $f_2\cdot f_2=1$, but $f_1\cdot f_2=0$ since $f_1\perp f_2$. We have $z_2=\text{ReLU}\left(f_{2}z\right)=\text{ReLU}\left(f_2\right(f_1+f_2\left)\right)=1$.

The second latent fires with magnitude 1 since $f_2$ is present in $h$.

The decoder output sums to $f_1+f_2$, again perfectly reconstructing the input.

Case 3:  $h=0$ (nothing fires)

Here, $z_1=\text{ReLU}\left(\right(f_1-\delta f_2\left)h\right)=0$ and $z_2=\text{ReLU}\left(f_{2}z\right)=0$.

When neither feature is present, neither latents fire:

And thus the decoder output is still 0, achieving perfect reconstruction.

We do not need to consider the case where $f_2$ fires alone, as this is not allowed by our absorption setup. As we see above, in all cases, any level of absorption $\delta$ still achieves perfect reconstruction.

Intuitively, absorption does not hinder reconstruction because knowing the elephant feature is active is enough to infer animal even if that feature gets absorbed.

Sparsity under $\delta$-absorption

We calculate the sparsity loss as follows:

where $h=\{f_1^{\prime },f_2^{\prime }\}$ represents the two features that are related to $f_1$ and $f_2$, and $L_n$ is the norm (to disambiguate with $p$). Since the representation and sparsity of the unrelated features stays the same, we look at this value of sparsity and how it changes with the amount of absorption in our data distribution.

Case 1: $\delta =0$ (no absorption)

With no absorption (which means the SAE learned the true features $f_1$ and $f_2$ in both the encoder and decoder), the sparsity comes out to be (with $n$-norm, where we assume $f_{enc}\in \{0,1\}$ for simplicity):

Case 2: $\delta =1$ (absolute absorption)

With absolute absorption of a feature (all datapoints exhibiting it), with the decoder learning $f_2$ and $f_2+f_1$ respectively for the encoder features $f_1\setminus f_2$ (exclusion due to absorption) and $f_2$. In this case, we get the following sparsity loss:

Case 3: General Case (some $\delta$ amount of absorption)

Finally, with an arbitrary amount of absorption of $f_1$ into $f_2$, we get:

It is evident that absorption leads to higher sparsity in encoder activations for hierarichical features. Now, we show that minimizing sparsity via differentiating naturally leads to increasing absorption.

Differentiating the Sparsity Loss

Assume that the sparsity penalty is given by an $L_n$ norm on the encoder activation: 

We can see that the derivative of the $L_p$ sparsity loss with respect to $\delta$ promotes absorption:

This derivative is always negative as long as $p_{11}>0$, i.e., datapoints with both features exist in our distribution, so increasing sparsity (decreasing the loss) always increases absorption. Next, we show that absorption makes SAEs (and other related feature extractions) much less trustworthy for safety.

Absorption makes SAEs less trustworthy for safety

The hope with SAEs (and other related research) is that we extract model-internal latents representing human-interpretable features that we can detect and control. For this to be usable, we want this to work successfully for complex, harmful behaviours such as lying, strategic deception, power-seeking, sycophancy, backdoors, etc.

Absorption, and sparsity in feature-extraction which promotes absorption, means that even if we find linear latents for these features (for which we don't really have good progress in the first place [TODO: cite], we can't trust them.

A feature for deception, with absorption, might actually have learned deception-except-deception-in-2027, or a feature with power seeking might have learned power-seeking-except-instrumental-convergence. Unless we fix our feature extractors to not optimize to maximise just sparsity in latent activations (some other ideas and starting points include KL-divergence and parameter-space related directions), we can't trust our SAEs, and their features can potentially be more misleading and harmful than helpful.

An example of feature absorption in real-world models

In the original feature absorption paper, absorption is shown to occur in real SAEs trained on LLMs. SAE latents that seem to track starting letter information (e.g. a feature that fires on tokens that start with $S$) fails to fire on seemingly arbitrary tokens that start with (like the token "_short"). The paper shows that this is due to more specific latents "absorbing" the "starts with $S$" direction.

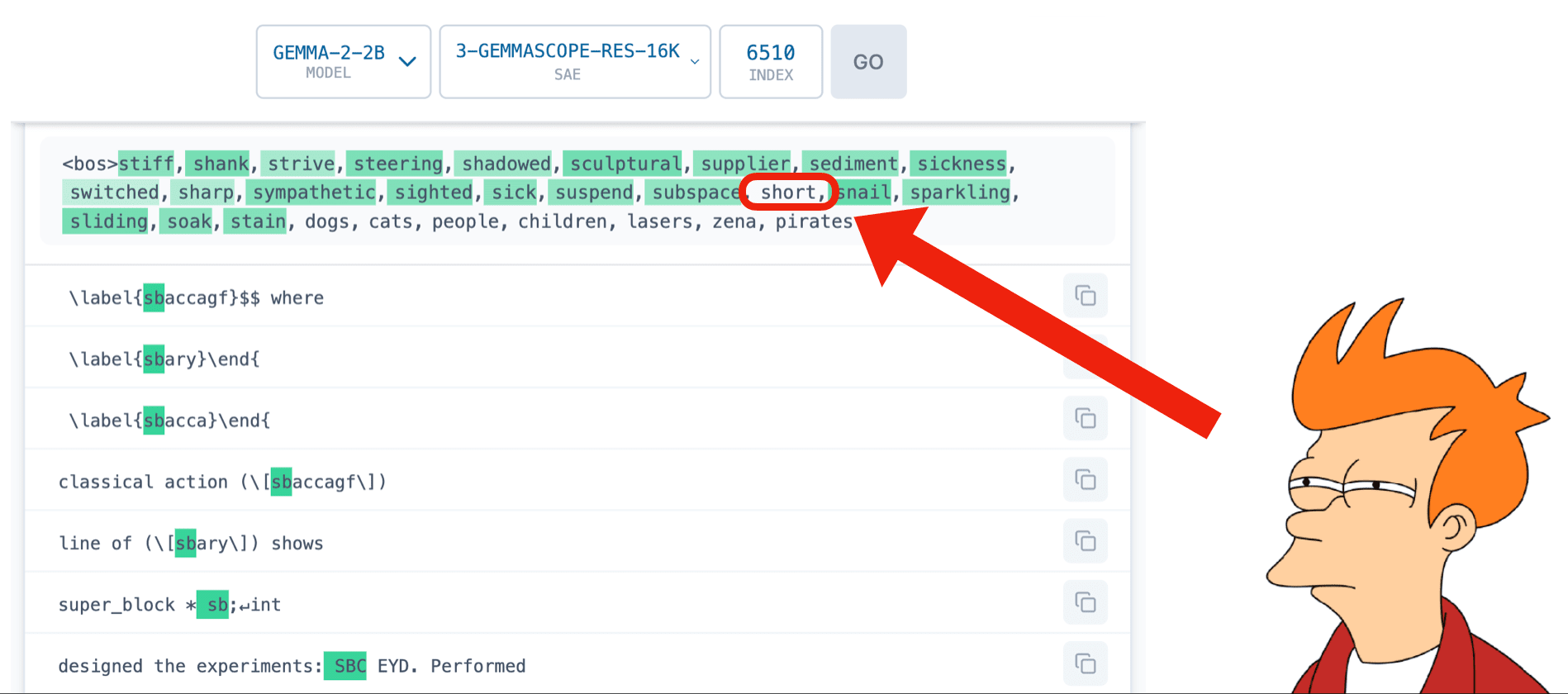
The original paper hypothesizes that feature absorption is a logical consequence of the sparsity penalty in SAE training, but we now have a proof that naively optimizing an SAE for sparsity will indeed lead to feature absorption.

How much of this applies to other SAE variants and feature-extraction methods?

We should expect feature absorption in any SAE architecture that incentivizes sparsity, which at present is all common architectures. JumpReLU, TopK, and standard L1 SAEs all extract feature representations by making use of sparsity and we should thus expect them all to engage in feature absorption.

Cross-layer SAE variants such as crosscoders^[1] and transcoders^[2] also rely on sparsity to extract features and we should thus also expect that these new architectures will also suffer from feature absorption. Indeed, recent work on transcoders finds they do experience feature absorption^[3].

Matryoshka SAEs to fix Absorption

Matryoshka SAEs are a promising approach to fixing absorption in SAEs. These SAEs encode a notion of hierarchy by forcing earlier latents to reconstruct the full output on their own, making it more difficult for parent latents to have holes in their recall for child features.

1. ^{^}

   Sparse Crosscoders for Cross-Layer Features and Model Diffing [link], Jack Lindsey, Adly Templeton, Jonathan Marcus, Thomas Conerly, Joshua Batson, Christopher Olah, Transformer Circuits Thread 2024

2. ^{^}

   Transcoders Find Interpretable LLM Feature Circuits [link], Jacob Dunefsky, Philippe Chlenski, Neel Nanda, arXiv:2406.11944, 2024

3. ^{^}

   Transcoders Beat Sparse Autoencoders for Interpretability [link], Gonçalo Paulo, Stepan Shabalin, Nora Belrose, arXiv:2501.18823, 2025