Hey Jacob + Philippe,
Hope you all don't mind but we put up layer 8 of your transcoders onto Neuronpedia, with ~22k dashboards here:
https://neuronpedia.org/gpt2-small/8-tres-dc
Each dashboard can be accessed at their own url:
https://neuronpedia.org/gpt2-small/8-tres-dc/0 goes to feature index 0.
You can also test each feature with custom text:
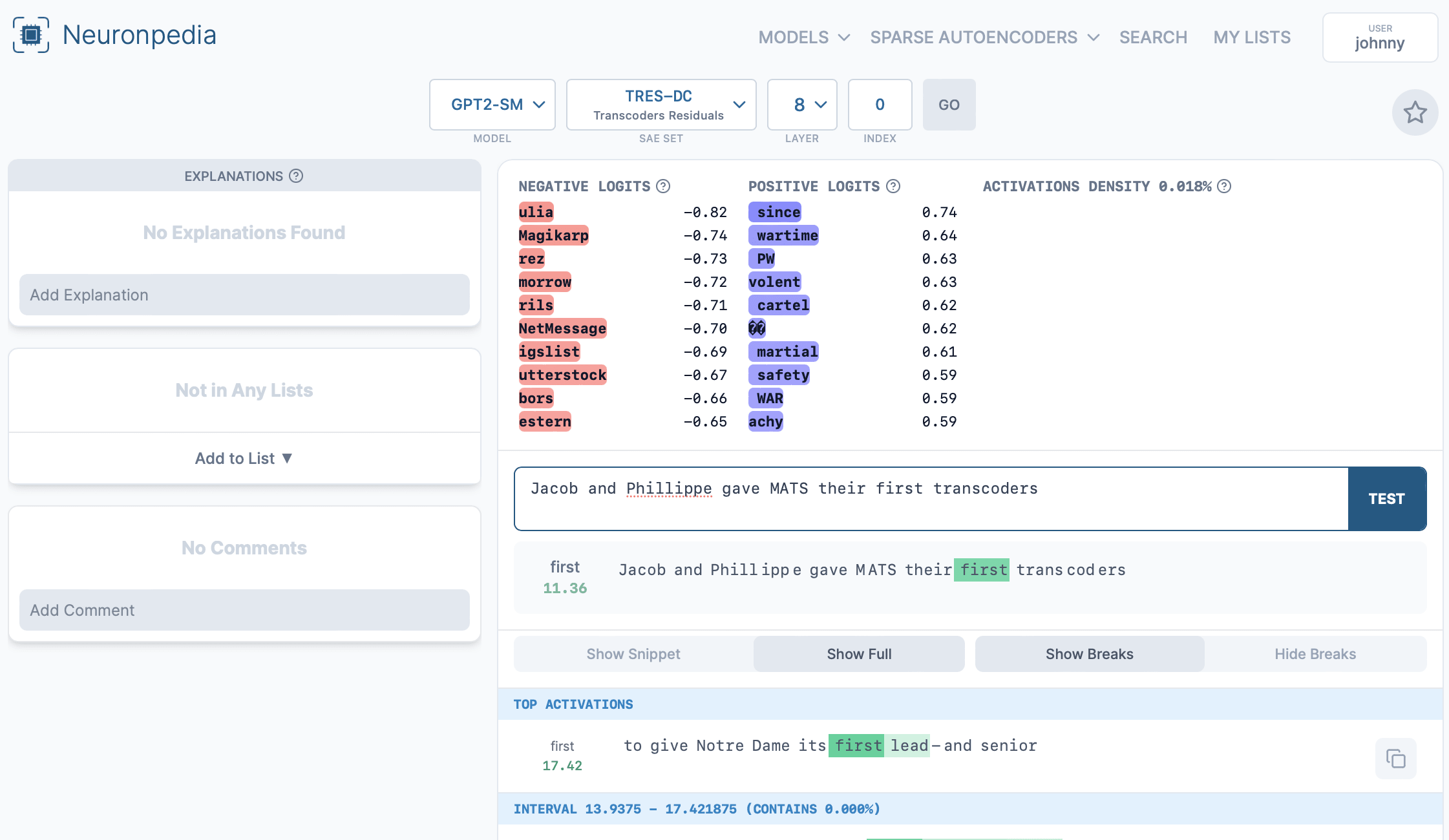
Or search all features at: https://www.neuronpedia.org/gpt2-small/tres-dc
An example search: https://www.neuronpedia.org/gpt2-small/?sourceSet=tres-dc&selectedLayers=[]&sortIndexes=[]&q=the%20cat%20sat%20on%20the%20mat%20at%20MATS
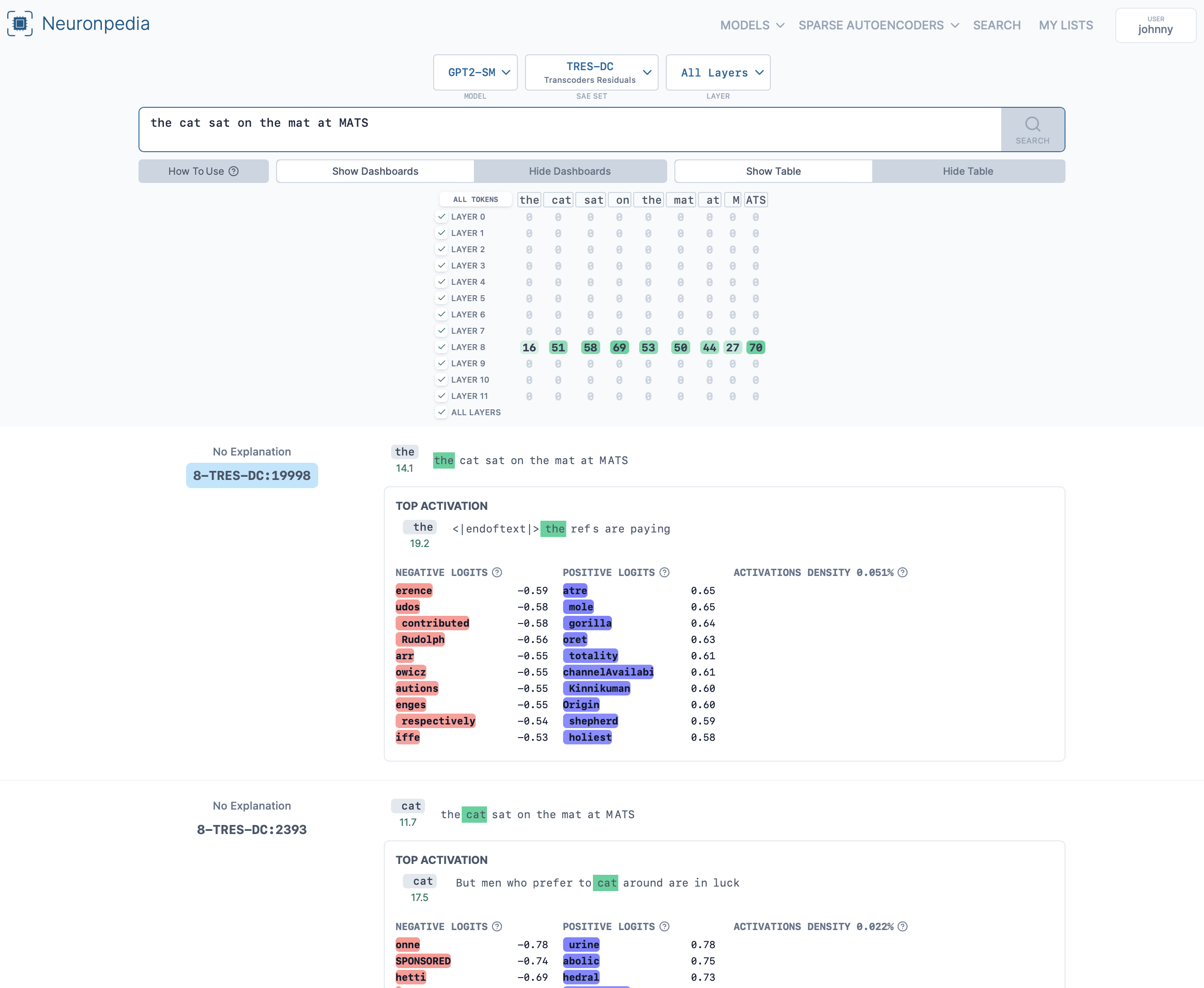
Unfortunately I wasn't able to generate histograms, autointerp, or other layers for this yet. Am working on getting more layers up first.
Verification
I did spot checks of the first few dashboards and they seem to be correct. Please let me know if anything seems wrong or off. I am also happy to delete this comment if you do not find it useful or for any other reason - no worries.
Please let me know if you have any feedback or issues with this. I will be also reaching out directly via Slack.
Nice! We were originally planning to train sparse MLPs like this this week.
Do you have any plans of doing something similar for attention layers? Replacing them with wider attention layers with a sparsity penalty, on the hypothesis that they'd then become more monosemantic?
Also, do you have any plans to train sparse MLP at multiple layers in parallel, and try to penalise them to have sparsely activating connections between each other in addition to having sparse activations?
Do you have any plans of doing something similar for attention layers?
I'm pretty sure that there's at least one other MATS group (unrelated to us) currently working on this, although I'm not certain about any of the details. Hopefully they release their research soon!
Also, do you have any plans to train sparse MLP at multiple layers in parallel, and try to penalise them to have sparsely activating connections between each other in addition to having sparse activations?
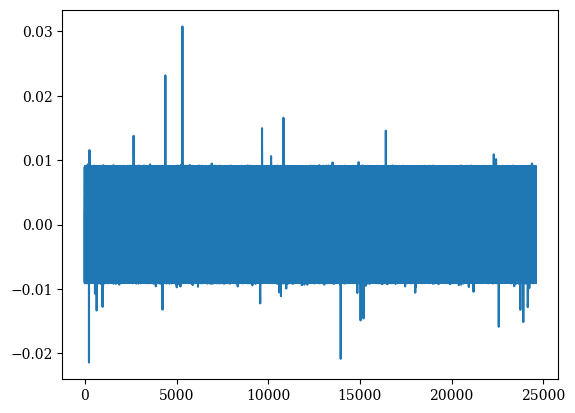
I did try something similar at one point, but it didn't quite work out. In particular: given an SAE for MLP-out activations, you can try and train an MLP transcoder with an additional loss term penalizing the L1 norm of the pullback of the SAE encoder features by the transcoder decoder matrix. This was intended to induce sparse input-independent connections from the transcoder features to the MLP-out SAE features. Unfortunately, this didn't yield great results. The transcoder features were often polysemantic, while the input-independent connections from the transcoder features to the SAE features were somewhat bizarre-looking. Here's an old graph I just dug up: the x-axis is transcoder feature index and the y-axis is the input-independent connection strength to a certain SAE feature:
In the end, I decided to pause working on this idea. Potentially, it could turn out that this idea is workable, but if so, then there are probably a few extra tweaks that have to be done to get it working beyond the naive approach that I tried.
I'm pretty sure that there's at least one other MATS group (unrelated to us) currently working on this, although I'm not certain about any of the details. Hopefully they release their research soon!
There's recent work published on this here by Chris Mathwin, Dennis Akar, and me. The gated attention block is a kind of transcoder adapted for attention blocks.
Nice work by the way! I think this is a promising direction.
Note also the similar, but substantially different, use of the term transcoder here, whose problems were pointed out to me by Lucius. Addressing those problems helped to motivate our interest in the kind of transcoders that you've trained in your work!
they [transcoders] take as input the pre-MLP activations, and then aim to represent the post-MLP activations of that MLP sublayer
I assumed this meant activations just before GELU and just after GELU, but looking at code I think I was wrong. Could you rephrase to e.g.
they take as input MLP block inputs (just after LayerNorm) and they output MLP block outputs (what is added to the residual stream)
There is a tradeoff between interpretability and fidelity
I wonder what would happen if something like transcoders is used to guide pre-training in a way similar to quantization-aware training. There, forward passes are computed under quantization, while gradients and optimizer states are maintained in full precision. For extreme levels of quantization, this produces quantized models that achieve loss much closer to that of a full-precision model, compared to post-training quantization (to the same degree) of a model whose training wasn't guided this way. With transcoders, "full precision" is the MLPs, while "quantization" is transition to the corresponding transcoders.
This sounds like it could work. I can think of a few reasons why this approach could be challenging, however:
1. We don't really know how transcoders (or SAEs, to the best of my knowledge) behave when they're being trained to imitate a model component that's still updating
2. Substituting multiple transcoders at once is possible, but degrades model performance a lot compared to single-transcoder substitutions. Substituting one transcoder at a time would require restarting the forward pass at each layer.
3. If the transcoders are used to predict next tokens, they may lose interpretability and return to superposition.
Under a "transcoder-aware" training regime, these would be the first things I would check for.
Also, you may be interested in Jacob's comment here for some details on when we tried to co-train SAEs and transcoders to have sparse connections to one another. This is a very different question, of course, but it provides some preliminary evidence that the fidelity-interpretability tradeoff persists across more elaborate training settings.
If the transcoders are used to predict next tokens, they may lose interpretability
Possibly. But there is no optimization pressure from pre-training on the relationship between MLPs and transcoders. The MLPs are the thing that pre-training optimizes (as the "full-precision" master model), while transcoders only need to be maintained to remain in sync with the MLPs, whatever they are (according to the same local objective as before, which doesn't care at all about token prediction). The search is for MLPs such that their transcoders are good predictors, not directly for transcoders that are good predictors.
Substituting multiple transcoders at once is possible, but degrades model performance a lot compared to single-transcoder substitutions.
Unclear given the extreme quantization results, where similarly post-training replacement would degrade model performance a lot, yet quantization-aware pre-training somehow doesn't.
We don't really know how transcoders (or SAEs, to the best of my knowledge) behave when they're being trained to imitate a model component that's still updating
This seems to be the main technical hurdle to do the experiment, updating transcoders both efficiently and correctly, as underlying MLPs gradually change. (I'm guessing some discontinuous jumps in choice of transcoders might be OK.)
Possibly. But there is no optimization pressure from pre-training on the relationship between MLPs and transcoders. The MLPs are the thing that pre-training optimizes (as the "full-precision" master model), while transcoders only need to be maintained to remain in sync with the MLPs
I see. I was in fact misunderstanding this detail in your training setup. In this case, only engineering considerations really remain: these boil down to incorporating multiple transcoders simultaneously and modeling shifting MLP behavior with transcoders. These seem like tractable, although probably nontrivial and, because of the LLM pretraining objective, quite computationally expensive. If transcoders catch on, I hope to see someone with the compute budget for it run this experiment!
Hey Jacob + Philippe,
I took the liberty of making a clean installable version of your original codebase. Hope you don't mind, and happy to make any changes that you request! https://github.com/dtch1997/transcoders-slim
Question about the "rules of the game" you present. Are you allowed to simply look at layer 0 transcoder features for the final 10 tokens - you could probably roughly estimate the input string from these features' top activators. From you case study, it seems that you effectively look at layer 0 transcoder features for a few of the final tokens through a backwards search, but wonder if you can skip the search and simply look at transcoder features. Thank you.
Summary
Work performed as a part of Neel Nanda's MATS 5.0 (Winter 2024) stream and MATS 5.1 extension. Jacob Dunefsky is currently receiving funding from the Long-Term Future Fund for this work.
Background and motivation
Mechanistic interpretability is fundamentally concerned with reverse-engineering models’ computations into human-understandable parts. Much early mechanistic interpretability work (e.g. indirect object identification) has dealt with decomposing model computations into circuits involving small numbers of model components like attention heads or MLP sublayers.
But these component-level circuits operate at too coarse a granularity: due to the relatively small number of components in a model, each individual component will inevitably be important to all sorts of computations, oftentimes playing different roles. In other words, components are polysemantic. Therefore, if we want a more faithful and more detailed understanding of the model, we should aim to find fine-grained circuits that decompose the model’s computation onto the level of individual feature vectors.
As a hypothetical example of the utility that feature-level circuits might provide in the very near-term: if we have a feature vector that seems to induce gender bias in the model, then understanding which circuits this feature vector partakes in (including which earlier-layer features cause it to activate and which later-layer features it activates) would better allow us to understand the side-effects of debiasing methods. More ambitiously, we hope that similar reasoning might apply to a feature that would seem to mediate deception in a future unaligned AI: a fuller understanding of feature-level circuits could help us understand whether this deception feature actually is responsible for the entirety of deception in a model, or help us understand the extent to which alignment methods remove the harmful behavior.
Some of the earliest work on SAEs aimed to use them to find such feature-level circuits (e.g. Cunningham et al. 2023). But unfortunately, SAEs don’t play nice with circuit discovery methods. Although SAEs are intended to decompose an activation into an interpretable set of features, they don’t tell us how this activation is computed in the first place.[1]
Now, techniques such as path patching or integrated gradients can be used to understand the effect that an earlier feature has on a later feature (Conmy et al. 2023; Marks et al. 2024) for a given input. While this is certainly useful, it doesn’t quite provide a mathematical description of the mechanisms underpinning circuits[2], and is inherently dependent on the inputs used to analyze the model. If we want an interpretable mechanistic understanding, then something beyond SAEs is necessary.
Solution: transcoders
To address this, we utilize a tool that we call transcoders[3]. Essentially, transcoders aim to learn a "sparsified" approximation of an MLP sublayer. SAEs attempt to represent activations as a sparse linear combination of feature vectors; importantly, they only operate on activations at a single point in the model. In contrast, transcoders operate on activations both before and after an MLP sublayer: they take as input the pre-MLP activations, and then aim to represent the post-MLP activations of that MLP sublayer as a sparse linear combination of feature vectors. In other words, transcoders learn to map MLP inputs to MLP outputs through the same kind of sparse, overparamaterized latent space used by SAEs to represent MLP activations.[4]
The idea of transcoders has been discussed by Sam Marks and by Adly Templeton et al. Our contributions are to construct a family of transcoders on GPT-2 small, to provide a detailed analysis of the quality of transcoders (compared to SAEs) and their utility for circuit analysis, and to open source transcoders and code for using them.
Code can be found at https://github.com/jacobdunefsky/transcoder_circuits, and a set of trained transcoders for GPT2-small can be found at https://huggingface.co/pchlenski/gpt2-transcoders.
In the next two sections, we provide some evidence that transcoders display comparable performance to SAEs in both quantitative and qualitative metrics. Readers who are more interested in transcoders’ unique strengths beyond those of SAEs are encouraged to skip to the section “Circuit Analysis.”
Performance metrics
We begin by evaluating transcoders’ performance relative to SAEs. The standard metrics for evaluating performance (as seen e.g. here and here) are the following:
There is a tradeoff between interpretability and fidelity: more-interpretable models are usually less faithful, and vice versa. This tradeoff is largely mediated by the hyperparameter λ1, which determines the importance of the sparsity penalty term in the SAE/transcoder loss. Thus, by training SAEs/transcoders with different λ1 values, we can visualize the Pareto frontier governing this tradeoff. If transcoders achieve a similar Pareto frontier to SAEs, then this might suggest their viability as a replacement for SAEs.
We trained eight different SAEs and transcoders on layer 8 of GPT2-small, varying the values of λ1 used to train them. (All SAEs and transcoders were trained at learning rate 4⋅10−4. Layer 8 was chosen largely heuristically – we figured that it’s late enough in the model that the features learned should be somewhat abstract and interesting, without being so late in the model that the features primarily correspond to “next-token-prediction” features.) The resulting Pareto frontiers are shown in the below graph:
Importantly, it appears that the Pareto frontier for the loss-sparsity tradeoff is approximately the same for both SAEs and transcoders (in fact, transcoders seemed to do slightly better). This suggests that no additional cost is incurred by using transcoders over SAEs. But as we will see later, transcoders yield significant benefits over SAEs in circuit analysis. These results therefore suggest that going down the route of using transcoders instead of SAEs is eminently reasonable.
So far, our qualitative evaluation has addressed transcoders at individual layers in the model. But later on, we will want to simultaneously use transcoders at many different layers of the model. To evaluate the efficacy of transcoders in this setting, we took a set of transcoders that we trained on all layers of GPT2-small, and replaced all the MLP layers in the model with these transcoders. We then looked at the mean cross-entropy loss of the transcoder-replaced model, and found it to be 4.23 nats. When the layer 0 and layer 11 MLPs are left intact[6], this drops down to 4.06 nats. For reference, recall that the original model’s cross-entropy loss (on the subset of OpenWebText that we used) was 3.59 nats. These results further suggest that transcoders achieve decent fidelity to the original model, even when all layers’ MLPs are simultaneously replaced with transcoders.
Qualitative interpretability analysis
Example transcoder features
For a more qualitative perspective, here are a few cherry-picked examples of neat features that we found from the Layer 8 GPT2-small transcoder with λ1=8⋅10−5:
Broader interpretability survey
In order to get a further sense of how interpretable transcoder features are, we took the first 30 live features[7] in this Layer 8 transcoder, looked at the dataset examples that cause them to fire the most, and attempted to find patterns in these top-activating examples.
We found that only one among the 30 features didn’t display an interpretable pattern[8].
Among the remaining features, 5 were features that always seemed to fire on a single token, without any further interpretable patterns governing the context of when the feature fires.[9] An additional 4 features fired on different forms of a single verb (e.g. fired on “fight”, “fights”, “fought”).
This meant that the remaining 20/30 features had complex, interpretable patterns. This further strengthened our optimism towards transcoders, although more rigorous analysis is of course necessary.
Circuit analysis
So far, our results have suggested that transcoders are equal to SAEs in both interpretability and fidelity. But now, we will investigate a feature that transcoders have that SAEs lack: we will see how they can be used to perform fine-grained circuit analysis that yields generalizing results, in a specific way that we will soon formally define.
Fundamentally, when we approach circuit analysis with transcoders, we are asking ourselves which earlier-layer transcoder features are most important for causing a later-layer feature to activate. There are two ways to answer this question. The first way is to look at input-independent information: information that tells us about the general behavior of the model across all inputs. The second way is to look at input-dependent information: information that tells us about which features are important on a given input.
Input-independent information: pullbacks and de-embeddings
The input-independent importance of an earlier-layer feature to a later-layer feature gives us a sense of the conditional effect that the earlier-layer feature firing has on the later-layer feature. It answers the following question: if the earlier-layer feature activates by a unit amount, then how much does this cause the later-layer feature to activate? Because this is conditional on the earlier-layer feature activating, it is not dependent on the specific activation of that feature on any given input.
This input-independent information can be obtained by taking the "pullback" of the later-layer feature vector by the earlier-layer transcoder decoder matrix. This can be computed as p=(Wdec)Tflater: multiply the later-layer feature vector flater by the transpose of the earlier-layer transcoder decoder matrix Wdec. Component i of the pullback p tells us that if earlier-layer feature i has activation k, then this will cause the later-layer feature’s activation to increase by kpi.[10]
Here’s an example pullback that came up in one of our case studies:
This shows how much each feature in a transcoder for layer 0 in GPT2-small will cause a certain layer 6 transcoder feature to activate. Notice how there are a few layer 0 features (such as feature 16382 and feature 5468) that have outsized influence on the layer 6 feature. In general, though, there are many layer 0 features that could affect the layer 6 feature.
A special case of this “pullback” operation is the operation of taking a de-embedding of a feature vector. The de-embedding of a feature vector is the pullback of the feature vector by the model’s vocabulary embedding matrix. Importantly, the de-embedding tells us which tokens in the model’s vocabulary most cause the feature to activate.
Here is an example de-embedding for a certain layer 0 transcoder feature:
For this feature, the tokens in the model’s vocabulary that cause the feature to activate the most seem to be tokens from surnames – Polish surnames in particular.
Input-dependent information
There might be a large number of earlier-layer features that could cause a later-layer feature to activate. However, transcoder sparsity ensures only a small number of earlier-layer features will be active at any given time on any given input. Thus, only a small number will be responsible for the later-layer feature to activate.
The input-dependent influence q of features in an earlier-layer transcoder upon a later-layer feature vector f is given as follows: q=z(x)⊙p, where ⊙ denotes component-wise multiplication of vectors, z(x) is the vector of earlier-layer transcoder feature activations on input x, and p is the pullback of f with respect to the earlier-layer transcoder. Component i of the vector q thus tells you how much earlier-layer feature i contributes to feature f’s activation on the specific input x.
As an example, here’s a visualization of the input-dependent connections on a certain input for the same layer 6 transcoder feature whose pullback we previously visualized:
This means that on this specific input, layer 0 transcoder features 23899, 16267, and 4328 are most important for causing the layer 6 feature to activate. Notice how, in comparison to the input-independent feature connections, the input-dependent connections are far sparser.
Importantly, this approach cleanly factorizes feature attribution into two parts: an input-independent part (the pullback) multiplied elementwise with an input-dependent part (the transcoder feature activations). Since both parts and their combination are individually interpretable, the entire feature attribution process is interpretable. This is what we formally mean when we say that transcoders make MLP computation interpretable in a generalizing way.
Obtaining circuits and graphs
We can use the above techniques to determine which earlier-layer transcoder features are important for causing a later-layer transcoder feature to activate. But then, once we have identified some earlier-layer feature i that we care about, then we can understand what causes feature i to activate by repeating this process, looking at the encoder vector for feature i in turn and seeing which earlier-layer features cause it to activate.
By iteratively applying these methods in this way, we can automatically construct a sparse computational graph that decomposes the model's computation on a given input into transcoder features at various layers and the connections between them. This is done via a greedy search algorithm, which is described in more detail in the appendix.
Brief discussion: why are transcoders better for circuit analysis?
As mentioned earlier, SAEs are primarily a tool for analyzing activations produced at various stages of a computation rather than the computation itself: you can use SAEs to understand what information is contained in the output of an MLP sublayer, but it’s much harder to use them to understand the mechanism by which this output is computed. Now, attribution techniques like path patching or integrated gradients can provide approximate answers to the question of which pre-MLP SAE features are most important for causing a certain post-MLP SAE feature to activate on a given input. But this local information doesn’t quite explain why those pre-MLP features are important, or how they are processed in order to yield the post-MLP output.
In contrast, a faithful transcoder makes the computation itself implemented by an MLP sublayer interpretable. After all, a transcoder emulates the computation of an MLP by calculating feature activations and then using them as the coefficients in a weighted sum of decoder vectors. These feature activations are both computationally simple (they’re calculated by taking dot products with encoder vectors, adding bias terms, and then taking a ReLU) and interpretable (as we saw earlier when we qualitatively assessed various features in our transcoder). This means that if we have a faithful transcoder for an MLP sublayer, then we can understand the computation of the MLP by simply looking at the interpretable feature activations of the transcoder.
As an analogy, let’s say that we have some complex compiled computer program that we want to understand (a la Chris Olah’s analogy). SAEs are analogous to a debugger that lets us set breakpoints at various locations in the program and read out variables. On the other hand, transcoders are analogous to a tool for replacing specific subroutines in this program with human-interpretable approximations.
Case study
In order to evaluate the utility of transcoders in performing circuit analysis, we performed a number of case studies, where we took a transcoder feature in Layer 8 in the model, and attempted to reverse-engineer it – that is, figure out mechanistically what causes it to activate. For the sake of brevity, we’ll only be presenting one of these case studies in this post, but you can find the code for the others at https://github.com/jacobdunefsky/transcoder_circuits.
Introduction to blind case studies
The following case study is what we call a “blind case study.” The idea is this: we have some feature in some transcoder, and we want to interpret this transcoder feature without looking at the examples that cause it to activate. Our goal is to instead come to a hypothesis for when the feature activates by solely using the input-independent and input-dependent circuit analysis methods described above.
The reason why we do blind case studies is that we want to evaluate how well our circuit analysis methods can help us understand circuits beyond the current approach of looking for patterns in top activating examples for features. After all, we want to potentially be able to apply these methods to understanding complex circuits in state-of-the-art models where current approaches might fail. Furthermore, looking at top activating examples can cause confirmation bias in the reverse-engineering process that might lead us to overestimate the effectiveness and interpretability of the transcoder-based methods.
To avoid this, we have the following “rules of the game” for performing blind case studies:
Blind case study on layer 8 transcoder feature 355
For our case study, we decided to reverse-engineer feature 355 in our layer 8 transcoder on GPT2-small[11]. This section provides a slightly-abridged account of the paths that we took in this case study; readers interested in all the details are encouraged to refer to the notebook
case_study_citations.ipynb.We began by getting a list of indices of the top-activating inputs in the dataset for feature 355. Importantly, we did not look at the actual tokens in these inputs, as doing so would violate the “blind case study” self-imposed constraint. The first input that we looked at was example 5701, token 37; the transcoder feature fires at strength 11.91 on this token in this input. Once we had this input, we ran our greedy algorithm to get the most important computational paths for causing this feature to fire. Doing so revealed contributions from the current token (token 37) as well as contributions from earlier tokens (like 35, 36, and 31).
First, we looked at the contributions from the current token. There were strong contributions from this token through layer 0 transcoder features 16632 and 9188. We looked at the input-independent de-embeddings of these layer 0 features, and found that these features primarily activate on semicolons. This indicates that the current token 37 contributes to the feature by virtue of being a semicolon.
Similarly, we saw that layer 6 transcoder feature 11831 contributes strongly. We looked at the input-independent connections from layer 0 transcoder features to this layer 6 feature, in order to see which layer 0 features cause the layer 6 feature to activate the most in general. Sure enough, the top features were 16632 and 9188 – the layer 0 semicolon features that we just saw.
The next step was to investigate computational paths that come from previous tokens in order to understand what in the context caused the layer 8 feature to activate. Looking at these contextual computational paths revealed that token 36 contributes to the layer 8 feature firing through layer 0 feature 13196, whose top de-embeddings are years like 1973, 1971, 1967, and 1966. Additionally, token 31 contributes to the layer 8 feature firing through layer 0 feature 10109, whose top de-embedding is an open parenthesis token.
Furthermore, the layer 6 feature 21046 was found to contribute at token 35. The top input-independent connections to this feature from layer 0 were the features 16382 and 5468. In turn, the top de-embeddings for the former feature were tokens associated with Polish last names (e.g. “kowski”, “chenko”, “owicz”) and the top de-embeddings for the latter feature were English surnames (e.g. “Burnett”, “Hawkins”, “Johnston”, “Brewer”, “Robertson”). This heavily suggested that layer 6 feature 21046 is a feature that fires upon surnames.
At this point, we had the following information:
Putting this together, we formulated the following hypothesis: the layer 8 feature fires whenever it sees semicolons in parenthetical academic citations (e.g. the semicolon in a citation like “(Vaswani et al. 2017; Elhage et al. 2021)”.
We performed further investigation on another input and found a similar pattern (e.g. layer 6 feature 11831, which fired on a semicolon in the previous input; an open parenthesis feature; a year feature). Interestingly, we also found a slight contextual contribution from layer 0 feature 4205, whose de-embeddings include tokens like “Accessed”, “Retrieved”, “ournals” (presumably from “Journals”), “Neuroscience”, and “Springer” (a large academic publisher) – which further reinforces the academic context, supporting our hypothesis.
Evaluating our hypothesis
At this point, we decided to end the “blind” part of our blind case study and look at the feature’s top activating examples in order to evaluate how we did. Here are the results:
Yep – it turns out that the top examples are from semicolons in academic parenthetical citations! Interestingly, it seems that lower-activating examples also fire on semicolons in general parenthetical phrases. Perhaps a further investigation on lower-activating example inputs would have revealed this.
Code
As a part of this work, we’ve written quite a bit of code for training, evaluating, and performing circuit analysis with transcoders. A repository containing this code can be found at https://github.com/jacobdunefsky/transcoder_circuits/, and contains the following items:
transcoder_training/, a fork of Joseph Bloom’s SAE training library with support for transcoders. In the main directory,train_transcoder.pyprovides an example script that can be adapted to train your own transcoders.transcoder_circuits/, a Python package that allows for the analysis of circuits using transcoders.transcoder_circuits.circuit_analysiscontains code for analyzing circuits, computational paths, and graphs.transcoder_circuits.feature_dashboardscontains code for producing “feature dashboards” for individual transcoder features within a Jupyter Notebook.transcoder_circuits.replacement_ctxprovides a context manager that automatically replaces MLP sublayers in a model with transcoders, which can then be used to evaluate transcoder performance.walkthrough.ipynb: a Jupyter Notebook providing an overview of how to use the various features of transcoder_circuits.case_study_citation.ipynb: a notebook providing the code underpinning the blind case study of an “academic parenthetical citation” feature presented in this post.case_study_caught.ipynb: a notebook providing the code underpinning a blind case study of a largely-single-token “caught” transcoder feature, not shown in this post. There is also a discussion of a situation where the greedy computational path algorithm fails to capture the full behavior of the model’s computation.case_study_local_context.ipynb: a notebook providing the code underpinning a blind case study of a “local-context” transcoder feature that fires on economic statistics, not shown in this post. In this blind case study, we failed to correctly hypothesize the behavior of the feature before looking at maximum activating examples, but we include it among our code in the interest of transparency.Discussion
A key goal of SAEs is to find sparse, interpretable linear reconstructions of activations. We have shown that transcoders are comparable to SAEs in this regard: the Pareto frontier governing the tradeoff between fidelity and sparsity is extremely close to that of SAEs, and qualitative analyses of their features suggest comparable interpretability to SAEs. This is pleasantly surprising: even though transcoders compute feature coefficients from MLP inputs, they can still find sparse, interpretable reconstructions of the MLP output.
We think that transcoders are superior to SAEs because they enable circuit analysis through MLP nonlinearities despite superposition in MLP layers. In particular, transcoders decompose MLPs into a sparse set of computational units, where each computational unit consists of taking the dot product with an encoder vector, applying a bias and a ReLU, and then scaling a decoder vector by this amount. Each of these computations composes well with the rest of the circuit, and the features involved tend to be as interpretable as SAE features.
As for the limitations of transcoders, we like to classify them in three ways: (1) problems with transcoders that SAEs don’t have, (2) problems with SAEs that transcoders inherit, and (3) problems with circuit analysis that transcoders inherit:
At this point, we are very optimistic regarding the utility of transcoders. As such, we plan to continue investigating them, by pursuing directions including the following:
Of course, we also plan to perform more evaluations and analyses of the transcoders that we currently have. In the meantime, we encourage you to play around with the transcoders and circuit analysis code that we’ve released. Thank you for reading!
Author contribution statement
Jacob Dunefsky and Philippe Chlenski are both core contributors. Jacob worked out the math behind the circuit analysis methods, wrote the code, and carried out the case studies and experiments. Philippe trained the twelve GPT2-small transcoders, carried out hyperparameter sweeps, and participated in discussions on the circuit analysis methods. Neel supervised the project and came up with the initial idea to apply transcoders to reverse-engineer features.
Acknowledgements
We are grateful to Josh Batson, Tom Henighan, Arthur Conmy, and Tom Lieberum for helpful discussions. We are also grateful to Joseph Bloom for writing the wonderful SAE training library upon which we built our transcoder training code.
Appendix
For input-dependent feature connections, why pointwise-multiply the feature activation vector with the pullback vector?
Here's why this is the correct thing to do. Ignoring error in the transcoder's approximation of the MLP layer, the output of the earlier-layer MLP layer can be written as a sparse linear combination of transcoder features c1f1+...+ckfk, where the ci are the feature activation coefficients and the feature vectors fi are the columns of the transcoder decoder matrix Wdec. If the later-layer feature vector is flater, then the contribution of the earlier MLP to the activation of flater is given by c1fT1flater+...+ckfTkflater. Thus, the contribution of feature i is given by cifTiflater. But then this is just the i-th entry in the vector c⊙((Wdec)Tflater), which is the pointwise product of the pullback with the feature activations.
Note that the pullback is equivalent to the gradient of the later-layer feature vector with respect to the earlier-layer transcoder feature activations. Thus, the process of finding input-dependent feature connections is a case of the “input-times-gradient” method of calculating attributions that’s seen ample use in computer vision and early interpretability work. The difference is that now, we’re applying it to features rather than pixels.
Comparing input-independent pullbacks with mean input-dependent attributions
Input-independent pullbacks are an inexpensive way to understand the general behavior of connections between transcoder features in different layers. But how well do pullbacks predict the features with the highest input-dependent connections?
To investigate this, we performed the following experiment. We are given a later-layer transcoder feature and an earlier-layer transcoder. We can use the pullback to obtain a ranking of the most important earlier-layer features for the later-layer feature. Then, on a dataset of inputs, we calculate the mean input-dependent attribution of each earlier-layer feature for the later-layer feature over the dataset. We then look at the top k features according to pullbacks and according to mean input-dependent attributions, for different values of k. Then, to measure the degree of agreement between pullbacks and mean input-dependent attributions, for each value of k, we look at the proportion of features that are in both the set of top k pullback features and the set of top k mean input-dependent features.
We performed this experiment using two different
(earlier_layer_transcoder, later_layer_feature)pairs, both of which pairs naturally came up in the course of our investigations.First, we looked at the connections from MLP0 transcoder features to MLP5 transcoder feature 12450.
The following graph shows the results for 1≤k≤100:
Then, we looked at the connections from MLP2 transcoder features to MLP8 transcoder feature 89.
The following graph shows the results for 1≤k≤100:
A more detailed description of the computational graph algorithm
At the end of the section on circuit analysis, we mention that these circuit analysis techniques can be used in an algorithm for constructing a sparse computational graph containing the transcoder features and connections between them with the greatest importance to a later-layer transcoder feature on a given input. The following is a description of this algorithm:
Note that the above description does not take into account attention heads. Attention heads are dealt with in the full algorithm as follows. Following the standard workaround, QK scores are treated as fixed constants. Then, the importance of an attention head for causing a feature vector to activate is computed by taking the dot product of the feature vector with the attention head’s output and weighting it by the attention score of the QK circuit (as is done in our previous work). The attention head is then associated with a feature vector of its own, which is given by the pullback of the later-layer feature by the OV matrix of the attention head.
The full algorithm also takes into account pre-MLP and pre-attention LayerNorms by treating them as constants by which the feature vectors are scaled, following the approach laid out in Neel Nanda’s blogpost on attribution patching).
Readers interested in the full details of the algorithm are encouraged to look at the code contained in
transcoder_circuits/circuit_analysis.py.Details on evaluating transcoders
In our evaluation of transcoders, we used 1,638,400 tokens taken from the OpenWebText dataset, which aims to replicate the proprietary training dataset used to train GPT2-small. These tokens were divided into prompts of 128 tokens each; our transcoders (and the SAEs that we compared them against) were also trained on 128-token-long prompts. Previous evaluations of SAEs suggest that evaluating these transcoders on longer prompts than those on which they were trained will likely yield worse results.
In particular, if we want a method to understand how activations are computed, then it needs to account for MLP sublayers. SAEs could potentially help by disentangling these activations into sparse linear combinations of feature vectors. We thus might hope that the mappings between pre-MLP feature vectors and post-MLP features are likewise sparse, as this would give us a compact description of MLP computations. But SAE feature vectors are dense in the standard MLP basis; there are very few components close to zero. In situations such as dealing with OV circuits, this sort of basis-dependent density doesn’t matter, because you can just use standard linear algebra tools like taking dot products to obtain useful interpretations. But this isn’t possible with MLPs, because MLPs involve component-wise nonlinearities (e.g. GELU). Thus, looking at connections between SAE features means dealing with thousands of simultaneous, hard-to-interpret nonlinearities. As such, using SAEs alone won’t help us find a sparse mapping between pre-MLP and post-MLP features, so they don’t provide us with any more insight into MLP computations.
When we refer to a “mathematical description of the mechanisms underpinning circuits,” we essentially mean a representation of the circuit in terms of a small number of linear-algebraic operations.
Note that Sam Marks calls transcoders “input-output SAEs,” and the Anthropic team calls them “predicting future activations.” We use the term "transcoders," which we heard through the MATS grapevine, with ultimate provenance unknown.
In math: an SAE has the architecture (ignoring bias terms) SAE(x)=WoutReLU(Winx), and is trained with the loss∥SAE(x)−x∥2+λ1∥ReLU(Winx)∥1, where λ1 is a hyperparameter and ∥⋅∥1 denotes the ℓ1 norm. In contrast, although a transcoder has the same architecture TC(x)=WoutReLU(Winx), it is trained with the loss ∥TC(x)−MLP(x)∥2+λ1∥ReLU(Winx)∥1, meaning that we look at the mean squared error between the transcoder’s output and the MLP’s output, rather than the transcoder’s output and its own input.
Note that the mean ablation baseline doesn’t yield that much worse loss than the original unablated model. We hypothesize that this is due to the fact that GPT2-small was trained with dropout, meaning that “backup” circuits within the model can cause it to perform well even if an MLP sublayer is ablated.
Empirically, we found that the layer 0 transcoder and layer 11 transcoder displayed higher MSE losses than the other layers’ transcoders. The layer 0 case might be due to the hypothesis that GPT2-small uses layer 0 MLPs as “extended token embeddings”. The layer 11 case might be caused by similar behavior on the unembedding side of things, but in this case, hypotheses non fingimus.
A live feature is a feature that activates more frequently than once every ten thousand tokens.
For reference, here is the feature dashboard for the lone uninterpretable feature:

If you can make any sense of this pattern, then props to you.
In contrast, here are some examples of single-token features with deeper contextual patterns. One such example is the word "general" as an adjective (e.g. the feature fires on “Last season, she was the general manager of the team” but not “He was a five-star general”). Another example is the word "with" after verbs/adjectives that regularly take "with" as a complement (e.g. the feature fires on “filled with joy” and “buzzing with activity”, but not “I ate with him yesterday”).
The reason that the pullback has this property is that, as one can verify, the pullback is just the gradient of the later-layer feature activation with respect to the earlier-layer transcoder feature activations.
As mentioned earlier, we chose to look at layer 8 because we figured that it would contain some interesting, relatively-abstract features. We chose to look at feature 355 because this was the 300th live feature in our transcoder (and we had already looked at the 100th and 200th live features in non-blind case studies).