[Epistemic status: I have running code that implements it.]

Overview: I previously showed how an FFN layer in a transformer can be implemented via 3 attention layers. In this post I show how to do it in a single attention layer. This reduces the needed dimensionality of your model from 5D+N+1 to D+N+1. The main bottleneck, needing 4D attention heads for the hidden layers, remains.

Hot Take: [epistemic status: much less confidence than the rest of this post] The bottleneck - that one needs 4D attention heads for the hidden layers - could be capturing a mechanistic interpretability insight: the FFN components of transformers are less interpretable simply because they consist of ~500x more attention heads than a traditional attention layer. This could suggest a “scale is all you need” approach to mechanistic interpretability - we’ll be able to understand large attention-only models if and only if we can understand smaller FFN+attention models.

Outline: I’ll cover two perspectives that helped me realize you could do this simplification, then summarize the changes, link to the code, then give some concluding thoughts.

I will assume you are familiar with the previous post and it’s notation, so if read it here if you need a refresher.

Perspective 1 - Identical Steps

I first realized we could simplify this by imagining the perspective of a single entry in the hidden layer of a transformer’s FFN. We:

• (F1) Compute the entry via linear operation on the residual stream
• (F2) Apply a nonlinearity (the activation function)
• (F3) Write to the residual stream via a linear operation

Compare with the steps in an attention head:

• (A1) Compute pre-attention via a linear operation on the residual stream
• (A2) Apply a nonlinearity (the rowwise softmax)
• (A3) Write to the residual stream via a linear operation

Suspiciously similar! In my previous post, I used separate attention layers for F1, F2, and F3, but one can actually choose Q and V matrices so that A1/2/3 computes F1/2/3, respectively, allowing you to complete the FFN in a single attention layer.

Perspective 2 - Virtual Attention Heads

A Mathematical Framework for Transformer Circuits introduced “virtual attention heads”, which provide another useful intuition.

In short, attention heads in two consecutive layers can (in some sense) be treated as a single combined “virtual” attention head. Writing $A_i$ for the attention patters and $V_i$ for the weights being written to the residual stream, attention heads are characterized by $A_i\otimes V_i$, and the virtual attention head produced by $A_1\otimes V_1$ and $A_2\otimes V_2$ is $\left(A_1{A}_2\right)\otimes \left(V_1{V}_2\right)$, with the caveat that the attention pattern from layer 1 influences the attention pattern in layer 2.

Since this part is just to build intuition, we’re going to play fast and loose with notation and matrix sizes. But applying this analysis to the linear, SiLU, and linear sublayers described in the previous post, we get:

• $A_1\otimes V_1$: For the first linear layer, we forced every vector to only attend to itself, so we have $A_1$$=I$ (the identity matrix). Our $V_1$ matrix contained a copy of the weight matrix $W_1$, so in an abuse of notation let us write $V_1=W_1$.
• $A_2\otimes V_2$: For the SiLU layer, our $A_2$ matrix is complicated. But our $V_2$ matrix is a matrix unit $-E_k=-E_{k,k}$, where $k$ is the dimension being SiLU’d.
• $A_3\otimes V_3$: For the second linear layer, we forced every vector to only attend to itself, so we have $A_3=I$ (the identity matrix). Our $V_3$ matrix contained a copy of the weight matrix $W_2$, so in an abuse of notation let us write $V_3=W_2$.

Now, thinking in terms of virtual attention heads, we have $(A_1\otimes V_1)(A_2\otimes V_2)(A_3\otimes V_3)=\left(A_1{A}_2{A}_3\right)\otimes \left(V_1{V}_2{V}_3\right)$. Since $A_1=A_3=I$, this simplifies to $A_2\otimes -W_1{E}_k{W}_2$.

When one does this analysis rigorously, there are three nuances we must add:

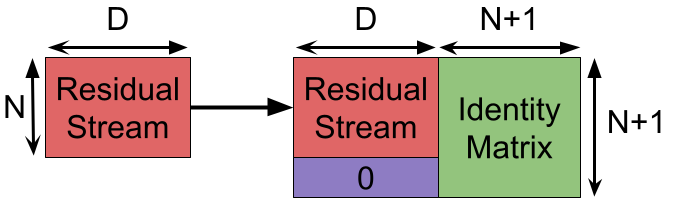
1. Since $W_1{E}_k{W}_2$ is size D-by-D, it must be padded out with 0s to make it side D’-by-D’ (here, $D^{\prime }=D+N+1$). That is $V=pad\left(W_1{E}_k{W}_2\right)$, where $pad\left(M\right)$ means “put matrix $M$ in the upper left corner of a new matrix and add 0s to make it the right-sized square matrix”.
2. Previously we computed $SiLU\left(x\right)=x\sigma \left(x\right)$ as $x-(1-\sigma (x\left)\right)x$, resulting in negative signs in $A_2$ and in $V_2=-E_k$. However, in this approach we compute $x\sigma \left(x\right)$ directly, so those negative signs go away.
3. The $A_2$ matrix computes attention patterns from the residual stream after it was modified by $W_1$, so the previous -1 entries are replaced with the $k$th column of the $W_1$ matrix. (No such accounting has to happen for the $A_3$ matrix, since we force $A_3$ to be the identity matrix no matter what.)

Summary

The resulting Q matrix for computing attention looks like this:

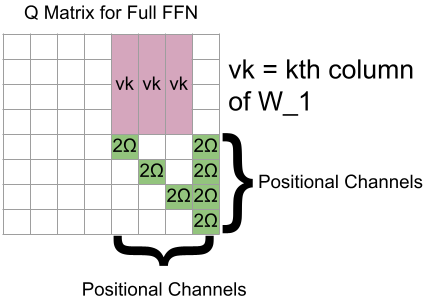
And as mentioned before, $V=pad\left(W_1{E}_k{W}_2\right)$, where $W_1$ and $W_2$ are the weight matrices for your FFN as before, and $E_k$ is the 4D-by-4D matrix with a 1 in the $(k,k)$th spot and a 0 elsewhere.

You use one such attention head for each of the 4D hidden dimensions. For GPT-3, that is a crushing 49152 attention heads in the FFN layer, compared to 96 attention heads in a normal attention layer. This a major slowdown compared to computing an FFN normally, although these attention heads could be parallelized.

Since we compute the hidden layers within the attention heads, we no longer need 4D extra dimensions in our model to store those values between steps. Now the model dimension is D+N+1 (the N+1 channels being used for 1-hot positional encoding). For GPT-3, that raises the dimensionality from 12288 to 14337, a 17% increase.

Demonstration Code

I’ve put Python code implementing this technique on github. Each of the now two components (FFNs, normal attention) are implemented both directly and with attention heads. They are tested on random matrices with $N=20$ and $D=30$, and the largest error entries in each matrix are on the order of ${10}^{-13}$. I have not tested how such errors propagate through multiple layers.

Conclusion

(To be read as a supplement to the conclusions in the previous post, which still stand.)

• [Epistemic status: high confidence] It is now somewhat more feasible to use this technique to augment transparency tools on transformers.
  • Compared to the previous technique, we have reduced the number of attention layers by a factor of 2x.
  • Compared to the previous technique, we have reduced the dimensionality of the residual stream by a factor of ~5x.
• [Epistemic status: high confidence] On GPT-3’s size hyperparameters, this technique would produce ~50k attention heads per FFN sublayer, more than 500x the number of attention heads in GPT-3’s classic attention layer!
  • [Epistemic status: high confidence] This gives a different perspective on the balance between attention heads and FFNs in LLMs.
    • Let us call traditional attention heads “external attention heads” (they pass information between word vectors), and the attention heads implementing FFNs “internal attention heads” (they pass information inside a word vector).
    • We’ve seen that external attention heads use 33% GPT-3’s parameters, and internal attention heads using 66% of the parameters.
    • But external attention heads are only 0.2% of all attention heads - the remaining 99.8% are internal attention heads.
  • This is a useful reminder that each hidden dimension in an FFN operates independently of the others, just as a group of attention heads work independently in parallel with each other.
  • [epistemic status: much less confidence than the rest of this post] It is possible that previous work “had much less success in understanding MLP layers so far” precisely because of this difference in scale - to study internal attention heads increases the number of attention heads by almost 3 orders of magnitude.
    • We could test this hypothesis if we had interpretability tools that work across multiple orders of magnitude. For example, if we had interpretability tools that work on 10000-headed attention-only transformers, we could apply them to 20-headed attention+FFN transformers, and expect roughly similar success in interpretability.
    • [Epistemic status: joke] I just had a great, extremely original idea for a slogan for such an interpretability paradigm: “scale is all you need”.