Interventions that increase the probability of Aligned AGI aren't the only kind of AGI-related work that could importantly increase the Expected Value of the future. Here I present a very basic quantitative model (which you can run yourself here) to start thinking about these issues. In a follow-up post I give a brief overview of extensions and analysis.

A main motivation of this enterprise is to assess whether interventions in the realm of Cooperative AI, that increase collaboration or reduce costly conflict, can seem like an optimal marginal allocation of resources. More concretely, in a utility framework, we compare

• Alignment interventions ($a_V$): increasing the probability that one or more agents have our values.
• Cooperation interventions given alignment ($a_{C|V}$): increasing the gains from trade and reducing the cost from conflict for agents with our values.
• Cooperation interventions given misalignment ($a_{C|\neg V}$): increasing the gains from trade and reducing the cost from conflict for agents without our values.

We used a model-based approach (see here for a discussion of its benefits) paired with qualitative analysis. While these two posts don't constitute an exhaustive analysis (more exhaustive versions are less polished), feel free to reach out if you're interested in this question and want to hear more about this work.

Most of this post is a replication of previous work by Hjalmar Wijk and Tristan Cook (unpublished). The basic modelling idea we're building upon is to define how different variables affect our utility, and then incrementally compute or estimate partial derivatives to assess the value of marginal work on this or that kind of intervention.

Setup

We model a multi-agentic situation. We classify each agent as either having (approximately) our values ($V$) or any other values ($\neg V$). We also classify them as either cooperative ($C$) or non-cooperative ($\neg C$).^[1] These classifications are binary. We are also (for now) agnostic about what these agents represent. Indeed, this basic multi-agentic model will be applicable (with differently informed estimates) to any scenario with multiple singletons, including the following:

• Different AGIs (or other kinds of singletons, like AI-augmented nation-states) interacting causally on Earth
• Singletons arising from different planets interacting causally in the lightcone
• Singletons from across the multi-verse interacting acausally

The variable we care about is total utility ($U$). As a simplifying assumption, our way to compute it will be as a weighted interpolation of two binary extremes: one in which bargaining goes (for agents with our values) as well as possible ($B$), and another one in which it goes as badly as possible ($\neg B$). The interpolation coefficient ($b$) could be interpreted as "percentage of interactions that result in minimally cooperative bargaining settlements".

We also consider all our interventions are on only a single one of the agents (which controls a fraction $F_I$ of total resources), which usually represents our AGI or our civilization.^[2] And these interventions are coarsely grouped into alignment work ($a_V$), cooperation work targeted at worlds with high alignment power ($a_{C|V}$), and cooperation work targeted at worlds with low alignment power ($a_{C|\neg V}$).

The overall structure looks like this:

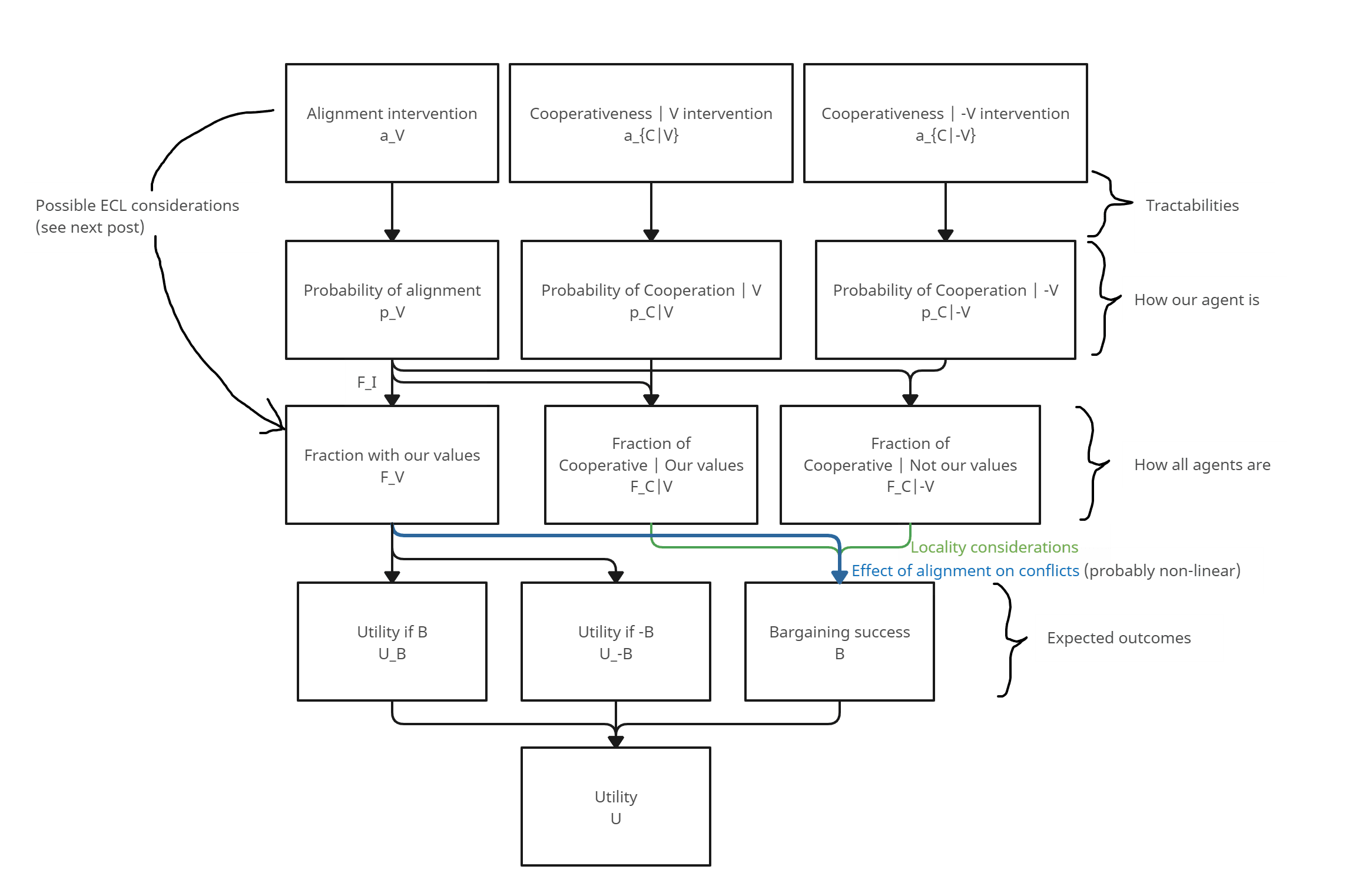
Full list of variables

This section safely skippable.

The first 4 variables model expected outcomes:

• $U_B\in R$: Utility attained in the possible world where our bargaining goes as well as possible.
• $U_{\neg B}\in R$: Utility attained in the possible world where our bargaining goes as badly as possible.
• $b\in [0,1]$: Baseline (expected) success of bargaining (for agents with our values), used to interpolate between $U_B$ and $U_{\neg B}$. Can be interpreted as "percentage of interactions that result in minimally cooperative bargaining settlements".
• $U\in R$: Total (expected) utility. We define it as the interpolation $U:=b\cdot U_B+(1-b)\cdot U_{\neg B}$

The next 3 variables model how the multi-agent landscape looks.

•  $F_V\in [0,1]$: Fraction (weighted by resources) of the agents that have our values.
• $F_{C|V}\in [0,1]$: Fraction (weighted by resources) of the agents having our values that are cooperative.
• $F_{C|\neg V}\in [0,1]$: Fraction (weighted by resources) of the agents not having our values that are cooperative.

The last 7 variables model how we can affect a single agent through different interventions.

• $F_I\in [0,1]$: Fraction (weighted by measure) that this single agent represents.
• $p_V\in [0,1]$: Baseline probability of said agent having our values.
• $p_{C|V}\in [0,1]$: Baseline probability of said agent being cooperative conditional on it having our values.
• $p_{C|\neg V}\in [0,1]$: Baseline probability of said agent being cooperative conditional on it not having our values.
• $a_V,a_{C|V},a_{C|\neg V}\in [0,1]$: Interventions affecting the above probabilities. We think of these as the fraction of our efforts that we spend on each kind of intervention.

Mathematical derivations

This section safely skippable.

Our goal is to estimate $\frac{dU}{da}$, given we have some values for $\frac{d{p}_V}{da},\frac{d{p}_{C|V}}{da}$ and  $\frac{d{p}_{C|\neg V}}{da}$  (tractability assessments).

By chain rule

$\begin{array}{}\frac{dU}{da}=\frac{dU}{d{F}_V}\frac{d{F}_V}{da}+\frac{dU}{d{F}_{C|V}}\frac{d{F}_{C|V}}{da}+\frac{dU}{d{F}_{C|\neg V}}\frac{d{F}_{C|\neg V}}{da}& \text{(}\star \text{)}\end{array}$

We begin by studying the 3 partial derivatives of U appearing in ($\star$).

For the first, product and chain rules give

$\begin{array}{c}\frac{dU}{d{F}_V}=\frac{db}{d{F}_V}(U_B-U_{\neg B})+b\frac{d{U}_B}{d{F}_V}+(1-B)\frac{d{U}_{\neg B}}{d{F}_V}\end{array}$

That is, changing the fraction of agents with our values can change the success of bargaining (first summand) and also the value of different scenarios (second and third summands).

For the second and third derivatives, we assume the fractions of cooperative agents can only affect bargaining success, but don't change the intrinsic value of futures in any other way. For example, it is not terminally good for agents to be cooperative (that is, the existence of a cooperative agent doesn't immediately increase our utility). Thus, all of $\frac{d{U}_B}{d{F}_{C|V}},\frac{d{U}_{\neg B}}{d{F}_{C|V}},\frac{d{U}_B}{d{F}_{C|\neg V}}$ and $\frac{d{U}_{\neg }B}{d{F}_{C|\neg V}}$ are 0. So again by product and chain and by these nullifications

$\begin{array}{c}\frac{dU}{d{F}_{C|V}}=\frac{db}{d{F}_{C|V}}(U_B-U_{\neg B})\end{array}$

$\begin{array}{c}\frac{dU}{d{F}_{C|\neg V}}=\frac{db}{d{F}_{C|\neg V}}(U_B-U_{\neg B})\end{array}$

We now turn to the other derivatives of ($\star$), which correspond to how our action changes the landscape of agents.

For the first, our action only changes the fraction of agents with our values by making our agent more likely to have our values^[3]:

$\begin{array}{c}\frac{d{F}_V}{da}=\frac{d{F}_V}{d{p}_V}\cdot \frac{d{p}_V}{da}=F_I\cdot \frac{d{p}_V}{da}\end{array}$

For the second one we get something more complicated. By chain rule

$\begin{array}{c}\frac{d{F}_{C|V}}{da}=\frac{d{F}_{C|V}}{d{p}_V}\frac{d{p}_V}{da}+\frac{d{F}_{C|V}}{d{p}_{C|V}}\frac{d{p}_{C|V}}{da}+\frac{d{F}_{C|V}}{d{p}_{C|\neg V}}\frac{d{p}_{C|\neg V}}{da}\end{array}$

Clearly $\frac{d{F}_{C|V}}{d{p}_{C|\neg V}}=0$, that is, changing the probability that our agent is cooperative if it were to not have our values won't alter in any case the fraction of agents with our values that are aligned.

But $\frac{d{F}_{C|V}}{d{p}_V}\ne 0$, since making your agent have your values could alter this fraction if your agent is atypically (un)cooperative. By considering $F_{C|V}=\frac{F_{C\cap V}}{F_V}$ and using the division rule we get

$\begin{array}{c}\frac{d{F}_{C|V}}{d{p}_V}=\frac{F_I}{F_V}(p_{C|V}-F_{C|V})\end{array}$

Intuitively, if our agent is atypically (un)cooperative, making it have our values will accordingly alter the proportion of cooperative agents with our values.

We deal with $\frac{d{F}_{C|V}}{d{p}_{C|V}}$ similarly by the division rule and obtain

$\begin{array}{c}\frac{d{F}_{C|V}}{d{p}_{C|V}}=\frac{F_I}{F_V}{p}_V\end{array}$

So in summary

$\begin{array}{c}\frac{d{F}_{C|V}}{da}=\frac{F_I}{F_V}(p_{C|V}-F_{C|V})\frac{d{p}_V}{da}+\frac{F_I}{F_V}{p}_V\frac{d{p}_{C|V}}{da}\end{array}$

For the third derivative we proceed analogously and obtain

$\begin{array}{c}\frac{d{F}_{C|\neg V}}{da}=-\frac{F_I}{1-F_V}(p_{C|\neg V}-F_{C|\neg V})\frac{d{p}_V}{da}+\frac{F_I}{1-F_V}(1-p_V)\frac{d{p}_{C|\neg V}}{da}\end{array}$

Finally, putting everything together in ($\star$) we obtain (grouped by intervention)

$\begin{array}{}\frac{dU}{da}=& \left[\right(U_B-U_{\neg B}\left)\right(\ast )+b\frac{d{U}_B}{d{F}_V}+(1-b\left)\frac{d{U}_{\neg B}}{d{F}_V}\right]F_I\frac{d{p}_V}{da}& & +& (U_B-U_{\neg B})\frac{db}{d{F}_{C|V}}{p}_V\frac{F_I}{F_V}\frac{d{p}_{C|V}}{da}& & +& (U_B-U_{\neg B})\frac{db}{d{F}_{C|\neg V}}(1-p_V)\frac{F_I}{1-F_V}\frac{d{p}_{C|\neg V}}{da}& & \text{(v)}& \text{(cv)}& \text{(c}\neg \text{v)}\end{array}$

where we have defined

$\begin{array}{c}(\ast )=\frac{db}{d{F}_V}+\frac{db}{d{F}_{C|V}}\frac{1}{F_V}(p_{C|V}-F_{C|V})-\frac{db}{d{F}_{C|\neg V}}\frac{1}{1-F_V}(p_{C|\neg V}-F_{C|\neg V})\end{array}$

When running simulations with $F_V$ very small, we might want to take it logarithmic for numerical stability.

Some discussion

What does bargaining success look like?

For starters, if interactions happen non-locally with respect to value systems (so that we are as likely to find ourselves interacting with agents having or not having our values), then we'd expect to benefit more from cooperation increases in bigger classes of agents. That is, $\frac{db}{d{F}_{C|V}}$ would be proportional to $F_V$ (usually small), and $\frac{db}{d{F}_{C|\neg V}}$ to $1-F_V$ (big), which would cancel out in (cv) and (c$\neg$v), resulting simply in the recommendation "intervene to make cooperative the kind of system most likely to happen".

But there might be locality effects, so that we are more likely to find ourselves in a trade situation with agents having our values (and that would partly counteract the above difference):

• This might happen because values are correlated with cognitive architecture, and agents find it easier to communicate with others with similar architectures (maybe due to simulations or saliency). But this effect would seem weak under a strong orthogonality thesis.
• This might also happen because of agents being more inclined to cooperate with similar values. Although this could also be modelled as terminally valuing some forms of cooperation (or disvaluing others), thus breaking our assumption that cooperation is not terminally (dis)valued.

Overall, thinking about locality by using the single variable $b$, which encompasses bargaining success both with similar and distant values, turns out to be clunky. In later extensions this is improved.

Another possible confounder is the effect of value coalition sizes on bargaining. For example, we could think that, holding cooperativeness constant, bigger value coalitions make bargaining easier due to less chaos or computational cost. In that case, going from 50% to 95% of agents having our values ($F_V$) would be stabilizing (and so $\frac{db}{d{F}_V}$ is positive in this regime), while going from 0% to 1% would be destabilizing ($\frac{db}{d{F}_V}$ negative). It's not even clear this should hold close to the extremes of $F_V$, since maybe when an almost-all-powerful coalition exists it is better for it to destroy the other small agents.

Maybe to account for this we could think of $F_V$ not as the distribution over "which AGIs / civilizations are created", but instead "the fraction under multi-agentic stability". That is, the distribution of those AGIs / civilizations after already waging any possible war with others. But that might not be a good approximation, since in reality war and cooperation are very intertwined, and not neatly temporally separated (and this might still be the case for AGIs).

While some of our final model's inputs can be informed by these coalition considerations, there doesn't seem to be an easy way around modelling coalition-forming more explicitly if we want good approximations.

We're also not yet including effects on cooperation from Evidential Cooperation in Large worlds (see the next post).

What do utilities look like?

$U_{\neg B}$ will vary a lot depending on, for example, how common we expect retributive or punitive actions to be.

$U_B$ will also vary a lot depending on your ethics (for example, how cosmopolitan vs parochial are your values) and opinions about the multi-agent landscape.

What do tractabilities look like?

We assume as a first simplification that the return on investment is linear, that is, $\frac{d{p}_V}{d{a}_V},\frac{d{p}_{C|V}}{d{a}_{C|V}}$ and $\frac{d{p}_{C|\neg V}}{d{a}_{C|\neg V}}$ are all constant.

This might not be that bad of an approximation (for marginal assessments) when, a priori, we are pretty uncertain about whether X more researcher-hours will lead to an unexpected break-through that allows for rapid intervention, or yield basically nothing. So the derivative should just be the expected gain linearly. But there are some instances in which this approximation fails more strongly, like when thinking about technical implementation work: We know a priori that we'll need to spend at least Y researcher-hours to be able to implement anything.

Implementation and extensions

You can toy with the model yourself here (instructions inside).

As mentioned above, it still seems like this bare-bones model is missing some important additional structure. Especially, estimating $U_B,U_{\neg B}$ and $b$ feels most ungrounded. This is discussed in the next post.

These two posts don't constitute an exhaustive analysis (more exhaustive versions are less polished), so feel free to reach out if you're interested in an all-things-considered assessment of the value of Cooperative AI work.

Work done at CLR's SRF 2023. Thanks to Tristan Cook and the rest of CLR for their help.

1. ^{^}

   For now, the definitions of $V$ and $C$ are left vague. In fact, in Hjalmar's basic model we are free to choose whichever concretization, as long as the same one informs our assessments of $U_B$ and $U_{\neg B}$. In latter extensions this was no longer the case and we worked with concrete definitions.

2. ^{^}

   Of course, this stops being the case in, for example, the multi-polar Earth scenario. In such cases we can interpret $F_I$ as an estimate of the fraction of agents (weighted by resources) our interventions can affect. Although some of the framings and intuitions below do overfit to the "single-agent" scenario.

3. ^{^}

   So we are ignoring some weird situations like "agents being more cooperative makes them notice our values are better".