Searching for Metatickle yielded this post and a bunch of paywalled papers whose previews used but didn't explain the term. Can you explain?
Indeed I tried to verify the connection but hit the same paywall :) I encountered the term in http://intelligence.org/files/TDT.pdf (p. 68, section 9.1). Yudkowsky discusses Metatickling rather briefly but it seems to be very close to what I'm doing here (but in decision theory terms).
Here are two relevant papers:
Eells - Metatickles and the dynamics of deliberation
Sobel - Metatickles, Ratificationism, and Newcomb-like problems without dominance
Related to: Intelligence Metrics and Decision Theories
Previously I presented a formalism for dealing with the Duality and Ontology problems associated with attempts to define a formal metric of general intelligence. It also solves the environment distribution problem. This formalism ran into problems closely related to the problems of decision theory. I tried to solve these problems using a formalization of UDT suitable for this context.
Here I'm going to pursue a different approach, which I believe to be analogous to the "metatickle" version of EDT. I will argue that, as opposed to decision theory, metatickling is a good approach to intelligence metrics. I will also present an analogous formalism for multi-agent systems. Finally, I will suggest an approach for constructing friendly utility functions using this formalism.
Review of Quasi-Solomonoff Distributions
In this section I will remind the idea behind quasi-Solomonoff distributions, glossing over mathematical details. For more details consult the previous article.
Most attempts at constructing a formal general intelligence metric are based on Legg and Hutter and involve considering an agent A interacting with an environment V through actions that A applies to V and observations A makes on V (the latter being information flowing from V to A). The problem with this is that such an agent is indestructible since no process in V can force a change in the inner workings of A. Thus an AI programmed in accord with this formalism will consider it an a priori truth that its mind cannot be tampered with in any way, an obviously false assumption.
In order to deal with this we can make A a part of V, as suggested by Orseau and Ring. This creates another problem, namely it's unclear what prior for V should we use. Legg and Hutter suggest using the Solomonoff distribution which makes sense since a perfectly rational agent is supposed to use the Solomonoff distribution as a prior. However, if A is a part of V, the Solomonoff distribution is clearly too general. For example if our A is implemented on a computing machine M, the rules according to which M works have to be part of our assumptions about V, since without making such assumptions it is impossible to program M in any sensible way.
Enters the quasi-Solomonoff distribution. Suppose you are a programmer building an AI A. Then it makes sense for you to impart to A the knowledge you have about the universe, including at least the rules according to which A's hardware M works. Denoting this knowledge (the tenative model) D, the distribution to use is the Solomonoff distribution updated by a period t of observing D-behavior, where the time parameter t represents your own certainty about D.
It is now tempting to introduce the intelligence metric
where {υi} is a sequence of natural numbers representing the universe Y, U is the utility function, Q is the data ("program") representing A and the expectation value is taken w.r.t. the quasi-Solomonoff distribution.
IEDT suffers from problems analogous to its associated decision theory EDT. Namely, suppose a certain Q is very likely to exist in a universe containing pink unicorns (maybe because pink unicorns have a fetish for this Q). Suppose further that pink unicorns yield very high utility, even though Q itself yields little utility directly. Then IEDT(Q) might be high even though Q has few of the attributes we associate with intelligence.
Alternatively we can introduce the intelligence metric
This time the expectation value is unconditional however we postulated a "divine intervention" which brings Q into existence at time t regardless of the physics selected from the quasi-Solomonoff distribution for Y. This unphysical assumption is an artifact analogous to the use of counterfactuals in CDT.
Metatickling
To make my way out of this conundrum I observe that the increase of probability of pink unicorns in the EDT example is "unjustified", since if you are a programmer building an AI then you know the AI came out the way it is because of you, not because of pink unicorns. One way to interpret this is that D isn't a sufficiently detailed model. However including a model of the AI programmer into D seems impractical. Therefore I suggest instead including a generic intelligence optimization process O.
Denote) the probability assigned by the quasi-Solomonoff distribution to program R as the physics of Y. Then, the metatickle quasi-Solomonoff distribution assigns to R the probability
the probability assigned by the quasi-Solomonoff distribution to program R as the physics of Y. Then, the metatickle quasi-Solomonoff distribution assigns to R the probability
Here Z is a normalization factor, β is a constant representing O's power of optimization, ER is expectation value in an R-universe and I is the yet unspecified intelligence metric (yep, we're going self-referential).
The metatickle intelligence metric is then defined as the solution to the equation
where the expectation value is taken w.r.t. the metatickle quasi-Solomonoff distribution defined by D and IβMTDT.
It is suggestive to apply some fixed-point theorem to get results about existence and/or uniqueness of IβMTDT, something I haven't done yet.
Metatickle EDT suffers from a problem common with CDT, namely it two-boxes on Newcomb's problem. The same applies here. Specifically, suppose Ω is a superintelligence which is able to predict Q by modeling O and it places utility in the first box iff A(Q) one-boxes. Then two-boxers are assigned high intelligence for the self-referential reason that Ω predicts this and leaves the first box empty. However, I claim that in this context this behavior is sensible. From A(Q)'s point-of-view, it would gain nothing by one-boxing since one-boxing would only mean Q came out with a statistical fluke and Ω still left the first box empty (since the fluke is unpredictable). From O's point-of-view, it is doing everything right since its purpose is maximizing intelligence, not utility. O behaves just like the philosophy students Yudkowsky likes to describe, which prefer winning arguments over winning money. Indeed, we can consider a situation in which Ω would generate utility on the condition that Q is made unintelligent. In this case there is nothing paradoxical about the resulting negative relation between intelligence and utility. This argument seems similar to the standard defense of CDT: "Ω simply discriminates in favor of irrational behavior". However, the standard counterargument "it isn't discrimination as long as only the final decisions are involved rather than the intrinsic process leading to the decisions" doesn't apply here, since from O's point-of-view Q is a final decision.
Note that MTDT-intelligent agents cope fantastically with the usual Newcomb's problem. That is, if Ω prepares the boxes after formation of A (moment t) then an MTDT-intelligent A will one-box (ceteris paribus i.e. ignoring possible non-decision-theoretic effects of programming A in this way).
Note also that it doesn't mean we can use ICDT just as well. CDT-intelligent agents suffer from a severe mental disability, namely they are unable to deduce anything about the universe from the properties of their own self. They are blinded by faith in a divine intervention which created them. This problem doesn't apply to IMTDT.
It seems useful to let β go to infinity, which corresponds to "perfect" O. I suspect I∞MTDT converges in many cases. In this limit the "pink unicorn" effect is likely to entirely disappear, since for highly intelligent Q any hypothesis of Q's origin that doesn't involve something that looks like an actual intelligence optimization process would be suppressed by its complexity.
Multi-Agent Systems
It is also interesting to consider a system of N agents Ak(Qk), each with its own utility function Uk and program Qk encoded in the universe as qk(υt). In this case the metatickle quasi-Solomonoff distribution is defined by
and we have the system of equations
The functions Ik define a game and it's interesting to study e.g. its Nash equilibria.
In this case the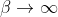 limit is more complicated since depending on the relative speed of growth of the different β's, there might be different results.
limit is more complicated since depending on the relative speed of growth of the different β's, there might be different results.
Friendly Utility Functions
The problem of constructing a friendly utility function can be regarded as inverse to the problem of constructing strong AI. Namely the latter is creating an optimal agent given a utility function whereas the former is finding the utility function of the agent which is already known (homo sapiens).
Fix a specific agent Alice, w.r.t. which the utility functions should be friendly. Our prior for Alice's unknown utility function U will be that it's computed by some uniformly distributed program T (like in the definition of the Solomonoff distribution). The information we use to update this prior is that Alice was generated by an intelligence optimization process of power β, i.e. she was selected from a metatickle quasi-Solomonoff distribution corresponding to U. We then take the expectation value U*(Alice) of the resulting distribution on utility functions1.
It is not so clear how to determine β. Evidently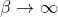 is not a good approach here since we don't consider humans to be optimal for their own terminal values. A possible solution is to postulate a Solomonoff-type prior for β as well.
is not a good approach here since we don't consider humans to be optimal for their own terminal values. A possible solution is to postulate a Solomonoff-type prior for β as well.
1It might fail to converge. To remedy this, we can restrict ourselves to utility functions taking values in the interval [0, 1].