If you're going to use anthropic probability, use the self indication assumption (SIA) - it's by far the most sensible way of doing things.
Now, I am of the strong belief that probabilities in anthropic problems (such as the Sleeping Beauty problem) are not meaningful - only your decisions matter. And you can have different probability theories but still always reach the decisions if you have different theories as to who bears the responsibility of the actions of your copies, or how much you value them - see anthropic decision theory (ADT).
But that's a minority position - most people still use anthropic probabilities, so it's worth taking a more through look at what SIA does and doesn't tell you about population sizes and conditional probability.
This post will aim to clarify some issues with SIA, especially concerning Jaan Tallinn's simulation-tree model which he presented in exquisite story format at the recent singularity summit. I'll be assuming basic familiarity with SIA, and will run away screaming from any questions concerning infinity. SIA fears infinity (in a shameless self plug, I'll mention that anthropic decision theory runs into far less problems with infinities; for instance a bounded utility function is a sufficient - but not necessary - condition to ensure that ADT give you sensible answers even with infinitely many copies).
But onwards and upwards with SIA! To not-quite-infinity and below!
SIA does not (directly) predict large populations
One error people often make with SIA is to assume that it predicts a large population. It doesn't - at least not directly. What SIA predicts is that there will be a large number of agents that are subjectively indistinguishable from you. You can call these subjectively indistinguishable agents the "minimal reference class" - it is a great advantage of SIA that it will continue to make sense for any reference class you choose (as long as it contains the minimal reference class).
The SIA's impact on the total population is indirect: if the size of the total population is correlated with that of the minimal reference class, SIA will predict a large population. A correlation is not implausible: for instance, if there are a lot of humans around, then the probability that one of them is you is much larger. If there are a lot of intelligent life forms around, then the chance that humans exist is higher, and so on.
In most cases, we don't run into problems with assuming that SIA predicts large populations. But we have to bear in mind that the effect is indirect, and the effect can and does break down in many cases. For instance imagine that you knew you had evolved on some planet, but for some odd reason, didn't know whether your planet had a ring system or not. You have managed to figure out that the evolution of life on planets with ring systems is independent of the evolution of life on planets without. Since you don't know which situation you're in, SIA instructs you to increase the probability of life on ringed and on non-ringed planets (so far, so good - SIA is predicting generally larger populations).
And then one day you look up at the sky and see:

After seeing this, SIA still increases your probability estimate for large populations on ringed planets - but your estimate for non-ringed planets reverts to the naive baseline. SIA can affect variables only as much as they are correlated with the size of the minimal reference class - as variables become more independent of this, SIA's effect becomes weaker.
Once you know how all about yourselves, SIA is powerless
Designate by P the naive probability that you might have, before considering any anthropic factors. Let PSIA be the anthropic probability, adjusted by SIA. If N is a random variable that counts the size of the minimal reference class, then SIA's adjustment for any random variable X is:
PSIA(N=n and X=x) = nP(N=n and X=x)/Norm
This is just rephrasing the fact that we weight the worlds by the size of the minimal reference class. The normalization term "Norm" is simply a constant that divides all PSIA probabilities to ensure they sum to 1 after doing the above adjustment (Norm is equal to the expected value of N). If X is independent of N (and hence P(X=x) doesn't have any anthropic correction from SIA, and equals PSIA(X=x)), then conditional probability follows the rule:
PSIA(N=n|X=x) = PSIA(N=n and X=x)/PSIA(X=x) = nP(N=n and X=x)/(Norm*P(X=x)) = nP(N=n|X=x)/Norm
If X isn't independent of N, then PSIA(X=x) is not necessarily the same as P(X=x), and the above equality need not hold. In most cases there will still be an anthropic correction, hence:
- In general, the probability of anthropic variables conditioned upon other variables will change under SIA.
The picture is very different, however, if we condition on anthropic variables! For instance if we condition on N itself, then PSIA is exactly the same as P, as there are two factors of n (and two Norms) cancelling out:
PSIA(X=x|N=n) = PSIA(N=n and X=x)/PSIA(N=n) = nP(N=n and X=x)/nP(N=n) = P(X=x|N=n)
Hence:
- The probability of any variable conditioned on the size of the minimal reference class, is unaltered by SIA.
So if we condition on the size of our reference class, there are no longer any anthropic effects.
I myself was somewhat confused by this (see here and here). But one implication is that, if you know the past human population, you expect the current human population to be above trend. Ditto if you know the future population: you then expect the current population to be higher than that information would naively imply (this gives you a poor-man's Doomsday argument). But if, on the other hand, you know your current population, then you expect future and past populations to be given by naive probabilities, without anthropic adjustment.
To illustrate this counterintuitive idea, take a toy model, with three populations at three steps (entitled "past population", "present population" and "future population"). Imagine that the past population was 3, and that the population either goes up by one, goes down by one, or stays the same, with equal (naive) probability. So we now have nine equally probable population series: (3,2,1), (3,3,3), (3,4,4), (3,4,5), etc...
We live in the present, and we will adjust these series with SIA; thus we have three series (3,4,3), (3,4,4) and (3,4,5), each with probability 4/27, three series (3,3,4), (3,3,3) and (3,3,2), with probability 3/27, and three series (3,2,3), (3,2,2) and (3,2,1), with probability 2/27. Then if I give you the past and future population values, you expect the current population to be higher than the average: (3,?,3) is more likely to be (3,4,3), (3,?,2) is more likely to be (3,3,2), and so on. The only exceptions to this are (3,?,5) and (3,?,1), which each have only one possible value.
However, if I give you the current population, then all possible future populations are equally likely: (3,4,?) is equally likely to end with 3, 4, or 5, as the sequences (3,4,3), (3,4,4) and (3,4,5) are equally likely. And that is exactly what naive probability would tell us. By conditioning on current population (indirectly conditioning on the size of the minimal reference class), we've erased any anthropic effects.
Jaan Tallinn's tree
If you haven't already, go an watch Jaan Tallinn's presentation. It's beautiful. And don't come back until you're done that.
Right, back already? Jaan proposes a model in which superintelligences try and produce other superintelligences by evolving civilizations through a process of tree search. Essentially evolving one civilization up to superintelligence/singularity, rewinding the program a little bit, and then running it forwards again with small differences. This would cut down on calculations and avoid having to simulate each civilization's history separately, from birth to singularity.
Then if we asked "if we are simulated, where are we likely to exist in this tree process?", then SIA gives you a clear answer: at the final stage, just before the singularity. Because that's where most of the simulated beings will exist.
But the real question is "if we are simulated, then given that we observe ourselves to be at a certain stage of human civilization, how likely is it that we are at the final stage?" This is a subtly different question. And we've already seen that conditioning on variables tied to our existence - in this case, our observation of what stage of civilization we are at - can give very different answers from what we might expect.
To see this, consider five different scenarios, or worlds. W1 is the world described in Jaan Tallinn's talk: a branching process of simulations, with us the final stage before the singularity. In our model, it has eight civilizations at the same stage as us. Then we have world W2, which is the same as W1, except that there's still another stage remaining before the singularity: we add extra simulations at a date beyond us (which means that W2 contains more simulations that W1). Then we have W3, which is structurally the same as W2, but has the same total number of simulations as W1. The following table shows these worlds, with a dotted rectangle around civilizations at our level of development. Under each world is the label, then a row showing the number of civilizations at our level, then a row showing the number of civilizations at every stage.
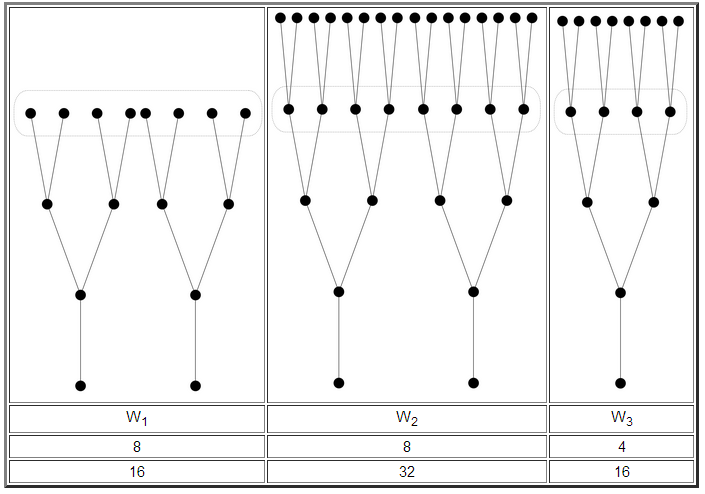
But maybe the tree model is wrong, and the real world is linear - either because the superintelligences want to simulate us thoroughly along one complete history, or maybe because most agents are in real histories and not simulations. We can the consider world W4, which is linear and has the same number of civilizations at our stage as W1 does, and W5, which is linear and has the same total number of civilizations as W1 does:
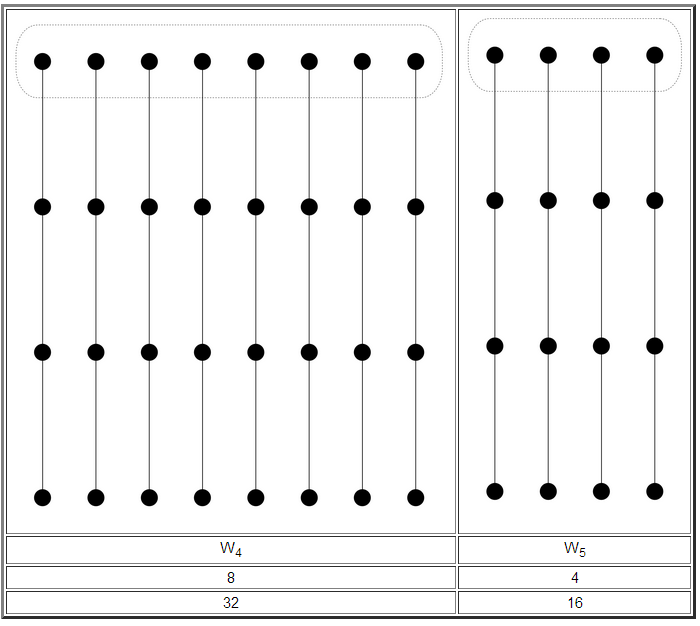
What is the impact of SIA? Well, it decreases the probabilities of worlds W3 and W5, but leaves the relative probabilities of W1, W2 and W4 intact. So if we want to say that W1 is more likely than the others - that we are indeed in the last stages of a simulation tree search - we can only do so because of a prior, not because of SIA.
What kind of prior could make this work? Well, we notice that W2 and W4 have a higher total population that W1. This feels like it should penalise them. So a reasonable prior would be to consider total population size and type of world are independent variables. Then if we have a prior over population that diminishes as the population increases, we get our desired result: worlds like W2 and W4 are unlikely because of their large populations, and worlds like W3 and W5 are unlikely because of SIA.
Is this enough? Not quite. Our priors need to do still more work before we're home and dry. Imagine we had a theory that superintelligences only simulated people close to the singularity, and used general statistical methods for the previous history. This is the kind of world that would score highly by SIA, while still having a low total population. So we better make them very unlikely a priori, lest they swamp the model. This is not an unreasonable assumption, but is a necessary one.
So far, we've been using "total population at our current era" as a constant multiple of N, the size of the minimal reference class, and using the first as a proxy for the second. But the ratio between them can change in different worlds. We could imagine a superintelligence that only produced human civilizations. This would get a tremendous boost by SIA over other possibilities where it has to simulate a lot of useless aliens. Or we could go to the extreme, and imagine a superintelligence dedicated manically to simulating you, and only you, over and over again. Does that possibility feel unlikely to you? Good, because our extreme prior unlikelyhood is the only thing from preventing SIA blowing that scenario up until it dominates all other possibilities.
Conclusion
So anthropic reasoning is subtle, and especially when we are conditioning on facts relevant to our existence (such as observations in our world), we need to follow the mathematics rather than our intuitions - and count on our priors to do a lot of the heavy lifting. And avoid infinity.