Introduction

Andrew Critch has recently written about how respect for boundaries are norms that, to some extent, should convergently arise. 

In this post, I want to link the concept of boundary preservation to active inference and, more importantly, game theory to show that it indeed makes sense for boundaries to be preserved over time. 

We will look at Daniel Dennett’s reasoning for humans wanting an intact sense of “free will” as an example of a boundary. 

An important point for the entire conversation of boundaries is that it is implicitly contained within an evolutionary or decision-theoretic frame. So we will go one meta-level up and talk about the optimality for individuals within environments with or without boundary-specific coordination norms. We will conclude that boundaries are isomorphic to coordination norms in multi-agent iterated prisoner's dilemmas. 

Negotiation & Free Will

In his book Intuition Pumps and other tools for Thinking, Daniel Dennett asks why free will is such an essential concept for humans. The answer that he comes up with goes something like the following:

Imagine you’re selling a computer to someone else; you bought it for 1000$ two years ago and want somewhere around 500-800$ for it. The other person is willing to buy it for 400-600$ depending on what you give as an initial offer. In a normal situation, you might get a price of 550$ for the computer. 

Let’s now imagine that the person you’re negotiating with has a great sense of social cues and notices that you’re happy about the trade. They might now push you even further and get the price lower. Why did this happen? They got a glimpse into the decision process in your head so they could model you and predict what price you would have wanted. 

They were then able to predict what you were going to do in the future. 

This is an example relevant to what Dennett believes the entire fuzz in the debate on free will is about, a boundary that retains our internal thoughts or, in <<Boundaries>> speak, defends our viscera from infiltration from the external world. 

Angle Shooting In Poker

Let’s now look at another real-world example of this happening and what relation that has with boundary preservation.

In poker, there’s a phenomenon known as “angle shooting”; this is when someone does something deceptive to gain information from other players. An example of this is doing an incomplete call, where you pretend like you called whilst you didn’t put in the total amount. This is an example of breaking the perceived boundary of the other player. 

Some might say this is a social and not a personal boundary, but the difference between the two isn’t clear. This is something that we can resolve if we introduce the definition of the preservation conditions for the boundary that Critch brings forth. 

Infiltration & Exfiltration

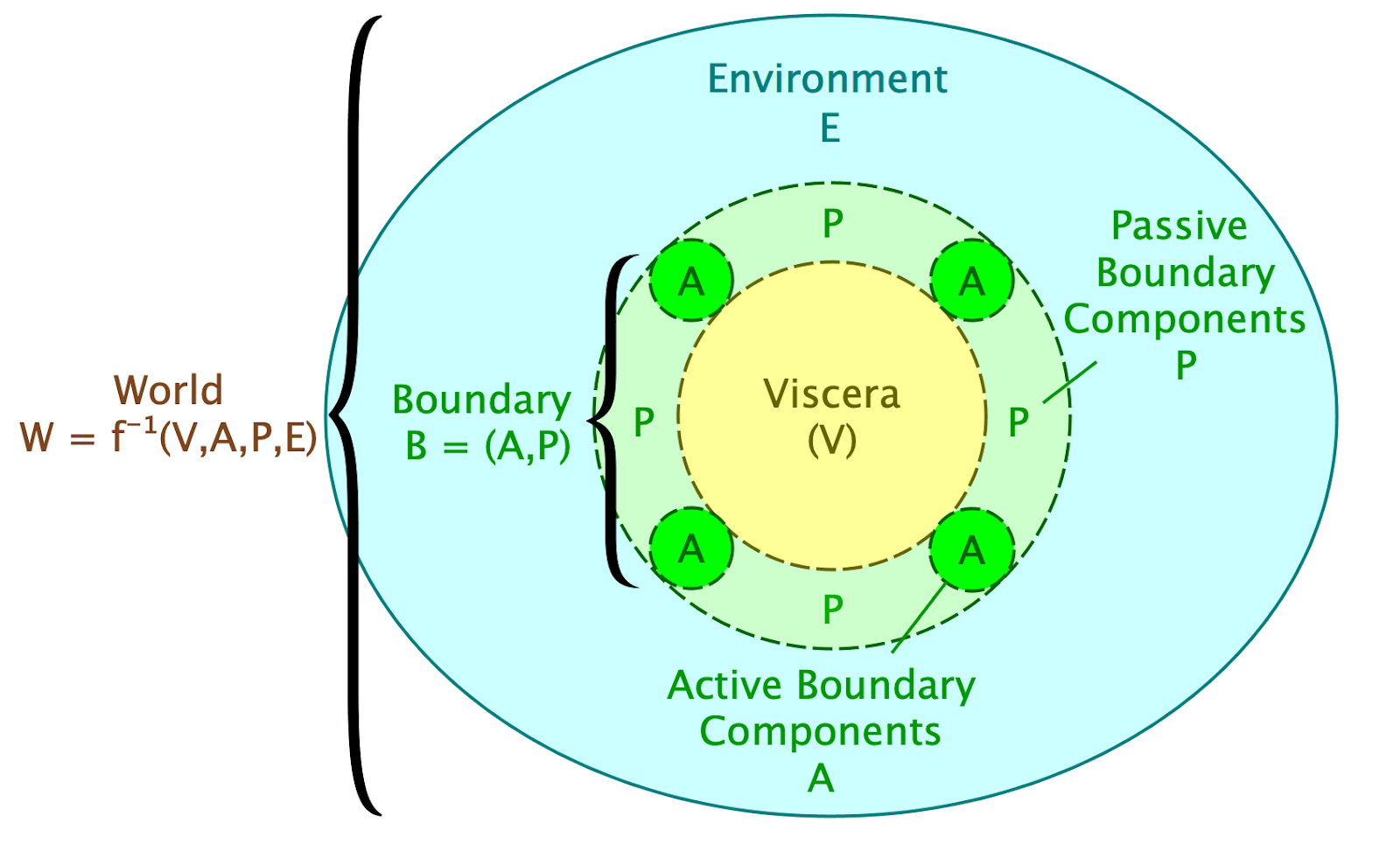
Let’s first and foremost introduce Critch’s model of boundary preservation really quickly. The picture that Critch has in mind when it comes to boundaries is the following: 

The important parts for our model is the passive and active boundary components and how they interact with the world. This is because they determine the shape of the boundary.

If a function describes something well, the difference between the predictions of what the world does and what the world actually does should be small, which is what Critch describes as the definition of how the boundaries should look like: 

Next, we need another function $Ag{g}^{\prime }$ for aggregating description error over time, e.g., max or avg.  Here $Ag{g}^{\prime }$ may or may not be the same as the previous $Agg$ function, but there should be some relationship between them such that bounding one can bound the other (e.g., if they're both Avg or Max then this works).  For any such function $Ag{g}^{\prime }$, define an aggregate description error function as

• ${ADE}_{\sigma ,\tau }\left(r\right):=\underset{\sigma \le t<\tau }{Ag{g}^{\prime }}DErr(T_t,r)$ 

We say $r_{\theta }$ is a good fit for the time interval $[\sigma ,\tau )$ if ${ADE}_{\sigma ,\tau }\left(r_{\theta }\right)$ is small.  This implies several things:

1. infiltration can't be too large in that time interval, i.e., the boundary remains fairly well intact;
2. for each $t$, $(V_t,A_t)$ do not destroy the present or subsequent validity of $r_{\theta }$ too badly, i.e., the system "makes sufficiently self-preserving choices"; and

Thus, if $r_{\theta }$ is a good fit, then 1 & 2 together say that the decisions made by $r_{\theta }$ will perpetuate the four defining properties (a)-(d) of the definition.  

So what is “Infiltration” then? Well it is how much the Active boundary is different from the surrounding environment between any two time steps. The “Exfiltration” is the amount of the Viscera that exists in the surrounding environment and passive boundary at any two timesteps. 

The following picture would be an inadequate representation of the viscera for an ellipsoid. 

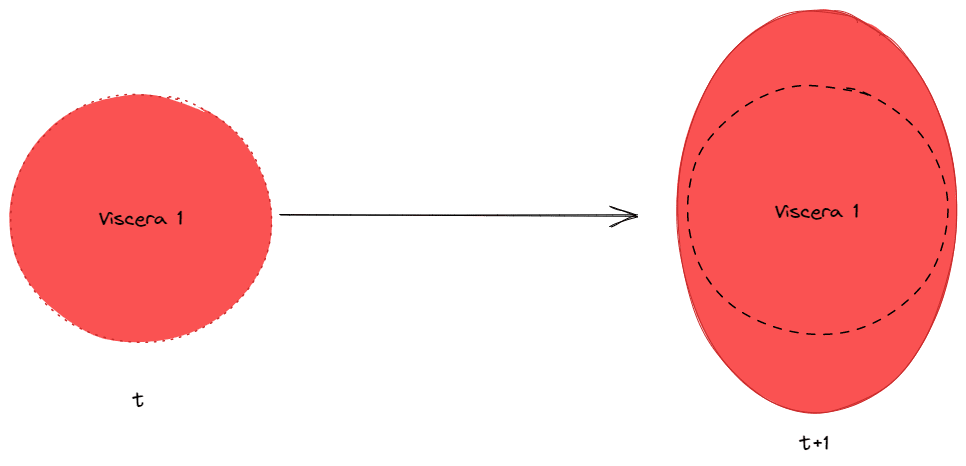
At timestep t+1, the object obviously has a viscera that’s outside the boundary. You can imagine that this is the same as Critch’s definition but that the definition he provides is focused on the decision rules and how well it predicts action, whilst this is the underlying geometric representation.

Let's see how it fits in with Critch's definition:

1. "Infiltration" of information from the environment into the active boundary & viscera:
   $Infil\left(\varphi \right):=\underset{t\ge 0}{Agg}\underset{W^{\omega }\sim \varphi }{Mut}((V_{t+1},A_{t+1});E_t\mid (V_t,A_t,P_t))$
2. "Exfiltration" of information from the viscera into the passive boundary & environment:
   $Exfil\left(\varphi \right):=\underset{t\ge 0}{Agg}\underset{W^{\omega }\sim \varphi }{Mut}((P_{t+1},E_{t+1});V_t\mid (A_t,P_t,E_t))$

We can see infiltration as the amount of information shared between our viscera, and active boundary pair with the environment and exfiltration as the amount shared between the passive boundary viscera pair and the environment. 

And in our case, it means that the viscera has expanded past the boundary, which leads to it sharing information with the environment in a way that is not through the boundary. Meaning that the mutual information between the viscera at timestep t+1 and the environment at t is larger than zero. This would mean that information on the viscera is both exfiltrated and infiltrated at the same time with the drawn boundary. 

We can also draw boundaries in ways where the exfiltration is zero whilst the infiltration is non-zero and vice versa. 

Solving angle shooting

So back to the question, what type of boundary-breaking is angle shooting? 

For each timestep, the agent has to make two decisions, how it should model its viscera and what action it should take. How should these change over time? Critch describes the math behind how we can do this in his post and so I won’t repeat the details. 

For us, the important part is that the boundary definition is a descriptive model that is rated on how well it fits the matched data or KL divergence. 

In the definition, there’s no defining way boundaries should manifest, which is both a blessing and a curse. Since it is more general, it is uncertain how we should implement it in the real world, which can make it confusing. In a later post, I will try to give my take on how we can combine the more computational side of this, which is related to finite factored sets to a more coherent definition. (My epistemic status on if this will work is currently uncertain)

The viscera will adapt to the most optimal shape for it to be at any point in time. This is part of the decision rule that we have defined. This means that the viscera will optimise for usefulness at the same time that it also tries to remain consistent. 

My intuition on how boundaries are preserved over time is based on how I think of the viscera. The viscera in a Bayesian frame are the assumptions that we make about the world that aren’t likely to change in the future. Usually, these are things that we have close to full causal control over, such as your hand or other things that most likely won’t change in the future unless a guy is holding an axe telling you that he will chop off your hand next to you. 

In other words, the things preserved by the viscera are the things that don’t have high uncertainty in them. Therefore things with low chaos or environments with high predictability mean that you can extend your viscera to account for high predictability. 

What happens when someone angle shoots you is then that the boundary is broken, and then the KL divergence will be a lot higher as it wasn’t part of your future predicted worlds. The more you thought the boundary was stable, the higher the KL divergence will be, and so if you, for example, come home to an unfaithful partner, this will most likely be a huge shock to your system. 

If you believe that you’re in an environment with high predictability, then you will extend your viscera to assume that environment E will look the same as your prediction of it. The perspective here is one of that the boundary formation around viscera should be predicated by the amount of chaos in the environment. The higher the predictability, the higher chance that the viscera remains intact. 

Or in one phrase: Stable environments besets stable boundaries.

It is then not a question of whether the viscera is part of your personal space or not, it’s instead a question of how predictable the environment seems to be. (hopefully, more on this in a later post) Let’s look at why respect for boundaries seems to be an integral part of society. Let’s look at our poker table again and take a meta-perspective. 

If the rest of the table allows that person to keep defecting, then you know you’re in a group of people who allow deception, which means that you can’t trust the other people there. What is the advice, then? Leave the table and go to another poker table where the norms are kept. 

This then means that you will leave the defecting players to go play with the cooperating ones. It is not hard to see the isomorphism to the underlying mechanics of iterated prisoner’s dilemmas and how cooperating environments outcompete defecting ones. 

As a consequence, environments where people don’t angle shoot, will be the ones that are optimal for an agent to be in, and such environments will therefore be the convergent ones. Not breaking boundaries is optimal because it allows for the integrity of internal world models, which ensures that we minimise the expected free energy of the future, which all agents that persevere in an optimisation system must do according to Active Inference.

In terms of <<Boundaries>>, high-trust environments allow the viscera to be expanded to encompass more than just the agent; it can also encompass how other agents will behave around them. 

Conclusion

In conclusion, Andrew Critch's concept of boundary preservation and its relation to active inference and free energy minimisation provide valuable insights into why respecting other people's boundaries is not only a social norm but an optimal strategy for agents to maintain their internal world models. 

High-trust environments that foster respect for boundaries lead to more stable and predictable interactions, allowing agents to minimise the expected free energy of the future (or whatever equivalent optimisation metric you want), ultimately optimising their decision-making process. As a result, environments where boundaries are respected and upheld will be more attractive and beneficial for agents to inhabit, leading to their convergence and proliferation. 

More importantly, when we look at it from an Active Inference perspective, we can see boundaries as ways of modularising the world to make it more predictable. If someone breaks the norms of, for example, not angle shooting in poker, it makes your future world model more uncertain. You would then be outcompeted by a person in an environment where this doesn’t happen, and there is, therefore, selection pressure towards boundary norms.