Summary. Thoughts arising from doing calibration training on ~500 questions, consisting of both trivia questions and mundane real life events.

Epistemic status: Confident on own experiences, uncertain on generalizability and usefulness to others. 

Intro

I've practiced quantifying my uncertainty via assigning numerical probabilities for my beliefs. I've used Open Philanthropy's web app and Quantified Intuition's question set for calibration training (doing ~250 questions on both), and also have made predictions on ~100 real life every-day events. Below I share a few things I learned from this.

I assume no further background beyond knowing what calibration training is, though without experience in calibration practice one may not get much insight from the post.

I. Learning to be calibrated is not that hard

This often-repeated point is worth repeating: you can learn to be calibrated.

There was a time when I first read texts like Kahneman's Thinking, Fast and Slow, explaining how people generally are grossly overconfident and how this is true also for Highly-Educated Smart People and People Who Should Know Better. Some part of me thought that "What?! I'm pretty sure my 98% confidence intervals wouldn't be wrong 40 percent of the time!", and another part thought along the lines of (what I now recognize is) modest epistemology.

Much later, I tried out calibration training. Sure, my first attempt was not great, but it wasn't that bad either. And then I did a bit more training, and 75% of my 80% assessments (n = 63), or 56% of my 60% assessments (n = 101), were correct.^[1]

Caveats: My calibration feels poorer when changing the question category (e.g. "doing EA-themed calibration questions" and "predicting everyday events" are very different), and getting up to speed requires a bit of practice and feedback in the new environment. Also, the tools I used informed me about the correctness of my answers immediately after each answer (instead of after a batch of 100 questions or such); this feedback loop feels crucial to me, as I get some feeling about how I'm doing in real time. I could very well see myself being way off in a new environment without a feedback loop.^[2]

II. >90% region is difficult

Making confident claims feels difficult: I really don't think I'm well calibrated in the >90% region. 

Example: Once I made a 90% prediction for "I still have peanut butter left back at home". I was correct. In retrospect I should have been much more confident: I knew that I had some left, would have remembered if I had run out, had just eaten some a couple of days ago, and so on. I don't know what is the "right" probability that I should assign in such cases, but it sure is a lot higher than 90%.

There seem to be several things at play here, such as loss aversion ("what if I make a 95% prediction and I'm wrong (gasp!)"), being afraid of overconfidence, and lack of training on the category of things I "know".

So while my probabilities aren't actually 0 or 1, I now recognize better the areas where I'm better off by simply thinking in binary terms of knowledge and deductive logic instead of probability theory.

III. No safe defense, not even Laplace's rule

One day, I went to eat lunch at my university's cafeteria. They had oranges for dessert. Next day, they also had oranges. I decided to predict whether on the third day they would also serve oranges.

Laplace's rule of succession says that, if you don't know anything else, you should guess 75%. Now, 75% did feel high to me, so I moved down and guessed 60%.

The following day the cafeteria served pears.

I thought about it and realized what went wrong^[3]. I had gone to the cafeteria dozens of times before and had some vague impression of how often they serve which fruits. However, I didn't feel like doing the mental effort of actually thinking of the numerical frequencies or the dependencies between consecutive days (maybe the cafeteria aims for variation).

So I resorted to I Just Don't Know, which then allows me to apply Laplace's rule (right?).^[4] But after noticing the higher-than-expected-probability, I decided to subtract a bit.

...and that's not how this works.

Next time when I don't feel like actually applying numerical methods in a sane way, I will just go with my intuition instead of applying a bogus method and getting anchored on a bogus number.

IV. An anomaly

When looking at the results of my predictions for real-world events, I noticed that my 67% predictions were way off. On the 10 events I had put a 2/3 probability on, only three happened (in contrast to the expected 6.7).

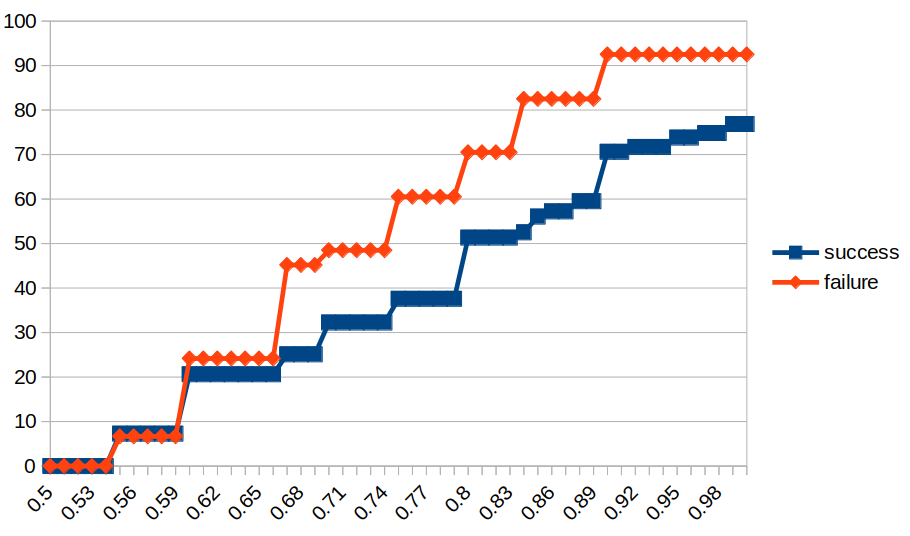
What's going on? It's not that I'm overall bad - remove the 2/3 predictions and I'm well calibrated. The hypothesis "I just got unlucky" isn't a good explanation either^[5].

I looked at the ten 2/3 predictions, and I found a common pattern lying underneath many of them. It's hard to communicate it without providing lots of context, but my one-sentence-summary is

"There is a mental motion I use in situations where I [can't model the situation well / can't find reference classes or analogous cases / have conflicting intuitions], just decide to go with my gut, and that mental motion outputs a probability of 2/3." 

And this procedure results in wrong predictions more often than 1/3 of the time, in fact possibly more often than 50%.

From now on I'll think twice if I feel like assigning 2/3 to something.

1. ^{^}

   These results were obtained with this tool.

2. ^{^}

   When I did pastcasting, I systematically thought that things happen more often than they actually did. (I recall reading that in Metaculus around 35-40 percent of predictions resolve as true; I guess the same holds here and that threw me off.)

3. ^{^}

   Sure, being wrong on a 60% prediction is not terrible, but there was a lesson to be learned here.

4. ^{^}

   Applying Laplace's rule in particular throws away the information that there are more than two different types of fruits! See Laplace's rule for multiple outcomes.

5. ^{^}

   The p-value, i.e. P(I got at most 3 correct | I am perfectly calibrated), is 0.02.