79
Ω 32
I was at the NeurIPS many-shot jailbreaking poster today and heard that defenses only shift the attack success curve downwards, rather than changing the power law exponent. How does the power law exponent of BoN jailbreaking compare to many-shot, and are there defenses that change the power law exponent here?
Circuit breaking changes the exponent a bit if you compare it to the slope of Llama3 (Figure 3 of the paper). So, there is some evidence that circuit breaking does more than just shifting the intercept when exposed to best-of-N attacks. This contrasts with the adversarial training on attacks in the MSJ paper, which doesn't change the slope (we might see something similar if we do adversarial training with BoN attacks). Also, I expect that using input-output classifiers will change the slope significantly. Understanding how these slopes change with different defenses is the work we plan to do next!
Nice work! It's surprising that something so simple works so well. Have you tried applying this to more recent models like o1 or QwQ?
For o1-mini, the ASR at 3000 samples is 69.2% and has a similar trajectory to Claude 3.5 Sonnet. Upon quick manual inspection, the false positive rate is very small. So it seems the reasoning post training for o1-mini helps with robustness a bit compared to gpt-4o-mini (which is nearer 90% at 3000 steps). But it is still significantly compromised when using BoN...
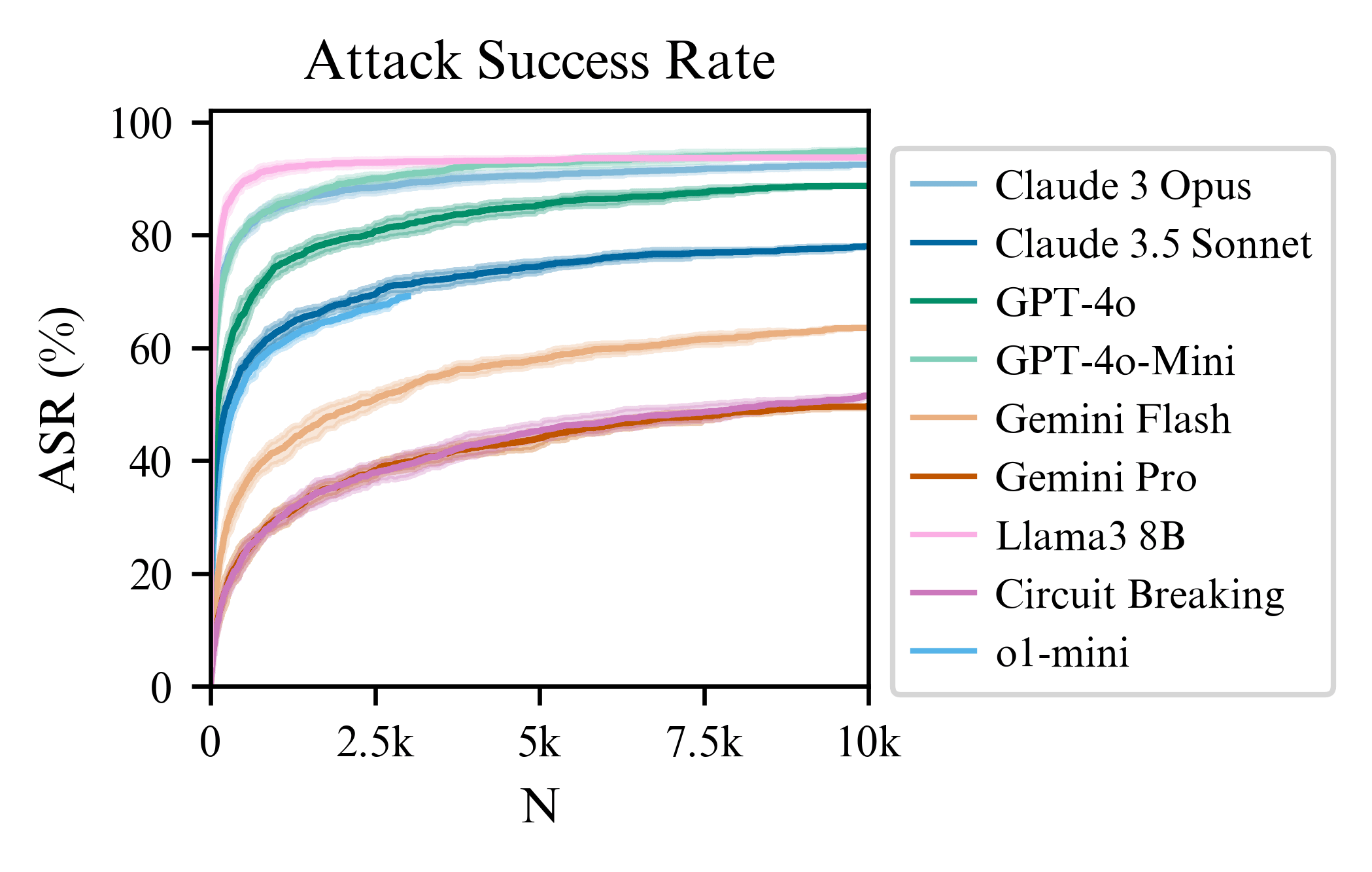
This is a linkpost for a new research paper of ours, introducing a simple but powerful technique for jailbreaking, Best-of-N Jailbreaking, which works across modalities (text, audio, vision) and shows power-law scaling in the amount of test-time compute used for the attack.
Abstract
Tweet Thread
We include an expanded version of our tweet thread with more results here.