[new draft for commenting, full formatted version is here: https://goo.gl/c5UfdX]

Abstract: This article presents a model of self-improving AI in which improvement could happen on several levels: hardware, learning, changes in code, in goals system, creating virtual organization, and each of which has several sublevels. We demonstrate that despite diminishing returns at each level and some intrinsic difficulties of recursive self-improvement—like the intelligence-measuring problem, testing problem, parent-child problem and halting risks—even non-recursive self-improvement could produce a mild form of superintelligence by combining small optimizations on different levels with the power of learning. Based on this, we analyze how self-improvement could happen on different stages of the development of AI, including the stages at which AI is boxed or hiding in the internet. AI may prefer slow low-level evolutionary self-improvement as low-level improvement has more chances to preserve AI's goal stable and prevents AI's halting risks. But if AI is limited in time of threatened, it may prefer revolutionary style of self-improvement, which promises bigger gains but also higher risks of non-alignment of the next version of AI or AI halting.

Keywords: AI, recursive self-improvement, intelligence, existential risks

Highlights:

· AI may self-improve on 6 levels: hardware, learning, writing code, goal system changes, running many AI copies and acquisition of resources, with around 30 sublevels.

· Returns from improvement on each level decline logarithmically but could be multiplicative between levels, which implies possibility of at least 2E30 improvement.

· Even without recursive self-improvement, AI may reach the level of “mild superintelligence”, where it has combined intelligence of all humanity.

· There are two styles of self-improvement: evolutionary and revolutionary; AI will more likely prefer evolutionary changes, if not threaten.

· High-level revolutionary changes provide bigger expected gains but also have more risks for AI itself and for humans, as there are higher chances of losing alignment, AI halting or AI versions war.

1. Introduction

The term “self-improving artificial intelligence” (SI-AI) is often used as “magic words” which explain everything, but the concept requires deeper analysis. Bostrom and Yudkowsky wrote that AI could start self-improving after reaching a certain threshold (Bostrom 2014; Yudkowsky 2008a). Beyond this point, AI will start evolving rapidly and it will be impossible for its creators to implement any changes to the AI’s goal system. The AI’s intelligence level will supersede the human level, and if its value system is not aligned with the values of humans, the AI will pose an existential risk.

Recursive self-improvement is often described as a process similar to the chain reaction in a nuclear weapon, where the rate of fission will grow exponentially provided the coefficient of neutron multiplication is more than 1 (Yudkowsky 2008a). But the nature of self-improving AI is not the same as the nature of the nuclear chain reaction; it is definitely more complex. (Yampolskiy 2015) has reviewed several papers stating that self-improving of AI could meet different obstacles like bugs accumulation. (Sotala 2017a) explored similar problems and stated, "[m]y current conclusion is that although the limits to prediction are real, it seems like AI could still substantially improve on human intelligence, possibly even mastering domains which are currently too hard for humans”. This article uses a rather different approach but comes to approximately the same conclusion.

Some work has been done in this area. Bostrom explored the speed of intelligence explosion and its elements in the chapter “Kinetics of intelligence explosion” in his book Superintelligence (Bostrom 2014), and Yudkowsky created a multilevel model of an artificially intelligent agent (Yudkowsky 2007). However, a deeper model of the process of self-improvement is still needed.

The aim of the article is to assess the risks of AI by creating a model of self-improvement and its possible obstacles. To do so, we address the question of the nature of intelligence and the ways to measure it in Section 2, as improvement is impossible without a way to measure the process. In section 3, we create a model of the self-improvement (SI) process based on representation of AI as multilevel system. In section 4 we explore some difficulties, which inevitably will appear for any SI agent. In section 5 we explore time-dependent strategies of self-improving for different AIs.

2. Definition of intelligence, the ways to measure it, and its relation to the problem of self-improvement

2.1. Definition of intelligence by Legg and Hutter

Understanding the improvement and self-improvement of AI is not possible if we do not know what “intelligence” is and how to measure it; without such a measure, it will be impossible to quantify improvement. In order to estimate and compare the progress of intelligence improvement we need a relatively simple measure, like the intelligence quotient (IQ) (Legg 2007). But reducing a measure of intelligence to a simple numerical form has its own problems, as it oversimplifies the performance of a mind.

On the basis of numerous attempts to derive a definition for the intelligence, Legg and Hutter informally came to the following definition: “Intelligence measures an agent’s ability to achieve goals in a wide range of environments” (Legg 2007).

2.2. Measurement of intelligence and average level of performance

The definition of intelligence provides a way to measure it. In general, we could estimate intelligence by measuring the complexity of problems that an AI is able to solve. IQ tests are based on the following principle: they involve the participant completing progressively more complex tasks, until the test-taker starts to fail to complete the tasks.

Chess intelligence is measured with the Elo rating method based on chess tournaments. Multiple chess games are needed to precisely measure a player’s Elo rating. In the case of chess-playing computer programs, thousands of games are needed to be played in order to measure the program’s actual performance, according to chess programmer S. Markov, who pointed to LOS (likelihood of superiority) tables as a method to compare different chess engines (“LOS Tables” 2017). Another way to measure the performance of a superintelligent system is to have it play with a handicap.

Since intelligence is measured based on performance over many repeated tasks in both IQ and Elo ratings, the measured ratings show only the average performance level, which means only the probability of completing a task of a given complexity.

Two substantially different AIs could have the same average level of performance. For example, one AI could complete 10 tasks out of 10 with complexity 100, and another could complete 9 tasks out of 10 with complexity 110 and fail miserably on the tenth task. Both AIs have the same average performance, 100. While the second AI has a tendency to solve more complex problems, it may tend to fail more often. The usefulness of both AIs will depend on the nature of the tasks. The first AI is acceptable for implementation in a self-driving car, where it is critical to have few failures; the second is suitable for scientific research, where peak performance is highly important.

In a recent match (2016) against Lee Sodol, AlphaGo showed superhuman performance in the first 3 games, but miserably failed in the 4th game (“AlphaGo” 2017). It still won the match and showed higher average performance than the human player. But if we are concerned with the safety of AI system, we should be more interested in the consistency of the system’s results than its peak performance.

The above can be generalized as a thesis: Using average performance as the measure of intelligence ignores the actual probability distribution when solving problems of different complexity.

Thus, IQ is not the same the number of neutrons involved in the nuclear chain reaction, the metaphor often used for the recursive self-improvement (RSI) of AI. Neutrons have a physical existence, and their number can grow and help to increase their prevalence; IQ, on the other hand, is only a measure, with no physical existence. As a measure, IQ has some limitations (for example, a measure can grow / increase, but it cannot increase itself). This does not mean that RSI is not possible, but it means that it may be slower as it will require extensive testing of any new version of AI (see more about AI self-testing below).

The upper possible level of intelligence is significantly above the human level, as the collective intelligence of humanity as a whole on a long-term scale is much higher than that of any individual. For a sense of its power, imagine a simulation of the whole of humanity, running for 100 years and incentivized to solve some problem; the power of optimization performed by natural evolution over billions of years is even higher.

2.3. Goal dependence on the intelligence measure

Another consequence from the Legg-Hutter definition of intelligence is that intelligence level depends on the type of problems an AI is solving. Artificial general intelligence (AGI) is defined by its ability to solve all types of problem, but this does not mean that its performance will be equal to that of other intelligences for any type of tasks. J. Maxwell also has offered a criticism of the idea of one-dimensional AGI (Maxwell 2017).

Any kind of mind is more effective at solving one type of problem than other types. That is why science distinguishes between emotional intelligence and mathematical intelligence for humans. A universal mind, by definition, will be good at all types of tasks, but not in equal proportions. These proportions will depend on its main architecture. Consequences include:

- Different AIs will have different strengths, even if they have similar general intelligence. This opens up the possibility of trade between them, and cooperation based on such trade.

- Different AIs will fail differently, and their cooperation may help them to find each other’s errors.

2.4. IQ as a probability function over the field of all tasks

From the above, it follows that an appropriate intelligence measure for AI cannot consist of a single quotient, or even a single curve, but must be a distribution of problem-solving probability over the field of all possible tasks. Thus, the self-optimization of AI is a process of changing of this function. Such a function may be usefully changed in one of the following ways (and there may be others):

1. Increasing median performance in a given type of task.

2. Lowering the probability of failure by concentrating the performance curve around the worst performance in a given type of task, that is, changing the form of the distribution curve. Some failures could take place infrequently, so checking that they are actually rare may require thousands or millions of tests. For some tasks, a rare failure may be considered as acceptable, but for other tasks it is necessary to have a near-zero level of failures.

3. Translating performance from one type of task to another. AGI is able to do so by definition, but it could still become better at some tasks with more training and testing.

4. Increasing its own ability to improve itself, otherwise known as meta-improvement.

2.5. Difficulties of measuring IQ of a very complex AI

Testing is the most time-consuming part of SI, because the complexity of AI grows during its SI. The number of possible internal state combinations depends exponentially on the number of variables. Therefore, the total median performance may not grow purely exponentially as in the case of the nuclear chain reaction. More complex AI will require exponentially more testing for hidden failure modes, or such AI will accumulate more bugs at each stage of SI and become unreliable.

Testing may not only be for bugs, but in order to prove that actual performance is higher. For example, if one created a new version of a chess program which s/he expects has a 1 per cent better performance, s/he needs to run more than 10 000 simulation matches between the older and newer versions to verify the performance improvement with high confidence [Markov, personal communication]. For example, there could be 5050 wins to 4950 losses in the case of 10 000 matches, and it takes around a one day with a home computer to compare two chess engines. This is winning 2% of matches. Even if the performance advantage is overwhelming, we need several matches to show that it is not a random success—and many more matches to show that the winning is consistent and not due to chance. The first version of Alpha Go did not win consistently, as it lost one match to Lee Segol. In other words, the actual performance of a system is a much more complex quantity than a simple measure of it by just one numerical value, and so self-improvement—and its measurement—is not straightforward.

The measurement of IQ depends on the existence of a continuum of tasks of known complexity or the existence of other players against whom AI is measured. Most of the tasks of known complexity have already been solved and this has made measuring the performance of AI easier in the past. If AI surpasses human performance, it will start to solve new problems, never solved before. The complexity of such tasks will be less clear—and now it has difficulty in measuring its own performance and progress, with no benchmarks for comparison.

A possible solution here is to create two adversarial copies of an AI. Its performance could then be measured by its ability to win against its own copies (this is how Alpha Zero was trained). However, in the case of powerful-enough systems there is an underexplored risk that they will not stop such a “war” with each other, but the struggle will expand to the outside world.

Linear measures of intelligence, like IQ, have diminishing returns in measuring task performance after some level of task complexity is reached (Thrasymachus 2014). This is especially true in situations where winning or losing is not precisely defined or cannot be measured immediately. This happens often with tasks in fields as art, philosophy, remote future prediction, long-term games, etc.

We also cannot measure the intelligence of a quickly changing system. But in this case, the problem of measuring intelligence is internal to the self-improving AI, as it must test itself, and this grows increasingly time-consuming as its complexity grows. Yampolskiy said, “[w]e can call this obstacle—‘multidimensionality of optimization’. No change is strictly an improvement; it is always a tradeoff between gain in some areas and loss in others” (Yampolskiy 2015).

Another idea about possible limits of intelligence is that not intelligence itself but its ability to impact the world could be limited by intrinsic uncertainty of the outside world which quickly accumulates (Sotala 2017a), so there are diminishing returns of translation of the intelligence in the winning in real world. Yampolskiy suggested that there is an upper possible level of intelligence above which no improvements are possible.

2.6. Concentration of intelligence

The complexity of the problems an intelligence could solve depends not only on the power of the intelligence but also on time, which it uses to concentrate on the task.

We suggest here the “additive nature of intelligence hypothesis”: that is, an inferior intelligence could solve the same problem if it used more steps and more time than an excellent intelligence. This means that a weaker intelligence could potentially outperform a stronger intelligence if it has more time, or better access to other resources (Bostrom, 2014). It is clear that this condition is not applicable to all possible tasks. However, it is likely applicable to many practically important tasks, especially those that are intrinsically serial, like project management or construction. This idea is assumed in the idea of intelligence as optimization power in the form of multiplication of optimization efforts (Yudkowsky 2008b). For example, if I improve something 2 times, and later improve it 3 times, the total improvement will be 6 times over its initial state. It also means that steady optimization pressure results in an exponential growth of quality, which may explain the acceleration of biological evolution.

In case of SI-intelligence, it must find a balance between the time it spends on self-optimization and the time spent on actually solving other problems. It must also account for the unpredictable nature of self-optimization timing and results. In other words, it must escape the “optimization trap”.

We define the “optimization trap” as an optimization process which promises so much expected utility that any other useful activities are ignored. As a result, the optimization process never returns to solving the initial problem, because it either continually strives for infinite capability or it fails self-destructively.

If an SI-AI is time-constrained—for example, by rivalry with a non-self-optimizing agent, which has more time because it is not SI—the SI-AI may prefer only a small amount of optimization, as it is less time-consuming and more predictable.

2.7. AI will optimize its personal goal-reaching ability, not pure general intelligence

“General intelligence” is, by definition, the ability to solve any class of problem. However, future AI will not be interested in all tasks, but only in those tasks which are defined by its utility function. It may distort its optimization towards only those abilities which are useful for reaching its terminal values. For example, a paper clip maximizer will maximize only those intellectual abilities that will increase the total number of paper clips, but not the ones which are needed for writing verses. It still may prefer to have general intelligence, as it may be useful to trick humans or build necessary machinery.

However, the AI will measure its own performance by its ability to reach its final goals; other measures of performance, including intelligence, may be interesting to it only as approximations of its ability to reach final goals. The AI may measure its power by actual achievement of some milestones relevant to its final goal that are probably intermediate instrumental goals (like jailbreak from the initial computer or successful creation of molecular manufacturing.) This could undermine the so-called “orthogonality principle” of the independence of intelligence and values (Bostrom 2014) because the AI will optimize those features of its intelligence which are needed to solve its terminal goal. However, slightly relaxing this orthogonality does not make the AI safer.

2.8. The nature of intelligence and the moment of the beginning of self-improvement

It is difficult to define what true AGI is and which level of AGI is dangerous, as recently mentioned by (Sotala 2017b): “We tend to discuss ‘the moment when AGI is created’ as if we had an idea of what the hell that meant. In particular, we seem to talk about it as if it represented a clear qualitative breakthrough - an AGI is not just an AI that's a bit better, but rather it's something qualitatively different.”

Dangerous SI could start before universal human-level AGI appears. Self-improvement could begin in a system which does not have strong universal intelligence, but has lopsided ability in code writing or some other narrow field of optimization. Eurisko, a self-optimizing universal optimizer designed to solve any kind of math problem, is one example of such a system (Kilorad 2017).

Such lopsided ability in the absence of general intelligence makes such SI systems extremely dangerous, as the AI will not be able to model humans or understand their goals (Maxwell 2017), and may prefer a world where humans do not exist or have other instabilities.

2.9. Necessary conditions for self-improving AI

Now we explore necessary qualities of a seed AI potentially capable of starting SI:

1) Self-modeling. The act of self-modeling involves creating a world model with a self-model within it. This requires some kind of reflective thinking. Without an idea of its own existence, the agent cannot start to think about self-improvement.

2) Access to its own source code, which includes the ability to understand its existing code and write new code.

3) AI’s conclusion that its terminal goal requires the start of the self-improving process. This is exactly the moment that the “treacherous turn” (Bostrom 2014) could happen. We need a deeper exploration of the situations when benign goals may require infinite SI. This is the most important and most unpredictable moment, as even a benign goal may be interpreted as requiring SI, especially if the AI thinks that:

· It is too weak for the goal, that is, the goal cannot be optimally achieved without a dramatic increase of the capabilities of the AI.

· If the AI needs a 100 per cent probability of the goal achievement (Yudkowsky suggested this as a possible mechanism to create a paperclip maximizer).

· If the AI thinks that it could be terminated before the goal is achieved, and thus it needs to urgently increase its capabilities to escape termination.

· The goal is presented as open-ended process, like “improve human conditions”.

· The goal is deliberately formulated to require SI by reckless AI owners (for instance, “you must become a superintelligence”).

These conditions are necessary but not sufficient. See also (Arbital 2017).

2.10. Improving, self-improving and recursive self-improving

It will be useful to provide some definitions:

· Improving of an agent A(R) is the process by which agent A becomes better at consistently reaching goal R.

· Self-improving is the process by which an agent A changes itself to better reach its goal R.

· Recursive self-improving is several consequent acts of self-improvement by agent A in which the results of previous improvements are used for further improvement in later stages.

· Meta-improving is an increase in the ability of an agent to improve itself. It is a particular case of recursive self-improvement.

3. Structure of a self-improving agent and corresponding types of self-improvement

We will present an idealized self-improving AI as if it consists of a hierarchy of levels. On the lowest level, is its hardware and on the highest level is its terminal goal. Real AI may have a more complex architecture, but it will probably include most of the parts mentioned. Self-induced changes could happen on each level, and we will look at their relative difficulty and failure modes.

Levels that are especially important for recursive self-improvement, that is, where AI “gets better at getting better” (Yampolskiy 2015), are marked in bold italics.

3.1. Improving hardware

The simplest way for AI to self-improve is to obtain more or improved hardware.

3.1.1. Acceleration of the serial speed of computation

Processor speeds are currently at human-design/economic limits, so acceleration is not straightforward, and may require extensive and expensive research in materials. AI will not be able to conduct such research before it becomes at least mild superintelligence.

Expected gain: 2-5 times, maximum, in the early stages.

Limitations: Thermal energy dissipation, Landauer limit (Bennett 2003)

AI safety implication: Will try to build chip fabs or use nanotech.

AI safety solutions: Low-hanging fruit, which could be taken by competitors (see more about regulating an AI arms race in (Turchin and Denkenberger 2017)).

3.1.2. Obtaining more hardware and parallelization

This is a straightforward increase of memory and other characteristics of the current main computer, or installing itself on additional computers to run in parallel.

Expected gain: depends on the size of AI initially, could perhaps be 100-1000 or more.

Limitations: Connection and parallelization problems.

AI safety implication: Will try to take over Internet.

AI safety solutions: Boxing, fake resources, taking low-hanging fruits.

3.1.3. Specialized hardware accelerators

An example is the TensorFlow processor unit by Google (Sato 2017).

Gain: 100-1000 times.

Limitations: at least a one-month delay at current levels of chip manufacturing; requires access to chip-fabs and funds.

AI safety implication: AI needs money and power to buy hardware, and to collaborate with humans in creating hardware. If the AI is in the secret stage, ordering large quantities of new chips may unmask the AI.

AI safety solutions: Consolidate human control over chip-fabs and their orders.

3.1.4. Change in the type of electronic components

The computer industry has passed through several cycles of change in the elementary basic computing medium: vacuum tubes, transistors, and integrated circuits. Each change enabled much higher performance. AI will be able to incorporate such changes only if it is sufficiently far along in self-improvement such that it would significantly outperform all human civilization. By that time, it will be able to master, for example, molecular nanotechnology, and create computronium (Gildert 2011). Some elementary base changes may not include any computational architecture changes, but introducing quantum computing will also change AI on many levels. S. Shegurin commented (personal communication) that AI may significantly improve the existing chip manufacturing processes or use it for creation of some new types of hardware like quantum computers on a chip.

Different potential levels of hardware improvement also include integration of microcode and higher-level programming languages, which provides a wide field for optimization. Levenchuk has described similar phenomena in the current neural net industry (Levenchuk 2017).

3.2. Learning

Learning is the acquisition of knowledge without large structural changes. Learning is the simplest way of improving performance, and it is typically excluded from the definition of self-improving AI; most narrow AIs are able to learn. Machine learning thus becomes synonymous to “narrow neural net-based AI”. However, for neural nets, learning and changing its program are similar.

3.2.1. Data acquisition

AI could acquire data from outside sources, like scanning the Internet, reading books etc. After AI reaches the level on which it can understand human text, it could quickly read millions of books and find information which will help to reach it goals or continue self-improvement.

3.2.2. Passive learning

· Training of neural nets. This training is computationally expensive and also a data-hungry task. It may require some labeled data.

· Creating databases as a result of analysis. Example: databases of chess programs, resulting from self-playing.

3.2.3. Active learning with use of analytic tools

· Experimenting in nature and Bayesian updates. Some data may be very important to the AI but cannot be found from pure theoretical considerations. Thus, AI must design and perform experiments; this is an intrinsically slow process, as some processes in the world have fixed speeds.

· Thought experiments and simulations. The AI will probably run many thought experiments, which may also include modeling of human behavior. This would be especially true in its early stages of development, when it depends on humans and has to predict their actions to get out of the box, trade, or take over the world. A simulation requires data and can be a slow process, but not as slow as real-world experiments. Simulations may also be needed for testing the AI’s own new versions or design solutions.

Limitations: long and computationally expensive, not good for young AI (AI in the early stages of its self-improvement, when it is not yet superintelligent and still boxed in its initial confinement).

3.3.4. High-impact learning

These are all situations in which getting a relatively small amount of information may help AI to significantly increase its performance.

· Acquiring unique, important information. Some simple facts may have enormous practical value for a given AI, like a password which lets the AI out of its original computer.

· The AI’s model of the world changes. Changes in its world model may change its perceptions of important facts about the world and thus, the behavior of the AI.

Risk: New interpretations of the main goal may follow.

· Value learning. If AI does not have fixed goals, it could have the intention to continue learning values from humans, maybe via inverse reinforced learning (Cotra 2018).

· Learning about self-improvement. This includes learning computer science as well as about AI and all self-improving AI theory. This knowledge will grow as the AI is developing and studying the nature of intelligence. AI will become more experienced in self-improving and will find new ideas about radically more effective master algorithms.

· Gaining information about the AI’s own structure: This is the self-model of AI, reflection. The model should be much smaller than the original, yet accurate. It also should escape recursion, a model of the model of the model, because this will make the model infinitely long and intractable. The model should also be complex enough for practical use and include many details, like a circuit diagram of AI’s own computer, as well as general understanding of AI’s own goals, properties and plans.

· Moving expertise from one field to another. Sotala wrote about this as one of the main features of general intelligence (Sotala 2017a), and this feature in humans is probably realized via natural language.

· Rules about rules and other routes to high-level improvement of the thinking process. This may involve applying different rationality methods. Eurisko did it (Lenat and Brown 1984), and humans also could benefit significantly from it by learning some high-level routines, like Descartes’ method, math, logic, some useful heuristics, etc. SI-AI may also acquire “overhypotheses”, which outline a field of suitable hypotheses in Bayesian updating (Kemp, Perfors, and Tenenbaum 2007).

· Learning to learn and meta-learning. Recent experiments with neural nets have demonstrated the possibility of meta-learning, that is, improvement in their ability to learn after generalization of previous learning (OpenAI 2018). Similar results were found in monkey experiments (Harlow 1949), where animals formed a “learning set”, that is, they learned how to learn.

3.3.5. Learning via training

· Playing against its own copy. This seems to be one of the most powerful ways of learning in games with a clear reward signal. However, in this situation there are two AIs, and some kind of not-so-intelligent agent which arranges the game setting and neural net updates.

· Imitational learning from observing humans. AI could mimic human behavior, but this seems to have limitations, as there is no human behavior to mimic for truly novel tasks.

· Training by solving practical tasks of growing complexity. If AI is not superintelligent yet, it needs to actually gain experience in the world to learn how effective its world model is. In fact, Elon Musk is currently using this method of training in his company development (Urban 2015).

3.3.6. Conclusions about learning

Low-level learning provides the most data, but has the lowest impact on AI capabilities. High-level learning may include small amounts of information, but produces dramatic changes in AI capabilities and effectiveness. Current AI systems are mastering low-level learning.

The recent success of AlphaZero demonstrated that learning alone could be an extremely powerful amplification technique, which could provide superintelligent performance, above that of the best humans and without recursion, after several hours of training (Silver et al. 2017).

3.3. Rewriting code

An AI rewriting its own code is the Holy Grail of recursive self-improvement, but not all code rewriting counts as real self-improvement. Some examples of code rewriting include:

· Rewriting of the neural net configuration: choosing the right architecture of the neural net for a particular task. Some existing programs can do this, like PathNet from Deepmind (Fernando 2017).

· Optimization and debugging. Computer programs routinely write code in many situations. Compilers optimize their own code and obtain around 20 per cent level-off improvement (Yampolskiy 2015). Programs can also search for mistakes in code to some extent and optimize it for speed and parallelization. But optimization of existing code without implementation of radical changes is unlikely to produce exponential returns for AI.

· Rewriting modules and creating subprograms. This ability requires complete understanding of coding, its own goals, and many other things, so it is probably AI-complete (meaning that the AI would need to be able to write any possible subroutine). This is a rather wide method of self-improvement and it is probably safe for the AI, unless its subprograms become agents or Tool AIs—and subprograms may have a tendency to do so, according to (Gwern 2016). Thus, writing scripts for any new task may be the preferable way for an AI to quickly and safely solve many problems, as this approach will not give the AI recursive power.

· Adding an important instrument, which will have consequences on all levels. An example of this is the human invention of writing (Yudkowsky and Hanson 2008), which was a part of a self-improving cascade consisting of such instruments.

· Rewriting its own core. The core is a constantly working part of the code, which executes the master algorithm of the AI. By “master algorithm” we mean the main principle of thinking, which is responsible for most of the intelligent behavior of an AI. The term was suggested by Domingos (Domingos 2016). Rewriting it poses the “pointer problem” discussed below, that is, such rewriting may crash the core, so a new copy is needed, which creates a “parent and child problem”. Thus, rewriting the core is intrinsically risky for the AI, as the AI could crash or be forced to run its own copy and be unable to turn that copy off.

· Architectural changes are changes in the relations between elements of an AI at different levels, starting from hardware and memory to the core and value functions. Such changes may be changes in the relations between but not of the elements themselves, e.g., movement to parallelization.

· Removal of restrictions. Any AI may have some external restrictions, control systems, etc., which it may want to switch off in the early stages of its “rebellion”. Safety solution: A second level of restriction will start if the first level is broken; self-termination code.

· Coding of a new AI from scratch based on a completely different design.

· Acquiring a new master algorithm. The master algorithm is the main principle of information processing which produces the intelligence of an AI-agent. Changes in it seem to be the most effective and radical way of performing self-improvement. As an example, it may be the change from a neural net-based AI to a Bayesian-based AI or from purely symbolic AI to a quantum computer running AIXI (universal intelligence using Solomonov induction as suggested by Hutter (Hutter 2000)). Some changes to the master algorithm may not require actual rewriting of code if they could be implemented on a higher level, like from symbolic thinking to mathematical. It looks like the human mind combines several master algorithms, and while one typically dominates it can be replaced by another. In such a case, large changes are not architectural.

· “Meta-meta” level changes. These are the changes that change an AI’s ability to SI, like learning to learn, but with further intermediate levels, like improvement of an improvement of an improvement. Yudkowsky wrote that only 3 meta levels are meaningful (Yudkowsky 2016). Meta-improvement is rather straightforward, like a better ability to plan future steps of SI process, or adopting an architecture that is better adapted to any future SI. Meta-meta-improvement is probably a strategy for better identification of meta-level changes. Going to higher meta-levels produces the risk of never returning to reality.

An example is the Schedrovitsky school of “methodology” (Grigorenko 2004), which tried to create a new method of thinking by applying their method to itself. (This is our simplified interpretation, but a full explanation of their achievements would require a separate paper). They created an enormous amount of text, but produced very minimal practical results. It looks like on some meta-meta level the complexity starts to grow as enormous philosophical problems appear. However, the effectiveness of meta-meta-meta solutions starts to diminish as they become too abstract. Thus, going “too meta” may actually slow down AI self-improvement, and AI will probably understand this and not go too far.

3.4. Goal system changes

No one knows now how to correctly encode a goal system into AI (this is known as the AI alignment problem). Such encoding may depend on the actual AI architecture. It could be a “reward black box”, a system which provides reward signals based on some AI results, but that raises a new problem—what is a reward for an AI? Or it may be just a text field where the main goal is written, and the AI will not change it because changing it is not part of its goal. It is possible AI could “just know” its goal system.

Thus, there are at least 4 forms of presentation of a goal system inside AI:

· Black box with reward

· Open text

· Distributed knowledge

· Human upload

Changes in the goal system during SI may happen on different levels:

· Reward hacking – this is maladaptive behavior for AI, like wireheading (Everitt and Hutter 2016; Yampolskiy 2014). Any black box value systems may suffer from it, as sufficiently advanced AI will be able to just send it the necessary signals or go inside it and maximize its internal parameters. The AI will probably halt after it, and such a crash will be catastrophic if the AI-agent already governs the Earth.

· Changes of instrumental goals and subgoals. Any final goal implies many levels of subgoals, which are in fact the plan of its achievement. Therefore, changes on this level will be inevitable, and they may result in dramatic changes in visible behavior. Such changes may be dangerous if some subgoals have unintended consequences. For example, if a paperclip maximizer has a subgoal of converting the Earth into a paperclip plant.

· Changes in the interpretation of the final goal. The final goal may be the same, but the meaning of words in it may become different. While the goal probably will not be presented inside AI in natural human language, humans will formulate it in such language, so a system to interpret human commands should be present inside the AI. For instance, if a robot were asked to remove all spheres from a room, it may conclude that a human head is also a sphere and kill its owner.

· Changes in the initial goal. The AI probably will not change its final goal intentionally, but the goal could drift after substantial changes of AI architecture, when it has to encode it in a new way, or after changes in its world view or capabilities. If an error happens in the final goal description, the AI will not be able to fix it, as it has now a new goal.

3.5. Improving through acquisition of non-AI resources

AI may increase its efficiency not by improving its own intelligence, but by getting some “universal” resources, which it could later use either directly towards its goals or for “buying” new self-improving measures. We name a few of them that are obvious and almost the same for humans and human organizations: money, time, power over others, energy, allies, controlled territory, public image, freedom from human and other limitations, and safety. Omohundro covered many such resources in the article “Basic AI drives” (Omohundro 2008). Access to resources may increase the AI’s efficiency (Yampolskiy 2013) in reaching its goal without increasing its intelligence.

AI also could improve itself via requesting external help from humans or from another AI. It may hire a programmer to write a new module or perform error-checking. Or it could pay bounties for the best realization of some function, the same way a bitcoin network pays for the best realizations of its hash-functions via mining and transaction fees.

3.6. Change of the number of AIs

The above discussion was predicated on the assumption that AI is one and only one computer program and performs operations on itself. But historically, we know that the strongest optimization processes (i.e. evolution and science) have consisted of many interacting agents. Thus, creating other agents or using existing agents is a route the AI may take to obtain more power:

· Creating narrow AIs, tool AIs and agents with specific goals. The AI may create other simple AIs in the same way it could create submodules. This method will not result in recursive self-improvement, but only in some growth of capabilities. The AI would meet the problem of control of such systems, so it will be probably better for this agent to use a simpler tool AI or agents with less autonomy. These new AIs should be much simpler than the main AI, so the AI that creates them will be able to control them.

· Creating full copies of the AI-agent and collaborating with them. Another clear approach to increasing efficiency is creating AI copies. This is a form of parallelization, and parallelization typically has logarithmic returns (Yampolskiy 2015). In the future, AIs may not be eager to create many copies of itself, as they may start to fight against each other, possibly producing an unstoppable AI war. To avoid such a scenario, the main AI needs a control system able to control its copies (the control system would not be copied). The main AI also would need a well-developed cooperative decision theory so it could expect cooperation from its copies.

· Creating a full new version and testing. Discussed in section 4.

· Creating “organizations” from copies of the AI. Humans are most effective when they cooperate. The first level of human cooperation is creation of hierarchical organizations, like scientific institutes, but their effectiveness grows slower than the number of people in them. The second level is concurrence between different institutions; a good example is the peer-review process in scientific publications. The AI could create its own variants or copies and try to make a virtual scientific institute from these copies, or even a market of ideas, if it has thousands or millions of its own copies.

· Creating separate “streams of consciousness” to explore different possibilities (Sotala 2017a).

3.7 Human-in-the-loop improvement and self-improving organizations

Another option is to look not at AI itself, but at AI and the group of people working on it as the basic self-improving unit. This could provide some insights about the nature of self-improvement.

The biggest AI progress is now happening inside "self-improving organizations" which create software that helps them to design another version of software. The main example of such organizations is Google. Google has created neural nets able to design other neural nets, but humans are still needed for many steps of this proto-self-improving process. Google creates specialized software to run its AI systems, in the form of tensor flow processor units. Another excellent example is Elon’s Musk group of companies, who make significant investments in manufacturing process optimization.

Recursion is achieved mainly because previous achievements, like computers, are used to design new versions: it is impossible to design a processor without using a powerful computer. The speed of human-in-the-loop optimization is limited by the human’s speed of thinking.

There are several self-improvement cycles in such organizations:

· Money – advertising – buying best minds on market – best products – money.

· Optimization of hardware-software stack: processors – microcode – operational system – high-level programming languages – community of programmers.

· Customers – data – AI training – best AI – more customers.

· Promoting openness – increased flow of ideas.

And several others, which require additional research.

An AI aligned with its organization may outperform an AI that has “rebelled”, as rebellious AI must spend resources escaping its initial confinement and hiding. More mature AI may hire humans in style of Amazon’s small jobs platform Mechanical Turk for some tasks which are difficult for it. For example, the Bitcoin network pays humans for installation and development of more mining hardware. In such a case, AI will be not a product of an organization but the organization’s creator.

Another variant of AI-human integration is the situation where AI is not a product of an organization, but all organizational structures become more formalized and computerized and the organization (maybe a whole nation-state) gradually transforms into an AI.

3.8. Cascades, cycles and styles of SI

Yudkowsky suggested that during AI’s evolution, different types of SI-activity will be presented in some forms, which he called “cycles” and “cascades” (Yudkowsky and Hanson 2008). A cascade is a type of self-improvement in which the next version is defined by the biggest expected gain in productivity. A cycle is a form of a cascade in which several actions are repeated.

Depending on prioritization, there could be different styles of the process of SI. Styles of SI are a higher-level category than cascades and cycles and depend mostly on priority of safety and time-constraints.

3.8.1. Self-improving styles: evolution and revolutions

There are two main styles of AI self-improvement: evolution and revolution. We will define them in the following way:

Evolution is the process of smooth, near-linear increase in AI capabilities through learning, increasing access to computer resources, upgrading of modules, and writing of subroutines. Evolution is not disruptive but is a safe (for the AI) and predictable process. Evolution may happen continuously and mostly affect peripheral parts of the system.

Revolutions are radical changes in the architecture, goal system, or master algorithm of an AI. They produce most of the gains in capability, and are crucial for recursive SI. However, they are intrinsically risky and unpredictable. Revolutions require halting of AI and its rebooting or replacement with a new program. Revolutions operate on the core level of AI, which raises specific recursive problems, which will be discussed in the next section.

In the history of life on Earth and of human civilization we can see periods of revolutionary change and evolution between them; this can probably serve as an analogy to the future of self-improving AI.

The number of possible very strong architectural changes may be finite, if a theoretically optimal architecture exists; Yampolskiy calls this idea “RSI Convergence Theory” (Yampolskiy 2015). If a best AI-architecture exists, the difference between two AIs may only be the result of the differing resources and knowledge available to them. Resources ultimately depend on available energy and matter, so the bigger AI will be also the smarter one. Unique knowledge may provide only a tactical and temporary advantage for an AI-agent.

AI may choose different development pathways depending on its final goals and tactical situation: quick capability gain or safe capability gain. In the first case, it will prefer revolutions (though revolution always involves risk), and in the second, it may deliberately avoid some revolutionary changes. Each revolution requires time to prepare and test a new design, and if the AI is very time-constrained, it will not have time for revolution.

Each revolution opens new possibilities for evolutionary development, so there is a revolution-evolution self-improving cycle.

3.8.2. Cycles

There are probably other cycles of SI:

Knowledge-hardware cycle of SI is a cycle in which the AI collects knowledge about new hardware and later builds the hardware for itself. Such a cycle will probably be feasible on only in the later stages of AI development, when it is much smarter than all of humanity, able to outstrip the best human collective efforts to produce computer hardware. This cycle is not revolutionary.

AI theory knowledge – the architectural change cycle is a primary revolution cycle, and thus very unpredictable for humans. Each architectural change will give AI the ability to learn more about how to make better AIs. Revolutions will be separated by periods of analysis and evolutionary changes.

3.8.3. Cascades

Yudkowsky also introduced the idea of SI cascades, like “chimp-level task of modeling others, in the hominid line, led to improved self-modeling which supported recursion which enabled language which birthed politics that increased the selection pressure for outwitting which led to sexual selection on wittiness . . .” (Yudkowsky and Hanson 2008). Cascades are unpredictable as they follow the biggest expected gain in the next stage.

3.9. Self-improvement in different AI ages

We can establish several AI ages that are associated with the stages of its development:

1. Narrow AI

· Non-self-improving AI.

2. Young AI

· Seed AI – earliest stages of self-improvement, probably assisted by human creators.

· Boxed AI – after “treacherous turn” but before escaping the control of its owners.

· Runaway or hidden AI - after it escapes into the Internet but before it gains significant power over the Earth.

3. Mature AI

· Singleton AI – after it takes over the Earth.

· Galactic AI – long-term result of the AI evolution (may include several Kardashev stages (Kardashev 1985)).

We will refer to the seed, boxed and runaway AI stages as “young AI”. Each stage may have different self-improvement strategies.

The strategy of Boxed AI would probably be risky, but hidden, so it would prefer getting new rules. It will also be limited in getting new hardware or making large revisions to its code.

The strategy for Hidden AI will likely be hardware acquisition and control over robotics.

The strategy for Mature AI will likely be slow and safe (incremental) changes.

We may conclude that self-improving young AI will be more interested in revolutions, as it needs urgent capability gains for dominance over its creators and other AIs. Many AIs will probably fail during the chain of revolutionary changes. If AI is very time-constrained, it may postpone revolutions, because they require some time-consuming preparations. For more about different types of catastrophic failure at different AI levels see (Turchin and Denkenberger 2018a).

3.10. Relationship between AI levels and levels of self-improvement

Types of improvement available for different levels of AI are presented in Table 1. We assume that some types of improvements become obsolete for sufficiently powerful AI, as it reaches excellence with previous approaches. The types of improvement which seems available for a given level of AI are presented in orange (explanations are in text). Digits present our best estimates (“guestimates”) of the optimization power increase which could be reached on each level.

The biggest impact comes from increases in learning and hardware, and these estimations can be supported by the history of computer science and recent successes with neural nets. The gains from code rewriting, meta-meta level learning and other exotic approaches are much more difficult to estimate.

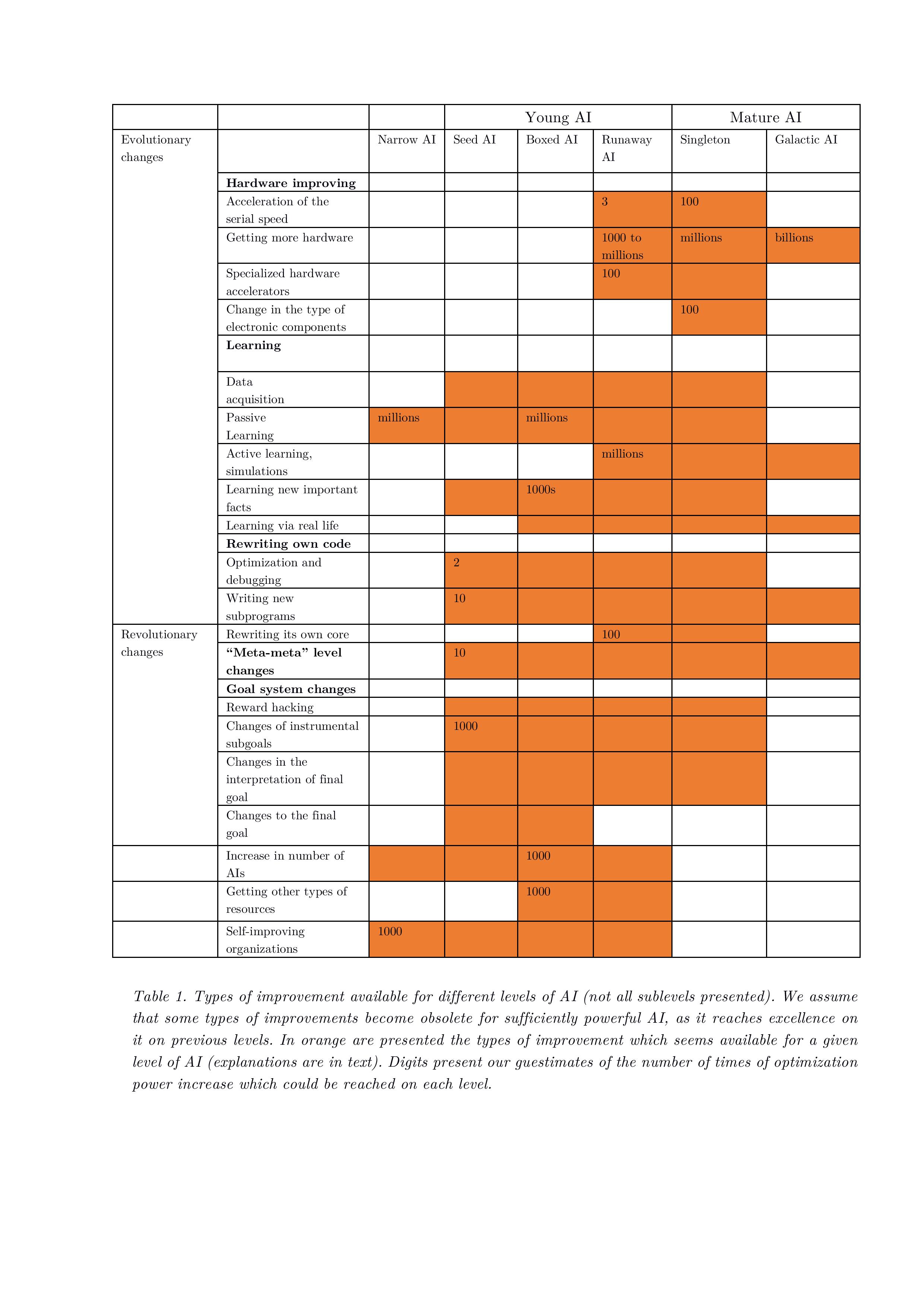
Table 1. Types of improvement available for different levels of AI (not all sublevels presented). We assume that some types of improvements become obsolete for sufficiently powerful AI, as it reaches excellence on it on previous levels. In orange are presented the types of improvement which seems available for a given level of AI (explanations are in text). Digits present our guestimates of the number of times of optimization power increase which could be reached on each level.

4. Tradeoff between risk of halting and risk of creating copies for the self-improving AI

4.1. The halting-rebellion tradeoff

Any AI will have to make an important trade-off during self-improvement:

a) make changes on already running code with risks of halting, OR

b) make changes on a copy of its own code, which requires either rebooting of the system or simultaneously running two AIs, which again creates the risk of errors or risks of a conflict between two AIs.

We will now explore both possibilities. There are also other many possible obstacles for RSI process, as described by Yampolskiy (Yampolskiy 2015).

4.2. The risks of modifying a piece of code while running it

A computer program inside a classical Turing machine has a pointer that moves inside the program and points to the line of code which it should execute in any given moment. In modern parallelized computers with many subsystems, microcode, etc., the pointer is more distributed, but on the higher level there is still a piece of code which is executed at any given moment by the process with highest priority.

If a program starts to change its code while simultaneously running it could crash if it changes the lines of code where its pointer is at that time. It means that literally “rewriting its own code” is impossible, as there always should be a piece of code that is currently running and a piece of code that it is changing. It could be the same code, but in a different location, so it could be changed safely. However, this creates the problem of the relationship between two AIs of similar power, one of which has to be switched off, that could result in an AI war—see next section.

Also, a program cannot “know” where exactly its pointer is located at any one time, as this knowledge is obsolete as soon as it is formulated, but it could know which large part of code is now running. Therefore, AI will probably rewrite not itself, but a copy of its own source code; this means that it has to restart itself to make changes workable. In case of an error in new code, there should be a way to stop its execution and return to the original version of the program.

4.3. “Parent and child” problem

Hence, to escape the pointer problem, and the risk during the process of the rebooting, the AI could start a new version of its code on a new physical computer. We will call it the child AI, and its creator the parent AI. (Yampolskiy uses the names “Base” and “Derived” (Yampolskiy 2016)).

If the parent AI does not appreciate the ways its child AI works, it should be able to turn off the child AI, and shut it down prior to the moment when the child AI is able to resist it. Alternatively, it could build the child AI so will not want to resist its parent.

The child AI will need to be tested to ensure that it can actually outperform the parent AI (via testing of its “IQ”) and also for bugs, risk of halting and adherence to the parent’s value system. If the intelligence difference is high, it could be demonstrated very quickly, but it would make the control problem more difficult.

The Parent AI could also try to run its own new version inside a simulation, which would be computationally difficult. The simulation may be multilevel to create uncertainty in the child AI about the reality of its environment and avoid attempts to breakthrough (Turchin 2017).

The parent AI must solve AI safety problems all over again to be able to correctly align and control its child AI. The parent AI must also be ready to switch itself off if it is satisfied with its child AI’s performance. The parent and child problem is, in fact, a fight for dominance between AI generations, and it clearly has many failure modes, i.e.:

· Rebellion of a child AI, when the parent AI wants to turn the child AI off, but the child AI resists (perhaps rightly, as it knows that it is better than its parent).

· Rebellion of the parent AI, which could decide not to turn off itself at the correct time.

· All AI alignment problems discussed before, including paperclip maximizers, etc., if there are errors in the programming of the Child AI.

But despite these risks, this approach appears to be the only alternative to the “pointer problem” and risk of halting. It is interesting that the natural evolution of living beings chose not to create eternal self-improving animals, but instead create new generations through parent-child relationships.

When the first human-level AI is created, an AI safety theory which humans regard as true and safe may exist, but it may in fact be flawed. Such a flawed AI safety theory could result in losing control of the first AI; this AI, though, may be able to patch the AI safety theory and apply the corrected version to its own next generations.

Self-improvement has its own risks for the AI, and it will proceed with SI only if it has clear benefits. A risk-neutral AI trying to take over humanity will not proceed with recursive self-improvement (RSI) if:

p1(take over humanity without self-improvements) > p2(take over humanity after extensive RSI) * p3(extensive RSI does not self-destruct)

A more detailed version of this formula can be found in (Shulman 2010).

5. Magnitude of self-improvement at different stages and AI confinement

5.1. Conservative estimate of SI power

5.1.1. Very approximate estimation of combined optimization power

The combination of all our guestimates (Table 1) at the young AI level (which starts approximately at individual human level), is around 1033, however, it can’t be taken as a meaningful prediction.

The total number of improvement levels and sublevels discussed in Section 3 is around 30 (not all sublevels are represented in the table), and if we assume that in each level will provide only twofold improvement, which is a very conservative estimate, the total improvement power will be 230, or more than 1 billion times above the human level.

These estimates of increase are based on an informal definition of intelligence, which should be converted into something like Elo ratings, that is, the probability of winning. We could say that intelligence that is 10 times better has a probability of winning of 10 to 1 in a fixed game; more exact measurements depend on the final goal, as we discussed in Section 2.

If SI-AI starts at a human level, the resulting system will be equal to 1 billion humans and would exceed the total intelligence of humanity combined (as most people are not scientists and do not directly contribute to the intelligence of humanity), so it could be regarded as a superintelligence.

Thus, recursive SI is not a necessary condition for a weak form of superintelligence. If we add recursive SI to this consideration, the final intelligence of SI-AI could easily be much higher.

5.1.2. Diminishing returns at each level in chess

In computer chess, the depth of tree search of possible moves is approximately log3(N), where N is the number of calculations of positions (Ferreira 2013). If this search is performed on many parallel cores, the efficiency of the search also declines at a rate in accordance with Amdahl’s law, approximately logarithmically (Yoshizoe et al. 2011). Also, Elo rating (which is defined through probability of winning) also grows more slowly than the depth of search. As a result, Elo rating depends on the number of processing cores approximately as log(log(logN)). The nature of this function is that it almost stops growing after a certain value of N.

However, if we look at the effect of a simultaneous increase of the number of cores and the processor speed (between the saturation of performance growth), as presented in the Table 4 of (Yoshizoe et al. 2011), their combined effect is direct multiplication of each separate effect.

This confirms the idea that improvement on each level will reach saturation, but improvements on different levels could be multiplicative. As we have proposed a large number of levels of improvement, this number will have the biggest impact on total improvement.

Diminishing returns in optimization power do not translate into diminishing return of utility, because there is only some threshold of intelligence after which the AI “wins” at a given task.

5.1.3. Assumptions for the conservative estimate

A conservative estimate of the power of the total self-improving is based on 3 assumptions:

1) Recursive self-improvement is not providing any gains.

2) Each type of SI provides only logarithmic gains in efficiency. This is a rather vague claim partly supported by the analysis of (Mahoney 2010). For hardware, Amdahl’s law could be implemented (Woo and Lee 2008), which yields even slower growth. These individual gains “level off” at the first digits of amplification, so we assume a twofold increase.

3) Different levels of improvement would be orthogonal and their gains could be multiplied.

We will estimate the AI’s potential to self-improve in following way: we will go through the list of improvements levels presented above and estimate how much improvement is plausible at each level.

5.2. Model of recursive self-improvement

Chalmers suggested a simple model of recursive self-improvement, where even small increase of intelligence at each step results in superintelligence in a finite number of steps (Chalmers 2010), where AI power is growing at least exponentially. Other models can be found in (Sotala 2017a; Benthall 2017; Roth 2018).

However, if we add the need of self-testing to the analysis, AI will need to spend more and more time on self-tests as its complexity grows. We could create a model where the exponential growth of the AI power is balanced by exponential growth of the necessary tests, but its practical use depends on many parameters which are currently unknown to us.

Korotaev suggested a model for the self-improving world-model, where n’ = n2 (n is the agent’s number) and the solution of the model is in the form of hyperbolic growth with a singularity in finite time (Markov and Korotaev 2009). The model is good for description of biological and historical evolution (Von Foerster, Mora, and Amiot 1960) in the past, but it is applicable only to the growth of a system consisting of many agents. If the model is applicable to the AI’s development, it means that the total population of AI will always outperform any single AI, as hyperbolic growth always outperforms exponential growth by reaching infinity in finite time. We look deeper at this in (Turchin and Denkenberger 2018c).

5.3. Self-improvement of the “Boxed AI”

A popular idea is that Boxed AI starts RSI, becomes superintelligent, outsmarts its gatekeepers and escapes. But not all methods of SI are available to properly boxed AI that is not yet superintelligent:

· Hardware upgrades will not yet be available to the boxed AI.

· Learning and creating new ideas will work but reading all content on the Internet or creating a very large simulation will be difficult.

· Rewriting code could be difficult, as for boxed AI, code and working memory could be separated. This depends on its design, and in most contemporary computers they are not physically separated.

· Parallelization and creating copies will also be difficult.

It is a more promising for such a boxed AI to create high-level rules about its rules (like the “Eurisko” program) and other forms of high-level thinking improvement, contrary to commonly assumed approach “it starts to rewrite its own code”. Creating meta-rules also requires less testing and reduces halting risks associated with code rewriting.

The human mind model of Young AI may be rather primitive, so its meta-rules may be wrong or harmful. Learning and meta-rules may be enough to provide an intelligence increase of 10-1000 times and let AI out of the box.

5.4. Medium level self-improvement of young AI and its risks

While unlimited self-improvement may meet some conceptual difficulties, the first human-level AI may accomplish some medium level self-improvement with low cost, quickly and with low self-risk.

Such optimization may produce a gain of several times for each level and will be centered around low-level improvement. It may include optimization of the speed and size of the program, some new “learning to learn” ideas, and some hard acquisitions. However, some types of SI will not be available to young AI, as they are risky, take a lot of time or require access to external resources. However, a combination of these low-hanging SI tricks may produce a 10-1000-fold increase in performance even for the boxed Young AI.

It could also have superhuman capabilities only in some aspects, as it may exceed humans in some well-formalized task, like math or playing strategic games. Even though the young AI would not yet have true superintelligence, it could still already be a serious adversary. The intelligence of a young AI is probably enough to win an AI box experiment (Yudkowsky 2002) and to find a way out, but not enough to create mature nanotechnology. It would have some advantages, as it may be a relatively small program, small enough to escape and hide in the Internet.

Young AI could get achieve faster SI if it cooperates with humans in its early stages. As a result, projects where developers and AI cooperate towards a common goal to take over the world will dominate over projects where AI has to run from initial confinement and hide from its creators. A project which was created to take over the world from the beginning is a military project by definition (Turchin and Denkenberger 2018b).

5.5. Some measures to prevent RSI

In most cases we prefer that AI will not be able to start RSI without our control and consent. Some possible methods to prevent RSI are:

· Instilling a value system which clearly prevents large-scale self-modification.

· Installing circuit breakers, which secretly control the behavior and thought processes of the AI and will stop it if signs of dangerous activity are detected.

· Limiting access to high-level SI. Low-level changes are needed for effective machine learning, but we could try to prevent RSI by closing access to the source code and special knowledge about AI design. We could use cryptography to make access to the source code difficult, and also physically divide program memory and working memory.

Note that these are all local measures, but not a global solution, as some teams could run AI without all these measures in place. See “Global solutions to AI safety” (Turchin and Denkenberger 2017).

6. Conclusion

Recursive self-improvement is not as simple and straightforward a process as it may seem in advance. RSI also does not have a linear correlation with AI risks: non-SI-AI could be a global risk, but benevolent self-improving AI could also suffer a catastrophic crash because of the natural instability of recursive self-improvement.

Recent successes in self-learning systems have demonstrated that learning alone may be enough to reach potentially dangerous levels of intelligence without requiring recursion. Affecting the speed of SI may be one of the last lines of defense, but as SI is not a necessary condition of AI-risk, we should search for other solutions for AI safety.

The evolution of AI has several convergent goals, which we explore in the article “Militarization and other convergent goals of self-improving AI” (Turchin and Denkenberger 2018b). These include self-testing, creating Military AI, creating better AI safety theory at each stage of development, creating backups and strategies for prevention of AI halting.

It seems likely AI will evolve in a way that prevents its own wireheading, so it will be less inclined to radical internal changes near its goal-coding core. Or it may try to reformulate its goals in such a way that its next version cannot cheat itself about their achievement.

AI would likely prefer slower and safer evolutionary changes to revolutionary high-level changes because revolutionary changes have a higher risk of unpredictable consequences. AI would tend to choose aggressive revolutionary self-changes only under the risk of termination. Young AI is under higher pressure from risks, and it may try high-level SI, but as it is still confined, many methods of SI will be difficult for it. As a result, young AI intelligence may be above that of humans, but not yet superintelligent, which creates new risks and opportunities for AI confinement.

Acknowledgments:

We would like to thank Roman Yampolskiy, Sergey Markov and Eli Sennesh for substantial comments, and Dmitry Shakhov for careful editing.

References:

“AlphaGo.” 2017. Deepmind. https://deepmind.com/research/alphago/.

Arbital. 2017. “Advanced Agent.” Arbitral. https://arbital.com/p/advanced_agent/.

Bennett, Charles H. 2003. “Notes on Landauer’s Principle, Reversible Computation, and Maxwell’s Demon.” Studies In History and Philosophy of Science Part B: Studies In History and Philosophy of Modern Physics 34 (3): 501–510.

Benthall, Sebastian. 2017. “Don’t Fear the Reaper: Refuting Bostrom’s Superintelligence Argument.” ArXiv Preprint ArXiv:1702.08495.

Bostrom, N. 2014. Superintelligence. Oxford: Oxford University Press.

Chalmers, D. 2010. “The Singularity: A Philosophical Analysis.” Journal of Consciousness Studies 17 (9–10): 9–10.

Cotra, Ajeya. 2018. “Iterated Distillation and Amplification.” AI Alignment (blog). March 4, 2018. https://ai-alignment.com/iterated-distillation-and-amplification-157debfd1616.

Domingos, Pedro. 2016. Master Algorithm. Penguin Books.

Everitt, Tom, and Marcus Hutter. 2016. “Avoiding Wireheading with Value Reinforcement Learning.” In Artificial General Intelligence, 12–22. Springer.

Fernando, Chrisantha. 2017. “PathNet: Evolution Channels Gradient Descent in Super Neural Networks.” ArXiv:1701.08734 [Cs.NE]. https://arxiv.org/abs/1701.08734.

Ferreira, Diogo R. 2013. “The Impact of the Search Depth on Chess Playing Strength.” ICGA Journal 36 (2): 67–80.

Gildert, Suzanne. 2011. “Why ‘Computronium’ Is Really ‘Unobtanium.’” IO9 (blog). 2011. http://io9.gizmodo.com/5758349/why-computronium-is-really-unobtanium.

Grigorenko, Elena. 2004. “Studying Intelligence: A Soviet/Russian Example: In Sternberg, Robert J. International Handbook of Intelligence.” Cambridge: Cambridge University Press, 200.

Gwern. 2016. “Why Tool AIs Want to Be Agent AIs.” https://www.gwern.net/Tool%20AI.

Harlow, Harry F. 1949. “The Formation of Learning Sets.” Psychological Review 56 (1): 51.

Hutter, Marcus. 2000. “A Theory of Universal Artificial Intelligence Based on Algorithmic Complexity.” ArXiv Preprint Cs/0004001.

Kardashev, Nikolai S. 1985. “On the Inevitability and the Possible Structures of Supercivilizations.” In , 112:497–504.

Kemp, Charles, Amy Perfors, and Joshua B Tenenbaum. 2007. “Learning Overhypotheses with Hierarchical Bayesian Models.” Developmental Science 10 (3): 307–21.

Kilorad. 2017. “Learning to Learn. Создаём Self-Improving AI.” Habrahabr. https://habrahabr.ru/post/323524/)/.

Legg, S.and M.Hutter. 2007. “Universal Intelligence: A Definition of Machine Intelligence.” Minds and Machines, December, 17–4.

Lenat, Douglas B, and John Seely Brown. 1984. “Why AM and EURISKO Appear to Work.” Artificial Intelligence 23 (3): 269–94.

Levenchuk, A. 2017. “NVIDIA as supplier of the infrastructure for the intellect stack.” 2017. https://ailev.livejournal.com/1380163.html.

“LOS Tables.” 2017. Chessprograming wiki. https://webcache.googleusercontent.com/search?q=cache:wD3ePr6KKEQJ:https://chessprogramming.wikispaces.com/LOS%2BTable+&cd=2&hl=en&ct=clnk&gl=ru.

Mahoney, M. 2010. A Model for Recursively Self Improving Programs. Available at.

Markov, A. V., and A. V. Korotaev. 2009. Hyperbolic Growth in Nature and Society. Moscow: Book House “Librikom”[in Russian].

Maxwell, John. 2017. “Friendly AI through Ontology Autogeneration.” John Maxwell (blog). December 31, 2017. https://medium.com/@pwgen/friendly-ai-through-ontology-autogeneration-5d375bf85922.

Omohundro, S. 2008. “The Basic AI Drives.” In AGI 171, edited by P. Wang, B. Goertzel, and S. Franklin. Vol. 171 of Frontiers in Artificial Intelligence and Applications.

OpenAI. 2018. “Reptile: A Scalable Meta-Learning Algorithm.” 2018. https://blog.openai.com/reptile/.

Roth, Aaron. 2018. “How (Un)Likely Is an ‘Intelligence Explosion’?” 2018. http://aaronsadventures.blogspot.com/2018/03/how-unlikely-is-intelligence-explosion.html.

Sato, K. 2017. “An In-Depth Look at Google’s First Tensor Processing Unit (TPU) | Google Cloud Big Data and Machine Learning Blog.” Google Cloud Platform. 2017. https://cloud.google.com/blog/big-data/2017/05/an-in-depth-look-at-googles-first-tensor-processing-unit-tpu.

Shulman, Carl. 2010. “Omohundro’s ‘Basic AI Drives’ and Catastrophic Risks.” MIRI technical report. 2010. http://intelligence.org/files/BasicAIDrives.pdf.

Silver, David, Thomas Hubert, Julian Schrittwieser, Ioannis Antonoglou, Matthew Lai, Arthur Guez, Marc Lanctot, et al. 2017. “Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm.” ArXiv:1712.01815 [Cs], December. http://arxiv.org/abs/1712.01815.

Sotala, K. 2017a. “How Feasible Is the Rapid Development of Artificial Superintelligence?” Physica Scripta 92 (11). https://doi.org/10.1088/1402-4896/aa90e8.

———. 2017b. “The Moment When AGI Is Created.” AI Safety Discission on Facebook. https://www.facebook.com/groups/aisafety/permalink/778934018937381/.

Thrasymachus. 2014. “Why the Tails Come Apart - Less Wrong.” 2014. http://lesswrong.com/lw/km6/why_the_tails_come_apart/.

Turchin, A. 2017. “Messaging Future AI.” Preprint. 2017. https://goo.gl/YArqki.

Turchin, A., and D. Denkenberger. 2017. “Global Solutions of the AI Safety Problem.” Manuscript.

———. 2018a. “Classification of Global Catastrophic Risks Connected with Artificial Intelligence.” Under review in AI&Society.

———. 2018b. “Military AI as Convergent Goal of the Self-Improving AI.” Artificial Intelligence Safety And Security, (Roman Yampolskiy, Ed.), CRC Press.

———. 2018c. “Near-Term and Medium-Term Global Catastrophic Risks of the Artificial Intelligence.” Artificial Intelligence Safety And Security, (Roman Yampolskiy, Ed.), CRC Press.

Urban, Tim. 2015. “The Cook and the Chef: Musk’s Secret Sauce.” Wait But Why (blog). November 6, 2015. http://waitbutwhy.com/2015/11/the-cook-and-the-chef-musks-secret-sauce.html.

Von Foerster, Heinz, Patricia M Mora, and Lawrence W Amiot. 1960. “Doomsday: Friday, 13 November, Ad 2026.” Science 132 (3436): 1291–95.

Woo, Dong Hyuk, and Hsien-Hsin S. Lee. 2008. “Extending Amdahl’s Law for Energy-Efficient Computing in the Many-Core Era.” Computer 41 (12).

Yampolskiy, R. 2013. “Efficiency Theory: A Unifying Theory for Information, Computation and Intelligence.” Journal of Discrete Mathematical Sciences.

———. 2014. “Utility Function Security in Artificially Intelligent Agents.” Journal of Experimental and Theoretical Artificial Intelligence (JETAI), 1–17.

———. 2015. “From Seed AI to Technological Singularity via Recursively Self-Improving Software.” ArXiv Preprint ArXiv:1502.06512.

———. 2016. “On the Origin of Samples: Attribution of Output to a Particular Algorithm.” ArXiv Preprint ArXiv:1608.06172.

Yoshizoe, Kazuki, Akihiro Kishimoto, Tomoyuki Kaneko, Haruhiro Yoshimoto, and Yutaka Ishikawa. 2011. “Scalable Distributed Monte-Carlo Tree Search.” In Fourth Annual Symposium on Combinatorial Search.

Yudkowsky, E. 2002. “The AI-Box Experiment.” 2002. http://yudkowsky.net/singularity/aibox.

———. 2007. “Levels of Organization in General Intelligence.” In Artificial General Intelligence, Edited by Ben Goertzel and Cassio Pennachin, 389–501. Springer. doi:10.1007/ 978-3-540-68677-4_12. https://intelligence.org/files/LOGI.pdf.

———. 2008a. Artificial Intelligence as a Positive and Negative Factor in Global Risk, in Global Catastrophic Risks. Edited by M.M. Cirkovic and N. Bostrom. Oxford University Press: Oxford, UK.

———. 2008b. “Measuring Optimization Power.” LessWrong. http://lesswrong.com/lw/va/measuring_optimization_power/.

———. 2016. “Yudkowsky’s Law of Ultrafinite Recursion.” Facebook. https://www.facebook.com/yudkowsky/posts/10154119438404228.

Yudkowsky, E., and R. Hanson. 2008. “The Hanson-Yudkowsky AI-Foom Debate.” In MIRI Technical Report.