I don't think the evidence provided substantiates the conclusions in this post. Overall it looks like you've demonstrated this:
- They didn't commit obvious fraud (last digit test)
- If you remove all 14 of their control variables, this removes much of their statistical power, so the results are only marginally significant (p = 0.026981 overall, compare p < 0.01 in many independent categories in the original)
- If you remove all 14 of their control variables AND change from Poisson to negative binomial, the results are no longer significant. (However, if you include the control variables and use negative binomial the results are still significant: Web Table 12 in appendix)
Furthermore you only examine all cause mortality, whereas the study examines deaths from specific diseases. Your replication will be less powered because even in non-high-income countries most people die from things like heart disease and stroke, reducing your power to detect even large changes in malaria or HIV deaths caused by USAID. Removing all 14 controls will kill your statistical power further, because the presence of things like "adequate sanitation" and "health expenditure" will definitely affect the mortality rate.
Finally, in your conclusion, it makes no sense to say "some of the choices they make to strengthen the result end up being counterproductive"--this is weak evidence against p-hacking that to my mind cancels the weak evidence you found for p-hacking! This is super unvirtuous, don't just assume they were p-hacking and say your belief is confirmed when you found some weak evidence for and some weak evidence against.
Off the top of my head, here are the results I'd want to see from someone skeptical of this study, in increasing order of effort. I agree these would be much easier if they shared their full data.
- Think about whether the causal story makes sense (is variance in USAID funding exogenous and random-ish?)
- Add year-based fixed effects
- Some kind of exploratory analysis to decide whether the negative binomial model is appropriate. I have never fit a negative binomial model but here's what o3 suggests
- Use a Poisson model with robust standard errors
- Multiverse analysis where you pick 20 plausible control variables, control for 10 of them, and see how many are significant
Now some comments in no particular order:
First thanks for including the equations, it makes the post a lot easier to understand.
when the world’s foremost medical journal publishes work indicating that a policy’s results will be comparable in death count to history’s engineered mass-starvations by year’s end, I’m going to be skeptical.
I'm as skeptical of this as any other study, but we should beware the absurdity heuristic and instead think about the actual claimed mechanism. There are LOTS more people in LMICs in the world today than in 1932 Ukraine and we know that millions die from preventable diseases per year; we also know that one of the main goals of USAID is to reduce deaths from preventable diseases, and that spending enough resources on preventable diseases can basically eliminate them.
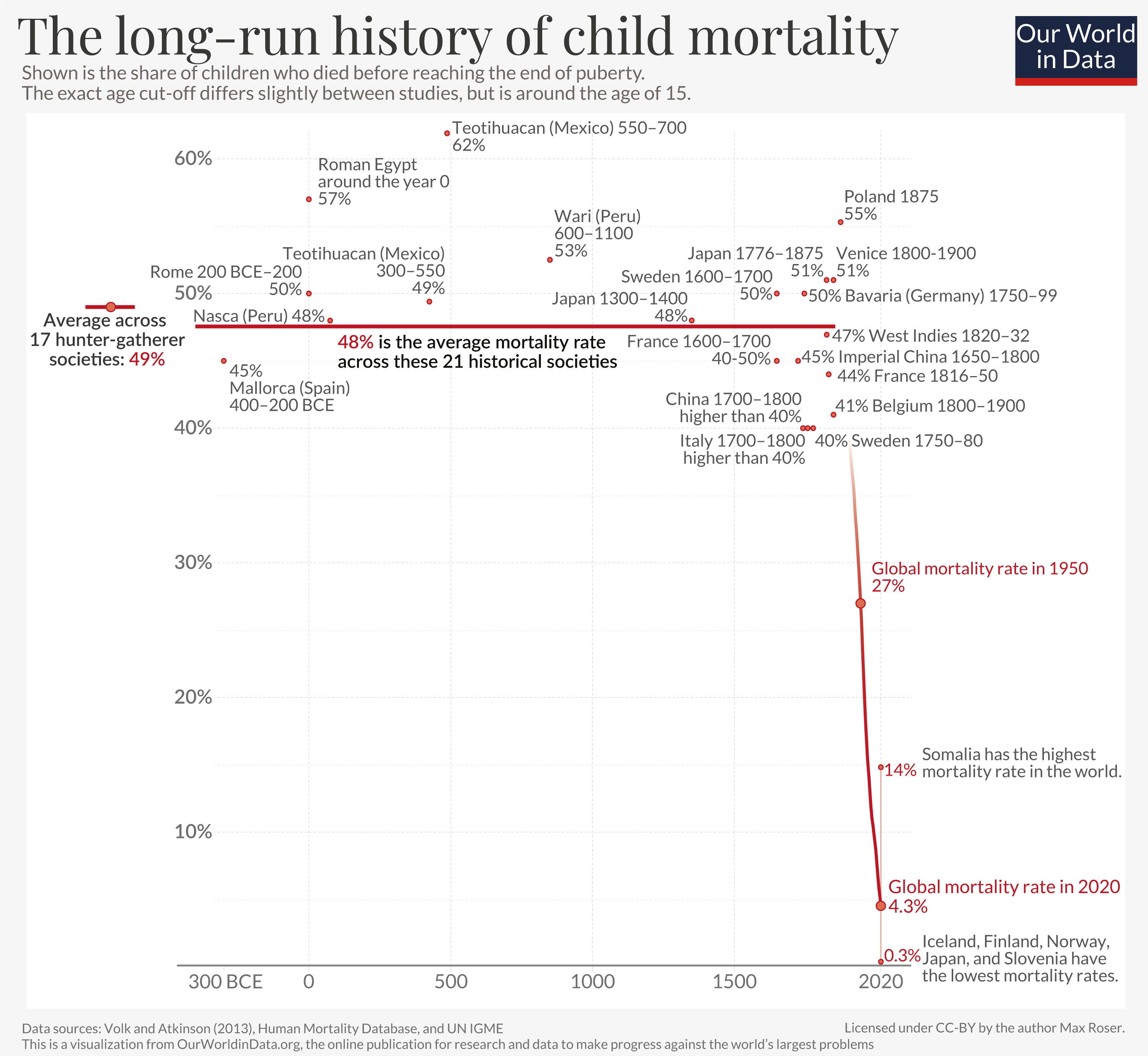
I’m going to be triply skeptical when similar Monte Carlo modeling has led to inflated and incorrect death count prognostications in the past.
There are at least two reasons I don't think these cases are similar.
- The link you shared is about inherently harder modeling than this Lancet study. Ferguson's model models the exponential spread of transmissible diseases, which inherently has orders of magnitude wide confidence intervals in the final number of deaths, especially for median vs worst case scenarios. The only thing these studies share is they're using the extremely common technique of Monte Carlo modeling, and they're about disease.
- The prediction that 500k people would die without a lockdown in the UK, and 2M in the US, isn't too far off, given that even with partial lockdowns + vaccination 232k died in the UK and 1.19M in the US, plus there was limited information at the time
It’s way too much work for me to go find and recreate all of the 18(!) control variables they use.
They have 14 control variables not 18: 4 time based controls and 10 other controls.
The per year binning also torpedoes their results.
This is interesting, I'd like to see it with the full methodology
It looks a slightly better fit from a BIC perspective. The second quartile drops from significance and the third quartile is barely significant. Overall, this is still a much weaker result than what they report, but the binning itself doesn’t change a lot about the regression.
Note their ** means p < 0.05 and their *** means p < 0.01, which is different from your annotations
The weird thing about this paper is its relation to Regression 1. In my reproduction that doesn’t have a gazillion controls, there is a significant relationship between per capita USAID spend and overall mortality. For whatever reason this wasn’t enough and some of the choices they make to strengthen the result end up being counterproductive. In both the categorical binning issue and the choice to use Poisson, the alternative choices make the results null, which I consider to be fairly strong evidence of p-hacking.
My understanding is that when you replaced their experiment with a simpler, much less powerful experiment, then did a cursory sensitivity analysis, the results were sometimes significant and sometimes not significant. This is totally expected. Also it makes no sense to say "some of the choices they make to strengthen the result end up being counterproductive"--this is weak evidence against p-hacking that to my mind cancels the weak evidence you found for p-hacking! This is super unvirtuous, don't just assume they were p-hacking and say your belief is confirmed when you found some weak evidence for and some weak evidence against.
Also, the results are significant in so many categories that I disagree with p-hacking being likely here. If you aggregated the results in some principled way, you would get some crazy low value like 10^-50, so it can't be a multiple comparisons issue. As for the controls, they seem plausible on priors (I'm not familiar enough to know if they're standard), and seem to improve the predictive power of the model.
Thanks for the thoughtful comment. I'll try to address these remarks in order. You state
Furthermore you only examine all cause mortality, whereas the study examines deaths from specific diseases.
They also use overall mortality (Web Table 10), which is what I was trying to reproduce and screenshotted. The significance figures aren't really different than those for the regressions broken down by mortality cause (Web Table 15), but the rate ratios for the all cause mortality ratios are clearly smaller in the disaggregated regressions because people die from other stuff. I mostly ignored the rate ratio sizes and focused on the significances here, but agree the most powerful effects probably result from the disaggregated regressions.
Removing all 14 controls will kill your statistical power further, because the presence of things like "adequate sanitation" and "health expenditure" will definitely affect the mortality rate. ... they seem plausible on priors (I'm not familiar enough to know if they're standard), and seem to improve the predictive power of the model.
This is a fundamental misunderstanding of how controls work and what they're supposed to do. Just yesterday Cremieux wrote a pretty good piece on this very topic. The authors include these controls with little thought to the underlying causal mechanism. Their only remarks on them at all in the supplemental material are
These controls, combined with country fixed-effects models and other isolation factors, help refine the relationship between USAID per capita and changes in mortality over time.
This isn't necessarily true at all. Consider one of the controls: Health expenditure as a percent of GDP. Is that a confounder, influencing USAID spend levels and mortality rates simultaneously? Is it a collider, caused by increased or decreased USAID spend and mortality changes? In the former case, yes, go ahead and control for it, but if it's the latter, it screws up the analysis. Both are plausible. The authors consider neither.
I did apparently miscount the controls. It's unclear why their own spec on page 13 miscounts them as well.
You mention the Monte Carlo simulations aren't comparable. This is a fair, and I really like the explanation. I didn't really touch on that aspect of this analysis in the post, but you've persuaded me I'm making a cheap point.
"Also it makes no sense to say "some of the choices they make to strengthen the result end up being counterproductive".
This was unclear, and I regret it. I meant counterproductive in the sense of complicating the analysis. I'm still not clear how they got such strong, consistent results. My suspicions is careful control selection as alluded to above.
“There was an old bastard named Lenin
Who did two or three million men in.
That’s a lot to have done in
But where he did one in
That old bastard Stalin did ten in.”
—Robert Conquest
The current administration’s rollup of USAID has caused an amount of outrage that surprised me, and inspired anger even in thoughtful people known for their equanimity. There have been death counters. There have been congressional recriminations. At the end of last month, the Lancet published Cavalcanti et al. which was entitled Evaluating the impact of two decades of USAID interventions and projecting the effects of defunding on mortality up to 2030: a retrospective impact evaluation and forecasting analysis.
This paper uses some regressions and modeling to predict, among other things, that almost 1.8M people are expected to die in 2025 alone from the USAID-related cuts.
I have no love for the administration or many of its actions, but when the world’s foremost medical journal publishes work indicating that a policy’s results will be comparable in death count to history’s engineered mass-starvations by year’s end, I’m going to be skeptical. I’m going to be doubly skeptical when the same work also indicates this policy’s results will be comparable in death count to Maoist China’s policy results by 2030. I’m going to be triply skeptical when similar Monte Carlo modeling has led to inflated and incorrect death count prognostications in the past. And so on.
The BLUF is that the regressions in this paper are likely p-hacked in a way that probably undermines the conclusions. The rest of this post will be a semi-organized cathexis focused on my skepticism.
Regression analysis
The backbone of this paper is a collection of regression analyses. Each is an effort to see how well USAID spend has been statistically related to different measures of mortality by country and over time. In any given year, such an analysis might be fruitless or underpowered; the idea is to use panel data which captures USAID spend over a collection of years and mortality over the same collection of years. In this case they look at 133 countries over 20 years from 2001 to 2021. To the stats mavens out there, this is a panel based Poisson regression analysis with a variety of controls and country-level fixed effects, like this.
log(μit)=log(popit)+3∑q=0βqUSAIDqit+8∑s=4βsTy+18∑k=9βkXkit+αi+uitThis is a complicated analysis, and a lot of technical choices have to be made in order to do it defensibly. Choices like which countries to include, which years to include, which controls to include, how to repair the control variables with missing data, how to deal with exogenous disaster events, which model specification to use, and on and on. It’s choices all the way down. This fact leaves many degrees of freedom that can affect interpretation of the final results.
In mitigation, the authors publish 50 pages of supplementary material to defend the decisions they’ve made. It’s great. I enjoyed reading most of it. It’s better than what many papers do.
In aggravation, and to my slack-jawed disbelief, there is no link to either the flattened data or the code used to produce the regression analyses or the figures. The team of authors is large and they needed to share code and data and stuff. A code repository almost certainly exists for this project and still it remains hidden. In the following sections where I attempt a partial replication, I had to go get and process the data elements myself, and I kind of resent it.
Rant over. For several USAID targeted causes of death, the authors report a collection of regressions as described above and arrive at their Figure 1.
So each dot is a regression coefficient corresponding to a rate ratio. For example, the first row implies “Low USAID per capita spend is estimated to decrease Tuberculosis mortality by 100 - 86 = 14%, and that result is significant at the p < 0.05 level”. The striking sixth row implies “High USAID per capita spend is estimated to decrease HIV mortality by 100 - 35 = 65%, and that result is significant at the p < 0.01 level”.
I have done regressions like this on real world data for a long time. This isn’t some toy dataset you’d use in a college problem set; it’s created from diverse and disparate data sources. I don’t know how else to say this, but practitioners who work on such data know that nothing works as cleanly as this the first time you do it, and probably not even when you refine the technical choices iteratively. The results are always noisier and less significant than you’d prefer.
Everything in this alarming figure is significant except for the sanity test regression they use at the bottom. Each of the eight regressions has the perfect, expected ordering between high, medium, and low levels of spend!
Remember, they’re using mortality data that specifically and intentionally comes from the poorer countries where USAID had a large footprint. The Bird recently wrote a great piece about how such countries lack the capacity to collect data effectively and it’s a huge problem in the developing world. The WHO even has a specific webpage about data quality and a tool allowing you to see how bad some of the data quality is in poor countries.
In the FAQ they allege this explicitly.
Look, suppose none of this is true. Suppose the WHO is wrong and the GBD mortality data quality in these regressions is fine, and further suppose that the USAID spend really was very effective at mortality reduction in the ways the regressions above work. Suppose that in each regression there was an 80% chance of the high > medium > low pattern holding in mortality reduction. Assuming some kind of independence of the disease mortality and individual regression analyses, you’re still only going to see this pattern .8 ^ 8 = 16.7% of the time.
What’s going on here?
I was sufficiently suspicious of this that I actually did a last digit uniformity test on some of the rate ratio statistics. `web15Values` are from Web Figure 15 in the supplemental material, which are the same ones reported in Figure 1.
So this test was fine, and probably excludes the possibility that people are literally just making up numbers.
A partial reproduction
I did attempt a partial reproduction of the results in this paper. The supplementary material contains a lot of discussion around robustness of the results to changes in the modeling decisions. Unfortunately, with no code or flattened data, there’s no way of actually testing this directly and you have to start from scratch. This section will be devoted to a significantly simpler model specification than what the authors used. The goal here is not a faithful reproduction. It’s way too much work for me to go find and recreate all of the 18(!) control variables they use.
Instead the idea to determine the sensitivity of the analysis of some of the modeling decisions. To keep this simple, for the rest of this section we’ll be regressing all-cause mortality on the USAID per capita spend variables, as done in Web Table 7, pages 17 and 18 in the supplementary material. There will be no controls or dummy variables, and the spec will be thereby simplified as
log(μit)=log(popit)+3∑q=0βqUSAIDqit+αi+uitThe code and data I used in the rest of this analysis is checked in here.
Choice to use categorical spend exposures
In the paper’s regressions, you’ll notice that a variable like `per_capita_spend` does not appear. There are only a collection of variables like high, medium and low USAID spend. This is because the authors chose to bucket the per capita spend statistics into quartile buckets. On this subject they state
I don’t really agree with any of this. I get they’re writing for an epidemiological, policy-based audience, but that audience agrees with them the USAID cuts are terrible regardless of the model spec. They’re also writing to suggest the USAID cuts amount to 7-figure mass murder, so you don’t take shortcuts when doing the statistics just because it’s easier to understand. There are better ways to deal with outliers and overdispersion than crude feature binning that can introduce arbitrary threshold effects.
As for the “causal interpretation”, a dose-response curve only sort of bolsters the case for the More USAID spend → Less Death model of causation. It’s also consistent with a More Death → More USAID Spend model of causation where spend is increased to deal with serious mortality crises.
This is a difference of opinion though; what does their choice to bin the variables this way actually do?
I ran this with a continuous exposure variable (no binning) and obtained Regression 1
Ok, so maybe there is some there there. What does it look like with the quartile binning?
It looks a slightly better fit from a BIC perspective. The second quartile drops from significance and the third quartile is barely significant. Overall, this is still a much weaker result than what they report, but the binning itself doesn’t change a lot about the regression.
I actually had trouble getting this far. When I did the binning initially, my quartiles kept coming out much different than what the authors had calculated. I finally realized that they must have binned them not per year but across the entire data. Regarding how this quartile binning was done, the authors state in the supplemental material that
I took this to mean per year binning, but it’s not. They must have done it over the entire dataset because this is what happens when you do the per year binning.
Suddenly, the results become confused and unpublishable with this spec.
I’d pretty sure the choice to do per year binning is correct. They explicitly chose not to include year-based fixed effects so any trends in funding levels are not correctly handled if you do it over the entire dataset. The per year binning also torpedoes their results.
Choice to use Poisson
Throughout this paper, the authors use Poisson regression to model the country level mortality. In lay terms, this sort of assumes deaths happen independently of each other and at a predictable rate. Obviously, USAID intentionally operates in parts of the world where Death might be omnipresent, joined by his three companion horsemen Conquest, Famine, and War who don’t necessarily respect statistical independence.
But ignoring this notion, Poisson is standard for something like this, and I don’t blame the authors for defaulting to this spec. However, given the noise in this mortality data I wondered whether it would be better to use a negative binomial regression, and the authors wondered the same thing.
In a bizarre technical twist, the BICs for negative binomial and Poisson models as implemented in R are incomparable. The authors worked in stata and I’m sure as shit not paying for that to do a replication. I can’t easily confirm that the Poisson BIC was better than the negative binomial BIC, but a few things about this are noteworthy. The Poisson regression summary I did is Regression 2 above. Compare this to the corresponding negative binomial regression
There are a few salient things to note about this comparison between Regression 2 and Regression 4.
First, the NB regression theta indicates mild to moderate overdispersion, so all other things equal, NB is probably going to be better. But unfortunately for the authors, look at the p-values! Such a regression would completely blow up their results. Nothing is significant at all.
Second, the rate ratios in the NB regression are much smaller than the authors report in Web Table 7 and in the Poisson regression.
Third, you do see the expected ordering of the spend quartile variables in the Poisson regression so maybe there is some there there, but it’s messier in the NB regression.
Fourth, from a personal perspective, the piece of crap NB model is much more like what I’d expect to see on messy real world data like this.
In this circumstance, both choices are probably defensible with NB probably being marginally better, but naturally they went with the methodology making the results impressive. Make of that what you will.
Choice of countries
The authors chose to exclude high income countries from the regression. I concur, and that’s what I did in the above sections. However, I did want to see how sensitive the result in Regression 1 was to changes in the country composition among the countries I used.
I ran a quick 1000 model simulation randomly dropping 10% of the low income countries from the dataset and tracking what the p-values and spend coefficients looked like.
The red lines are the coefficient and p-value from Regression 1. I couldn’t check the exact 133 countries the author’s used (I only ended up with 129, which was probably because we bucketed the income levels slightly differently) but there’s nothing egregious here. It is interesting that when you drop the correct set of countries in these regressions, the spend effects basically go to zero, but this doesn’t happen very often.
This indicates quite a bit of robustness to different country selection, so no complaints there.
Coda
The weird thing about this paper is its relation to Regression 1. In my reproduction that doesn’t have a gazillion controls, there is a significant relationship between per capita USAID spend and overall mortality. For whatever reason this wasn’t enough and some of the choices they make to strengthen the result end up being counterproductive. In both the categorical binning issue and the choice to use Poisson, the alternative choices make the results null, which I consider to be fairly strong evidence of p-hacking.
Even so, without the controls, I could not make a result nearly as strong as what’s reported. It is possible that the controls they use make all of the exposure variables much more significant, but that’s not been the case in my experience. If you need to use a ton of controls to get there, the underlying relationship probably isn’t strong as you believe.
A weak result isn’t actually that controversial. Other modern studies using similar methods have come to that conclusion.
On a non-statistical note, maybe I lack imagination, but it simply isn’t believable that millions of people are going to die because of USAID’s demise. Even though it’s published in the Lancet, please reserve judgement.