A more important difference - and a more genuine criticism of this analogy - is that mathematical physics is of course applied to the real, natural world. And perhaps there really is something about nature that makes it fundamentally amenable to mathematical description in a way that just won't apply to a large neural network trained by some sort of gradient descent? Indeed one does have the feeling that the endeavour we are focussing on would have to be underpinned by a hope that there is something sufficiently 'natural' about deep learning systems that will ultimately make at least some higher-level aspects of them amenable to mathematical analysis. Right now I cannot say how big of a problem this is.
There is no difference between natural phenomena and DNNs (LLMs, whatever). DNNs are 100% natural, don't you seriously believe there is something supernatural in their working? Hence, the criticism is invalid and the problem is non-existent.
See "AI as physical systems" for more on this. And in the same vein: "DNNs, GPUs, and their technoevolutionary lineages are agents".
I think that a lot of AI safety and AGI capability researchers are confused about this. They see information and computing as mathematical rather than physical. The physicalism of information and computation is a very important ontological commitment one has to make to deconfuse oneself about AI safety. If you wish to "take this pill", see Fields et al. (2022a), section 2.
I think the above confusion of the study of AI as mathematics (rather than physics and cognitive science -- natural sciences) leads you and some other people that new mathematics has to be developed to understand AI (I may misinterpret you, but it definitely seems from the post that you think this is true, e. g. from your example of algebraic topology). It might be that we will need new mathematics, but it's far from certain. As an example, take "A mathematical framework for transformer circuits": it doesn't develop new mathematics. It just uses existing mathematics: tensor algebra.
I think the research agenda of "weaving together theories of cognition and cognitive development, ML, deep learning, and interpretability through the abstraction-grounding stack" could plausibly lead to the sufficiently robust and versatile understanding of DNNs that we want[1], without the need to develop much or any new mathematics along the way.
Here's what the "abstraction-grounding stack" looks like:
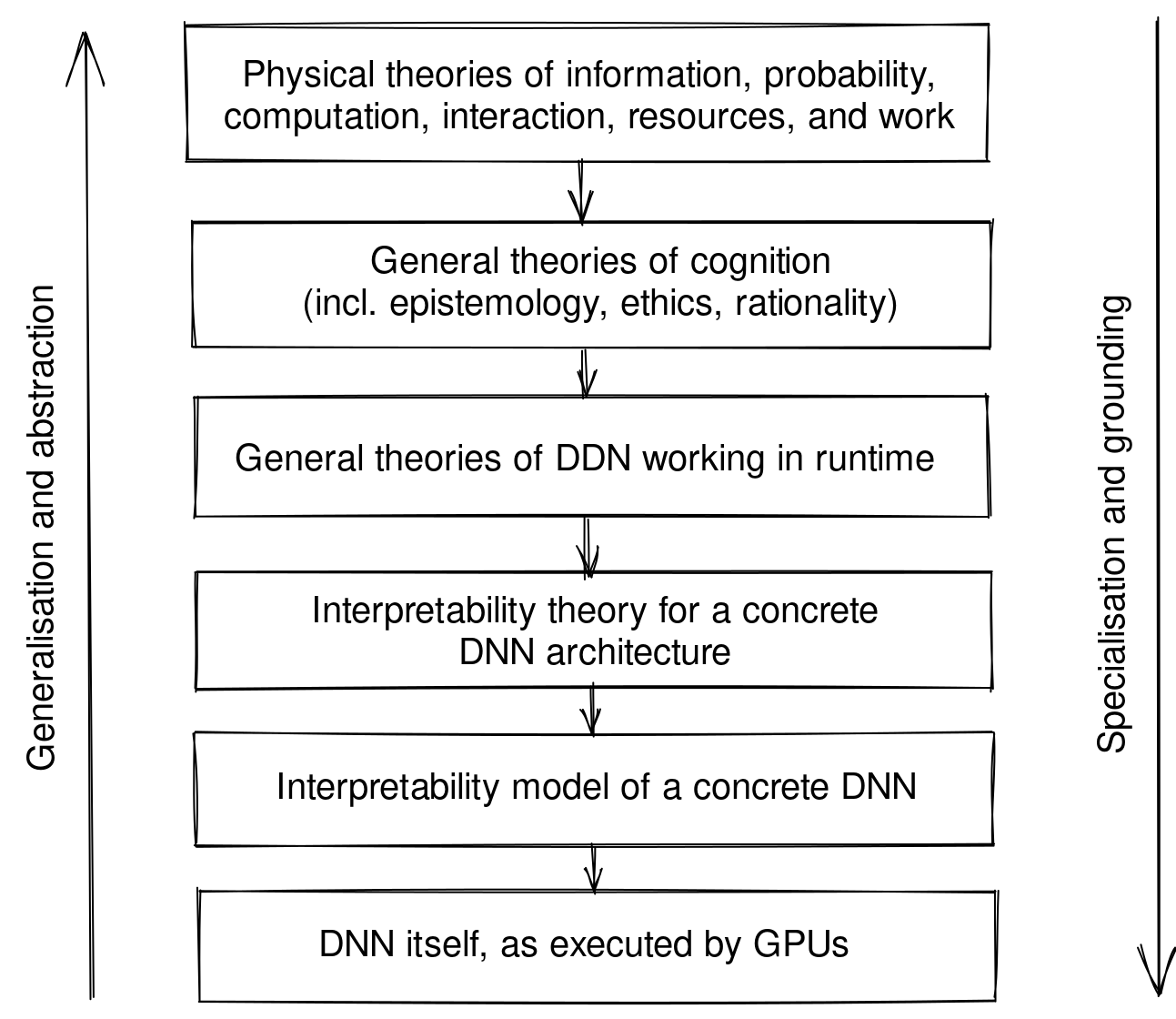
Many of the connections between theories of cognition and cognitive development at different levels of specificity are not established yet, and therefore present a lot of opportunities to verify the specific mechanistic interpretability theories:
- I haven’t heard of any research attempting to connect FEP/Active Inference (Fields et al. 2022a; Friston et al. 2022) with many theories of DNNs and deep learning, such as Balestriero (2018), Balestriero et al. (2019), or Roberts, Yaida & Hanin (2021). Note that Marciano et al. (2022) make such a connection between their own theory of DNNs and Active Inference. Apart from Active Inference, some other theories of intelligence and cognition (Boyd et al. 2022; Ma et al. 2022) are “ML-first” and thus cover both “general cognition” and “ML” levels of description at once.
- On the next level, interpretability theories (at least those authored by Anthropic) are not yet connected to any general theories of cognition, ML, DNNs, or deep learning. In particular, I think it would be very interesting to connect theories of polysemanticity (Elhage et al. 2022; Scherlis et al. 2022) with general theories of contextual/quantum cognition (see Basieva et al. (2021), Pothos & Busemeyer (2022), and Fields & Glazebrook (2022) for some recent reviews, and Fields et al. (2022a) and Tanaka et al. (2022) for examples of recent work).
- I make a hypothesis about a “skip-level” connection between quantum FEP (Fields et al. 2022a) and the circuits theory (Olah et al. 2020), identifying quantum reference frames with features in DNNs. This connection should be checked and compared with Marciano et al. (2022).
- All the theories of polysemanticity (Elhage et al. 2022; Scherlis et al. 2022) and grokking (Liu et al. 2022; Nanda et al. 2023) make associative connections to phase transitions in physics, but, as far as I can tell, none of these theories has yet been connected with physical theories of dynamical systems, criticality, and emergence more rigorously and attempted to propose some falsifiable predictions about the behaviour of NNs that would follow from the physical theories.
- Fields et al. (2022b) propose topological quantum neural networks (TQNNs) as a general framework of neuromorphic computation, and some theory of their development. Marciano et al. (2022) establish that DNNs are a semi-classical limit of TQNNs. To close the “developmental” arc, we should identify how the general theories of neuromorphic development, evolution, and selection map on the theories of feature and circuit development, evolution, and selection inside DNNs or, specifically, transformers.
- I don’t yet understand, how, but perhaps the connections between ML, fractional dynamics, and renormalisation group, identified by Niu et al. (2021), could help to better understand, verify, and contextualise some mechanistic interpretability theories as well.
- ^
I'd restrain from saying "general theory" because general theories of DNNs already exist, and in large numbers. I'm not sure these theories are insufficient for our purposes and new general theories should be developed. However, what indeed is definitely lacking are the connections between the theories throughout the "abstraction-grounding stack". This is explained in more detail in the description of the agenda. See also the quote from here: "We (general intelligences) use science (or, generally speaking, construct any models of any phenomena) for the pragmatic purpose of being able to understand, predict and control it. Thus, none of the disciplinary perspectives on any phenomena should be regarded as the “primary” or “most correct” one for some metaphysical or ontological reasons. Also, this implies that if we can reach a sufficient level of understanding of some phenomenon (such as AGI) by opportunistically applying several existing theories then we don’t need to devise a new theory dedicated to this phenomenon specifically: we already solved our task without doing this step."
>There is no difference between natural phenomena and DNNs (LLMs, whatever). DNNs are 100% natural
I mean "natural" as opposed to "man made". i.e. something like "occurs in nature without being built by something or someone else". So in that sense, DNNs are obviously not natural in the way that the laws of physics are.
I don't see information and computation as only mathematical; in fact in my analogies I write that the mathematical abstractions we build as being separate from the things that one wants to describe or make predictions about. And this applies to the computations in NNs too.
I don't want to study AI as mathematics or believe that AI is mathematics. I write that the practice of doing mathematics will only seek out the parts of the problem that are actually amenable to it; and my focus is on interpretability and not other places in AI that one might use mathematics (like, say, decision theory).
You write "As an example, take "A mathematical framework for transformer circuits": it doesn't develop new mathematics. It just uses existing mathematics: tensor algebra.:" I don't think we are using 'new mathematics' in the same way and I don't think the way you are using it commonplace. Yes I am discussing the prospect of developing new mathematics, but this doesn't only mean something like 'making new definitions' or 'coming up with new objects that haven't been studied before'. If I write a proof of a theorem that "just" uses "existing" mathematical objects, say like...matrices, or finite sets, then that seems to have little bearing on how 'new' the mathematics is. It may well be a new proof, of a new theorem, containing new ideas etc. etc. And it may well need to have been developed carefully over a long period of time.
I feel that you are redefining terms. Writing down mathematical equations (or defining other mathematical structures that are not equations, e.g., automata), describing natural phenomena, and proving some properties of these, i.e., deriving some mathematical conjectures/theorems, -- that's exactly what physicists do, and they call it "doing physics" or "doing science" rather than "doing mathematics".
I mean "natural" as opposed to "man made". i.e. something like "occurs in nature without being built by something or someone else". So in that sense, DNNs are obviously not natural in the way that the laws of physics are.
I wonder how would you draw the boundary between "man-made" and "non-man-made", the boundary that would have a bearing on such a fundamental qualitative distinction of phenomena as the amenability to mathematical description.
According to Fields et al.'s theory of semantics and observation ("quantum theory […] is increasingly viewed as a theory of the process of observation itself"), which is also consistent with predictive processing and Seth's controlled hallucination theory which is a descendant of predictive processing, any observer's phenomenology is what makes mathematical sense by construction. Also, here Wolfram calls approximately the same thing "coherence".
Of course, there are infinite phenomena both in "nature" and "among man-made things" the mathematical description of which would not fit our brains yet, but this also means that we cannot spot these phenomena. We can extend the capacity of our brains (e.g., through cyborgisation, or mind upload), as well as equip ourselves with more powerful theories that allow us to compress reality more efficiently and thus spot patterns that were not spottable before, but this automatically means that these patterns become mathematically describable.
This, of course, implies that we ought to make our minds stronger (through technical means or developing science) precisely to timely spot the phenomena that are about to "catch us". This is the central point of Deutsch's "The Beginning of Infinity".
Anyway, there is no point in arguing this point fiercely because I'm kind of on "your side" here, arguing that your worry that developing theories of DL might be doomed is unjustified. I'd just call these theories scientific rather than mathematical :)
I'm skeptical, but I'd love to be convinced. I'm not sure that it's necessary to make interpretability scale, but it definitely strikes me as a potential trump card that would allow interpretability research to keep pace with capabilities research.
Here are a couple relatively unsorted thoughts (Keep in mind that I'm not a mathematician!):
- Deep learning as a field isn't exactly known for its rigor. I don't know of any rigorous theory that isn't as you say purely 'reactive', with none of it leading to any significant 'real world' results. As far as I can tell this isn't for a lack of trying either. This has made me doubt its mathematical tractability, whether it's because our current mathematical understanding is lacking or something else (DL not being as 'reductionist' as other fields?). How do you lean in this regard? You mentioned that you're not sure when it comes to how amenable interpretability itself is, but would you guess that it's more or less amenable than deep learning as a whole?
- How would success of this relate to capabilities research? It's a general criticism of interpretability research that it also leads to heightened capabilities, would this fare better/worse in that regard? I would have assumed that a developed rigorous theory of interpretability would probably also entail significant development of a rigorous theory of deep learning.
- How likely is it that the direction one may proceed in would be correct? You mention an example in mathematical physics, but note that it's perhaps relatively unimportant that this work was done for 'pure' reasons. This is surprising to me, as I thought that a major motivation for pure math research, like other blue sky research, is that it's often not apparent whether something will be useful until it's well developed. I think this is the similar to you mentioning that the small scale problems will not like the larger problem. You mention that this involves following one's nose mathematically, do you think this is possible in general or only for this case? If it's the latter, why do you think interpretability is specifically amenable to it?
Thanks very much for the comments I think you've asked a bunch of very good questions. I'll try to give some thoughts:
Deep learning as a field isn't exactly known for its rigor. I don't know of any rigorous theory that isn't as you say purely 'reactive', with none of it leading to any significant 'real world' results. As far as I can tell this isn't for a lack of trying either. This has made me doubt its mathematical tractability, whether it's because our current mathematical understanding is lacking or something else (DL not being as 'reductionist' as other fields?). How do you lean in this regard? You mentioned that you're not sure when it comes to how amenable interpretability itself is, but would you guess that it's more or less amenable than deep learning as a whole?
I think I kind of share your general concern here and I’m uncertain about it. I kind of agree that it seems like people had been trying for a while to figure out the right way to think about deep learning mathematically and that for a while it seemed like there wasn’t much progress. But I mean it when I say these things can be slow. And I think that the situation is developing and has changed - perhaps significantly - in the last ~5 years or so, with things like the neural tangent kernel, the Principles of Deep Learning Theory results and increasingly high-quality work on toy models. (And even when work looks promising, it may still take a while longer for the cycle to complete and for us to get ‘real world’ results back out of these mathematical points of view, but I have more hope than I did a few years ago). My current opinion is that certain aspects of interpretability will be more amenable to mathematics than understanding DNN-based AI as a whole .
How would success of this relate to capabilities research? It's a general criticism of interpretability research that it also leads to heightened capabilities, would this fare better/worse in that regard? I would have assumed that a developed rigorous theory of interpretability would probably also entail significant development of a rigorous theory of deep learning.
I think basically your worries are sound. If what one is doing is something like ‘technical work aimed at understanding how NNs work’ then I don’t see there as being much distinction between capabilities and alignment ; you are really generating insights that can be applied in many ways, some good some bad (and part of my point is you have to be allowed to follow your instincts as a scientist/mathematician in order to find the right questions). But I do think that given how slow and academic the kind of work I’m talking about is, it’s neglected by both a) short timelines-focussed alignment people and b) capabilities people.
How likely is it that the direction one may proceed in would be correct? You mention an example in mathematical physics, but note that it's perhaps relatively unimportant that this work was done for 'pure' reasons. This is surprising to me, as I thought that a major motivation for pure math research, like other blue sky research, is that it's often not apparent whether something will be useful until it's well developed. I think this is the similar to you mentioning that the small scale problems will not like the larger problem. You mention that this involves following one's nose mathematically, do you think this is possible in general or only for this case? If it's the latter, why do you think interpretability is specifically amenable to it?
Hmm, that's interesting. I'm not sure I can say how likely it is one would go in the correct direction. But in my experience the idea that 'possible future applications' is one of the motivations for mathematicians to do 'blue sky' research is basically not quite right. I think the key point is that the things mathematicians end up chasing for 'pure' math/aesthetic reasons seem to be oddly and remarkably relevant when we try to describe natural phenomena (iirc this is basically a key point in Wigner's famous 'Unreasonable Effectiveness' essay.) So I think my answer to your question is that this seems to be something that happens "in general" or at least does happen in various different places across science/applied math
Hey Spencer,
I realize this is a few months late and I'll preface with the caveat that this is a little outside my comfort area. I generally agree with your post and am interested in practical forward steps towards making this happen.
Apologies for how long this comment turned out to be. I'm excited about people working on this and based on my own niche interests have takes on what could be done/interesting in the future with this. I don't think any of this is info hazardy in theory but significant success in this work might be best kept on the down low.
Some questions:
- Why call this a theory of interpretability as opposed to a theory of neural networks? It seems to me that we want a theory of neural networks. To the extent this theory succeeds, we would expect various outcomes like the ability a priori to predict properties or details of neural networks. One such property we would expect, as with physical systems, might be to take measurements of some properties of a system and map them to other properties (such as the ideal gas equation). If you thought it was possible to develop a more specific theory only dealing with something like interpreting interventions in neural networks (eg causal tracing) then this might be better called a theory of interpretability. To the extent Mendel understood much of inheritance prior to us understanding the structure of DNA, there might be insights to be gained without building a theory from the ground up, but my sense is that's the kind of theory you want.
- have you made any progress on this topic or do you know anyone who would describe this explicitly as their research agenda? If so what areas are they working in.
Some points:
- One thing I struggle to understand, and might bet against is that this won't involve studying toy models. To my mind, Neel's grokking work, Toy Models of Superposition, Bhillal's "A Toy Model of Universality: Reverse Engineering How Networks Learn Group Operations" all seems to be contributing towards important factors that no comprehensive theory of Neural Networks could ignore. Specifically, the toy models of superposition work shows concepts like importance, sparsity and correlation of features being critical to representations in neural networks. Neel's progress measures work (and I think at least one other anthropic paper) address memorisation and generalization. Bhillal's work shows composition of features into actual algorithms. I emphasize all of these because even if you thought an eventual comprehensive mathematical theory would use different terminology or reinterpret those studied networks differently, it seems highly likely that it would use many of those ideas and essential that it explain similar phenomena. I think other people have already taughted heavily the successes of these works so I'll stop there and summarize this point as: if I were a mathematician, I'd start with these concepts and build them up to explain more complex systems. I'd focus on what is a feature, how to measure it's importance/sparsity efficiently, and then deal correlation and structure in simpler networks first and try to find a mathematical theory that started making good predictions in larger systems based on those terms. I definitely wouldn't start elsewhere.
- In retrospect, maybe I agree that following one's nose is also very important, but I'd want people to have these toy systems and various insights associated with them in mind. I'd also like to see these theoreticians work with empiricists to find and test ways of measuring quantities which would be the subject of the theorizing.
- "And perhaps there really is something about nature that makes it fundamentally amenable to mathematical description in a way that just won't apply to a large neural network trained by some sort of gradient descent? " I am tempted to take the view that nature is amenable in a very similar way to neural networks, but I believe that nature includes many domains which we can't/don't/struggle to make precise predictions or relations about. Specifically, I used to work in molecular systems biology which I think we understand way better than we used to but just isn't accessible in the way Newtonian physics is. Another example might be ecology where you might be able to predict migrations or other large effects but not specific details about ecosystems like specofic species population numbers more than 6 months in advance (this is totally unqualified conjecture to illustrate a point). So if Neural Networks are amenable to a mathematical description but only to the same extent molecular systems biology then we might be in for a hard time. The only recourse I think we have is to consider that we are have a few advantages with neural networks we don't have in other systems we want to model (see Chris Olahs blog post here https://colah.github.io/notes/interp-v-neuro/).
I should add that part of the value I see in my own work is to create slightly more complicated transformers than those which are studied the MI literature because rather than solving algorithmic tasks they solve spatial tasks based on instructions. These systems are certainly messier and may be a good challenge for a theory of neural network mechanisms/interpretability to make detailed predictions about. I think going straight from toy models to LLMs would be like going from studying viruses/virus replication to ecosystems.
Suggestions for next steps if you agreed with me about the value of existing work and building predictions of small systems first and trying to expand predictions to larger neural networks;
- Publishing/crowdsourcing/curating a literature review of anything that might be required to start building this theory (I'm guessing my knowledge of MI related work is just one small subsection of the relevant work and If I saw it as my job to create a broader theory I'd be reading way more widely.
- Identifying key goals for such a theory such as expanding or identifying quantitaties which such a theory would relate to each other, reliably retropredicting details of previously studied phenomena such as polysemanticity, grokking, memorization, generalization, which features get represented and then also making novel predictions such as about how mechanisms compose in neural networks ( not sure if anyone's published on this yet).
The two phenomena/concepts I am most interested in seeing either good empirical or theoretical work on are:
- Composition of mechanisms in neural networks (analogous to gene regulation). Something like explaining how Bhillal's extends to systems that solve more than one task at once where components can be reused and making predictions about how that gets structured in different architectures and as function of different details of training methods.
- Prediction centralization of processing (eg: the human prefrontal cortex). How when why would such a module arise and possibly how do we avoid it happening in LLMs if it hasn't started happening already.
+1 to making a concerted effort to have a mathematical theory +1 on using the term not killeveryonism
Hey Joseph, thanks for the substantial reply and the questions!
Why call this a theory of interpretability as opposed to a theory of neural networks?
Yeah this is something I am unsure about myself (I wrote: "something that I'm clumsily thinking of as 'the mathematics of (the interpretability of) deep learning-based AI'"). But I think I was imagining that a 'theory of neural networks' would be definitely broader than what I have in mind as being useful for not-kill-everyoneism. I suppose I imagine it including lots of things that are interesting about NNs mathematically or scientifically but which aren't really contributing to our ability to understand and manage the intelligences that NNs give rise to. So I wanted to try to shift the emphasis away from 'understanding NNs' and towards 'interpreting AI'.
But maybe the distinction is more minor than I was originally worried about; I'm not sure.
have you made any progress on this topic or do you know anyone who would describe this explicitly as their research agenda? If so what areas are they working in.
No, I haven't really. It was - and maybe still is - a sort of plan B of mine. I don't know anyone who I would say has this as their research agenda. I think the closest/next best thing people are well known, e.g. the more theoretical parts of Anthropic/Neel's work and more recently the interest in singular learning theory from Jesse Hoogland, Alexander GO, Lucius Bushnaq and maybe others. (afaict there is a belief that it's more than just 'theory of NNs' but can actually tell us something about safety of the AIs)
One thing I struggle to understand, and might bet against is that this won't involve studying toy models. To my mind, Neel's grokking work, Toy Models of Superposition, Bhillal's "A Toy Model of Universality: Reverse Engineering How Networks Learn Group Operations" all seems to be contributing towards important factors that no comprehensive theory of Neural Networks could ignore....
I think maybe I didn't express myself clearly or the analogy I tried to make didn't work as intended, because I think maybe we actually agree here(!). I think one reason I made it confusing is because my default position is more skeptical about MI than a lot of readers probably....so, with regards to the part where I said: "it is reasonable that the early stages of rigorous development don't naively 'look like' the kinds of things we ultimately want to be talking about. This is very relevant to bear in mind when considering things like the mechanistic interpretability of toy models." What I was trying to get at is that to me proving e.g. some mathematical fact about superposition in a toy model doesn't look like the kind of 'intepretability of AI' that you really ultimately want, it looks too low-level. It's a 'toy model' in the NN sense, but its not a toy version of the hard part of the problem. But I was trying to say that you would indeed have to let people like mathematicians actually ask these questions - i.e ask the questions about e.g. superposition that they would most want to know the answers to, rather than forcing them to only do work that obviously showed some connection to the bigger theme of the actual cognition of intelligent agents or whatever.
Thanks for the suggestions about next steps and for writing about what you're most interested in seeing. I think your second suggestion in particular is close to the sort of thing I'd be most interested in doing. But I think in practice, a number of factors have held me back from going down this route myself:
- Main thing holding me back is probably something like: There just currently aren't enough people doing it - no critical mass. Obviously there's that classic game theoretic element here in that plausibly lots of people's minds would be simultaneously changed by there being a critical mass and so if we all dived in at once, it just works out. But it doesn't mean I can solve the issue myself. I would want way more people seriously signed up to doing this stuff including people with more experience than myself (and hopefully the possibility that I would have at least some 'access' to those people/opportunity to learn from them etc.) which seems quite unlikely.
- It's really slow and difficult. I have had the impression talking to some people in the field that they like the sound of this sort of thing but I often feel that they are probably underestimating how slow and incremental it is.
- And a related issue is sort of the existence of jobs/job security/funding to seriously pursue it for a while without worrying too much in the short term about getting concrete results out.
Thanks Spencer! I'd love to respond in detail but alas, I lack the time at the moment.
Some quick points:
- I'm also really excited about SLT work. I'm curious to what degree there's value in looking at toy models (such as Neel's grokking work) and exploring them via SLT or to what extent reasoning in SLT might be reinvigorated by integrating experimental ideas/methodology from MI (such as progress measures). It feels plausible to me that there just haven't been enough people in any of a number of intersections look at stuff and this is a good example. Not sure if you're planning on going to this: https://www.lesswrong.com/posts/HtxLbGvD7htCybLmZ/singularities-against-the-singularity-announcing-workshop-on but it's probably not in the cards for me. I'm wondering if promoting it to people with MI experience could be good.
- I totally get what you're saying about toy model in sense A or B doesn't necessarily equate to a toy model being a version of the hard part of the problem. This explanation helped a lot, thank you!
- I hear what you are saying about next steps being challenging for logistical and coordination issues and because the problem is just really hard! I guess the recourse we have is something like: Look for opportunities/chances that might justify giving something like this more attention or coordination. I'm also wondering if there might be ways of dramatically lowering the bar for doing work in related areas (eg: the same way Neel writing TransformerLens got a lot more people into MI).
Looking forward to more discussions on this in the future, all the best!
If the trajectory of the deep learning paradigm continues, it seems plausible to me that in order for applications of low-level interpretability to AI not-kill-everyone-ism to be truly reliable, we will need a much better-developed and more general theoretical and mathematical framework for deep learning than currently exists. And this sort of work seems difficult. Doing mathematics carefully - in particular finding correct, rigorous statements and then finding correct proofs of those statements - is slow. So slow that the rate of change of cutting-edge engineering practices significantly worsens the difficulties involved in building theory at the right level of generality. And, in my opinion, much slower than the rate at which we can generate informal observations that might possibly be worthy of further mathematical investigation. Thus it can feel like the role that serious mathematics has to play in interpretability is primarily reactive, i.e. consists mostly of activities like 'adding' rigour after the fact or building narrow models to explain specific already-observed phenomena.
My impression however, is that the best applied mathematics doesn’t tend to work like this. My impression is that although the use of mathematics in a given field may initially be reactive and disunited, one of the most lauded aspects of mathematics is a certain inevitability with which our abstractions take on a life of their own and reward us later with insight, generalization, and the provision of predictions. Moreover - remarkably - often those abstractions are found in relatively mysterious, intuitive ways: i.e. not as the result of us just directly asking "What kind of thing seems most useful for understanding this object and making predictions?" but, at least in part, as a result of aesthetic judgement and a sense of mathematical taste. One consequence of this (which is a downside and also probably partly due to the inherent limitations of human mathematics) is that mathematics does not tend to act as an objective tool that you can bring to bear on whatever question it is that you want to think about. Instead, the very practice of doing mathematics seeks out the questions that mathematics is best placed to answer. It cannot be used to say something useful about just anything; rather it finds out what it is that it can say something about.
Even after taking into account these limitations and reservations, developing something that I'm clumsily thinking of as 'the mathematics of (the interpretability of) deep learning-based AI' might still be a fruitful endeavour. In case it is not clear, this is roughly speaking, because a) Many people are putting a lot of hope and resources into low-level interpretability; b) Its biggest hurdles will be making it 'work' at large scale, on large models, quickly and reliably; and c) - the sentiment I opened this article with - doing this latter thing might well require much more sophisticated general theory.
In thinking about some of these themes, I started to mull over a couple of illustrative analogies or examples. The first - and more substantive example - is algebraic topology. This area of mathematics concerns itself with certain ways of assigning mathematical (specifically algebraic) information to shapes and spaces. Many of its foundational ideas have beautiful informal intuitions behind them, such as the notion that a shape my have enough space in it to contain a sphere, but not enough space to contain the ball that that sphere might have demarcated. Developing these informal notions into rigorous mathematics was a long and difficult process and learning this material - even now when it is presented in its best form - is laborious. The mathematical details themselves do not seem beautiful or geometric or intuitive; and it is a slow and alienating process. One has to begin by working with very low-level concrete details - such as how to define the boundary of a triangle in a way that respects the ordering of the vertices - details that can sometimes seem far removed from the type of higher-level concepts that one was originally trying to capture and say something about. But once one has done the hard work of carefully building up the rigorous theory and internalizing its details, the pay-off can be extreme. Your vista opens back up and you are rewarded with very flexible and powerful ways of thinking (in this case about potentially very complicated higher-dimensional shapes and spaces). Readers may recognize this general story as a case of Terry Tao's now very well-known "three stages" of mathematical education, just applied specifically to algebraic topology. I additionally want to point out that within pure mathematics, algebraic topology often has an applicable and computational flavour too, in the sense that there is something like a toolkit of methods from algebraic topology that one can bring to bear on previously unseen spaces and shapes in order to get information about them. So, to try to summarize and map this story onto the interpretability of deep learning-based AI, some of my impressions are that:
The second illustrative example that I have in mind is mathematical physics. This isn't a subject that I know a lot about and so it's perfectly possible that I end up misrepresenting things here, but essentially it is the prototypical example of the kind of thing I am getting at. In very simplified terms, successes of mathematical physics might be said to follow a pattern in which informal and empirically-grounded thinking eventually results in the construction of sophisticated theoretical and mathematical frameworks, which in turn leads to the phase in which the cycle completes and the mathematics of those frameworks provide real-world insights and predictions. Moreover, this latter stage often doesn't look like stating and proving theorems, but rather 'playing around' with the appropriate mathematical objects at just the right level of rigour, often using them over and over again in computations (in the pure math sense of the word) pertaining to specific examples. One can imagine wishing that something like this might play out or 'the mathematics of interpretability'.
Perhaps the most celebrated set of examples of this kind of thing are from the representation theory of Lie groups. Again, I know little about the physics so will avoid going into detail but the relevant point here is that the true descriptive, explanatory and predictive relevance of something like the representation theory of Lie groups was not unlocked by physicists alone. The theory only became quite so highly-developed because a large community of 'pure' mathematicians pursuing all sorts of related questions to do with smooth manifolds, groups, representation theory in general etc. helped to mature the area.
One (perhaps relatively unimportant) difference between this story and the one we want to tell for AI not-kill-everyone-ism is that the typical mathematician studying, say, representation theory in this story might well have been doing so for mostly 'pure' mathematical reasons (and not because they thought their work might one day be part of a framework that predicts the behaviour of fundamental forces or something), whereas we are suggesting developing mathematical theory while remaining guided by the eventual application to AI. A more important difference - and a more genuine criticism of this analogy - is that mathematical physics is of course applied to the real, natural world. And perhaps there really is something about nature that makes it fundamentally amenable to mathematical description in a way that just won't apply to a large neural network trained by some sort of gradient descent? Indeed one does have the feeling that the endeavour we are focussing on would have to be underpinned by a hope that there is something sufficiently 'natural' about deep learning systems that will ultimately make at least some higher-level aspects of them amenable to mathematical analysis. Right now I cannot say how big of a problem this is.
I will try to sum up:
I'm very interested in comments and thoughts.