I've been thinking recently about how to teach the Pythagorean theorem to high school students. As part of that thinking, I looked around to see how the topic was being taught in various textbooks, online videos, blog posts, etc. Typically, the discussion goes something like this:

First, the statement of the theorem is presented: For a right triangle with legs of lengths $a$ and $b$ and a hypotenuse of length $c$, we have $a^2+b^2=c^2$.

Next, a picture like the following one is presented as a visual:
 

The student is told that the two smaller squares add up in area to the largest square.

Finally, any one of the typical proofs is presented. This could be a rearrangement proof, the "Behold!" proof, or Euclid's proof of proposition I.47.

One can improve the final step by using what is sometimes called Einstein's proof. (See also this post by Terence Tao, this video by Numberphile, this article by Alexander Givental, and in particular this comment by Tim Gowers for discussion and presentation of this proof.) This proof is an improvement over the typical presentation for a few reasons: it makes the theorem feel more intuitive, and (especially with the discussion in Gowers's comment) it gives some indication of how one might discover the proof.

It might seem like the "exposition problem" for the Pythagorean theorem is solved: we started with a bunch of proofs that made the theorem feel unintuitive that we didn't know how to discover ourselves, and now we have a good proof along with a story for how to discover it.

I claim that there is still some work left! I think the Pythagorean theorem is a case where even the theorem statement itself seems bizarre (rather than just the proofs being bizarre). Given an arbitrary right triangle, how would one guess that $a^2+b^2=c^2$? And why would one even think this is a problem worth solving in the first place? I think this second question is easy to answer by pointing to the numerous applications of the theorem, so I will focus on the first question.

So with that background discussion out of the way, here is my proposal for how to teach the Pythagorean theorem, which is a kind of discovery fiction:

• Present the problem: this can be either finding the length of a vector/line segment in the Cartesian plane (given the $x$ and $y$ coordinates), or as finding the hypotenuse of a right triangle (given the lengths of the two legs). It is clear that once $x$ and $y$ are known, the length of the hypotenuse is determined. (Ideally if this was an in-person lesson, I would present the problem, then let the student just think about it on their own. Then parts of the lesson might just be discussing about whatever idea the student had/altering some of the approach based on ideas of the student.)
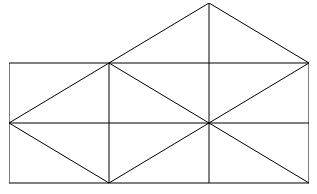
• Eventually, hit on the idea of specializing/simplifying the problem by taking the two legs to be the same length. In this case, it becomes really obvious (by drawing the picture) that the "bigger square" made using the diagonal of the original square is double the area of the original square. This opens up two interesting threads: (1) it shows that the length of the diagonal of the original square is $\sqrt{2}$, and this then could lead to a lesson on its own about irrational numbers; (2) it gives an idea of how to generalize this approach to the case where the legs don't have the same length.

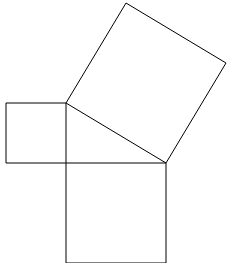
• Attempt to generalize to the case where the legs have different lengths: Try to make the same drawing as in the square case. This will fail: the legs will have rectangles attached, and the hypotenuse will have a rhombus attached. There will be no obvious way to find the height of this rhombus, so no way to connect the area of the rhombus to the hypotenuse of the original triangle.

• Think more about why the rectangle one fails even though the square one works. Hit on the idea that it works in the square case because the hypotenuse goes on to create a square, whose area we can calculate in terms of the hypotenuse. In contrast, in the rhombus case, there is no obvious way to calculate the area using the hypotenuse (in fact, the typical formula for the area of the rhombus calculates it in terms of the diagonals, which gives the tautologous $2ab=2ab$). So the question now becomes: is there a way to draw the figure in such a way that the hypotenuse creates (i.e. has attached) a figure whose area we can calculate using the hypotenuse itself?
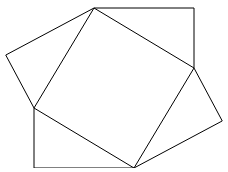
• One way is to grow a square on the hypotenuse; but doing this just any way won't work. Possibly after a few attempts, you will discover that putting the smallest angle in the right triangle along with the next smallest angle creates a straight line, with a right angle in between. This can be used to surround the square (with hypotenuse as the side length), creating an outer square of length $a+b$. This soon leads to the familiar formula, $c^2=a^2+b^2$ (after some algebra). This is of course "just" the "Behold!" proof, but it is now preceded by a story consisting of a bunch of motivated exploration.

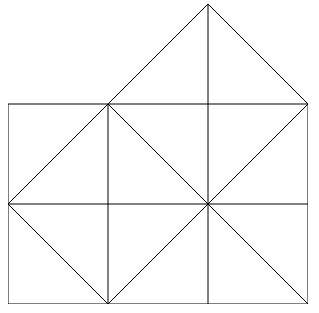
• I think the previous proof is probably easier to find, but it's not the most intuitive explanation. So another way to think about this is, we didn't need a square; we just needed some area that we could calculate using the hypotenuse. But actually, something to notice is that we don't even necessarily need to calculate it. Once we know the theorem statement, any three similar figures would work. So we can (1) generalize the Pythagorean theorem to be about any shape, and (2) try to specialize to some shape that is especially easy to work with. This is of course just the same idea Gowers discusses from Polya's book.
• Eventually the above idea leads to drawing a perpendicular line down to the hypotenuse, which creates three similar triangles. The areas of the two smaller triangles obviously adds up to the area of the largest triangle, so we have $A+B=C$. Then, we just note that for similar figures, area is proportional to the square of the side lengths, so we must have $a^2+b^2=c^2$.

Here are some things I like about this proposal:

• It makes use of problem-solving strategies like specialization and generalization.
• Not only the proof, but the theorem statement itself is part of the discovery process.
• It teaches that once the theorem is known, other more intuitive proofs can be found. The first proof is not necessarily the best proof. But the first proof is still historically necessary for discovering the better proof.
• It gives some feel for the "combinatorial explosion" nature of math research: we started out talking about right triangles, but then discovered $\sqrt{2}$, something we weren't even trying to do.

Here are some questions I am wondering about, and I am interested in hearing people's thoughts:

• How convincing was the above as an explanation? Which parts were difficult to follow?
• Can I really expect most high school students to follow through on this lesson? Is there anything that is too conceptually difficult?
• I think there's a lot of value to having the student figure things out on their own, so what is the minimal amount of hand-holding I can get away with? I know I can't just present the problem and expect even the smartest students to figure everything out, but I also don't want to give away all of the answers, and I am having trouble figuring out what the right balance is.
• Are there other compelling "discovery paths" that I am missing?