Summary
Agents might fail to peacefully trade in high-stakes negotiations. Such bargaining failures can have catastrophic consequences, including great power conflicts, and AI flash wars. This post is a distillation of DiGiovanni et al. (2024) (DCM), whose central result is that agents that are sufficiently transparent to each other have individual incentives to avoid catastrophic bargaining failures. More precisely, DCM constructs strategies that are plausibly individually incentivized, and, if adopted by all, guarantee each player no less than their least preferred trade outcome. Figure 0 below illustrates this.

This result is significant because artificial general intelligences (AGIs) might (i) be involved in high-stakes negotiations, (ii) be designed with the capabilities required for the type of strategy we’ll present, and (iii) bargain poorly by default (since bargaining competence isn’t necessarily a direct corollary of intelligence-relevant capabilities).
Introduction
Early AGIs might fail to make compatible demands with each other in high-stakes negotiations (we call this a “bargaining failure”). Bargaining failures can have catastrophic consequences, including great power conflicts, or AI triggering a flash war. More generally, a “bargaining problem” is when multiple agents need to determine how to divide value among themselves.
Early AGIs might possess insufficient bargaining skills because intelligence-relevant capabilities don’t necessarily imply these skills: For instance, being skilled at avoiding bargaining failures might not be necessary for taking over. Another problem is that there might be no single rational way to act in a given multi-agent interaction. Even arbitrarily capable agents might have different priors, or different approaches to reasoning under bounded computation. Therefore they might fail to solve equilibrium selection, i.e., make incompatible demands (see Stastny et al. (2021) and Conitzer & Oesterheld (2023)). What, then, are sufficient conditions for agents to avoid catastrophic bargaining failures?
Sufficiently advanced AIs might be able to verify each other’s decision algorithms (e.g. via verifying source code), as studied in open-source game theory. This has both potential downsides and upsides for bargaining problems. On one hand, transparency of decision algorithms might make aggressive commitments more credible and thus more attractive (see Sec. 5.2 of Dafoe et al. (2020) for discussion). On the other hand, agents might be able to mitigate bargaining failures by verifying cooperative commitments.
Oesterheld & Conitzer (2022)’s safe Pareto improvements[1] (SPI) leverages transparency to reduce the downsides of incompatible commitments. In an SPI, agents conditionally commit to change how they play a game relative to some default such that everyone is (weakly) better off than the default with certainty.[2] For example, two parties A and B who would otherwise go to war over some territory might commit to, instead, accept the outcome of a lottery that allocates the territory to A with the probability that A would have won the war (assuming this probability is common knowledge). See also our extended example below.
Oesterheld & Conitzer (2022) has two important limitations: First, many different SPIs are in general possible, such that there is an “SPI selection problem”, similar to the equilibrium selection problem in game theory (Sec. 6 of Oesterheld & Conitzer (2022)). And if players don’t coordinate on which SPI to implement, they might fail to avoid conflict.[3] Second, if expected utility-maximizing agents need to individually adopt strategies to implement an SPI, it’s unclear what conditions on their beliefs guarantee that they have individual incentives to adopt those strategies.
So, when do expected utility-maximizing agents have individual incentives to implement mutually compatible SPIs? And to what extent are inefficiencies reduced as a result? These are the questions that we focus on here. Our main result is the construction of strategies that (1) are individually incentivized and (2) guarantee an upper bound on potential utility losses from bargaining failures without requiring coordination, under conditions spelled out later. This bound guarantees that especially bad conflict outcomes — i.e., outcomes that are worse for all players than any Pareto-efficient outcome — will be avoided when each agent chooses a strategy that is individually optimal given their beliefs. Thus, e.g., in mutually assured destruction, if both parties prefer yielding to any demand over total annihilation, then such annihilation will be avoided.
Importantly, our result:
- Applies to agents who individually optimize their utility functions;[4]
- does not require them to coordinate on a specific bargaining solution;
- places few requirements on their beliefs; and
holds for any game of complete information (i.e., where the agents know the utilities of each possible outcome for all agents, and all of each other’s possible strategies). That said, we believe extending our results to games of incomplete information is straightforward.[5]
Our result does however require:
- Simultaneous commitments: Agents commit independently of each other to their respective strategies;[6],[7]
- Perfect credibility: It is common knowledge that any strategy an agent commits to is credible to all others — for instance because agents can see each other’s source code;
Mild assumptions on players’ beliefs.[8]
The Pareto meet minimum bound
What exactly is the bound we’ll put on utility losses from bargaining failures? Brief background: For any game, consider the set of outcomes where each player’s payoff is at least as good as their least-preferred Pareto-efficient outcome — Rabin (1994) calls this set the Pareto meet. (See the top-right triangle in the figure below, which depicts the payoffs of a generic two-player game.) The Pareto meet minimum (PMM) is the Pareto-worst payoff tuple in the Pareto meet.

Our central claim is that agents will, under the assumptions stated in the previous section, achieve at least as much utility as their payoff under the PMM. The bound is tight: For some possible beliefs satisfying our assumptions, players with those beliefs are not incentivized to use strategies that guarantee strictly more than the PMM. Our proof is constructive: For any given player and any strategy this player might consider adopting, we construct a modified strategy such that 1) the player weakly prefers to unilaterally switch to the modified strategy, and 2) when all players modify their strategies in this way, they achieve a Pareto improvement guaranteeing at least the PMM. In other words, we construct an individually incentivized SPI as defined above.
Related work
Rabin (1994) and Santos (2000) showed that players in bargaining problems are guaranteed their PMM payoffs in equilibrium, i.e., assuming players know each other’s strategies exactly (which our result doesn’t assume). The PMM is related to Yudkowsky’s / Armstrong’s (2013) proposal for bargaining between agents with different notions of fairness.[9] While Yudkowsky (2013) similarly presents a joint procedure that guarantees players the PMM when they all use it, he does not prove (as we do) that under certain conditions players each individually prefer to opt in to this procedure.
In the rest of the post, we first give an informal intuition for the PMM bound, and then move on to proving it more rigorously.
Intuition for the PMM bound
The Costly War game. The nations of Aliceland and Bobbesia[10] are to divide between them a contested territory for a potential profit of 100 utils. Any split of the territory’s value is possible. If the players come to an agreement, they divide the territory based on their agreement; if they fail to agree, they wage a costly war over the territory, which costs each of them 50 utils in expectation. Fig. 2 represents this game graphically:[11]
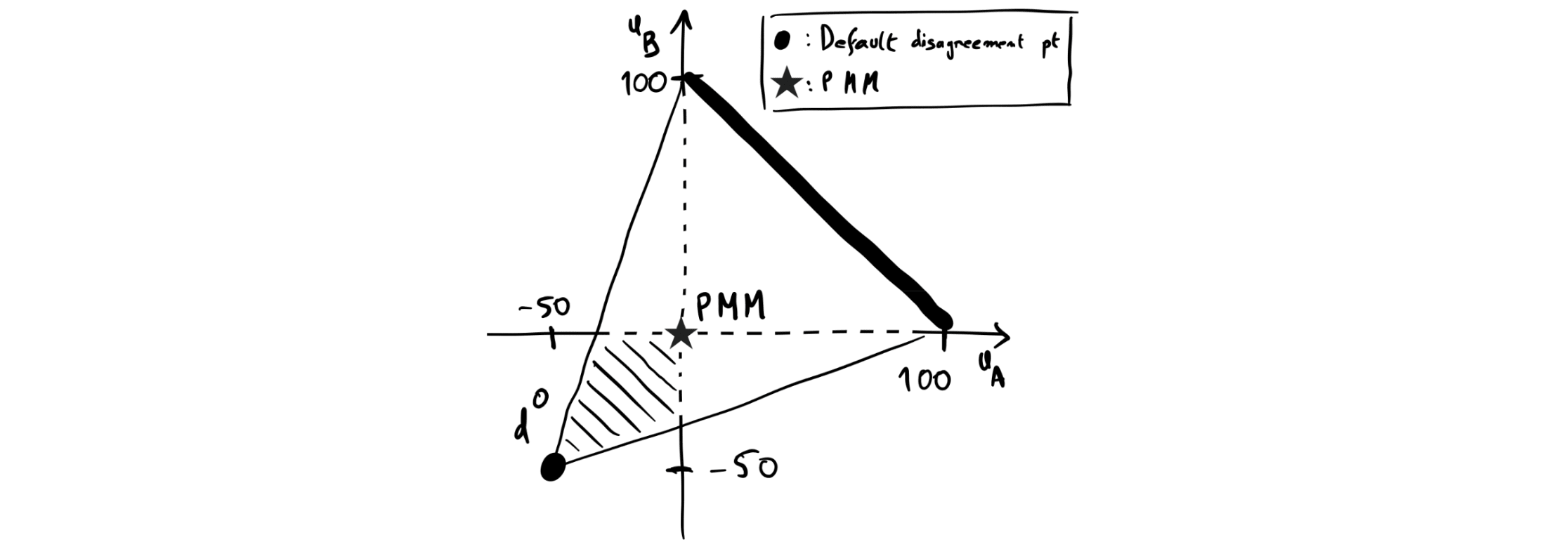
Assume communication lines are closed prior to bargaining (perhaps to prevent spying), such that each player commits to a bargaining strategy in ignorance of their counterpart’s strategy.[12] Players might then make incompatible commitments leading to war. For instance, Aliceland might believe that Bobbesia is very likely to commit to a bargaining strategy that only concedes to an aggressive commitment of the type, C = “I [Aliceland] get all of the territory, or we wage a costly war”, such that it is optimal for Aliceland to commit to C. If Bobbesia has symmetric beliefs, they’ll fail to agree on a deal and war will ensue.[13]
To mitigate those potential bargaining failures, both nations have agreed to play a modified version of the Costly War game. (This assumption of agreement to a modified game is just for the sake of intuition — our main result follows from players unilaterally adopting certain strategies.) This modification is as follows:
- Call the original game . Each player independently commits to replacing the disagreement point with a Pareto-better outcome , conditional on the counterpart choosing the same . Call this new game .
- Each player independently commits to a bargaining strategy that will be played regardless of whether the bargaining game is or .
- (As we’ll see later, the following weaker assumption is sufficient for the PMM result to hold: Aliceland bargains equivalently in both games, but she only agrees to play if Bobbesia also bargains equivalently. Moreover, she believes that whenever Bobbesia doesn’t bargain equivalently, he bargains in exactly like he would have if Aliceland hadn’t proposed a Pareto-better disagreement point. (And the same holds with the role of both players exchanged.))
Now we’ll justify the claims that 1) the PMM bound holds, and 2) this bound is tight.
The PMM bound holds
That is, players have individual incentives to propose the PMM or Pareto-better as the disagreement point. To see why that holds, fix a in the shaded region, and fix a pair of strategies for Aliceland and Bobbesia. Then either:
- They bargain successfully, and using rather than d doesn’t change anything; or
- Bargaining fails, and both players are better off using rather than .
Thus, a in the shaded region improves the payoff of bargaining failure for both parties without interfering with the bargaining itself (because they play the same strategy in and ). Since the PMM is the unique Pareto-efficient point among points in the shaded region, it seems implausible for a player to believe that their counterpart will propose a disagreement point Pareto-worse than the PMM.
The PMM bound is tight
Why do the players not just avoid conflict entirely and go to the Pareto frontier? Let’s construct plausible beliefs under which Aliceland is not incentivized to propose a point strictly better than the PMM for Bobbesia:
- Suppose Aliceland thinks Bobbesia will almost certainly propose her best outcome as the disagreement point.
- Why would Bobbesia do this? Informally, this could be because he thinks that if he commits to an aggressive bargaining policy, (i) he is likely to successfully trade and get his best outcome and (ii) whenever he fails to successfully trade, Aliceland is likely to have picked her best outcome as the disagreement point. This is analogous to why Bobbesia might concede to an aggressive bargaining strategy, as discussed above.
Then, she thinks that her optimal play is to also propose her best outcome as the disagreement point (and to bargain in a way that rejects any outcome that isn’t her preferred outcome). Thus, the bound is tight.[14]
Does this result generalize to all simultaneous-move bargaining games, including games with more than two players? And can we address the coordination problem of players aiming for different replacement disagreement points (both Pareto-better than the PMM)? As it turns out, the answer to all of this is yes! This is shown in the next section, where we prove the PMM bound more rigorously using the more general framework of program games.
The PMM bound: In-depth
In this section, we first introduce the standard framework for open-source game theory, program games. Then we use this framework to construct strategies that achieve at least the PMM against each other, and show that players are individually incentivized to use those strategies.
Program games
Consider some arbitrary “base game,” such as Costly War. Importantly, we make no assumptions about the structure of the game itself: It can be a complex sequential game (like a game of chess, or a non-zero sum game like iterated Chicken or Rubinstein bargaining).[15] We’ll for simplicity discuss the case of two players in the main text, and the general case in appendix. We assume complete information. Let denote the utility function of player , which maps action tuples (hereafter, profiles) to payoffs, i.e., tells us how much each player values each outcome.[16]
Then, a program game (Tennenholtz (2004)) is a meta-game built on top of the base game, where each player’s strategy is a choice of program. Program games can be seen as a formal description of open-source games, i.e., scenarios where highly transparent agents interact. A program is a function that takes as input the source code of the counterpart’s program, and outputs an action in the base game (that is, a program is a conditional commitment).[17] For instance, in the Prisoner’s Dilemma, one possible program is CliqueBot (McAfee (1984), Tennenholtz (2004), Barasz et al. (2014)), which cooperates if the counterpart’s source code is CliqueBot’s source code, and defects otherwise.
We’ll assume that for any program profile programs in terminate against each other.[18] With that assumption, a well-defined outcome is associated to each program profile.
As a concrete example, consider the following program game on Prisoner’s Dilemma, where each player can choose between “CooperateBot” (a program that always cooperates), “DefectBot” (always defects), and CliqueBot:
| CooperateBot | DefectBot | CliqueBot | |
| CooperateBot | 2,2 | 0,3 | 0,3 |
| DefectBot | 3,0 | 1,1 | 1,1 |
| CliqueBot | 3,0 | 1,1 | 2,2 |
The light shaded submatrix is the matrix of the base game, whose unique Nash equilibrium is mutual defection for 1 util. Adding CliqueBot enlarges the game matrix, and adds a second Nash equilibrium (dark shaded), where each player chooses CliqueBot and cooperates for 2 utils.
Renegotiation programs
What does the program game framework buy us, besides generality? We don’t want to assume, as in the Costly War example, that players agree to some modified way of playing a game. Instead, we want to show that each player prefers to use a type of conditional commitment that achieves the PMM or Pareto-better if everyone uses it. (This is analogous to how, in a program game of the Prisoner’s Dilemma, each individual player (weakly) prefers to use CliqueBot instead of DefectBot.)
To do this, we’ll construct a class of programs called renegotiation programs, gradually adding several modifications to a simplified algorithm in order to illustrate why each piece of the final algorithm is necessary. We’ll show how any program profile can be transformed into a renegotiation program profile that achieves the PMM (or Pareto-better). Then we’ll prove that, under weak assumptions on each player’s beliefs, the players individually prefer to transform their own programs in that way.
First, let’s rewrite strategies in the Costly War example as programs. Recall that, to mitigate bargaining failures, each player proposes a new disagreement point (call it ), and commits to a “default” bargaining strategy (call it ). (It will soon become clear why we refer to this strategy as the “default” one.) Then, a program representing a Costly War strategy is identified by a choice of and by a subroutine . We may write in pseudocode:
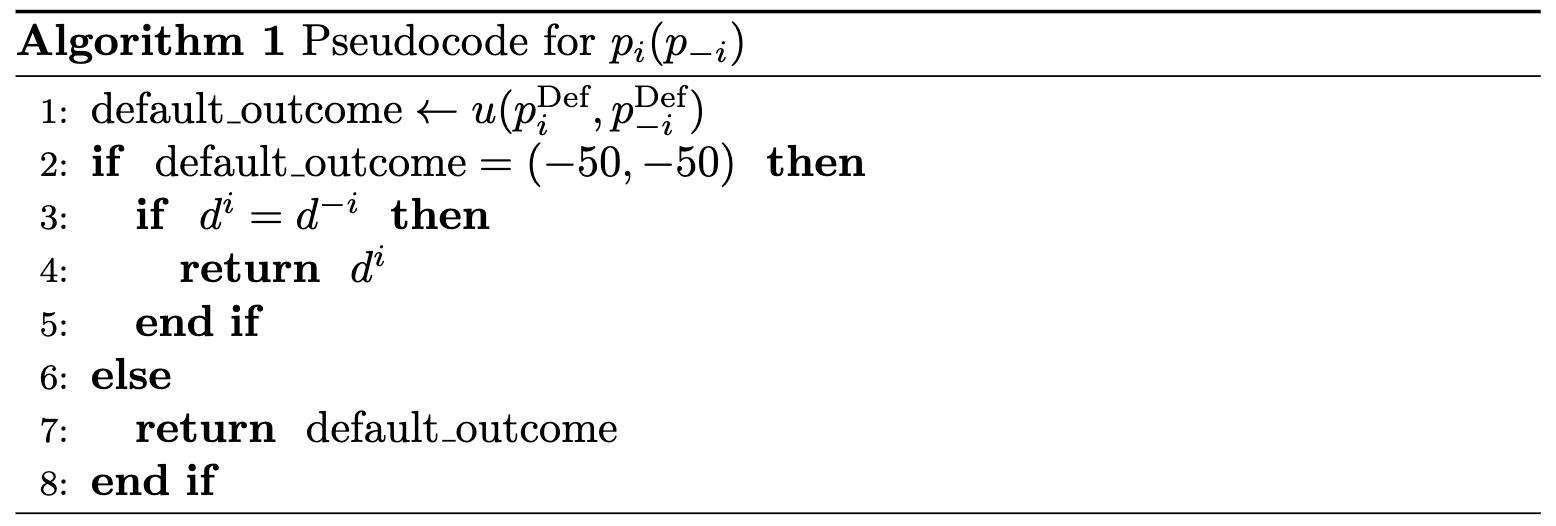
At a high level, the above program tries to renegotiate with the counterpart to improve on the default outcome, if the default is catastrophically bad.[19]
Set-valued renegotiation
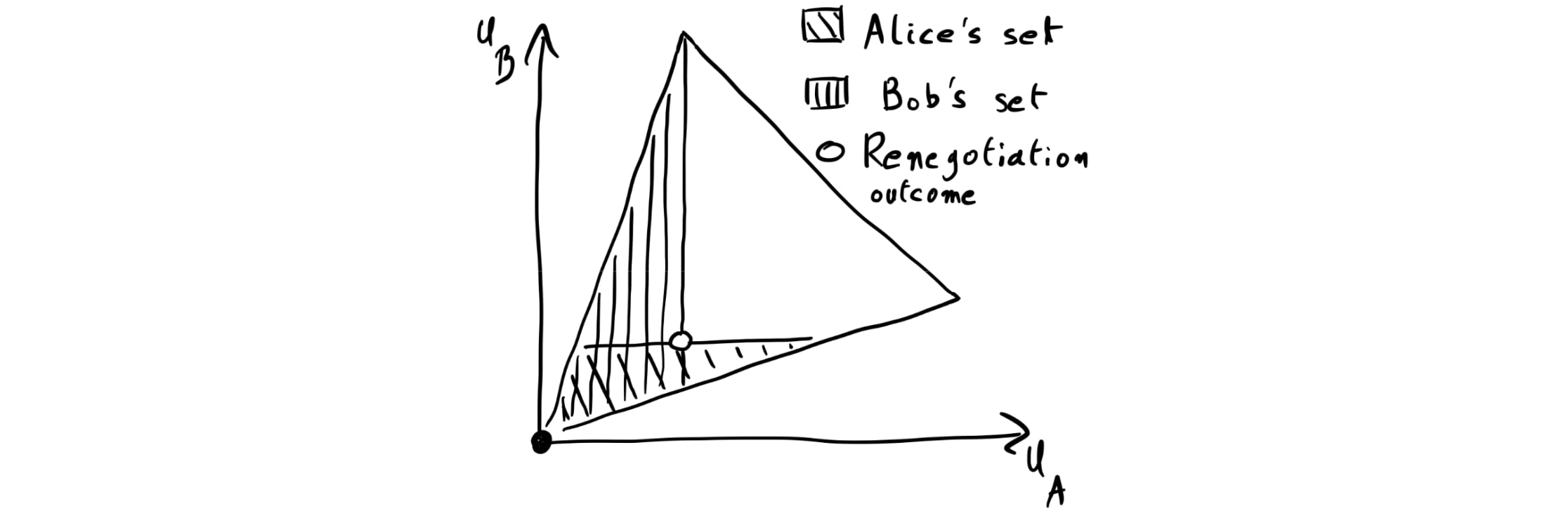
A natural approach to guaranteeing the PMM would be for players to use renegotiation programs that propose the PMM as a renegotiation outcome. But what if the players still choose different renegotiation outcomes that are Pareto-better than the PMM? To address this problem, we now allow each player to propose a set of renegotiation outcomes.[20] (For example, in Fig. 3 below, each player chooses a set of the form “all outcomes where the other player’s payoff is no higher than u,” for some u.) Then, players renegotiate to an outcome that is Pareto-efficient among the outcomes that all their sets contain.
More precisely:
- Let be the outcome players would have obtained by default: .
- Each player submits a renegotiation set .
- (We let the renegotiation set depend on because the renegotiation outcomes must be Pareto improvements on the default.)
- Let the agreement set be the intersection of all players’ renegotiation sets:
- If the sets have a non-empty intersection, then players agree on the outcome , where is a selection function: a function that maps a set of outcomes to a Pareto-efficient outcome in this set.
- Why can we assume the players agree on ? Because all selection functions are equally “expressive,” in the following sense: For any outcome, there is a renegotiation function profile that realizes that outcome under any given selection function. So we can assume players expect the same distribution of outcomes no matter which selection function is used, and hence are indifferent between selection functions. (Analogously, it seems plausible that players will expect their counterparts to bargain equivalently, regardless of which particular formal language everyone agrees to write their programs in.) See appendix for more.
In pseudocode:

Fig. 3 depicts an example of set-valued renegotiation graphically:
Conditional set-valued renegotiation
Set-valued renegotiation as defined doesn’t in general guarantee the PMM. To see this, suppose Alice considers playing the renegotiation set depicted in both plots in Fig. 4 below. If she does that, then Bob will get less than his PMM payoff in either of the two cases. Can we fix that by adding the PMM to Alice’s set? Unfortunately not: If Bob plays the renegotiation set in the right plot of Fig. 4, she is strictly worse off adding the PMM if the selection function chooses the PMM. Therefore, she doesn’t always have an incentive to do that.
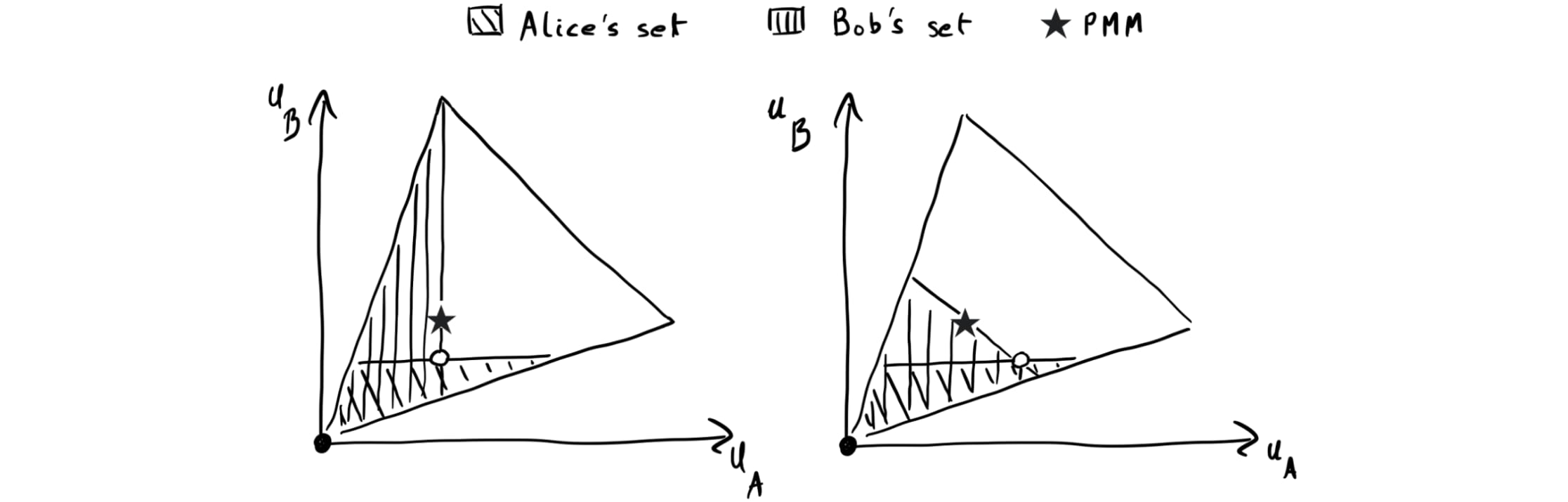
To address the above problem, we let each player choose a renegotiation set conditional on how their counterpart chooses theirs. That is, we allow each renegotiation function to take as input both the counterpart’s renegotiation function and the default outcome , which we write as . We’ll hereafter consider set-valued renegotiation programs with replaced by . (See Algorithm 2 in DCM.) DCM refer to these programs as conditional set-valued renegotiation programs. For simplicity, we'll just say “renegotiation program” hereafter, with the understanding that renegotiation programs need to use conditional renegotiation sets to guarantee the PMM.
Our result will require that all programs can be represented as renegotiation programs. This holds under the following assumption: Roughly, if a program isn’t a renegotiation program, then it responds identically to a renegotiation program as to its default . (This is plausible because and respond identically to .)[21] Given this assumption, any program is equivalent to a renegotiation program with a default program equal to and a renegotiation function that always returns the empty set.
To see how using conditional renegotiation sets helps, let’s introduce one last ingredient, Pareto meet projections.
Pareto meet projections (PMP)
For a given player and any feasible payoff , we define the PMP of for player , denoted , as follows: maps any outcome to the set of Pareto improvements on such that, first, each player’s payoff is at least the PMM, and second, the payoff of the counterpart is not increased except up to the PMM.[22] This definition is perhaps best understood visually:
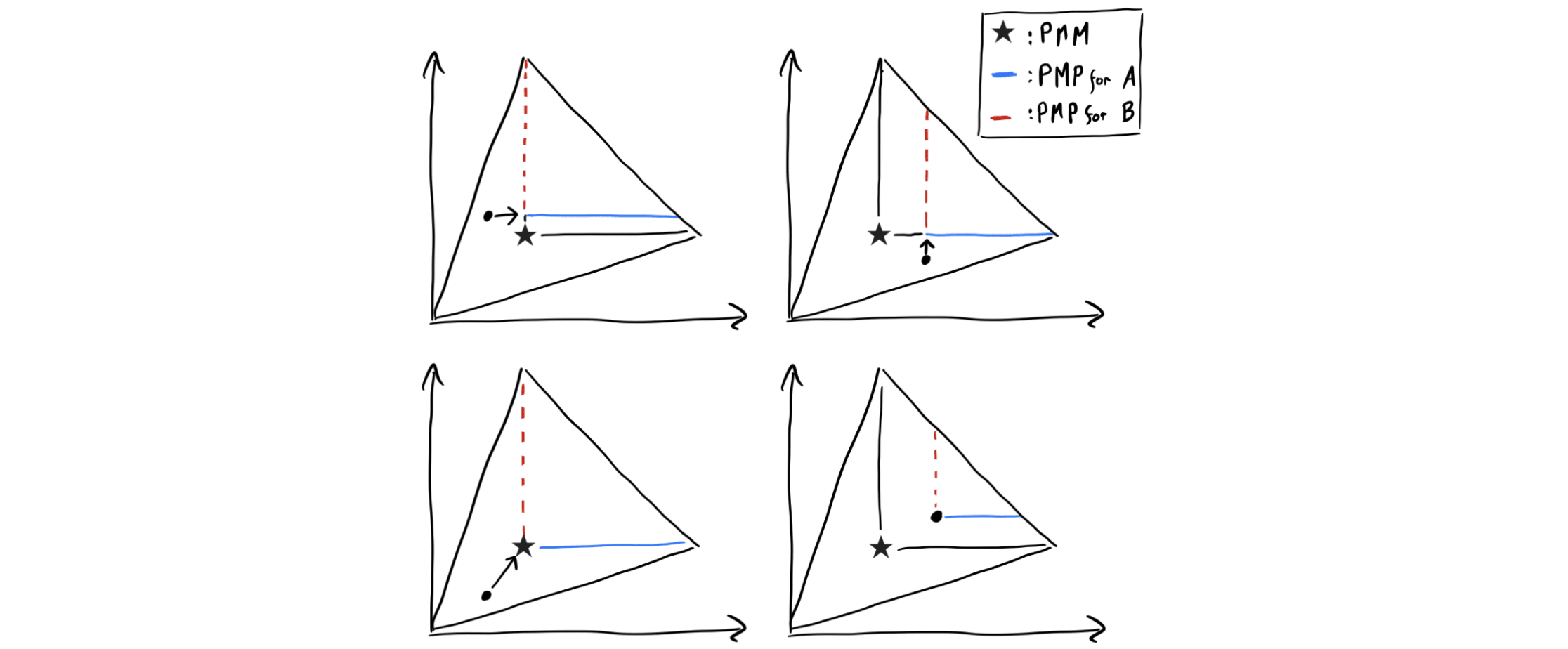
Given a profile of some renegotiation programs the players consider using by default, call the outcome that would be obtained by that profile the default renegotiation outcome. For a renegotiation set returned by a renegotiation function for a given input, we’ll say that a player PMP-extends that set if they add to this set their PMP of the default renegotiation outcome. (Since the default renegotiation outcome of course depends on the other player’s program, this is why conditional renegotiation sets are necessary.) The PMP-extension of a program is the new program whose renegotiation functions return the PMP-extended version of the set returned by the original program, for each possible input. Fig. 6 below illustrates this graphically: On both panels, the empty circle is the default renegotiation outcome, and the blue and dotted red lines are Alice’s and Bob’s PMPs, respectively.
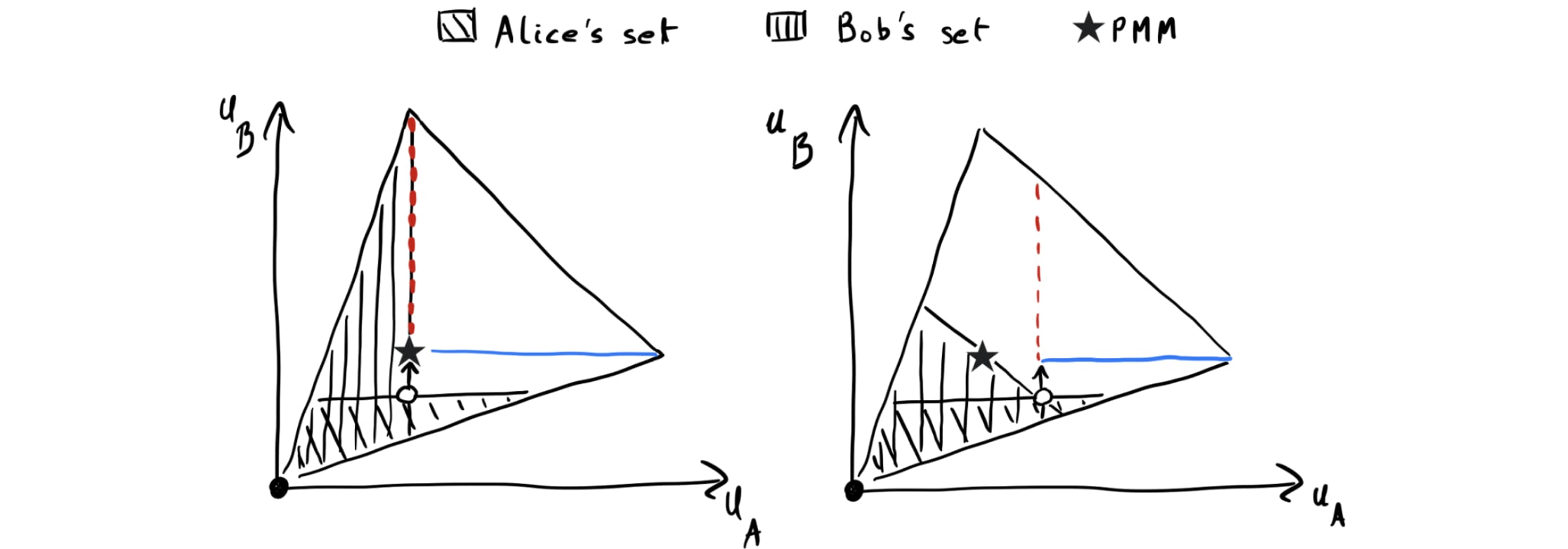
How does PMP-extension help players achieve the PMM or better? The argument here generalizes the argument we gave for the case of Aliceland and Bobbesia in “Intuition for the PMM bound”:
- As illustrated in Fig. 6 below, Alice adding her PMP never makes her worse off, provided that Bob responds at least as favorably to Alice if she adds the PMP than if she doesn’t, i.e. provided that Bob doesn’t punish Alice. And Bob has no incentive to punish Alice, since, for any fixed renegotiation set of Bob, Alice PMP-extending her set doesn’t add any outcomes that are strictly better for Bob yet worse for Alice than the default renegotiation outcome.
And why only add the PMP, rather than a larger set?[23] If Alice were to also add some outcome strictly better for Bob than her PMP, then Bob would have an incentive to change his renegotiation set to guarantee that outcome — which makes Alice worse off than if her most-preferred outcome in her PMP-extension obtained. (That is, in this case, the non-punishment assumption discussed in the previous bullet point would not make sense.) Fig. 7 illustrates this.
- You might see where this is going: By a symmetric argument, Bob is never worse off PMP-extending his renegotiation set (adding the red dotted line in Fig. 6), assuming Alice doesn’t punish him for doing so. And if both Bob and Alice add their PMP, they are guaranteed the PMM (left plot of Fig. 6) or Pareto-better (second plot of Fig. 6).
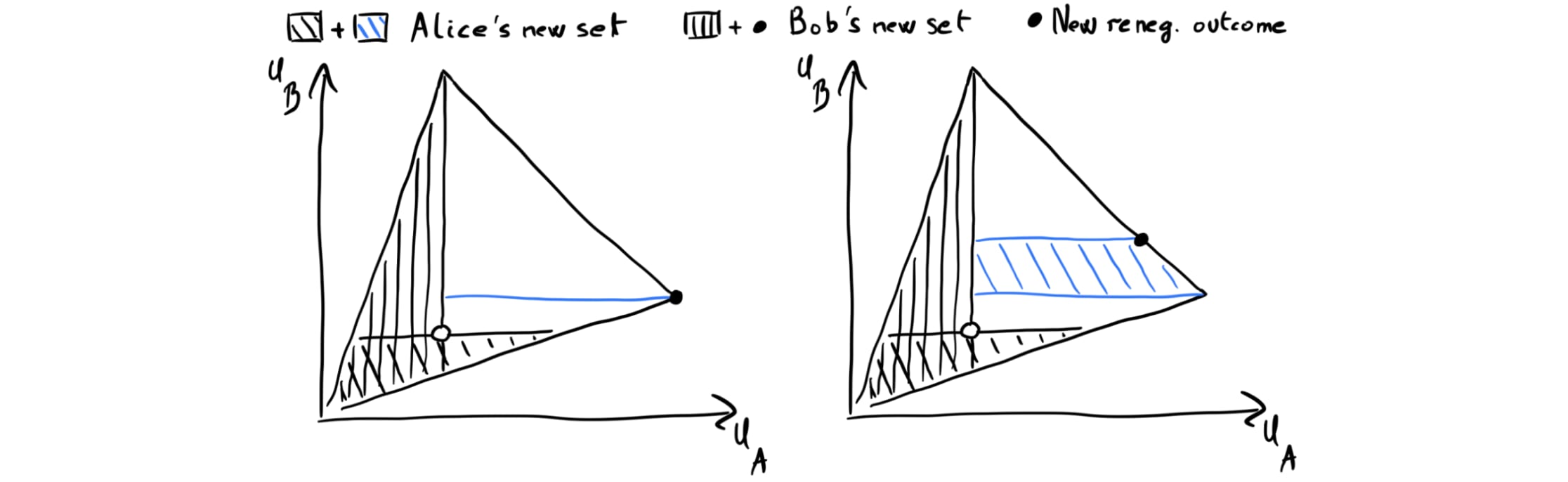
Notice that our argument doesn’t require that players refrain from using programs that implement other kinds of SPIs, besides PMP-extensions.
First, the PMP-extension can be constructed from any default program, including, e.g., a renegotiation program whose renegotiation set is only extended to include the player’s most-preferred outcome, not their PMP (call this a “self-favoring extension”). And even if a player uses a self-favoring extension as their final choice of program (the “outer loop”), they are still incentivized to use the PMP-extension within their default program (“inner loop”).
Second, while it is true that an analogous argument to the above could show that a player is weakly better off (in expected utility) using a self-favoring extension than not extending their renegotiation set at all, this does not undermine our argument. This is because it is reasonable to assume that among programs with equal expected utility, players prefer a program with a larger renegotiation set all else equal — i.e., prefer to include their PMP. On the other hand, due to the argument in the second bullet point above, players will not always want to include outcomes that Pareto-dominate the PMM as well.
Summary: Assumptions and result
Below, we summarize the assumptions we made, and the PMM bound we’re able to prove under those.
Assumptions
Type of game. As a base game, we can use any game of complete information. We can assume without loss of generality that players use renegotiation programs, under the mild assumption spelled out above. We do require, however, that players have the ability to make credible conditional commitments, as those are necessary to construct renegotiation programs.
Beliefs. As discussed above, each player has an incentive to PMP-extend their renegotiation set only if they believe that, in response, their counterpart’s renegotiation function will return a set that’s at least as favorable to them as the set that the function would’ve otherwise returned. This is a natural assumption, since if the counterpart chose a set that made the focal player worse off, the counterpart themselves would also be worse off. (I.e., this assumption is only violated if the counterpart pointlessly “punishes” the focal player.)
Selection function. Recall that if the agreement set (intersection of both player’s renegotiation sets) contains several outcomes, a selection function is used to select one of them. For our PMM bound result, we require that the selection function select a Pareto-efficient point among points in the agreement set, and satisfy the following transitivity property: If outcomes are added to the agreement set that make all players weakly better off than by default, the selected renegotiation outcome should be weakly better for all players.[24]
To see why we require this, consider the case depicted on the right panel of Fig. 6. Recall that the outcome selected by default by the selection function is represented by the empty circle. Now, suppose both players add their PMP of this point to their renegotiation set. A transitive selection function would then necessarily select the point at the intersection of the two PMPs (point shown by the arrow). On the other hand, a generic selection function could select another Pareto-optimal point in the agreement set, and in particular the one most favorable to Alice. But if that were the case, Bob would be worse off, and would thus have an incentive not to PMP-extend his set.
Result
Under the assumptions above, both players have no incentives not to PMP-extend their renegotiation sets. Thus, if both players choose the PMP-extension of some program over that program whenever they are indifferent between the two options, they are guaranteed their PMM or Pareto-better. See the appendix for a more formal proof of the result.
Future work
A key question is how prosaic AI systems can be designed to satisfy the conditions under which the PMM is guaranteed (e.g., via implementing surrogate goals), and what decision-theoretic properties lead agents to consider renegotiation strategies.
Other open questions concern conceptual aspects of SPIs:
- What are necessary and sufficient conditions on players’ beliefs for SPIs to guarantee efficiency?
- The present post provides a partial answer, as we’ve shown that mild assumptions on each player’s beliefs are sufficient for an upper bound on inefficiencies.
- When are SPIs used when the assumption of independent commitments is relaxed? I.e., either because a) agents follow non-causal decision theories and believe their choices of commitments are correlated with each other, or because b) the interaction is a sequential rather than simultaneous-move game.
- In unpublished work on case (b), we argue that under stronger assumptions on players’ beliefs, players are individually incentivized to use renegotiation programs with the following property: “Use the default program that you would have used had the other players not been willing to renegotiate. [We call this property participation independence.] Renegotiate with counterparts whose default programs satisfy participation independence.”
- AIs may not be expected utility maximizers. Thus, what can be said about individual SPI adoption, when the expected utility maximization assumption is relaxed?
Acknowledgements
Thanks to Akash Wasil, Alex Kastner, Caspar Oesterheld, Guillaume Corlouër, James Faville, Maxime Riché, Nathaniel Sauerberg, Sylvester Kollin, Tristan Cook, and Euan McLean for comments and suggestions.
Appendix A: Formal statement
In this appendix, we more formally prove the claim made in the main text. For more details, we refer the reader to DCM.
The result we’re interested in proving roughly goes as follows: “For any program a player might consider playing, this player is weakly better off playing instead the PMP-extension of such a program.” Note that in this appendix, we consider the generic case of players, while the text focuses on the two-player case for simplicity.
PMP-extension of a program
Let be the PMM of a given set of payoff profiles. The PMP for player of an outcome is formally defined as the set:
The PMP-extension of a program is the renegotiation program such that:
- Its default coincides with ’s default: ;
- Its renegotiation function maps each input (i.e., profile of counterpart renegotiation functions and default outcome) to all the same payoffs as , plus the PMP of the renegotiation outcome achieved by on that input. Formally, letting (resp. ) be the default (resp. renegotiation) outcome associated to , one has .
For any and any response function profile , let be the profile identical to , except that is replaced by .
Non-punishment condition
We say that believes that PMP-extensions won’t be punished if, for any counterpart programs that considers possible, these programs respond at least as favorably to the PMP-extension of any program might play than to the non-PMP-extended program.
More precisely, our non-punishment condition is as follows: For any counterpart profile that believes has a non-zero chance of being played, for any , , with .
The non-punishment assumption seems reasonable, since no player is better off responding in a way that makes worse off.
See also footnote 21 for another non-punishment assumption we make, which guarantees that players without loss of generality use renegotiation programs.
Formal statement of the claim
Main claim: Fix a base game and a program game defined over the base game, such that players have access to renegotiation programs. Assume they use a transitive selection function. Fix a player and assume that believes PMP-extensions are not punished. Then, for any program , player is weakly better off playing the PMP-extension .
Corollary (PMM bound): Assume that the conditions of the main result are fulfilled for all players, and assume moreover that whenever a player is indifferent between a program and its PMP-extension, they play the PMP-extension. Then, each player receives their PMM or more with certainty., in expectation.
Proof:
Let:
- be a counterpart program profile that believes might be played with non-zero probability;
- and be the default and renegotiation outcomes associated with , respectively;
- be the PMP-extension of ; and
- and be the agreement sets associated to and , respectively. That is, let and , where is by definition equal to if , and equal to otherwise.
If all players obtain at least their PMM under , then by the non-punishment assumption .
Otherwise, again by the non-punishment assumption, . Then:
- If , then and ;
- Otherwise:
- If , then and by definition of the PMP;
- Otherwise, by transitivity of the selection function we have , and thus .
Appendix B: Coordinating on a choice of selection function
In the main text, we assumed that players always coordinate on a choice of selection function. This appendix justifies this assumption. See also Appendix C of DCM.
Suppose that it’s common knowledge that a particular selection function, , will be used. Now, suppose one player says “I want to switch to .” For any given outcome, there is a renegotiation function profile that realizes that outcome under and a (generally different) renegotiation function profile that realizes that outcome under .[25] Thus, players can always “translate” whichever bargaining strategy they consider under to an equivalent bargaining strategy under . As a concrete example, suppose (resp. ) always selects an outcome that favors Alice (resp. Bob) the most. Bob will do poorer with than with , for any agreement set whose Pareto frontier is not a singleton. However, given , players can always transform their -renegotiation functions into renegotiation functions whose agreement set’s Pareto frontier is the singleton corresponding to what would have been obtained if had been used.
It therefore seems plausible that players expect their counterparts to bargain equivalently (no more or less aggressively), regardless of which selection function will be used. Thus, players have no particular reason to prefer one selection function to another, and will plausibly manage to coordinate on one of them. The intuition is that any bargaining problem over selection functions can be translated into the bargaining problem over renegotiation functions (which the PMP-extension resolves).
More formally: Suppose that it’s common knowledge that the selection function will be used. For any player , any selection function and any outcome , let be the set of counterpart renegotiation functions that achieve under (given that plays a renegotiation function that makes achieving possible).[26] Let be ’s belief that the counterparts will use renegotiation functions such that outcome obtains, given that will be used and given that plays a renegotiation function compatible with .
It seems reasonable that, for selection functions with , and for any outcome , we have . (Informally, player doesn’t expect the choice of selection function to affect how aggressively counterparts bargain. This is because if the selection function is unfavorable to some counterpart, such that they will always do poorly under some class of agreement sets, that counterpart can just pick a renegotiation set function that prevents the agreement set from being in that class.) Then, player expects to do just as well whether or is used. If this is true for any player and any pair of selection functions, players don’t have incentives not to coordinate on a choice of selection function.
- ^
An outcome is a Pareto improvement another outcome if all players weakly prefer to , and at least one player strictly prefers over . We’ll also sometimes say that Pareto dominates or that is Pareto-better than . An outcome is Pareto-efficient if it’s not possible to Pareto improve on it. The set of Pareto-efficient outcomes is called the Pareto frontier. We’ll say that weakly Pareto improves on if all players weakly prefer to .
- ^
“With certainty”: For any unmodified strategy each player might play.
- ^
For instance, in the example above, A might only agree to a lottery that allocates the territory to A with the probability that A wins the war, while B only agrees to a different lottery, e.g. one that allocates the territory with 50% probability to either player.
- ^
I.e., we don’t assume the agents engage in “cooperative bargaining” in the technical sense defined here.
- ^
I.e., by using commitments that conditionally disclose private information (see DiGiovanni & Clifton (2022)).
- ^
In particular, we require that each agent either (a) believes that which commitment they make gives negligible evidence about which commitments others may make, or (b) does not take such evidence into account when choosing what to commit to (e.g., because they are causal decision theorists).
- ^
Note that strategies themselves can condition on each other. For instance, in the Prisoner’s Dilemma, “Cooperate if {my counterpart’s code} == {my code}”. We discuss this in more detail in the section on “Program games.”
- ^
Namely: To show the result, we will construct a way for each player to unilaterally modify their bargaining strategy. Then, the assumption is that no player believes the others will bargain more aggressively if they themselves modify their strategy this way. This is a mild condition since no player is better off bargaining less aggressively conditional on the modification being made.
- ^
See also Diffractor’s (2022) cooperative bargaining solution that uses the PMM as the disagreement point. Diffractor (2022) doesn’t address the problem of coordinating on their bargaining solution.
- ^
Credits for the names of the players goes to Oesterheld & Conitzer (2022).
- ^
Because the game is symmetric, it might be tempting to believe that both players will always coordinate on the “natural” 50-50 split. However, as the next paragraph discusses, players might have beliefs such that they don’t coordinate on the 50-50 split. Furthermore, bargaining scenarios are generally not symmetric, and our goal here is to give the intuition for generic efficiency guarantees.
- ^
Note that we do not place any particular restriction on the set of bargaining strategies that can be used. In particular, players might have access to bargaining strategies that condition on each other.
- ^
While the above “maximally aggressive” commitments may be unlikely, it’s plausible that Aliceland would at least not want to always switch to a proposal that is compatible with Bobbesia’s, because then Bobbesia would be able to freely demand any share of the territory.
- ^
See Sec. 4.4 of DCM for more formal details.
- ^
In which case each action is a specification of how each player would play the next move from any one of their decision nodes in the game tree.
- ^
We’ll assume that the set of feasible profiles is convex, which is not a strong requirement, as it’s sufficient for players to have access to randomization devices to satisfy it. (This is standard in program game literature; see, e.g., Kalai et al. (2010).) If several action profiles realize the same payoff profile, we’ll arbitrarily fix a choice of action profile, so that we can (up to that choice) map outcomes and action profiles one-to-one. We will henceforth speak almost exclusively about outcomes, and not about the corresponding action profiles.
- ^
See Sec. 3.1 of DCM for more formal details.
- ^
This assumption is standard in the literature on program games / program equilibrium. See Oesterheld (2019) for a class of such programs. Also note that we are not interested in how programs work internally; for our purposes, the knowledge of the big lookup table that maps each program profile to the corresponding action profile will suffice. And indeed, these programs do not need to be computer programs per se; they could as well represent different choices of instructions that someone gives to a representative who bargains on their behalf (Oesterheld & Conitzer, 2022), or different ways in which an AI could self-modify into a successor agent that’ll act on their behalf in the future, etc. (See more discussion here.)
- ^
Oesterheld & Conitzer (2022) similarly consider SPIs of the form, “We’ll play the game as usual, but whenever we would have made incompatible demands, we’ll instead randomize over Pareto-efficient outcomes”; see Sec. 5, “Safe Pareto improvements under improved coordination.” The difference between this and our approach is that we do not exogenously specify an SPI, but instead consider when players have individual incentives to use programs that, as we’ll argue, implement this kind of SPI and achieve the PMM guarantee.
- ^
See Sec. 4.1 and 4.2 of DCM for more formal details.
- ^
In more detail (see Assumption 8(i) of DCM), the assumption is as follows: For any non-renegotiation program that is subjectively optimal (from ’s perspective) and for any counterpart renegotiation program with default , we have . Further, for any counterpart program that thinks might play with non-zero probability, and for any renegotiation program with default , .
- ^
Formally, .
- ^
Note that, for our result that players are guaranteed at least their PMM payoffs, it’s actually sufficient for each player to just add the outcome in their PMP that is worst for themselves. We add the entire PMP because it’s plausible that, all else equal, players are willing to renegotiate to outcomes that are strictly better for themselves.
- ^
Formally: The selection function is transitive if, whenever the agreement set can be written , such that for any , , we have .
- ^
Indeed, the renegotiation profile such that all functions return the singleton guarantees outcome , for any selection function .
- ^
For any outcome , we can assume that there's a unique set of renegotiation functions that achieve against each other. Indeed, if several such sets exist, players can just coordinate on always picking their renegotiation functions from any given set.