Latent variables for prediction markets: motivation, technical guide, and design considerations
10SG
3tailcalled
1SG
3tailcalled
2tailcalled
6Donald Hobson
5tailcalled
2Donald Hobson
1kenakofer
3tailcalled
1kenakofer
3tailcalled
1kenakofer
2tailcalled
4niplav
4tailcalled
2tailcalled
1Abhimanyu Pallavi Sudhir
2tailcalled
1Abhimanyu Pallavi Sudhir
2tailcalled
1Aaro Salosensaari
2tailcalled
0Adam Shen
2tailcalled
New Comment
Thanks for writing such a thorough article! I’d be interested in seeing how LVPMs work in practice, but I must admit I’m coming from a position of extreme skepticism: Given how complicated real-world situations like the Russia/Ukraine war are, I’m skeptical a latent variable model can provide any marginal price efficiency over a simple set of conditional and unconditional markets.
My suspicion is that if a LVPM were created for a question like “Will China invade Taiwan by 2030?” that most of the predictive power would come from people betting directly on the latent variable rather than from any model-provided updates as a result of people betting on indicator variables. The number, type, and conditional dependency graph of indicator variables is too complicated to capture in a simple model and would function worse than human intuition, imho.
Other thoughts:
- For LVPM to be useful, you’d probably want to add/remove indicator variables in real-time. What would be the process for doing this be? What is the payout of someone who bet before certain indicator variables were added? (This is sort of similar to the problems Manifold has faced in determining payouts for free-response markets.)
- Price efficiency will suffer if you can’t sell your position before resolution or can’t provide liquidity in the form of a limit order or AMM liquidity provision. I think all of these problems are solvable in theory, but may require a good deal more mathematical cleverness.
- Making a compelling UI for a LVPM is a hard problem.
- I can't make any guarantees, but the first step to getting a prototype of this up and running on Manifold (or elsewhere) would be creating a typescript npm package with the market logic. You might be able to convince me to work on this at our next hackathon...
Thanks for the reply!
Given how complicated real-world situations like the Russia/Ukraine war are, I’m skeptical a latent variable model can provide any marginal price efficiency over a simple set of conditional and unconditional markets.
When you say "a simple set of conditional and unconditional markets", what do you have in mind?
Edit: I mean for a specific case such as the Russia/Ukraine war, what would be some conditional and unconditional markets that could be informative? (I understand how conditional and unconditional markets work in principle, I'm more interested in how it would practically compete with LVPMs.)
My suspicion is that if a LVPM were created for a question like “Will China invade Taiwan by 2030?” that most of the predictive power would come from people betting directly on the latent variable rather than from any model-provided updates as a result of people betting on indicator variables. The number, type, and conditional dependency graph of indicator variables is too complicated to capture in a simple model and would function worse than human intuition, imho.
So I am not 100% sure what you are referring to here. When you are talking about "model-provided updates as a result of people betting on indicator variables", I can think of two things you might be referring to:
- If someone bets directly on a market , i.e. changing to a new value, then (using some math) we can treat this as evidence to update , using the fact that we know .
- If someone bets on a conditional market , then the parameters of this conditional market may change, which in a sense constitutes an update as a result of people betting on indicator variables.
- (Possibly something else?)
Your language makes me think you are referring to 1, and I agree that this will plausibly be of limited value. I'm most excited about 2 because it allows people to better aggregate information about the plausible outcomes, while taking correlations into account.
- For LVPM to be useful, you’d probably want to add/remove indicator variables in real-time. What would be the process for doing this be? What is the payout of someone who bet before certain indicator variables were added? (This is sort of similar to the problems Manifold has faced in determining payouts for free-response markets.)
You can treat the addition or removal of an indicator as a trade performed by the market owner. The payout for a person for a trade does not depend on any trades that happen after the person's . (This follows from the fact that we describe the payoffs as a function of the probabilities just before and just after .) So the owner of the market can add and remove however many indicator variables they want without any trouble.
- Price efficiency will suffer if you can’t sell your position before resolution or can’t provide liquidity in the form of a limit order or AMM liquidity provision. I think all of these problems are solvable in theory, but may require a good deal more mathematical cleverness.
I think the part of my scoring counts as an AMM liquidity provision? I might be misunderstanding what AMM liquidity provision means.
To scale up the liquidity, one can multiply this expression by the expression by some constant so there is a deeper pool of liquidity.
Of course, a consequence of this is that the person creating the latent variable market has to provide enough liquidity to cover this, i.e. to create a market with a starting state , they would have to pay . In practice I would assume is like 1, so it reduces to , which for e.g. a predicting uniform distribution over would be where is the number of indicators.
- Making a compelling UI for a LVPM is a hard problem.
At first glance this seems true; my UI seems to have confused people. However, I am not a designer.
I should probably repeat my request for a designer to work with.
- I can't make any guarantees, but the first step to getting a prototype of this up and running on Manifold (or elsewhere) would be creating a typescript npm package with the market logic. You might be able to convince me to work on this at our next hackathon...
Hm, this sounds like a task that would be relatively isolated from the rest of your codebase, and therefore something I could do independently without learning much of Manifold Market's code? I would be up for programming this. Do you have any examples of similar modules in your codebase right now that I can look at, to see what interface it should provide?
When you say "a simple set of conditional and unconditional markets", what do you have in mind?
Unconditional: "Will China invade Taiwan by 2030?"; Conditional: "If China experiences a recession any time before 2030, will China invade Taiwan by 2030?"
Your language makes me think you are referring to 1, and I agree that this will plausibly be of limited value.
Isn't estimating from most of the value of LVPMs?!
I think the part of my scoring counts as an AMM liquidity provision?
Yes, that's correct; if the market creator is willing to issue these payouts, then they are playing the role of AMM.
The question is how to add third-party liquidity provision to this system, i.e. where users can inject and remove liquidity from the market to increase payouts for traders (ideally while being compensated for their efforts).
Hm, this sounds like a task that would be relatively isolated from the rest of your codebase, and therefore something I could do independently without learning much of Manifold Market's code?
That's the idea. You can see some example code for our Uniswap-style AMM here, but honestly, any well-designed api would be fine. What I'd like is: 1. A typescript interface that defines the current state of a LVPM at any given point, 2. Betting function: Given a bet on some variable and the current market state, return the new market state and user position, 3. Resolution function: given the current market state, the final outcome of the market, and a list of user positions, return a list of all the user payouts.
Unconditional: "Will China invade Taiwan by 2030?"; Conditional: "If China experiences a recession any time before 2030, will China invade Taiwan by 2030?"
...
Isn't estimating from most of the value of LVPMs?!
Kind of. The point is to estimate . However, the value is not supposed to come from automatically estimating , but rather from providing an objective way of scoring manual predictions about P(Y) when we don't have an objective definition of .
I agree that if the goal was to automatically predict from , structures of conditional prediction markets seems better. See also the "Latent variable markets vs combinatorial markets" section of my post; there are some cases where e.g. is more interesting.
So basically, yes, the value of LVPMs comes from estimating , but the way we estimate is by having people make predictions on . All the elaborate has the primary purpose of providing a way to objectively score predictions on , and a secondary purpose of providing information/common knowledge about the domain of applicability of the concept.
Yes, that's correct; if the market creator is willing to issue these payouts, then they are playing the role of AMM.
One thing I guess I should note is that the market maker only has to pay the first person. To clarify how this works, suppose the market maker creates a market with initial state , and a first trader then updates this state to , and a second trader then updates the state to . Assuming for simplicity that the initial distribution is uniform over , when the market resolves to a specific , we can then read the payoffs here:
- The second trader gets a payout of .
- The first traders gets a payout of .
- The market maker paid for making the market, which we can think of them as getting a payout of to make the signs of the expressions all aligned.
If we add all of these payouts up, we get , which in general is a nonpositive number[1], and so the market will never give a greater payout than what is put in. Essentially what happens is that each trader pays off the next trader, guaranteeing that it all adds up. (This won't require the individual traders to pay any huge amount of money, because they are always paying relative to , which accounts for most of the pool.)
The question is how to add third-party liquidity provision to this system, i.e. where users can inject and remove liquidity from the market to increase payouts for traders (ideally while being compensated for their efforts).
I think if people add some additional liquidity, one can just find a new scale factor on the payoffs that continues to make everything add up?
That's the idea. You can see some example code for our Uniswap-style AMM here, but honestly, any well-designed api would be fine. What I'd like is: 1. A typescript interface that defines the current state of a LVPM at any given point, 2. Betting function: Given a bet on some variable and the current market state, return the new market state and user position, 3. Resolution function: given the current market state, the final outcome of the market, and a list of user positions, return a list of all the user payouts.
Thanks! I'll take a look.
I'm thinking I should maybe implement LVPMs based on latent class analysis rather than item response theory because it is easier to design an interface for and get an intuition for (since LCA literally just enumerates the set of possible outcomes).
- ^
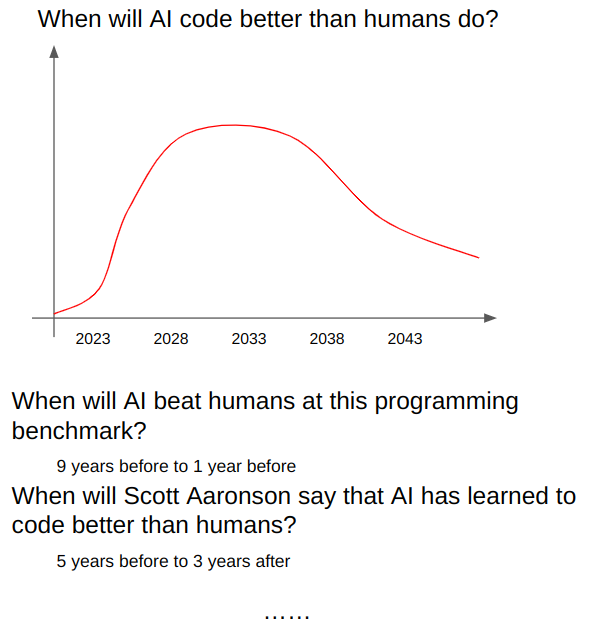
though presumably often rather than just , because as the close date nears, \vec x is going to be better and better known, and so the probaility is going to move towards 1
I can't see anything that pins down the latent variable other than Schelling point inertia. Or do interpretations that support correlation intrinsically get favored?
If I understand your question correctly, then yes, interpretations that support correlation intrinsically get favored.
Strictly speaking, there is a sense in which we can entirely ignore when understanding what the latent variable markets are doing. A latent variable market over a set of variables is really trying to predict their join distribution . If these variables are all "getting at the same thing" from different angles, then they will likely "fall within a subspace", and it is this subspace that the LVPMs are characterizing.
For instance consider the following plot of a probability distribution:
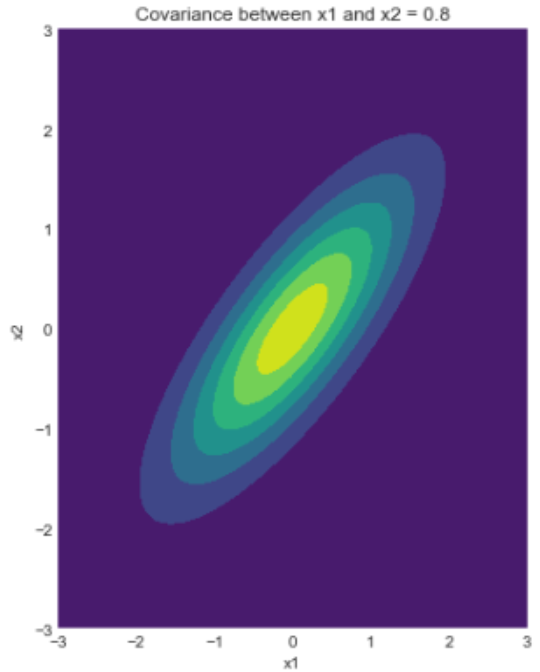
There is a ridge where x1 and x2 are similar in magnitude, and most of the probability mass is distributed along that ridge. It is unlikely for x1 to be 1 while x2 is -1, or vice versa.
The LVPMs characterize this ridge of high probability, so an LVPM on a probability distribution like the above would likely range from "x1 and x2 are both low" to "x1 and x2 are both high".
If you are familiar with principal component analysis, it may be helpful to think of LVPMs as doing a similar thing.
So if I'm understanding correctly, you're saying a LVPM market Y could be displayed without a title, and traders would still converge toward finding the joint probability distribution function? So instead of making a LVPM titled "Will Ukraine do well in defense against Russia?", I could make a LVPM that says "Hey, here are a bunch of existing objective questions that may or may not be correlated, have at it", and it would be just as functional?
If so that's pretty neat. But what stops Trader1 from interpreting Y as "Will Ukraine do well in defense against Russia?" while Trader2 treats it as "Will Russia do well in the invasion of Ukraine?" IIUC, these two traders would make nearly opposite trades on the conditional probabilities between each X and Y.
So if I'm understanding correctly, you're saying a LVPM market Y could be displayed without a title, and traders would still converge toward finding the joint probability distribution function? So instead of making a LVPM titled "Will Ukraine do well in defense against Russia?", I could make a LVPM that says "Hey, here are a bunch of existing objective questions that may or may not be correlated, have at it", and it would be just as functional?
Yep.
If so that's pretty neat. But what stops Trader1 from interpreting Y as "Will Ukraine do well in defense against Russia?" while Trader2 treats it as "Will Russia do well in the invasion of Ukraine?" IIUC, these two traders would make nearly opposite trades on the conditional probabilities between each Xi and Y.
So this is in fact true: LVPMs will not be totally unique, but instead have symmetries where some options do equally well. The exact type of symmetry depends on the kind of market, but they mainly look like what you describe here: swapping around the results such that yes becomes no and no becomes yes.
The way I usually handle that problem is by picking one of the indicators as a "reference indicator" and fixing it to have a specific direction of relationship with the outcome. If the reference indicator cannot be flipped, then all the other indicators have to have a fixed direction too. (One could also do something more nuanced, e.g. pick many reference indicators.)
I don't know whether this is necessary for humans. I mainly do this with computers because computers have no inherent idea which direction of the LV is most natural for humans.
I don't know if it would be a problem for people. It's not something that happens iteratively; while you can flip all the parameters at once and still get a good score, you cannot continuously change from one optimum to an opposite optimum without having a worse score in the middle. So if it is an issue, it will probably mainly be an issue with trolls.
So this is in fact true: LVPMs will not be totally unique, but instead have symmetries where some options do equally well. The exact type of symmetry depends on the kind of market, but they mainly look like what you describe here: swapping around the results such that yes becomes no and no becomes yes.
I'm not a savvy trader by any means, but this sets off warning bells for me that more savvy traders will find clever exploits in LVPMs. You can't force anyone to abide by the spirit of the market's question, they will seek the profit incentive wherever it lies.
(I feel somewhat satisfied that the "question reversal" symmetry is ruled out by the market maker restricting the possible PDF space (in half along one specified dimension, IIUC). I'm curious how that would be practically implemented in payouts.)
I worry about these other possible symmetries or rotations, which I can't yet wrap my head around. I would love an illustrating example showing how they work and why we should or shouldn't worry about them.
I'm not a savvy trader by any means, but this sets off warning bells for me that more savvy traders will find clever exploits in LVPMs. You can't force anyone to abide by the spirit of the market's question, they will seek the profit incentive wherever it lies.
Hmm I'm not sure what exploits you have in mind. Do you mean something like, they flip the meaning of the market around, and then people who later look at the market get confused and bet in the opposite direction of what they intended? And then the flipper can make money by undoing their bets?
Or do you mean something else?
I feel somewhat satisfied that the "question reversal" symmetry is ruled out by the market maker restricting the possible PDF space (in half along one specified dimension, IIUC).
Yep, in half along one specified dimension.
I'm curious how that would be practically implemented in payouts.
There's a few different ways.
If someone bets to set the market state to a that flips the fixed dimension, the market implementation could just automatically replace their bet with so it doesn't flip the dimension. The payouts are symmetric under flips, so they will get paid the same regardless of whether they bet or .
Alternatively you could just forbid predictions in the UI that flip the fixed dimension.
I worry about these other possible symmetries or rotations, which I can't yet wrap my head around. I would love an illustrating example showing how they work and why we should or shouldn't worry about them.
Flipping is the only symmetry that exists for unidimensional cases.
If you have multiple dimensions, you have a whole continuum of symmetries, because you can continuously rotate the dimensions into each other.
Thanks for being patient with my questions. I'm definitely not solid enough on these concepts yet to point out an exploit or misalignment. It would be super helpful if you fill out your LVPM playground page in the near future with a functional AMM to let people probe at the system.
Flipping is the only symmetry that exists for unidimensional cases.
If you have multiple dimensions, you have a whole continuum of symmetries, because you can continuously rotate the dimensions into each other.
What do you mean by unidimensional cases? So like if the binary LVPM is made up of binary markets to , I would have called that an N-dimensional case, since the PDF is N-dimensional. How many symmetries and "possible convergences" does this have?
Thanks for being patient with my questions.
No problem, answering questions is the point of this post. 😅
It would be super helpful if you fill out your LVPM playground page in the near future with a functional AMM to let people probe at the system.
The playground page already has this. If you scroll down to the bottom of the page, you will see this info:
To play with the payout and get an intuition for it, you can use the checkboxes below. Your bets have currently cost proportional to 0 Mana, and if the outcome below happens, you get a payout proportional to 0 Mana, for a total profit proportional to 0 Mana.
- Japan hyperinflation by 2030?
- US hyperinflation by 2030?
- Ukraine hyperinflation by 2030?
If you make bets, then the numbers in this section get updated with the costs and the payouts.
But I guess my interface probably isn't very friendly overall, even if it is there. 😅
What do you mean by unidimensional cases? So like if the binary LVPM is made up of binary markets to , I would have called that an N-dimensional case, since the PDF is N-dimensional. How many symmetries and "possible convergences" does this have?
I am talking about the dimensionality of , not the dimensionality of .
In the markets I described in the post and implemented for my demo, is always one-dimensional. However, it is possible to make more advance implementations where can be multidimensional. For instance in the uncertainty about the outcome of the Ukraine war, there is probably not just a Ukraine wins <-> Russia wins axis, but also a war ends <-> war continues axis.
I really liked this post when I read it, even though I didn't quite understand it to my satisfaction (and still don't).
As far as I understand the post, it proposes a concrete & sometimes fleshed-out solution for the perennial problem of asking forecasting questions: How do I ask a forecasting question that actually resolves the way I want it to, in retrospective, and doesn't just fall on technicalities?
The proposed solution is latent variables and creating prediction markets on them: The change in the world (e.g. AI learning to code) is going to affect a bunch of different variables, so we set up a prediction market for each of those, and then (through some mildly complicated math) back out the actual change in the latent variable, not just the technicalities on each of the markets.
This is pretty damn great: It'd allow us to more quickly communicate changes in predictions about the world to people and read prediction market changes more easily. The downside is that betting on such markets would be more complicated and effortful, and especially for non-subsidized markets that is often a breaking point. (Many "boring" Metaculus questions receive <a few dozen predictions.)
I'm pretty impressed by this work, and wish there was some efforts at integration into existing platforms. Props to tailcalled for writing code and an explanation for this post. I'll give it +4, maybe even +9, because it represents genuine progress on a tricky intellectual question.
Prediction markets are good at eliciting information that correlates with what will be revealed in the future, but they treat each piece of information independently. Latent variables are a well-established method of handling low-rank connections between information, and I think this post does a good job of explaining why we might want to use that, as well as how we might want to implement them in prediction markets.
Of course the post is probably not entirely perfect. Already shortly after I wrote it, I switched from leaning towards IRT to leaning towards LCA, as you can see in the comments. I think it's best to think of the post as staking out a general shape for the idea, and then as one goes to implementing it, one can adjust the details based on what seems to work the best.
Overall though, I'm now somewhat less excited about LVPMs than I was at the time of writing it, but this is mainly because I now disagree with Bayesianism and doubt the value of eliciting information per se. I suspect that the discourse mechanism we need is not something for predicting the future, but rather for attributing outcomes to root causes. See Linear Diffusion of Sparse Lognormals for a partial attempt at explaining this.
Insofar as rationalists are going to keep going with the Bayesian spiral, I think LVPMs are the major next step. Even if it's not going to be the revolutionary method I assumed it would be, I would still be quite interested to see what happens if this ever gets implemented.
I don't know of a neat way to achieve this with latent variable markets. So I guess it won't be supported?
Actually, I suppose one could use gradient descent to figure out a trade that gives the largest guaranteed profit, and then implement that trade? That would be sort of like selling one's shares. I don't know how well that would work in practice though. I suspect it would work OK?
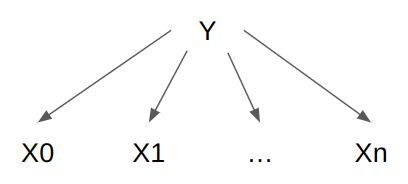
Bayesian networks support latent variables, and so allowing general Bayesian networks can be considered a strict generalization of allowing latent variables, as long as one remembers to support latent variable in the Bayesian network implementation.
Correct me if I'm wrong, but I believe this isn't necessarily true.
The most general Bayesian network prediction market implementation I'm aware of is the SciCast team's graphical model market-maker. Say a trader bets up a latent variable -- and this correctly increases the probability of its child variables (which all resolve True).
Under your model you would (correctly, IMO) reward the trader for this, because you are scoring it for the impact it has on the resolved variables. But under their model, another trader can come and completely flip , while also adjusting each conditional probability -- without affecting the overall score of the model, but screwing over the first trader completely because the first trader just owns some stocks which are now worth much less.
Your linked paper is kind of long - is there a single part of it that summarizes the scoring so I don't have to read all of it?
Either way, yes, it does seem plausible that one could create a market structure that supports latent variables without rewarding people in the way I described it.
Epistemic status: I am probably misunderstanding some critical parts of the theory, and I am quite ignorant on technical implementation of prediction markets. But posting this could be useful for my and others' learning.
First question. Am I understanding correctly how the market would function. Taking your IRT probit market example, here is what I gather:
(1) I want to make a bet on the conditional market P(X_i | Y). I have a visual UI where I slide bars to make a bet on parameters a and b; (dropping subscript i) however, internally this is represented by a bet on a' = a sigma_y and P(X) = Phi(b'/sqrt(a'+1)), b' = b + a mu_y. So far, so clear.
(2) I want to bet on the latent market P(Y). I make bet on mu_Y and sigma_y, which is internally represented by a bet on a' and P(X). In your demo, this is explicit: P(Y) actually remains a standard normal distribution, it is the conditional distributions that shift.
(3) I want to bet on the unconditional market P(X_i), which happens to be an indicator variable for some latent variable market I don't really care about. I want to make a bet on P(X_i) only. What does exactly happen? If the internal technical representation is a database row [p_i, a'] changing to [p_new, a'], then I must be implicitly making a bet on a' and b' too, as b' derived from a and P(X) and P(X) changed. In other words, it appears I am also making a bet on the conditional market?
Maybe this is OK if I simply ignore the latent variable market, but I could also disagree with it: I think P(X) is not correlated with the other indicators, or the correlation structure implied by linear probit IRT model is inadequate. Can I make a bet of form [p_i, NA] and have it not to participate in the latent variable market structure? (Ie when the indicator market resolves, p_i is taken into account for scoring, NA is ignored while scoring Y).
Thus, I can launch a competing latent variable market for the same indicators? How can I make a bet against a particular latent structure in favor of another structure? A model selection bet, if you will.
Context for the question: In my limited experience of latent variable models for statistical inference tasks, the most difficult and often contested question is whether the latent structure you specified is good one. The choice of model and interpretations of it are very likely to get criticized and debated in published work.
Another question for discussion.
It seems theoretically possible to obtain individual predictors' bets / predictions on X_1 ... X_k, without presence of any latent variable market, impute for the missing values if some predictors have not predicted on all k indicators, and then estimate a latent variable model on this data. What is the exact benefit of having the latent model available for betting? If fit a Bayesian model (non-market LVM with indicator datapoints) and it converges, from this non-market model, I would obtain posterior distribution for parameters and compute many of the statistics of interest.
Presumably, if there is a latent "ground truth" relationship between all indicator questions and the market participants are considering them, the relationship would be recovered by such analysis. If the model is non-identifiable or misspecified (= such ground truth does not exist / is not recoverable), I will have problems fitting it and with the interpretation of fit. (And if I were to run a prediction market for a badly specified LVM, the market would exhibit problematic behavior.)
By not making a prediction market for the latent model available, I won't have predictions on the latent distribution directly, but on the other hand, I could try to estimate several different without imposing any of their assumptions about presumed joint structure on the market. I could see this beneficial, depending on how the predictions on Y "propagate" to indicator markets or the other way around (case (3) above).
Final question for discussion: Suppose I run a prediction market using the current market implementations (Metaculus or Manifold or something else, without any LVM support), where I promise to fit a particular IRT probit model at time point t in future and ask for predictions on the distribution of posterior model parameters estimates when I fit the model. Wouldn't I obtain most of the benefits of "native technical implementation" of a LVM market ... except that updating away any inconsistencies between the LVM prediction market estimate and individual indicator market will be up to to individual market participants? The bets on this estimated LVM market at least should behave as any other bets, right? (Related: which should be the time point t when I promise to fit the model and resolve the market? t = when the first indicator market resolves? when the last indicator market resolves? arbitrary fixed time point T?)
(1) I want to make a bet on the conditional market P(X_i | Y). I have a visual UI where I slide bars to make a bet on parameters a and b; (dropping subscript i) however, internally this is represented by a bet on a' = a sigma_y and P(X) = Phi(b'/sqrt(a'+1)), b' = b + a mu_y. So far, so clear.
Yep.
(Or maybe not a and b, but some other parameterization; I would guess the most intuitive UI is still an open question.)
(2) I want to bet on the latent market P(Y). I make bet on mu_Y and sigma_y, which is internally represented by a bet on a' and P(X). In your demo, this is explicit: P(Y) actually remains a standard normal distribution, it is the conditional distributions that shift.
Yep.
(3) I want to bet on the unconditional market P(X_i), which happens to be an indicator variable for some latent variable market I don't really care about. I want to make a bet on P(X_i) only. What does exactly happen? If the internal technical representation is a database row [p_i, a'] changing to [p_new, a'], then I must be implicitly making a bet on a' and b' too, as b' derived from a and P(X) and P(X) changed. In other words, it appears I am also making a bet on the conditional market?
Maybe this is OK if I simply ignore the latent variable market, but I could also disagree with it: I think P(X) is not correlated with the other indicators, or the correlation structure implied by linear probit IRT model is inadequate. Can I make a bet of form [p_i, NA] and have it not to participate in the latent variable market structure? (Ie when the indicator market resolves, p_i is taken into account for scoring, NA is ignored while scoring Y).
Thus, I can launch a competing latent variable market for the same indicators? How can I make a bet against a particular latent structure in favor of another structure? A model selection bet, if you will.
Context for the question: In my limited experience of latent variable models for statistical inference tasks, the most difficult and often contested question is whether the latent structure you specified is good one. The choice of model and interpretations of it are very likely to get criticized and debated in published work.
Good question! This is actually a problem that I didn't realize at the time I started promoting LVPMs, though I did realize it somewhere along the way, albeit underestimating it and expecting it to solve itself, though somewhere along the way I realized that I had underestimated it. I still think it is only a very minor problem, but lemme give my analysis:
There are multiple ways to implement this type of bet, and your approach of changing [p_old, a'] to [p_new, a'] is only one of them; it was the one I favored earlier on, but there's an alternate approach that others have favored, and in fact there's a first approach that I've now come to favor. Let's take all of them.
The approach described by my post/by you: Assuming that we change the internal representation in the database from [p_old, a'] to [p_new, a'], this is equivalent to making a bet on the latent variable market that only affects b. So essentially you would be making a bet that b has higher probability across the entire latent variable.
As part of my initial push, I made the mistake of assuming that this was equivalent to just making a bet on X without the latent variable market, but then later I realized I was mixing up negative log probs and logits (you are making a bet that b has higher logit across the latent variable, but a prediction market without latent variables would be making a bet that b has higher negative log probabilities, not higher logits).
Conventional approach: I think the approach advocated by e.g. Robin Hanson is to have one grand Bayes net structure for all of the markets that anyone can make predictions on, and then when people make a prediction on only a subset of the structure, such as an indicator variable, then that bet is treated as virtual evidence which is used to update the entire Bayesian network.
This is basically similar in consequences to what you describe: if people make a bet on some indicator variable, they make implied bets on lots of other things too. However the implied bets are more complicated and less risky to the better than the version described in my post. (When I had written the post, I hadn't realized those complexities.)
In order to make a model selection bet, you would bet directly on the Bayes net structure that hangs around all of the markets, rather than betting on X directly.
I think the conventional approach has traditionally mainly struggled because it's had to deal with making Bayesian updates on a huge Bayes net. I would prefer something more atomic/discrete, and I would not be surprised if Manifold Markets would prefer something more atomic/discrete too. Treating it as Bayesian updates is also a bit of a problem for certain latent variable models, since e.g. if you fix the distribution of your latent variable to be Gaussian, then there are certain Bayesian updates that you cannot exactly do.
My new preferred approach: Rather than thinking of the LVPM as sharing parameters with the indicator markets (i.e. the model), I'd probably be inclined to give it separate parameters (i.e. a model). Of course then the trouble is that we could enter into an inconsistent state where the probabilities implied by the LVPM do not equal the probabilities from the indicator markets.
Ideally to minimize confusion and maximize information flow, we would like to go from an inconsistent state to a consistent state as quickly as possible. I think this could be done with an arbitrage bot (it seems like most of the time this would probably be +EV, so the bots should remain solvent), though perhaps the market should offer users to automatically make the arbitrage bets themselves so they can benefit from the presence of the latent variables.
I expect to give an update on this later with more formal derivations, likely together with my implementation of latent class markets for Manifold.
It seems theoretically possible to obtain individual predictors' bets / predictions on X_1 ... X_k, without presence of any latent variable market, impute for the missing values if some predictors have not predicted on all k indicators, and then estimate a latent variable model on this data. What is the exact benefit of having the latent model available for betting? If fit a Bayesian model (non-market LVM with indicator datapoints) and it converges, from this non-market model, I would obtain posterior distribution for parameters and compute many of the statistics of interest.
Presumably, if there is a latent "ground truth" relationship between all indicator questions and the market participants are considering them, the relationship would be recovered by such analysis. If the model is non-identifiable or misspecified (= such ground truth does not exist / is not recoverable), I will have problems fitting it and with the interpretation of fit. (And if I were to run a prediction market for a badly specified LVM, the market would exhibit problematic behavior.)
By not making a prediction market for the latent model available, I won't have predictions on the latent distribution directly, but on the other hand, I could try to estimate several different without imposing any of their assumptions about presumed joint structure on the market. I could see this beneficial, depending on how the predictions on Y "propagate" to indicator markets or the other way around (case (3) above).
Strictly speaking, it's an empirical question how well this would work.
I could certainly imagine programmatically fitting a latent variable model to prediction market data, assuming that there is a fixed set of outcomes and the users mainly disagree about the latent variable values. However, it seems to me that this would run into massive problems due to e.g. Kelly betting where people don't update the probabilities all the way to match their beliefs. You could probably attempt to model the participant's risk aversion etc., but I have a hard time believing that it would work.
Final question for discussion: Suppose I run a prediction market using the current market implementations (Metaculus or Manifold or something else, without any LVM support), where I promise to fit a particular IRT probit model at time point t in future and ask for predictions on the distribution of posterior model parameters estimates when I fit the model. Wouldn't I obtain most of the benefits of "native technical implementation" of a LVM market ... except that updating away any inconsistencies between the LVM prediction market estimate and individual indicator market will be up to to individual market participants? The bets on this estimated LVM market at least should behave as any other bets, right?
Asking for predictions about the parameters of the model would make it more like a method of moments estimator than a maximum likelihood estimator, right? Or maybe not, it seems kind of hard to predict how exactly it would go.
Regardless, I don't think this is an unreasonable idea to experiment with, but I think there are two challenges:
- As mentioned, I'm pretty skeptical of the notion that you can fit LV models to prediction market predictions and have it work well.
- If you don't have LVPM support, the UI for making predictions would probably be even worse than the UI I made.
I think if this was somehow changed to be maximum likelihood, and if those two challenges were removed, then you would get something close to "My new preferred approach".
P(→Xi)=∑jpj∏iXiqi,j+(1−Xi)(1−qi,j)
Maybe I'm missing something, but if we are estimating the P(Xi), how can we also have Xi on RHS? and what is the adjustment +(1−Xi)(1−qi,j). why is that there?
Maybe I'm missing something, but if we are estimating the P(Xi), how can we also have Xi on RHS?
These probabilities are used for scoring predictions over the observed variables once the market resolves, so at that point we "don't need" P(Xi) because we already know what Xi is. The only reason we compute it is so we can reward people who got the prediction right long ago before Xi was known.
and what is the adjustment +(1−Xi)(1−qi,j). why is that there?
Xiqi,j+(1−Xi)(1−qi,j) is equivalent to "qi,j if Xi = 1; otherwise 1-qi,j if Xi = 0". It's basically a way to mathematize the "contigency table" aspect.
Curated and popular this week