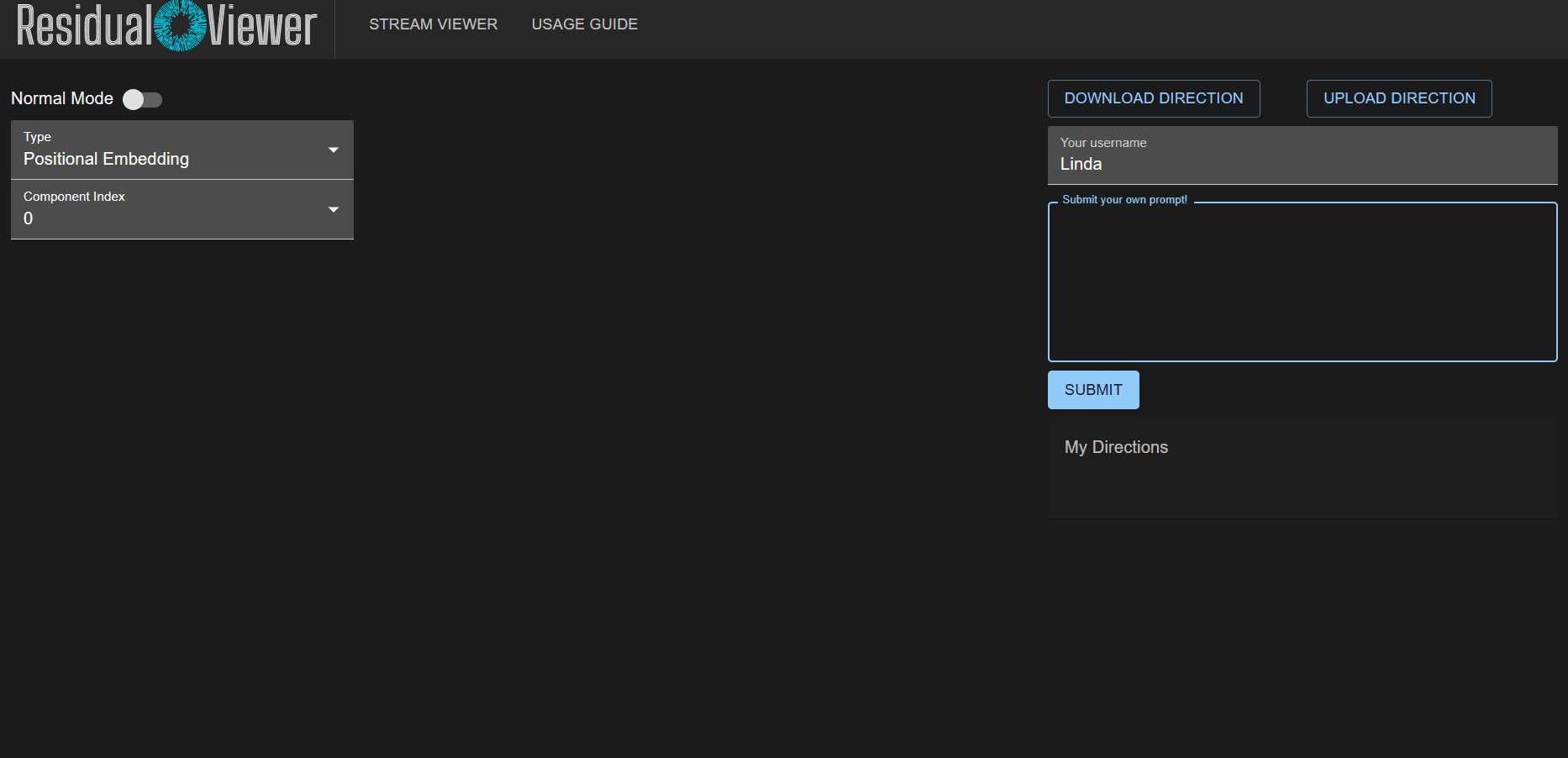
This is a link-post for the residual stream viewer, which can be found here. It's an online tool whose goal is to make it easier to do interpretability research by letting you easily look at directions within the residual stream. It's still in a quite early/unpolished state, so there may be bugs, and any feature requests are very welcome! I'll probably do more to flesh this out if I get the sense that people are finding it useful. 

Very briefly, the tool lets you see what the dot product of the residual stream at each token is with a particular direction. The default directions that you can look at using the tool were found by PCA, and I think many of them are fairly interpretable even at a glance (though it's worth noting that even if they correlate heavily with an apparent feature, that's no guarantee the network is actually using those directions).

Here's a screenshot of the current version of the tool:

There's a YouTube tutorial for the tool available here. I endorse the YouTube tutorial as probably a better way to get acquainted with the tool than the usage guide; but I'll copy-paste the usage guide for the remainder of the post.

The residual stream viewer is a tool for finding interesting directions in the residual stream of GPT2-small, for writing explanations for those directions and reading the explanations left by others, and for constructing new directions out of linear combinations of old ones.

A more detailed explanation of how transformers networks work and what the residual stream is can be found here. If you want to actually understand what the residual stream is and how transformers work, the text that follows here is hopelessly insufficient, and you should really follow the earlier link. However, as a very brief summary of what the "residual stream" is:

The residual stream can be thought of as the intermediate state of the transformer network's computation. It is the output of each layer of the network before it is fed into the next layer. Each prompt is split into "tokens," i.e. subparts of the prompt that roughly correspond to words or parts of words. At each layer, each token has its own associated residual stream vector. The residual stream at the beginning of the network, before any layer has acted, is equal to the "Token Embedding", i.e. the "meaning" of that token as encoded by a 768-dimensional vector, plus the "Positional embedding", i.e. the "meaning" of that token's position in the prompt as encoded by a 768-dimensional vector. Each layer acts on the residual stream by reading certain parts of the residual stream, doing some computation on them, and then adding the result back into the residual stream. At the end of the network, the residual stream is transformed into a probability distribution over which token comes next.

It's not easy to directly interpret a 768-dimensional vector, let alone one at each layer and at each token in the prompt. It's the purpose of this tool to make the job of interpreting such vectors easier. One way of interpreting the residual stream is by considering different possible directions in the residual stream. By analogy, imagine if there was a arrow in front of you, oriented somehow in space. The arrow represents the residual stream. One way you might approach describing the arrow's direction is by considering how "northerly" the arrow's direction is; that is, to what degree the arrow is pointing North. If the arrow was pointing northward, we might say that the arrow had positive northerliness, and if the arrow was pointing southward, we might say that the arrow had negative northerliness. An arrow pointing northeast could still be said to have positive northerliness; it wouldn't have to be pointing exactly north. If we wanted to classify arrows by their northerliness, and color them accordingly, we might color arrows pointing northwest or northeast or directly north blue, and color arrows pointing southwest or southeast or directly south red. Arrows that pointed in a direction orthogonal to the north-south direction could be left uncolored.

We can apply the same concept to directions in the residual stream. Unlike an arrow in three-dimensional space, which has three dimensions, the residual stream has 768 dimensions, but the same principle applies. When you choose a direction with the residual stream viewer, each of residual streams at each token will light up blue or red depending on whether the residual stream vector at that token is pointing a similar direction to that direction, or equivalently, depending on the dot product between the residual stream vector and the direction vector.

By observing which tokens light up blue and which tokens light up red, you can get a sense of what the direction is doing. For example, a direction that lit up early in the prompt in red and later tokens in blue would probably relate primarily to the positions of the tokens rather than their meanings. Finding interesting and interpretable directions is hopefully a good way to make interpretability progress.

How can we find interesting directions? One simple way of finding them is by running Principal Components Analysis, or PCA, on the residual stream vectors for a given layer. Basically, doing this automatically finds the most interesting directions for us, ranked in decreasing order of how interesting they are. You can look at directions like these using the "Component Index" dropdown. As a concrete example, if you look at Layer 0, Component Index 7, you'll be looking at residual stream vectors from the first layer, and you'll be looking at the eighth-most important "direction", as found by PCA. It's hard to know for sure, but it looks like that direction has at one of its ends auxiliary verbs like "is", "has", or "should", and has proper nouns at the other of its ends.

If you wanted to combine two or more directions, you could use the "Find a new direction" button. This will open a dialog box where you can find arbitrary linear combinations of PCA directions using the sliders. You'll be able to see the residual stream vectors update in real-time as you move the sliders. You can save those sliders and give them names and descriptions, and upvote descriptions for directions you like.

Any direction you save or description you give will be associated with your username. This website only requires a username--no password. This means that any other user can see what directions you've saved, simply by typing your username into the username field. Hopefully, that's a feature and not a bug, at least for now! Once you've saved a direction, you'll be able to view it by clicking it on the right side-bar.

You can also submit your own prompts. If you're curious about your theory of what a direction is doing, and want to test it, you could try submitting your own prompt and seeing if the pattern you've observed fits the prompt you've submitted.

Feedback/feature requests welcome! The more people use or engage with the tool, the likelier I am to continue working on it.