This was a project conducted during MATS 5.0 under the mentorship of Vanessa Kosoy and supported by a grant from BERI. It builds off the String Machines framework (and depends on the linked post for certain definitions), which models category-theoretic generalizations of finite-state transducers. [EDIT: The results here can also be found presented in self-contained form, in this paper.]
The framework as it previously existed did not have representation-independent ways of bounding (analogues of) time complexity, or natural guarantees that output size would not grow exponentially in input size. We introduce "filtered" transducers, which operate on categories enriched over filtered sets (sets equipped with a function to a partially ordered monoid, where morphisms are functions respecting order), and then, restricting our attention to transducers with a finite state space, prove constraints on the time complexity growth and expressivity of string machines.
Parameterizing complexity in string machines
Filtered transducers
Definition 1. The category of filtered sets is the category such that
- an object is a tuple , where is a set and is a function,
- a morphism is a function such that for all .
We will generally refer to objects in solely by the symbol corresponding to the underlying set going forward. One can observe that the identity function on a set by definition satisfies for all and is thus a morphism in . One can also observe that given and , for all , and therefore is also a morphism in . Therefore, is indeed a category.
Definition 2. Given two objects , we define their filtered product to be the set equipped with the function satisfying for all . Given a morphism and a morphism , we define the morphism to be the function . Indeed, we have that , so is a morphism in .
Due to the associativity and commutativity of addition, as well as the natural associativity and commutativity (up to isomorphisms which are still isomorphisms in ) of the cartesian product, is naturally associative and commutative up to isomorphism. Additionally, the one-element set equipped with and unitor maps which are the same as in (which are, by their definition, filtered morphisms) provides a left and right unit for , making a symmetric monoidal category.
Remark. Suppose filtered sets and filtered morphisms and . Then, the unique factoring function defined by is only a filtered morphism if , which does not hold in general. Therefore, does not provide a product except for when at least one of the sets has degree uniformly zero. However, does have finite products where . We will not be using this construction.
Remark. The set-theoretic disjoint union, with its degree function being the canonical factoring map to of its components' degree functions, provides all finite coproducts in .
Definition 3. A filtered-morphism category is a locally small symmetric monoidal category enriched over , using 's filtered product as its monoidal structure.
This expresses the notion of morphisms having degrees which are subadditive under composition in a way that naturally extends to a complexity constraint on transducers. As the monoidal identity of is the single-element set with degree zero, the arrows providing the identity morphism in the enrichment construction will ensure that identity morphisms are degree zero.
One can generalize the construction of by replacing with any partially-ordered symmetric monoid (where the partial order is, obviously, translation-invariant as it is with the usual definition of a partially-ordered group). We will make use of categories filtered over (with the partial order given by if and only if and ) in our construction of the filtered state category, as follows:
Definition 4. Given a filtered-morphism category and a list of -signatures (generators) and linear polynomials with coefficients in , the freely-generated -filtered category over with this list of signatures, or , is the symmetric monoidal category where:
- objects are exactly the objects of .
- A morphism is either a morphism of , or obtained by composing morphisms of with free generators added to for each -signature in the list.
- The -degree of a morphism is a linear polynomial with coefficients in , which is either its degree in (expressed as a constant) if it is a -morphism, the polynomial if it is one of the generators added when creating the category, or the sum of the degrees of all morphisms involved in its composition, with the degree contributions of composition-chains of -morphisms being the degrees in of the morphism they compose to, and these being strictly additive with each other and the degrees of any generator morphisms once all simplifications have been performed.
The monoidal product of a morphism with generators in its composition-chain and a -morphism is taken to have the sum of their -degrees.
We can now introduce filtered state categories.
Definition 5. Given a filtered-morphism category , its corresponding filtered state category is the category where
- an object is a tuple , where:
- The state space of is a set .
- The variables of are a functor from the discrete category corresponding to to the discrete category formed by all finite ordered tuples of pairs of objects in . We call the tuple associated with a given the variables at , or . Since variables implicitly denote morphism signatures, we will refer to a given variable as .
- The degree of a variable for some , denoted (or simply if can be inferred from context) is a tuple . We impose the same partial ordering on these tuples as we do with degrees in the freely-generated -filtered categories.
- a morphism of degree , where , is a tuple , where:
- The state transition is a function .
- The output function at , denoted , is a collection of morphisms in a freely-generated -filtered category over , defined as follows:
For each variable of degree , at , defines a morphism of degree at most (that is, the degree of the morphism cannot exceed this polynomial in either of its terms) in the freely-generated -filtered category over with generators and the degrees of those generators provided by the variables of degrees in . The function between hom-sets in can then be expressed by substituting each generator with a -morphism of the appropriate signature.
This induces a function (but not a filtered one!) between the product of the hom-sets for all variables at and the product of the hom-sets for all variables at , which can be obtained by replacing each generator corresponding to a variable at with a morphism of of the appropriate signature.- Given two morphisms of degree and of degree , their composition is a tuple where:
- The composite state transition is defined as .
- The composite output function is defined as follows: For each variable defined at , of degree , defines a morphism of degree at most in the category freely generated over with generators corresponding to the variables at and their degrees. Now, induces a functor from to (where denote the variables at ), which fixes but replaces every free generator of the category freely generated over the variables at with the morphism associated with it by , in the category freely generated over the variables at . Therefore, the output function at is simply the image of each of the morphisms generated by under this functor defined by . The function between products of hom-sets induced by the composite output function is therefore just the composition of the functions induced by the individual morphisms' output functions.
Now, for a given variable at of degree , every generator of some degree involved in the morphism of (initial) degree defined by has been replaced with one of degree . Suppose each generator appears with multiplicity in the morphism corresponding to . Then, we have it that , and since worth of degree has been added to the morphism for every generator appearing in it, we have that the degree of the morphism generated by must be . So, the degree of is .
Remark. is a filtered-morphism category with the degrees of morphisms being defined as in the definition of the category, as the identity morphism of each object has an output function that outputs a variable of degree (the generator corresponding to the variable itself) for any variable of degree and is thus of degree zero. Additionally, as also demonstrated in the definition, degree is subadditive with composition, meaning that the composition arrow is indeed a morphism in .
Definition 6. A filtered functor is an enriched functor between filtered-morphism categories.
Given a filtered functor , since the definition of an enriched functor requires the functor's action on morphisms to be provided by a morphism between hom-objects within the category, it automatically holds that for all morphisms in .
Definition 7. A filtered deterministic transducer is a deterministic transducer where the input and output categories, and , are filtered-morphism categories, and the functor affording the transducer structure is a filtered functor to the filtered state category of the output category.
Finite-state string machines
For the following section, we assume a filtered deterministic transducer with input category , output category , structure functor , input state space , output state space , primary input -signature , auxiliary input -signatures , and output -signatures . We will now demonstrate that requiring a finite output state space on a transducer provides us with certain output size and time complexity guarantees.
Proposition 1. If is finite, and, for every , the linear term of the degree of every variable in is nonzero, then, for every and every primary input -morphism , the number of copies of the generator corresponding to each auxiliary input appearing in each morphism corresponding to each output signature in is bounded by a fixed integer , which does not depend on .
Proof. Since is finite, and the number of variables which exist at any state is finite, there exists a variable with maximal linear degree across all variables in all states in , in some state in . No morphism in can generate a morphism in the appropriate -graded free category over with linear degree greater than that of its corresponding variable. Therefore, given any starting state , no morphism in exists where any component of the output function has more than copies of any of the generators corresponding to the variables at , since each of these will have sizes with linear term at least . ◻
Proposition 2. Suppose is finite, and every variable in every state in has a linear term of or greater in its degree. Denote the primary input morphism of as and its tuple of auxiliary input morphisms as , and define . Then, for every output signature , there exist fixed integers such that, for the morphism outputted for this signature given these inputs, .
Proof. For every output signature , there exists a state such that attains some maximal linear coefficient , the generators corresponding to auxiliary inputs of can appear in at most some fixed number of times. Additionally, a similar maximum can be found for the constant term of . Since, by the definition of a filtered functor, , and by the definition of the state category, the -degree of the output at can be at most , then . ◻
Corollary 2.1. Suppose a string machine composed only of a finite set of filtered transducers , where each transducer has input state space and output state space such that every variable at every state in has a degree with or greater linear term, and is finite. Denote by the morphism that will receive as its primary input morphism, given overall input morphisms and input states to the string machine. Then, .
Proof. Suppose two transducers , where receives a primary input morphism and auxiliary input morphisms . Therefore, by Proposition 2, there exist integers such that, for a given output produced by , the degree of satisfies . Now, if the primary input of is not connected to an output of , then the string machine composed of these transducers satisfies the proposition, as the inputs of are now included in the overall inputs of the string machine. If is composed into the primary input of , however, then . Given similar coefficients for a given output of , we can see that , where is bounded from above by either the same kind of linear sum as the one for (if the greatest degree among the auxiliary inputs comes from an output of ), or the degree of yet another additional input to the overall string machine. Therefore, any further composition of transducers will result in also being bounded by a linear sum of the degrees of the overall inputs of the string machine, meaning that the sum is also bounded by a linear sum of these degrees. ◻
Corollary 2.1 can be used to bound the time complexity of string machines, if, fixing some model of computation, we have a bound on the time it takes to run a single transducer as a function of its inputs. We note that the coefficients bounding output size are multiplied together upon composition into either an auxiliary input or a primary input, but only composition into a primary input ties the degree of the state transition that will occur in the second transducer to the primary input degree of the first transducer. We define the sum bounded in the corollary as follows:
Definition 8. Take a string machine with input signatures and input state spaces , where the transducers forming form the set . Denote by the morphism that the transducer will receive as its primary input morphism, given inputs ( for short) and ( for short) to . We define the internal total primary input degree of to be .
While we have established that, lacking a meta-vertex, will be linearly bounded by the total degree of its inputs, its scaling properties as a function of the number of transducers composed has no such guarantees. One can observe that composing more and more transducers that double their input size together causes exponential growth in . As we are interested in the time complexity of both string machines that incorporate a meta-vertex and of parameterized families of string machines, we must obtain some sufficient conditions for to grow polynomially in the number of transducers in our string machine. To help determine these conditions, we will define the output-degree-bounding parameters referenced in Proposition 2.
Definition 9. Take a filtered deterministic transducer with a finite output state space and an output signature of . Given an input state , primary input morphism , and auxiliary input morphisms to , denote by the output morphism produced for . We define the output degree of the output of to be the integer triple such that the relation described in Proposition 2, , holds for all possible and (and the produced by these inputs). Given the minimal linear term (at least ) that the degree of any variable in any state in the input state space of , and the maximal linear term and constant term for the degree of the variable in the output state space corresponding to , we can unambiguously define .
We can now prove some elementary sufficient conditions for for a family of string machines to grow polynomially in .
Proposition 3. Suppose a family of string machines , where is composed of a single filtered deterministic transducer with a finite output state space, and for , is created by composing some of the outputs of into the inputs of a new filtered deterministic transducer with a finite output state space, such that the remaining uncomposed input legs of each are the same for all . Given the output of composed into the primary input of the new transducer added to obtain , we designate the transducer that that output is produced from as , and write . Now, fixing any input states and morphisms, for some , regardless of the value of the inputs fixed, if the following conditions are met:
- We have that , for some fixed .
- We have that .
- The number of times that is .
Proof. Omitting our input morphisms and states, we have that , where is the output of composed into the new transducer's primary input. is obviously simply the degree of our initial primary input. either adds degrees' worth of material to the new transducer's primary input compared to , or at most multiplies by some fixed amount and then adds this extra degree. Since subsequent multiplications of this sum can be bounded from above by doing all the additions first first and then multiplying the result by the cumulative multiplication thus far, the function bounding can be expressed as a sum
where is the constant coefficient affording the bound, and is the total degree of the input morphisms to . ◻
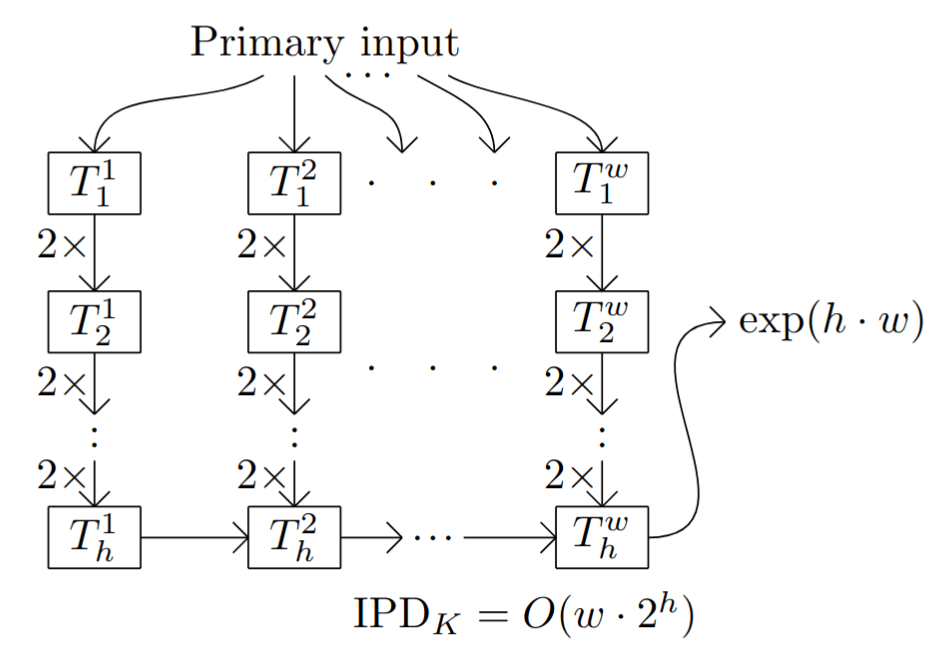
Remark. We have thus far only considered filtered transducers where the linear term of every variable in the input state space is non-vanishing. If we change this condition to only require that the constant term of the variable be non-vanishing, then the total number of generators in the -filtered category over the output category produced in the output is still bounded by a linear function of the primary input signature. So, the degree of the output function is now linear in the product of the degrees of the primary and auxiliary inputs. One can observe, however, that any composition of transducers will only cause outputs to be multiplied with each other a fixed number of times, so will now be bounded by a polynomial in the total inputs of the string machine.
String machine description length
As string machines can themselves be thought of as morphisms in a category, and we are interested in extending our complexity constraints to the case where the meta-vertex is involved, we must imbue the category that string machines are morphisms in with a filtered category structure itself. While this could be accomplished by setting the degree of a string machine to just be the number of transducers involved (where a no-transducer string machine is just the identity and has degree zero), this obviously fails to capture the internal complexity of a transducer.
If we require that the input category of every non-meta-vertex transducer be finitely-generated, then we could make reference to the size of some fixed graph representation of a transducer's transition table and output functions corresponding to generators, and then have this size be additive when transducers are composed. However, as discussed in the previous section, this description size does not constrain time complexity for transducers which build other transducers and then run them. We discuss possible approaches in our conclusion.
The expressivity of finite-state string machines
Now that we have obtained guarantees for the scaling of , which can be thought of as an analogue to the time complexity of running a string machine, in both the number of transducers in a string machine and in input size, we focus on characterizing the expressivity of string machines consisting of finite-state deterministic transducers, that is, filtered deterministic transducers where the state space corresponding to every element of the input category (not only the output state space) is finite.
In the following section, we will assume that all transducers have an input category that is of a form described as follows:
Definition 10. A tape category is a filtered-morphism copy-discard category freely generated over a single object and a finite number of morphisms of the form (where superscripts denote monoidal self-products), where every generator morphism has positive degree. If all our generator morphisms are of signature , then a tape category is the copy-discard category freely generated over the symmetric monoidal category freely generated from the multicategory with one object freely generated from those generators, by way of the functor from multicategories to monoidal categories proven by Hermida to be an adjoint to the forgetful functor in the other direction.
We can treat tapes as a special case of tape category, where all generators are endomorphisms of the generating object.
Without a meta-vertex
Finite-state string machines, even without a meta-vertex, can prepend to their output, which is not something the traditional definition of finite-state transducer can do. It is natural to investigate if this makes the framework more expressive than a deterministic finite automaton, e.g., having it recognize palindromes by reversing a string and then feeding the product of these two (their overlaying) into a transducer that then checks if each character matches up.
Unfortunately, given morphisms and in an input category (not necessarily a tape category) , and their product , we can see that, since , a state transition on a collection of finite state spaces induced by the product of two morphisms can only capture the same sort of information that could be captured by independently running two finite-state transducers on both morphisms and comparing their states at the very end.
Thus, "per-character" comparisons of the sort that would require conditions analogous to aligning characters on tape would require infinite state spaces to represent the equivalent memory operations being performed. However, due to the nature of the auxiliary input, as well as the aforementioned prepending capabilities, we are clearly able to model functions that finite state transducers cannot, even without a meta-vertex.
To characterize the class of decision problems computable by non-meta-vertex finite-state string machines, we first prove the following lemma:
Lemma 4. Suppose some finite-state transducer with primary input signature in a tape category , structure functor , and output state space , such that these are its only inputs and outputs. Fix a finite set of morphisms in the freely-generated -filtered category over with a single generating signature of degree , such that the linear coefficient of the degree of each is at most (that is, the generator corresponding to appears at most once). Suppose we are able to construct a primary input morphism for this transducer in the following way:
- Our starting value for is .
- We can replace with with one of the previously-given , with substituted for the generator morphism. We can perform this step a finite of times.
- Then, given some state transition reached as a result of some such , the space complexity of computing the output state of the transducer is in the degree of .
Proof. We will assume that one "computational step" involves performing one of the operations involved in constructing described above. We will demonstrate that computing the next state after any of the operations performed requires storing an amount of information that is in the degree of .
- If one of the does not have the generator morphism appear at all, then after this has replaced depends solely on the used, and since the set of such is finite, it takes a finite amount of space to store the state reached from the starting state when one of these are evaluated.
- If one of the only involves post-composing an endomorphism of into the generator, then storing the state reached from a given state after any of these endomorphisms is post-composed takes a fixed amount of memory, since the set of is finite.
- If one of the involves only pre-composing and post-composing endomorphisms of into , then computing the resultant state after the action of one of these only requires us to store extra "possible current states." That is, if we know what state we would be in after the evaluation of had we started at any other one of the states of the transducer, then after computing which new starting state we would have started at (which, since the set of endomorphisms we pre-compose is finite, is equivalent to storing a fixed-size transition table), we can then pick the state that the copy of the transducer that started at that state would be at after the action of . This is therefore equivalent to running copies of a finite state automaton, where each copy starts at a different state.
- Suppose one of the is obtained by taking a morphism , post-composing morphisms into each branch (such that one branch includes the generator), and then finally post-composing a morphism . Even if multiple "branchings" occur, since the generator where will be substituted appears only once, we can still decompose this into a morphism obtained by first taking the monoidal product of with a number of fixed morphisms such that the overall signature of their product is , and then composing in and . Now, we only need space to store the functions and induced by and , since these are functions between finite sets. Additionally, for the function induced by the monoid product of with with a fixed morphism of signature , by the property discussed at the start of this section, we only need to be keeping track of the action of on (which, since there are a finite number of , only requires keeping an absolutely bounded number of automata running), and then compute the action of on the result, which, as a function with a finite domain and codomain, takes finite space to store.
Therefore, to compute the state transition induced by , we only need to keep copies of the finite state automaton running, as well as some fixed number of finite-state automata with input and output state spaces corresponding to for some fixed . ◻
With this lemma, it now remains to show, roughly speaking, that for any string machine made out of finite-state deterministic transducers which decides some language (represented by morphisms in a tape category), the computation performed at every input morphism can be broken into a constant-bounded number of transitions of the type described in the lemma. We present a conjecture that finite-state string machines without a meta-vertex can only recognize regular languages, followed by a sketch for a proof of this conjecture.
Conjecture. Suppose a string machine composed only of finite-state transducers, where the input and output categories of each transducer are tape categories. Suppose this string machine has only one free input in some tape category where all generating morphisms (which form a set ) are endomorphisms of the generating object , and has as its sole output a state space , with some subset of designated as accepting. Then, taking an endomorphism in which does not include any instances of the copy morphism to be a string over the alphabet , any language over accepted by this string machine is regular.
Proof sketch. It suffices to prove that the computation involved in deciding this language takes constant space as a function of input size, as . More precisely, given any input morphism and a finite set of possible character strings that we can post-compose into , we desire to show that there is a constant-bounded amount of information (independent of the size of ) that we need to store, which will allow us to calculate the output state after any of these character strings are added to . By Proposition 1, each transducer involved in the string machine can create a constant-bounded number of duplicates of its auxiliary inputs within each of its outputs. This means that to predict the state of a given transducer after one of the operations described in Lemma 4 done to an auxiliary input, we need to store a constant amount of information. Moreover, due to the limitation caused by the size of a variable on the number of transitions one can make before we run out of variable space and must either limit ourselves to Lemma 4-like operations or reset, the number of "shapes" auxiliary inputs can exist in is absolutely bounded. The hope is that if we back-propagate until reaching the primary input of the first transducer, we will still have a constant-bounded amount of information to keep track of to predict the output state after the next character is reached.
Remark. This conjecture is already suggested by the combination of Corollary 2.1 and classical results by Kobayashi and Hennie which together imply that any one-tape Turing machine that runs in time decides a regular language. The reason the proposition is not trivially implied by these results is that a naive simulation of the string machine in question on a single-tape Turing machine will cross the last cell of its initial input a guaranteed times (when going back and forth to read the next cell to write the inputs to feed to the next automaton in line). The conjecture would also automatically be implied if we prove that the composition of two finite-state transducers can be equivalently modeled by a single finite-state transducer.
With a meta-vertex
The meta-vertex, even at meta-level one, can clearly be seen to increase the expressivity of finite-state string machines. We construct a string machine which can be recognize palindromes as follows:
Given a tape category where all generating morphisms are endomorphisms of the generating object , mark a special generating endomorphism . Given a generating endomorphism of , we define to be the filtered deterministic transducer with input and output category , with input and output signatures and three states, a fixed one of which is the starting state. When in the starting state, will transition to the "accepting state" and store in the sole variable at that state if it encounters , and transition to the "rejecting state" and store if any other generating morphism is encountered. When in the rejecting state, all morphisms are mapped to the identity on the rejecting state. When in the accepting state, all morphisms transition back to the accepting state, but this time append the current primary input generator morphism to the output. The end result is that when given an endomorphism , the transducer will output with its first "character" removed if and only if it starts with , and output otherwise. As a morphism, it is of signature .
Now, we define a filtered deterministic transducer with input category , which outputs a filtered deterministic transducer without meta vertices. This transducer has input signature and only one state, with one variable of signature , and it is assumed that no morphism fed to will include . Given a generator morphism of , the transducer will prepend to the current variable's stored string machine. If we compose a meta vertex that takes the output of and takes the same input morphism as and passes it on to the string machine formed by , then we obtain a string machine that outputs if it is given a palindrome, and if it is fed anything else.
Conclusions
Thus far, we have proven results about the time complexity and expressivity of finite-state deterministic transducers in the string machines framework. This framework allows us to model the compositionality of transducers in a way that allows for more compression of description length. For example, we are able to implement the trivial time-space tradeoff of recognizing a regular language that is the intersection of several regular languages by running several automata in sequence instead of the product automaton, or the cascade product in Krohn-Rhodes theory by having a transducer "shuffle" its primary input using its ability to prepend.
Additionally, our time complexity scaling guarantees in the number of transducers in a string machine translate to sufficient conditions for transducers which build and run other transducers in runtime to run in polynomial time. This will allow us to take advantage of the additional compression opportunities the meta-vertex presents. These results are valuable for developing string machines into a framework that can be used to model hypothesis spaces representable by automata.
Further work
Description complexity that encapsulates time complexity
As exemplified by Definition 4, the construction of filtered sets can be extended to a partially-ordered monoid that is not . Since a string machine without a meta-vertex will have the degrees of its outputs be bounded by a linear function of the degrees of its inputs, we can assign a degree to finite-state filtered transducers, where and are the maximal values for some sum of the coefficients appearing in the output degree in Definition 9, where the partial order is the same as in Definition 4. However, in this case, the monoid operation imposed on the polynomials is composition, due to how the linear relations bounding output size get composed when transducers are composed, and the filtered-set category is no longer symmetric monoidal since this operation is not commutative.
Now, the variables in our state categories would have their degrees be of the form , where a morphism of degree can compose in a transducer of at most that degree, meaning the output variable is of degree by abuse of notation. where the superscript indicates -fold self-composition. At further meta-levels, we keep adding terms, though it is unclear how we would disambiguate which variable to compose into for the monoid operation.
Characterizing the expressivity of transducers with a meta-vertex and monadic transducers
We have not yet established bounds on the expressivity of finite-state deterministic transducers which incorporate the meta-vertex, but, due to the bounding on levels of meta, it is likely that the languages they decide are some subset of context-free languages. The time complexity guarantees also need to be translated to the monadic case. Work on bounding the expressivity of monadic string machines may involve defining equivalents for string machines of various properties (see work by Mohri, Allauzen et al., Kostolanyi, and Bell et al.) which characterize determinizable weighted transducers, which may in turn allow us to bound the computational complexity of computing the distribution on output morphisms given by a monadic transducer.