This is the first post in a sequence of posts summarizing Rationality From AI to Zombies.
Rationality, probability theory, and decision theory
Some words are hard to define, but you still have a good sense of what they mean. I've always felt like that about the term "rationality". In describing it to friends, sometimes I'd fumble around and say that it kinda combines a lot of academic fields like statistics, behavioral economics, philosophy, and AI. But really, I think it's just about doing (and believing) what makes sense.
In a broad sense, not a narrow one. As a programmer, I may study relational databases, but that's not what rationality is about. Relational databases is too narrow of a topic for rationality. It's only something I could apply to programming. It's not something I could apply to, say, making dinner. But the planning fallacy can be applied to making dinner, and to bike rides, and the NBA draft, and job hunting, and relationships. It can be applied generally. It's not limited to a specific domain. There are exceptions, but rationality is usually interested in these sorts of more generally applicable ideas. The more generally applicable, the more powerful.
There are a lot of misconceptions about rationality, which basically strawman it as being ultra logical and dismissive of things like intuition, emotions, and practicality.
Hollywood rationality is a popular stereotype of what rationality is about. It presents "rationalists" as word-obsessed, floating in endless verbal space disconnected from reality, reciting figures to more decimal places than are necessary, or speaking in a dull monotone. Hollywood rationalists also tend to either not have strong (or any) emotions. When they do, they often do not express them. Needless to say, this has nothing to do with actual rationality.
Think Spok from Star Trek. This of course is silly. A few posts in the book talk about these strawmans, but I don't really think it's worth discussing further.

Well, there's one thing I want to call out: you don't have to be really good at math to understand rationality. It's something that should be accessible to the average Joe. In practice, there is a little bit of math thrown around, but it's usually pretty accessible. On the other hand, sometimes Eliezer (and other authors) explain things in an overly complicated and/or technical way (he acknowledges this in the preface). But that's not a problem inherent to rationality. Rationality is something that can — and should! — be made simple.

Let's return to my somewhat circular idea that rationality is about doing what makes sense. I am fond of this idea, but the book framed it in a different, more precise way that I also thought was really cool.
Rationality can be broken down into two things: 1) epistemic rationality, and 2) instrumental rationality. Epistemics are about beliefs and instrumental is about actions. It's the difference between having an accurate map of reality and being able to use that map to steer reality in the direction you want it to go.
I think we need some examples. Believing that Apple's stock will fall due to Covid is a question for epistemic rationality. Believing that putting your money in an index fund in a "set it and forget it" matter is the best way for you to achieve your goals of getting a good return on your investment while also being happy, as opposed to, say, day trading part time — that's a question for instrumental rationality. It's a question of how to achieve your goals. How to win.
That's a great term: "win". Rationality is ultimately about winning.
But the distinction between epistemics and instrumental rationality feels very fuzzy to me when you really examine it. The instrumental question of how to manage your finances, it ultimately just comes down to epistemic questions of belief, right? I believe that it is highly unlikely that I could beat the market by trading. I believe that doing so would take up a lot of my time and make me unhappy. I believe that I have better things to do with my time. So when you factor out the instrumental question, doesn't it just get broken down into epistemic components?
This book doesn't get into all of this fuzziness, it just starts you off with what I feel like is more of a hand wavvy description. But here's my stab at addressing the fuzziness. I'm assuming that we should make decisions based on expected utilities. But what if we instead should use something like Timeless Decision Theory (TDT) to make decisions. Then it becomes a matter of more than just epistemics. Two people can agree on the epistemics and disagree on what the right action is if they disagree on what decision theory should be used.
I can't think of an example of this other than Newcomb's problem though. But I don't understand other decision theories very well. It's not something that I know a whole lot about. It seems to me that maximizing expected utility works quite well in real life but that other decision theories are useful in more obscure situations, like if you're building an AI (a super important thing for humanity to learn how to do). For now, I think that most of us could squint our eyes, use expected utility maximization as our decision theory, and look past the fuzziness between epistemics and instrumental rationality. If I'm wrong about any of this, please tell me.
Something that I thought was cool is that probability theory is the academic field that studies epistemics, and decision theory is the field that studies instrumental rationality. It feels like a nice way of framing things, and it had slipped my mind for a while.
Oh, by the way: within the realm of probability theory, Bayesians are the good guys and frequentists are the bad guys. More on this later. Bayesian probability is a big deal.
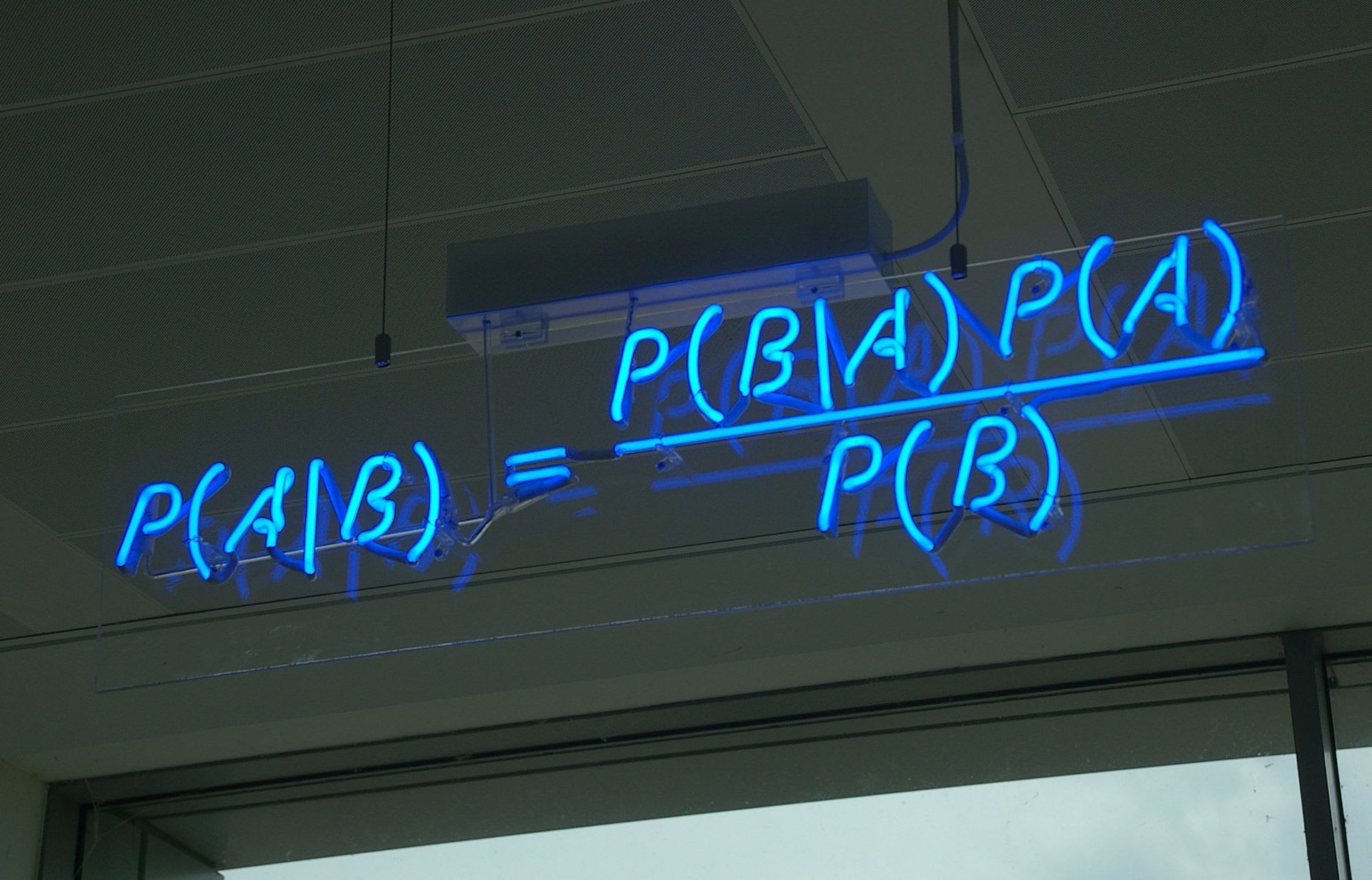
I'm not sure who the good and bad guys are in decision theory.
Cognitive biases
You've seen an optical illusion before, right? You can't always trust your senses! Isn't that crazy? You literally can't believe your eyes.
Well, I like to think of cognitive bias as a cognitive illusion. Your brain might tell you that dinner will only take 20 minutes to make, but that's as much of an illusion as a Necker cube. You can't always believe your own eyes, and you can't always believe your own brain.
There are some subtle differences between the two, but let's start off thinking about it this way and perhaps address the differences in the future. In short, the difference is that with a bias you're leaning in the wrong direction, eg. towards overconfidence, but with an illusion you're just wrong, not necessarily wrong in a particular direction.
You might be thinking: if we're wrong in a particular direction, eg. towards being overconfident, can't we just adjust in the opposite direction? Yes! Yes we can! Eliezer uses the phrase "the lens that sees it's own flaws".
Imagine an optical illusion where things that are far away appear to be closer. Humans are smart enough to figure this out and adjust. "The ball looks like it's 20 feet away but it's probably more like 45". We have scientists that have studied vision, and eye doctors to tell us when our vision is off so that we can make these sorts of adjustments.
Similarly, think of the planning fallacy as a cognitive illusion. Things that take a long time appear to take a shorter amount of time. Humans are smart enough to figure this out and adjust. "It looks like dinner will take 20 minutes but it's probably more like 45." We have scientists who study and discover cognitive biases like these, and we have bloggers to spread the word and inform us.
In practice, it's actually a lot harder than it sounds to make these sorts of adjustments. I'm not sure why. Humans are weird.
One thing that is helpful is to do belief calibration training. You could also do a less formal version of that. Just revisit old beliefs, reflect on your track record, and think about the mistakes you've made in the past. Eg. perhaps with PredictionBook.
Here's an example of something even more informal. When the NBA draft rolls around each year, I like to try to predict which players will be good. For the past six years I've been ranking players and writing out a few paragraphs of my thoughts for each player. Then I go back, see how I performed, see what errors I've made, and try to adjust and avoid those errors in the future. For example, I've had a tendency to underestimate young players. A 19 year old has a lot more room for growth than a 21 year old, but I've had a tendency to underestimate just how large of an effect this is.
In addition to discussing the general idea of biases, Eliezer has a few posts that talk about a specific bias. The planning fallacy, scope insensitivity, availability heuristic, conjunction fallacy, and a few more. That is just the very tip of the iceberg though. There are so many more! Check out this Wikipedia page, or the canonical book by Kahneman and Tversky, Thinking Fast and Slow.
Guys, our brains are broken! We have to learn about the ways in which they are broken so that we can adjust!
Real beliefs
Real beliefs are about predictions.
I think that this is the overarching idea behind the Fake Beliefs and Mysterious Answers sections. Let me explain what I mean.
First, let's consider the classic parable of a tree falling in a forest with no one around to hear it. Did it make a sound? Alice says of course. Just because no one was there doesn't mean it would change course and not make a sound anymore. But Bob questions this. How could it make a sound if no one was there to hear it?
The issue is that they are using different definitions of the term "sound": "acoustic vibrations" and "auditory experience". But do Alice and Bob actually believe different things? No! They both predict that the air molecules vibrated. And neither predicts any subjective auditory experience, aka "hearing". So no, they don't believe different things. Beliefs are predictions, and they are both predicting the same consequences of the tree falling.
Note that Eliezer talks about anticipated experiences instead of predictions. There may be some subtle differences, but these differences don't seem important, and "predictions" is more intuitive to me, so that's the term I'm going to use.
One edge case worth noting is that even if you can't observe something directly with your senses, you can still have a proper belief about it. For example, you can have a belief about how two atoms interact even though you can't see them with your naked eye. You can see them with a microscope, and you can make predictions about what would happen under a microscope when they collide.
This all may seem pretty obvious. Of course beliefs are about predictions. What else would they be about? Well, Fake Beliefs and Mysterious Answers each provide numerous examples.
The best one is probably belief in belief. And I think that hell is a great example of belief in belief.

"Hell?" said the calm voice of the Defense Professor. "You mean the Christian punishment fantasy? I suppose there is a similarity."
Imagine believing that if you had sex before marriage, that you'd go to hell. Ie. that when you die, you'll burn and be tortured throughout eternity! I don't know about you, but if I actually predicted that as the consequence of my having sex before marriage, well, I'd never consider it even in my wildest dreams! More generally, I'd also be pretty neurotic all of the time about avoiding other types of sins.
I don't think I'm alone here. And yet, people who "believe" in hell go about their lives without this neuroticism.
I can only conclude that hell is a fake belief. People who believe in hell don't actually predict that eternal torture will be the consequence of them having sex before marriage.
So then, what exactly is going on? Well, maybe they're just professing. "Hey guys, look at me, I'm a good Christian. I'm saying the right things." They think it's all BS but don't want to be excluded from the group.
That's one hypothesis. That they're lying through their teeth when they say they believe in hell. But maybe that's not what's happening.
Maybe they don't think that hell is a bunch of BS. Maybe they... believe... that they believe in hell. If you ask them, they'll tell you that they believe in hell. If there was such thing as a true lie detector test, they would pass. But at the same time, they don't actually predict eternal torture as the result of them having sex before marriage.
"How on earth would that be possible? Those two thoughts totally contradict each other."
Look, I totally get it. I'm right there with you. It's definitely weird. I think Eliezer undersold just how weird of an idea this is. But humans are weird, and we actually have inconsistent thoughts all of the time. From what I understand, psychologists call it compartmentalization. Take the first thought, tuck it away in a compartment. Take the second thought, tuck it away in a compartment. The thoughts contradict one another, but since they're siloed off in their own compartments, they're "protected" from being destroyed by the contradiction. That's my hand wavvy, amateurish understanding anyways.
Another example of a fake belief is something Eliezer refers to as cheering. Imagine someone who is a strong proponent of gun rights. They say it just isn't the governments place to tell citizens they can't have guns. Period. End of story. It doesn't matter what age the person is. Hell, start 'em early, that's what I say! Six years old. I don't care. And shit, better not restrict me to puny pistols. No, I want automatics! For myself, and my six year old! The government better not tell me no! And they shouldn't have restrictions for felons, or the mentally ill. That's not their place. Or restrictions about where I can and can't bring my gun. If I want to bring it inside a bank, I should be able to do that. Honestly, I love guns. I think that everyone should have one. Man up! Let's all put on our big boy pants and arm ourselves!
Does this person actually believe that a mentally ill six year old with behavioral problems should be able to run around a library with an uzi? Probably not. In the above paragraph, they weren't actually meaning all of that stuff literally. They were just cheering. "Yay guns! I'm a strong believer in guns!" To express how pro-gun they are, they went over the top.
If you're interested other types of fake beliefs, check out the other posts in the section. If you're content with this "beliefs are predictions" idea, read on.
In the Mysterious Answers section, the posts largely revolve around a concept called fake explanations. But fake explanations are pretty closely related to fake beliefs, so the way that I see it, fake beliefs is the larger, overarching idea. The umbrella.
To understand what a fake explanation is, consider the following story. A physics professor shows his students a metal plate next to a radiator. The students touch it and find that the side closer to the radiator is cold, not hot, and it's the other side far from the radiator that is hot. Why is this?
The true reason is simply because the professor flipped the plate without the students noticing. But "heat conduction" is what the students answered.
Ok... but what does "heat conduction" mean?
Do you expect metal near a heat source to be cold because of heat conduction? No? You expect it to be hot? No? It depends? Depends on what? How do you expect heat conduction to work? What do you predict (there's that word again) will happen as a result of heat conduction? If you can't answer those questions, then "heat conduction" isn't actually an explanation. You're just saying words. Making sounds with your mouth.
Sorry, I don't want to be mean. But like Eliezer, fake explanations frustrate me. They feel dishonest, and perhaps manipulative. If you don't know how to explain something... then say you don't know. Just admit it. Don't make sounds with your mouth in hopes of getting a gold star.
Ouch, that was sassy. Sorry. I'll start being nicer now.
A proper explanation has to make predictions. It has to stick it's neck out. "Heat conduction" has to predict the near side to be either hot or cold. Or, if it depends, then you have to say what it depends on, and follow up with a prediction. If it depends on X, you can say "if X = 1 it'll be hot and if X = 2 it'll be cold". Something like that. You just can't avoid sticking your neck out. You have to say something that has a chance at being wrong.

Eliezer likes to frame this a little differently. He says that if "heat conduction" can explain it being hot just as well as it being cold, then it can't actually explain anything. That your strength as a rationalist is to be more confused by falsehood than by truth. That way of framing has always felt awkward/confusing to me though.
This is a great segue into Guessing The Teacher's Password. Imagine a student choosing "heat conduction" as an answer on a test. The student doesn't know anything about how heat conduction works — he wouldn't be able to use it to make predictions eg. about whether a metal square will be hot or cold — but he remembers the teacher talking about it in class with an example that feels similar to the one on the test. So he guesses that the answer is "heat conduction".
A lot of students have knowledge that is restricted to this form. "When the teacher asks me something like this, I recite back the answer." Such knowledge is extremely fragile. It breaks down when you are asked questions that deviate from the ones your teacher asks you. Y'know, like in the real world!
On the other hand, when you deeply understand something and it's Truly A Part of You, you'd be able to regenerate it if it were deleted from your memory. For example, consider the Pythagorean theorem: . Personally, I just have it memorized and I know how to use it, but it's not truly a part of me. If someone deleted that line from my memory, I wouldn't be able to regenerate it. But someone like Eliezer who truly understands it would be able to regenerate it through their knowledge of math and through the deeper principles underlying the theorem, even if the specific line was deleted from his memory.
Is there anything I understand deeply enough that I'd be able to regenerate it? The example that comes to mind are pot odds. Pot odds are a thing that poker players talk about. Imagine that the pot is $10 and someone bets $5. Now the pot has $15 in it and you have to put in $5 if you want to have a chance at winning. You're risking $5 to win $15. That risk-reward ratio of are the pot odds, and you can use it to make decisions as a poker player.
There was a point where I had a shallow understanding of pot odds. I just did what the books told me to do, using pot odds how they said to use it. But eventually I realized that pot odds are just a short cut for expected value calculations. A crude shortcut with some important flaws. At this point, if you deleted the concept of pot odds from my memory, I'd be able to regenerate it through my understanding of expected value (and my understanding of the importance of devising shortcuts that are easy enough to use in real time during poker games).
Of course, in practice there's a big space on the spectrum between Guessing the Teacher's Password and Truly A Part of You. It's not one or the other. Don't worry if you're not quite at the Truly A Part of You extreme all of the time.
Fake explanations have always felt like something that happens more in real life than fake beliefs. And sure enough, Eliezer provides some real world examples of it. Examples from mainstream scientific opinion, not weird religious things like hell.
In particular, the ideas of emergence and complexity. What's the difference between these two sentences:
1. Intelligence is an emergent product of neurons firing.
2. Intelligence is a product of neurons firing.
If the answer is "nothing", then emergence would be functioning as a fake explanation. It isn't... adding anything to the story. Consider these questions:
1. What predictions would you make if it were an emergent product?
2. What predictions would you make if it were an "ordinary" product?
You'd make the same predictions in both cases, right? If so, "emergence" is a fake explanation.
Again, it's worth noting that this is an error happening frequently within mainstream scientific opinion (consensus?), in the year 2020. It's not a fringe thing that only stupid people are vulnerable to.
It's also worth noting that some people might use the term emergence in such a way that is a real explanation, not a fake one. For example, consider a related idea: that the internet will "wake up" and become an AI once there is sufficient complexity. That seems like an advanced prediction to me. If emergence is a thing you predict that it will "wake up". If emergence isn't a thing, you predict that it will not "wake up". I think these predictions are in violation of reductionism and determinism, so I think that the explanation is wrong, but that doesn't mean that it's not real. Being real is only about actually sticking your neck out and making predictions. About the possibility of being wrong. It doesn't matter if those predictions are illogical.
It's bad enough that someone giving a fake explanation isn't actually sticking their neck out and allowing themself to be wrong. On top of this, their explanation often serves as a curiosity stopper.
"Why are humans intelligent?"
"Emergence."
"Oh ok. But how does that work?"
"Shh! Stop trying to analyze it. You're ruining the beauty!"
Here's another example:
"Why are leaves green?"
"Science."
"Oh ok. Cool!"
Science is supposed to be about exploring how things work, but all too often it acts as a curiosity stopper instead. Aka a semantic stop sign. "When you see this word, stop asking questions." Clearly the person who answered "science" was trying to signal that there is nothing further to discuss.
I wanted to follow up with more examples of fake explanations and curiosity stoppers, but I can't really think of any. It'd be great if people would post examples in the comments. In the book, Eliezer spends time talking about the examples of elan vital and phlogiston, but personally, I don't like those examples. Because they are confusing, and because I'm not sure if they actually are fake explanations, depending on how charitable you want to be.
Bayesian evidence
To me, the Noticing Confusion section is all about the idea of Bayesian evidence. I'm not really sure why it's labeled "Noticing Confusion".
Anyway, Bayesian evidence. One of my favorite things to talk about. The way I like to think about it, Bayesian evidence is anything that moves the needle. If it shifts your beliefs at all, it counts as Bayesian evidence.

I think the best way of understanding this is in contrast to other definitions of evidence, like scientific evidence or legal evidence (or what police officers consider to be evidence). Scientists arbitrarily use the cutoff. If , the results of the experiment don't count and get thrown away. The scientific community doesn't incorporate those results into their beliefs.
Why on earth would they do that? I don't quite understand, but I do know that it's for social reasons. As opposed to... mathematical ones, I guess you can call it. I think the institution of science wants to only include things that we feel really confident on. Otherwise, there may be confusion about what's true and what isn't true. Or maybe the issue is that if science included things that weren't known, there would be public incidents where science turned out to be wrong, and then people stop trusting scientists. Perhaps the institution of science wants to avoid these situations, and thus decides to set the bar high for what it decides to count as evidence.
Again, I don't have the best understanding of this, and there are a lot of justifiable gripes to be had with the institution of science, so maybe they're just doing it all wrong, but regardless, the point relevant to the discussion here is that social institutions may have reasons to use different criteria for determining what is and isn't evidence. However, be very careful not to confuse scientific evidence with Bayesian evidence. They are talking about different things, and if you confuse them, the consequences could be tremendous.
For example, consider this story about a big shot oncologist. The patient was doing well after chemo and is going to the doctor to see if it's worth getting more chemo to kill off the last bits of cancer that still remain. Common sense would say there is a trade-off of killing off the cancer versus dealing with side effects, and that a doctor would be able to help you navigate these trade-offs most effectively. But the doctor claimed that there is no evidence that getting chemo would do any extra good in this scenario.
Huh? How could that be? Well, the problem is that the doctor is confusing scientific evidence with Bayesian evidence. Perhaps there haven't been (enough) studies on this specific situation that have passed the critical threshold. Perhaps there is no scientific evidence. But that doesn't mean there is no Bayesian evidence. C'mon, do you really think that chemo does zero extra good?
Consider a similar situation. There is "no evidence" that parachute use prevents death or major trauma when jumping out of airplanes. Are you going to throw away your parachute?
The lesson here is that you have to be smart about when to incorporate Bayesian evidence. You can't only focus on scientific evidence and throw everything else away. If you do, you'll start jumping out of airplanes without parachutes, and telling cancer patients that chemo does nothing. The former is silly, but the latter is a real world situation that happens all the time due to people making this error and treating non-scientific evidence as "unholy".
Here's another important, real world situation where people dismiss Bayesian evidence in an effort to be Good Scientists and it leading to death and suffering: the early days of the coronavirus pandemic. Have you ever seen Covid described as "nCoV" or "novel coronavirus"? I'll explain why that happens. There have been many coronaviruses in the past. This is just the most recent one. That's right, it's not the coronavirus, it's a coronavirus. SARS and MERS were also coronaviruses.
This is very good news. Coronaviruses all share similarities with one another. We can use what we know about other coronaviruses to make inferences about how this novel coronavirus will behave. For example, that it will be seasonal and that masks will reduce spread.
Unfortunately, the world failed to do such things. Why? Because there was "no evidence". People were looking for proper scientific studies to be done before we assume something like "masks reduce transmission". The error here is to focus on scientific evidence while dismissing Bayesian evidence. Our knowledge of how other coronaviruses behave was pretty strong Bayesian evidence that this one would be similar. And for something like wearing masks, the cost is low, so we don't need to set the bar super high. We can start wearing masks even if we're only moderately confident that they work given how cheap and practical they are. Perhaps there are other situations that call for a higher bar where we may need to focus more heavily on scientific evidence, but this was not one of them.
Ok, so to recap, Bayesian evidence is anything that moves the needle, there may be social reasons to use different criteria for evidence in some contexts, but in those cases it's still important to understand the difference between those criteria and the more "foundational" Bayesian evidence. Actually, not only what the differences are, but when it is appropriate to use which definition of evidence.
I like "moves the needle" as an intuitive and handwavvy explanation, but let's dive a little deeper into what it actually means for something to count as Bayesian evidence. Or in other words, what is it, exactly, that allows you to move the needle?
To answer that question, imagine that you are trying to figure out whether or not you have Covid. You wake up one morning, and your nose is a little stuffy.
It's probably nothing. It could easily just be a normal cold. A stuffy nose isn't even one of the big indicators of Covid. Maybe you just left the window open and the room was colder than normal. A stuffy nose seems trivial. It shouldn't count as evidence, right?
Well, does it move the needle? Even just a little bit? More specifically, in worlds where you have Covid, how likely is it that you wake up with a stuffy nose? And in worlds where you don't have Covid, how likely is it that you wake up with a stuffy nose? The answers to those questions will tell you whether or not it counts as Bayesian evidence. Whether it moves the needle at all.
If the answers are literally exactly as likely, then in that case, no, it doesn't count as Bayesian evidence. It doesn't help you move the needle. But if one is even slightly more likely than the other, then that allows you to move the needle, and it does count as Bayesian evidence.
Getting more general, to figure out whether something is Bayesian evidence, ask yourself how likely the observation is in worlds where your hypothesis is true, and how likely it is in worlds where it's false. That general description has always hurt my brain a little bit though. I like to think about specific examples.
Here's a specific example. I was watching John Oliver today and he talked about how things like a poll worker eating a banana isn't evidence of voter fraud. But is that actually true? What do you think?
It certainly isn't strong evidence. If it is evidence, it surely is very weak evidence. But... are we sure that it doesn't move the needle at all? Because that's what has to happen for it to not be evidence at all.
What questions do we have to ask ourselves? 1) In worlds where someone is committing voter fraud, how likely are they to be eating a banana? 2) In worlds where someone is not committing voter fraud, how likely are they to be eating a banana? I would probably guess that 2 > 1, with my underlying model being that people who commit such fraud would be too tense to eat. So I'd interpret it as pretty weak evidence against voter fraud.
The point I was going for here is that it'd usually pretty hard for something to not move the needle at all. In this case the banana eating probably moves us slightly away from the voter fraud hypothesis, but it'd be unlikely for something even as trivial as eating a banana to not move the needle at all.
Anyway, that's how to think about what it means for something to count as Bayesian evidence. I don't want to imply that we should be spending our time thinking about what bananas say about voter fraud. Often times in practice things that barely nudge the needle can be safely ignored, or at least heavily de-prioritized. So then, we are interested in how much an observation actually moves the needle. To figure that out, we need Bayes' Theorem!

I'd really, really recommend reading through Arbital's guide on Bayes' Theorem. It's absolutely fantastic. But I'll still give a quick explanation.
I find the odds form of Bayes' theorem way more intuitive and easy to think about than the other forms. Here's how it works. You start off with a prior probability (or prior odds, since we're using the odds form). Suppose the prior odds of you having Covid are . Then you observe that you woke up with a stuffy nose. How much more likely are you to make that observation in worlds where you have Covid than in worlds where you don't?
Maybe it happens 50% of the time when you have Covid and 10% of the time when you don't. This gives you a likelihood ratio of . You take that likelihood ratio and you multiply and to get 5 and 50 or posterior odds of . See how the left hand side of the prior odds, likelihood ratio and posterior odds all correspond to having Covid? The posterior odds tell you that for every 1 time you do have Covid, there are 10 times where you don't, so there is a 1 in 11 chance overall that you have it.
I really love the odds form of Bayes' Theorem. I remember when I came across it in Arbital's guide. It was a lightbulb moment for me. "Ah, now this finally makes sense!" I don't know why it isn't more popular. It really, really seems like it should be. It's amazing how simple and easy to use it is.
This is a great example of what I was saying in the beginning about the math that rationalists need to know not actually being difficult. The Hufflepuff inside me envisions a future where the odds form is taught in schools and actually becomes a normal part of our culture.
Why do I like it so much? Well, remember when we talked about what the definition of rationality is? Epistemic rationality was one part. In some sense, it's the overwhelmingly dominant part if you wave your hands and say that we'll just use expected utility maximization as our decision theory. Well, probability theory is what informs epistemic rationality. And Bayes' Theorem is the big dawg in probability theory. It is the thing that allows us to update our beliefs and figure out how the world works. In as broad and general a way as possible. It doesn't just help us in some situations, it helps us in all possible situations. "How do you figure out X? Just use Bayes' Theorem!" Guys, this right here, this is it!

Ok, I'm exaggerating a bit about it's usefulness. People don't actually go around using Bayes' theorem in day to day life, or even their jobs most of the time. Not even superforecasters. Why? The same reason why I don't calculate expected value at the poker table: it would take too long, and it often isn't even clear how I'd go about doing so. Humans need simplification and shortcuts. That's why Bayes' Theorem doesn't actually prove to be a tool we use frequently.
But, it's still the thing that underlies everything else, which is useful to know about, eg. by helping you to find the right shortcuts. I also just find it tremendously elegant for there to be a single, relatively simple equation that is basically the answer to the question "How do I figure out what is true?"
Bayes' Theorem may seem like just a simple equation, but it has implications that reach into fields like philosophy. There's a whole class of implications about how the institution of science violates principles of Bayes' Theorem. One that I think is particularly important is that you can't just test whatever hypothesis you want.
You see, in the institution of science, it's a sin to believe a hypothesis if the results of an experiment go against that hypothesis. You aren't allowed to believe whatever you want, you have to follow the data.
Fair enough. But when you're still at the "generate a hypothesis" stage, science let's you do whatever you want. Generate whatever wacky hypothesis you can think of. Sure. We don't care. As long as you test it experimentally and abide by the results of the experiment.
But here's the thing: before generating the hypothesis, Bayes' Theorem gives you an answer to the question of how likely that hypothesis is to be true. Maybe it's 30%. 5%. 0.01%. Whatever. So then, it would be silly to go around testing implausible hypotheses over more plausible ones (all else equal). Why not favor the most plausible ones? Again, maybe the answer is for social reasons of providing researchers with autonomy and letting them have fun. But for you as a rationalist trying to do what makes sense, you should get rid of the idea that you could just choose whatever hypotheses you want. No, you should choose the plausible ones. The ones that make the most sense.
The way Traditional Rationality is designed, it would have been acceptable for me to spend thirty years on my silly idea, so long as I succeeded in falsifying it eventually, and was honest with myself about what my theory predicted, and accepted the disproof when it arrived, et cetera. This is enough to let the Ratchet of Science click forward, but it’s a little harsh on the people who waste thirty years of their lives. Traditional Rationality is a walk, not a dance. It’s designed to get you to the truth eventually, and gives you all too much time to smell the flowers along the way.
Luck
As I wrap up the summary of this book, I realize that I didn't address some posts. I just couldn't find a good place to fit them. But there's one point that I feel the need to make, one that hits close to home for me.
There's a saying in the LessWrong community that "incremental increases in rationality don't lead to incremental increases in winning". Eliezer talks about this in My Wild and Reckless Youth:
When I think about how my younger self very carefully followed the rules of Traditional Rationality in the course of getting the answer wrong, it sheds light on the question of why people who call themselves “rationalists” do not rule the world. You need one whole hell of a lot of rationality before it does anything but lead you into new and interesting mistakes.
...
The Way of Bayes is also an imprecise art, at least the way I’m holding forth upon it. These essays are still fumbling attempts to put into words lessons that would be better taught by experience.
...
Maybe that will be enough to cross the stratospherically high threshold required for a discipline that lets you actually get it right, instead of just constraining you into interesting new mistakes.
I think a simpler way to say this would be to just call it luck.
By leveling up as a rationalist, you increase your skill. And that's great. But success happens in large part due to luck as well, so being really skilled is hardly enough to make you successful. You have to be really lucky too.
Well, that's not necessarily true. It is possible to reach such a tremendously high level of skill that the luck part of the equation goes away, and you can just own the results.
Poker comes to my mind as an example. The best poker player in the world very well might lose to a complete amateur in any given game. There is a lot of luck in poker, otherwise the fish wouldn't stay around. You need a crazy large sample size to shave off the impact of luck.
But is luck inherent in the game of poker? I don't think so. If you can successfully "soul read" your opponent, you can usually find a path that leads to them folding and you winning the hand.
No one can actually do this. The best players in the world often put their opponent on a wide range of possible hands. But, if we're talking about the ceiling of how high a poker player could possibly climb, I at least suspect that luck could be eliminated for all intents and purposes.
And I share that same suspicion for rationality. Right now the "level of our game" is low enough where we can't use our skill to reliably win. There's still a lot of luck involved. But, down the road, I think we can develop the ability to do the equivalent of "soul reading". To have such an incredibly high level of skill where reality truly is at our mercy.
I need to raise the level of my game.
That was the thought Harry was looking for. He had to do better than this, become a less stupid person than this.
I need to raise the level of my game, or fail.
Dumbledore had destroyed the recordings in the Hall of Prophecy and arranged for no further recordings to be made. There'd apparently been a prophecy that said Harry mustn't look upon those prophecies. And the obvious next thought, which might or might not be true, was that saving the world was beyond the reach of prophetic instruction. That winning would take plans that were too complex for seers' messages, or that Divination couldn't see somehow. If there'd been some way for Dumbledore to save the world himself, then prophecy would probably have told Dumbledore how to do that. Instead the prophecies had told Dumbledore how to create the preconditions for a particular sort of person existing; a person, maybe, who could unravel a challenge more difficult than prophecy could solve directly. That was why Harry had been placed on his own, to think without prophetic guidance. If all Harry did was follow mysterious orders from prophecies, then he wouldn't mature into a person who could perform that unknown task.
And right now, Harry James Potter-Evans-Verres was still a walking catastrophe who'd needed to be constrained by an Unbreakable Vow to prevent him from immediately setting the Earth on an inevitable course toward destruction when he'd already been warned against it. That had happened literally yesterday, just one day after he'd helped Voldemort almost take over the planet.
A certain line from Tolkien kept running through Harry's mind, the part where Frodo upon Mount Doom put on the ring, and Sauron suddenly realized what a complete idiot he'd been. 'And the magnitude of his own folly was at last laid bare', or however that had gone.
There was a huge gap between who Harry needed to become, and who he was right now.
And Harry didn't think that time, life experience, and puberty would take care of that automatically, though they might help. Though if Harry could grow into an adult that was to this self what a normal adult was to a normal eleven-year-old, maybe that would be enough to steer through Time's narrow keyhole...
He had to grow up, somehow, and there was no traditional path laid out before him for accomplishing that.
The thought came then to Harry of another work of fiction, more obscure than Tolkien:
You can only arrive at mastery by practicing the techniques you have learned, facing challenges and apprehending them, using to the fullest the tools you have been taught, until they shatter in your hands and you are left in the midst of wreckage absolute... I cannot create masters. I have never known how to create masters. Go, then, and fail... You have been shaped into something that may emerge from the wreckage, determined to remake your Art. I cannot create masters, but if you had not been taught, your chances would be less. The higher road begins after the Art seems to fail you; though the reality will be that it was you who failed your Art.
It wasn't that Harry had gone down the wrong path, it wasn't that the road to sanity lay somewhere outside of science. But reading science papers hadn't been enough. All the cognitive psychology papers about known bugs in the human brain and so on had helped, but they hadn't been sufficient. He'd failed to reach what Harry was starting to realise was a shockingly high standard of being so incredibly, unbelievably rational that you actually started to get things right, as opposed to having a handy language in which to describe afterwards everything you'd just done wrong. Harry could look back now and apply ideas like 'motivated cognition' to see where he'd gone astray over the last year. That counted for something, when it came to being saner in the future. That was better than having no idea what he'd done wrong. But that wasn't yet being the person who could pass through Time's narrow keyhole, the adult form whose possibility Dumbledore had been instructed by seers to create.
Questions for readers
I have some questions for you:
- I've bought in to The Church of Bayes. On the other hand, I'm not seeing how decision theory is important aside from situations like building an AI or weird hypotheticals like Newcomb's problem. Any insight?
- Who are the "good guys" and "bad guys" in the field of decision theory? Or is that not a good way to think about it?
- Can you think of any good examples of fake beliefs or fake explanations? I spent a few Yoda timers on it but wasn't able to come up with much.
- Continuing that thought, do you find the ideas of fake beliefs and fake explanations useful? Have you caught yourself falling prey to either of them?
- Continuing that thought, is it useful to spend time understanding mistakes that other people make even if you yourself are unlikely to make them? Because my impression is that LessWrongers probably don't make the mistake of fake beliefs too often, in which case I ask myself why the idea is useful.
- Am I underestimating the wisdom of scientific evidence being used instead of Bayesian evidence?
- Are you able to think about the probability form of Bayes' rule intuitively? I can only think intuitively about the odds form. Any pointers for how to think about the probability form intuitively?
- Why is the Noticing Confusion section called that? To me it seems like it's all about Bayesian evidence.
- Is it fair to call the ideas in the last section "luck"? If not, is "luck" at least close to being accurate?
- What were the biggest takeaways you got from these posts?
- How would you group together the posts? R:AZ used "Predictably Wrong", "Fake Beliefs", "Noticing Confusion" and "Mysterious Answers".
- I left out Occam's Razor because I don't have a great understanding of it. It seems to me like it's just the conjunction rule of probability, but that people maybe misuse it. P(A) might be less than P(B & C & D & E & F) if B, C, D, E, and F are all really large. So what is the big takeaway? That "and" drives the probability down? What are some good examples of where this is useful?
- Have you found it useful to think about bits of evidence?
Those are just the ones that come to mind right now. Other comments are more than welcome!