Here are some updates on the work that @Jeremy Gillen and I have been doing on Natural Latents, following on from Jeremy's comment on Resampling Conserves Redundancy (Approximately). We are still trying to prove that a stochastic natural latent implies the existence of a deterministic latent which is almost as good.
First, if a latent is a deterministic function of X and Y, (ie. ), the deterministic redundancy conditions will be satisfied up to errors of and H(X|Y). (We don't actually use this in anything that follows, but think its quite nice.)
Proof:Proof
First, write out using the entropy chain rule:
Since is a deterministic function of X and Y, we can set .
We can expand differently using the entropy chain rule.
The two expressions for must be equal so:
.
Re-arranging gives:
We can repeat this proof with X and Y swapped to get the bound
Furthermore, we can always consider a latent which just copies one of the variables (for example ). This kind of latent will always perfectly satisfy one of the deterministic redundancy conditions (if , then ). The other deterministic redundancy condition will be satisfied with error . The mediation condition will also have zero error since (since ).
We can choose to copy either or , meaning that using this method we can always construct a deterministic natural latent with
Another deterministic latent that can always be constructed is the constant latent This will always perfectly satisfy the two deterministic redundancy conditions, since . The mediation error for the constant latent is just the mutual information between and .
Between these two types of latent, a deterministic natural latent can always be constructed with error bounded by . Loosely: if and are highly correlated you can use the copy latent and if and are close to being independent, you can use the constant latent.
To test how tight this bound is, Jeremy has numerically found the optimal deterministic and stochastic natural latents for a family of (X,Y) distributions. The distribution is parametrised by which captures how correlated and are ( implies perfect correlation and implies no correlation). A nice graph of these results is below:
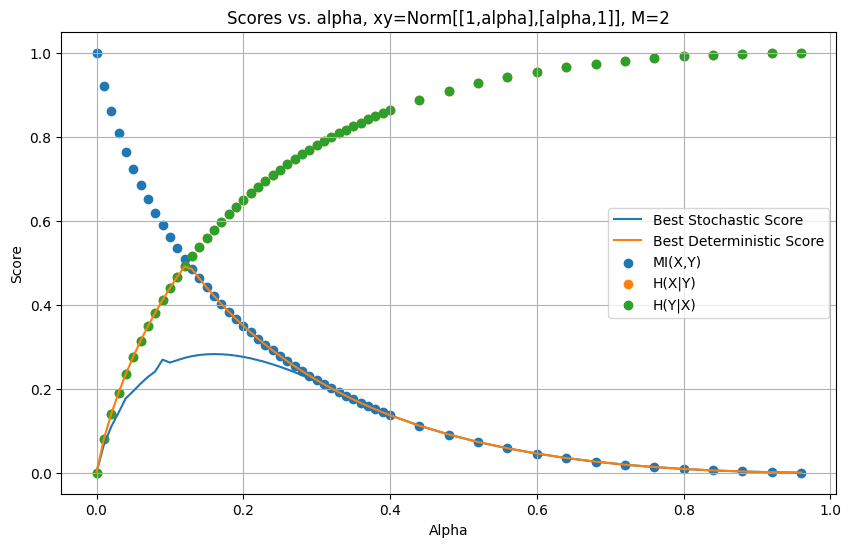
The ‘score’ of the latents is the sum of the errors on the mediation and redundancy conditions. The fact that the best deterministic score closely hugs the line suggests that the bound we found above is pretty tight. When we look at the latents found by the numerical optimizer, we find that it is using the copy latent at low and the constant latent when.
We also have a graph which breaks down the individual errors for optimal stochastic and deterministic latents:
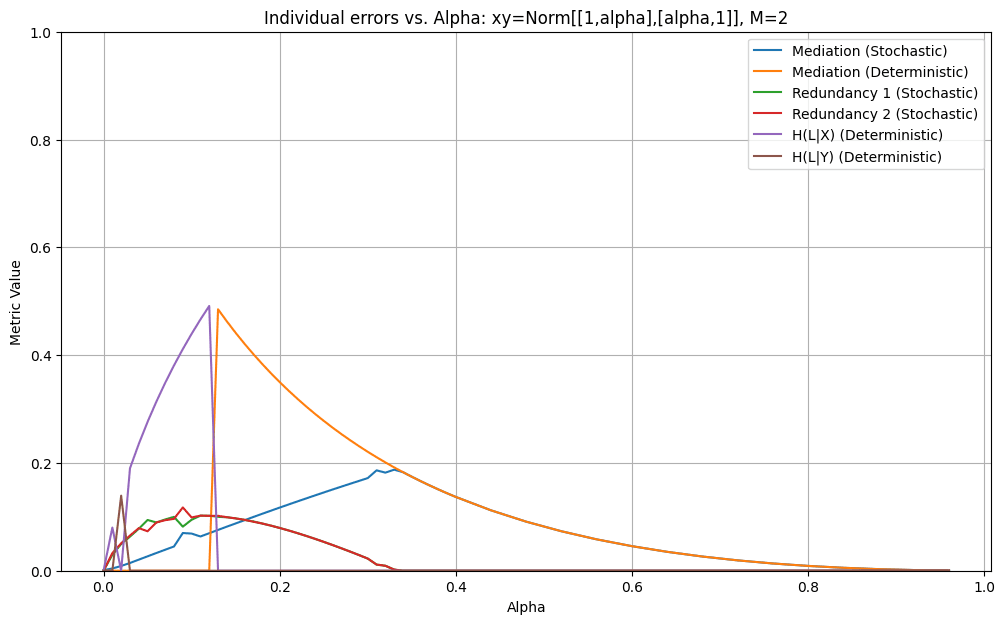
It shows quite clearly the point where the optimal deterministic latent switches from ‘copy’ to constant around . Furthermore, for we have shown that the constant latent is at a local minimum in the space of possible stochastic latents. We did this by differentiating with respect to the conditional probabilities and finding the Hessian. This was done using a symbolic program so we don’t have a compact proof to put here. The point is also the point where the errors for the best stochastic and deterministic latents become the same. This seems like good news for the general NxN conjecture, since it shows that when two states are roughly independent, there’s zero cost (to the difference between stochastic and deterministic scores) to ‘merging’ those states from the perspective of the latent.
Eyeballing the first graph, it seems like the deterministic score is never more than twice the best stochastic score for any given distribution. It is interesting to note that the optimal stochastic latent roughly follows the same pattern as the deterministic latent but it notably performs better than the deterministic latent in situations where both and are high. Bear in mind that these graphs are just for one family of distributions (but we have tested others and got similar results).
At the moment we are thinking about ways to lower bound the stochastic latent error in terms of and . For example if we could show that it is impossible for a stochastic latent to have a total error less than then this would prove that the existence of a stochastic latent with error implies the existence of a deterministic latent with error or less. We are also thinking about ways to show that certain latent types have errors which are global minima (as opposed to just local minima) in the space of possible latents.
That sounds about right. The extra thing that they are claiming is that these assumptions are things that naturally apply in real life, when a controller is doing its job (ie. they are not just contrived/chosen to get the result). So (Wonham et al claim) the interesting thing is that you can say that these isomorphisms hold in actual systems. Obviously there are a bunch of issues with this. I intentionally avoided too much discussion and criticism in this post and put it in a separate post.
Thanks for your comment. I am glad the post helped you!
Good questions. The short answer is that you are correct and I was sloppy in that section.
Could the evolution of the joint states form a cycle?
Yes! In fact, if S and W are finite sets then the evolution must eventually form a cycle. (If a finite set S has cardinality n, you can only apply a function at most n times before you return to a state you have visited before). I meant this to be implicit in the '... etc.' part but I didn't make it clear. I have added the following sentence to the post which hopefully clarifies things:
If the sets and are finite with cardinality then the evolution would eventually cycle around so we would have to specify that the evolution will eventually come full circle ie. and .
Could multiple joint states evolve to the same joint state?
This is a good question involving a subtlety that I skipped over. The answer is 'yes sometimes'. But when it does happen its a little weird and worth thinking about. There are a few ways ways in which multiple joint states could evolve to the same joint state.
1)Two different environment states with the same controller state evolving to the same environment state. eg. and
In this case, the Detectability condition is violated, since the controller will do the same thing, regardless of whether the environment is in and . The Detectability condition would tell us that this means that s_1 and s_3 are (from the point of view of the controller) identical, so we should coarse grain them so that they are both labelled the same. This means that we wouldn't expect this kind of joint evolution.
2)Two different controller states with the same environment state lead evolve to the same joint state. eg and
In this case, Detectability is satisfied. As far as I can tell, this kind of evolution does not violate any of the conditions for the IMP so it is valid. However, notice what this would imply. There are two controller states (w_1 and w_3) which both do the same thing to the system (cause it to evolve to s_2). After either of these states, the controller then evolves to w_2 and from then on behaves identically forever. It seems to me that for our purposes w_1 and w_3 are 'the same' controller state so I would be inclined to coarse grain them and label them as the same, removing this kind of evolution. However, since there are no assumptions which explicitly require this kind of coarse graining over the controller states, this kind of evolution is technically allowed within the IMP.
3)Two joint states with different environment and controller states evolve to the same joint state. eg. and .
Again, I think that this is allowed within the IMP. But notice that after the evolution both trajectories will behave the same. This means that if the environment and controller state sets are finite then at most one of these joint states will be involved in any kind of repeating cycle. The other will be 'transient' ie. it will occur once and never again.
I think that reading the whole soliloquy makes my reading clearer and your reading less plausible. I can maybe see that if you:
- Ignored the whole context of the rest of the play
- Ignored the lines in the soliloquy which specifically mention the family names
- Ignored the fact that there is a convention in English to refer to people by their first names and leave their family name implicit
Then maybe you would come to the conclusion that Juliet has an objection to specifically Romeo's first name and not the fact that his name more generally links him to his family. But if you don't ignore those things, it seems clear to me that Juliet is lamenting the fact that the man she loves has a name ('Romeo Montague') which links him to a family who she is not allowed to love.
I strongly agree with the general sentiment of ‘don’t be afraid to say something you think is true, even if you are worried it might seem stupid’. Having said that:
I don't agree with your analysis of the line. She’s not upset that he’s named Romeo. She is asking “Why does Romeo (the man I have fallen in love with) have to be the same person as Romeo (the son of Lord Montague with whom my family has a feud)?”. The next line is ‘Deny thy father and refuse thy name’ which I think makes this interpretation pretty clear (ie. if only you told me you were not Romeo, the son of Lord Montague, then things would be ok). The line seems like a perfectly fine (albeit poetic and archaic) way to express this.
This works with your modern translation ("Romeo, why you gotta be Romeo?"). Imagine an actor delivering that line and emphasising the ‘you’ (‘Romeo, why do you have to be Romeo?’) and I think it makes sense. Given the context and delivery, it feels clear that it should be interpreted as 'Romeo (man I've just met) why do you have to be Romeo (Montague)?'. It seems unfair to declare that the line taken out of context doesn’t make sense just because she doesn’t explicitly mention that her issue is with his family name. Especially when the very next line (and indeed the whole rest of the play) clarifies that the issue is with his family.
Sure, the line is poetic and archaic and relies on context, which makes it less clear. But these things are to be expected reading Shakespeare!
It is also fairly common for directors/writers to use a book as a inspiration but not care about the specific details because they want to express their own artistic vision. Hitchcock refused to adapt books that he considered 'masterpieces', since he saw no point in trying to improve them. When he adapted books (such as Daphne du Maurier’s The Birds) he used the source material as loose inspiration and made the films his own.
François Truffaut: Your own works include a great many adaptations, but mostly they are popular or light entertainment novels, which are so freely refashioned in your own manner that they ultimately become a Hitchcock creation. Many of your admirers would like to see you undertake the screen version of such a major classic as Dostoyevsky’s Crime and Punishment, for instance.
Alfred Hitchcock: Well, I shall never do that, precisely because Crime and Punishment is somebody else’s achievement. There’s been a lot of talk about the way in which Hollywood directors distort literary masterpieces. I’ll have no part of that! What I do is to read a story only once, and if I like the basic idea, I just forget all about the book and start to create cinema. Today I would be unable to tell you the story of Daphne du Maurier’s The Birds. I read it only once, and very quickly at that. An author takes three or four years to write a fine novel; it’s his whole life. Then other people take it over completely. Craftsmen and technicians fiddle around with it and eventually someone winds up as a candidate for an Oscar, while the author is entirely forgotten. I simply can’t see that.
FT: I take it then that you’ll never do a screen version of Crime and Punishment.
AH: Even if I did, it probably wouldn’t be any good.
FT: Why not?
AH: Well, in Dostoyevsky’s novel there are many, many words and all of them have a function.
FT: That’s right. Theoretically, a masterpiece is something that has already found its perfection of form, its definitive form.
AH: Exactly, and to really convey that in cinematic terms, substituting the language of the camera for the written word, one would have to make a six- to ten-hour film. Otherwise, it won’t be any good.
(From Hitchcock/Truffaut, quoted here).
Alfonso Cuaron also liked the idea of Children of Men (the book) but disliked almost all the specific details, so he used his film as a chance to make all of the changes he wanted to see.
In the post 'Can economics change your mind?' he has a list of examples where he has changed his mind due to evidence:
1. Before 1982-1984, and the Swiss experience, I thought fixed money growth rules were a good idea. One problem (not the only problem) is that the implied interest rate volatility is too high, or exchange rate volatility in the Swiss case.
2. Before witnessing China vs. Eastern Europe, I thought more rapid privatizations were almost always better. The correct answer depends on circumstance, and we are due to learn yet more about this as China attempts to reform its SOEs over the next five to ten years. I don’t consider this settled in the other direction either.
3. The elasticity of investment with respect to real interest rates turns out to be fairly low in most situations and across most typical parameter values.
4. In the 1990s, I thought information technology would be a definitely liberating, democratizing, and pro-liberty force. It seemed that more competition for resources, across borders, would improve economic policy around the entire world. Now this is far from clear.
5. Given the greater ease of converting labor income into capital income, I no longer am so convinced that a zero rate of taxation on capital income is best.
6. The social marginal value of health care is often quite low, much lower than I used to realize. By the way, hardly anyone takes this on consistently to guide their policy views, no matter how evidence-driven they may claim to be.
7. Mormonism, and other relatively strict religions, can have big anti-poverty effects. I wouldn’t say I ever believed the contrary, but for a long time I simply didn’t give the question much attention. I now think that Mormonism has a better anti-poverty agenda than does the Progressive Left.
8. There are positive excess returns to some momentum investment strategies.
I don't know enough about economics to tell how much these meet your criteria for 'I was wrong' rather than 'revised estimates' or something else (he doesn't use the exact phrase 'I was wrong') but it seems in the spirit of what you are looking for.
I know you asked for other people (presumably not me) to confirm this but I can point you to the statement of the theorem, as written by Conant and Ashby in the original paper :
Theorem: The simplest optimal regulator R of a reguland S produces events R which are related to the events S by a mapping
Restated somewhat less rigorously, the theorem says that the best regulator of a system is one which is a model of that system in the sense that the regulator’s actions are merely the system’s actions as seen through a mapping h.
I agree that it has nothing to do with modelling and is not very interesting! But the simple theorem is surrounded by so much mysticism (both in the paper and in discussions about it) that it is often not obvious what the theorem actually says.
The diagram is a causal Bayes net which is a DAG so it can't contain cycles. Your diagram contains a cycle between R and Z. The diagram I had in mind when writing the post was something like:
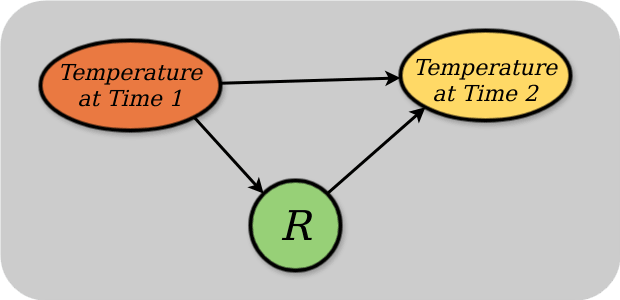
which is a thermostat over a single timestep.
If you wanted to have a feedback loop over multiple timesteps, you could conjoin several of these diagrams:
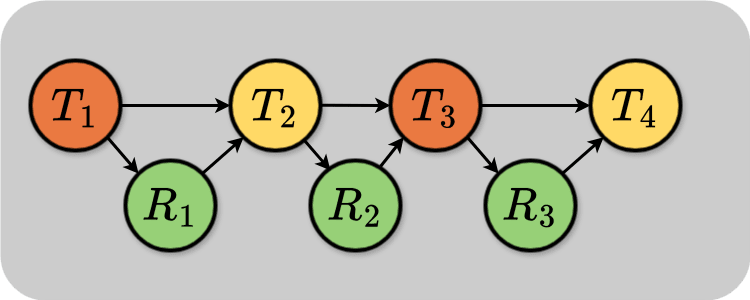
Each node along the top row is the temperature at successive times. Each node along the bottom row is the controller state at different times.
Hi, Jeremy and I have a couple of updates on this thread. I have put them in a shortform here.