This post was written during the Dovetail Research Fellowship. Thanks to Alex, Dalcy, and Jose for reading and commenting on the draft.
This post assumes that you are familiar with the Abstract Internal Model Principle (IMP). In a previous post, I wrote what I hope is a fairly straightforward explanation of the IMP so if you are not familiar with it, I recommend you start with (or at least skim) that post before reading this one. If you want more mathematical details, I also recommend Jose's posts on the IMP.
I was interested in the IMP because I wanted to know if it could be considered a selection theorem. A selection theorem is a result which tells us something about the structure of system, given that certain behaviours are selected for. In particular, in Agent Foundations, we are interested in circumstances under which 'agent-like structure' is selected for. By 'agent-like structure', we normally mean 'having a world model and a search process', along with some kind of value representation. Understanding the circumstances in which agent-like behaviour (or powerful optimisation) lead to agent-like structure is a problem often referred to as the 'Agent-like Structure problem'.
The author of a paper on the IMP describes it as showing that "a feedback regulator must incorporate a dynamic model of its environment in its internal structure"[1] which sounds a little bit like a useful selection theorem. Being an effective feedback regulator is a bit like being an optimizer (in a broad sense) and 'incorporating a dynamic model of the environment in the internal structure' sounds a lot like 'having a world model'. So, I (along with @Alex_Altair and @JoseFaustino) have been wondering if, through some small tweaks, the IMP could be modified to be a selection theorem of the form 'an optimizer must contain a world model in its internal structure'.
Unfortunately, doing this is not super straightforward. The IMP has several issues which mean that it doesn't naturally transfer over to the setting of the Agent-like Structure Problem. This post is a list of areas where the IMP falls short of being a selection theorem for agent-like structure, along with suggestions as to how it could be modified to be more applicable to the Agent-like Structure Problem. I think that writing this post has been pretty valuable to me and helped me clarify some criteria that a useful selection theorem would have to satisfy, even if the IMP fails to satisfy them.
But before the suggested improvements, I'll give a list of things I like about the IMP.
Things the IMP Gets Right
First, I think that the proof of the Abstract IMP (which I outlined in a previous post) is correct. As far as I can see, the mathematical reasoning is solid and the conclusions follow from the premises. In this regard, when I'm criticising the IMP, I'm not saying it is 'wrong', just that it doesn't apply to the Agent-like Structure Problem in the way that I would like it to.
Second, there is a version of the IMP, which I'll refer to as the Linear IMP (as opposed to the Abstract IMP) which is framed in the language of linear differential equations and control theory. This version does seem to describe regulators which are 'useful' and appear in control theory. Of course, there is a difference between a result that can describe useful systems and the result itself having useful applications. But I can believe that the original IMP holds in a wide range of useful control systems. Furthermore, Wonham (the author of both the original IMP paper and the Abstract IMP) implies that the Linear IMP is a special case of the Abstract IMP. I haven't verified this, but if it this is true, then it means that the Abstract IMP also holds in these systems.
Third, I quite like the notion of a 'model' used by the IMP. In the Abstract IMP, the model is captured by an isomorphism between the controller and the environment. The punchline of the IMP is that there is an injective (one-to-one) function which maps between controller states and environment states. The controller evolves autonomously and in such a way that one can predict the evolution of the environment state by only looking at the controller state. In this sense, the controller 'models' the environment. Results like the Good Regulator Theorem assume that the environment is an i.i.d random variable and say that the controller must be a deterministic function of this variable. In some ways, the IMP notion of a 'model' improves on this, since it leads to the controller being dynamic model of the environment. Not only does the controller model what state the environment is in, it also models how it evolves. Unfortunately, the notion of a model used in the IMP is flawed in other ways, as I'll discuss later.
So, why isn't the IMP a good selection theorem for agent-like behaviour? I'm going to give a few suggestions for how one could improve the IMP to make it more relevant to the Agent-like Structure Problem. These are avenues which we are currently exploring, so this should be read as more of a speculative research agenda, rather than a list of results.
Note that a lot of these are slightly different ways of getting at similar issues, so this list might seem repetitive.
How to Improve the IMP
1) Relax the Assumption of Autonomy
The proof of the IMP rests on the so-called 'Feedback Structure Condition' which stipulates that the controller is autonomous while the system remains within the set of 'good' or 'desired' states [2].
This means that, while the system remains in the set of 'good states' the controller will evolve in such a way that (the controller state at time ) depends only on (the controller state at time ) and not on any details of the environmental state at time .
The motivation for this assumption comes from the standard feedback regulator model of control theory:
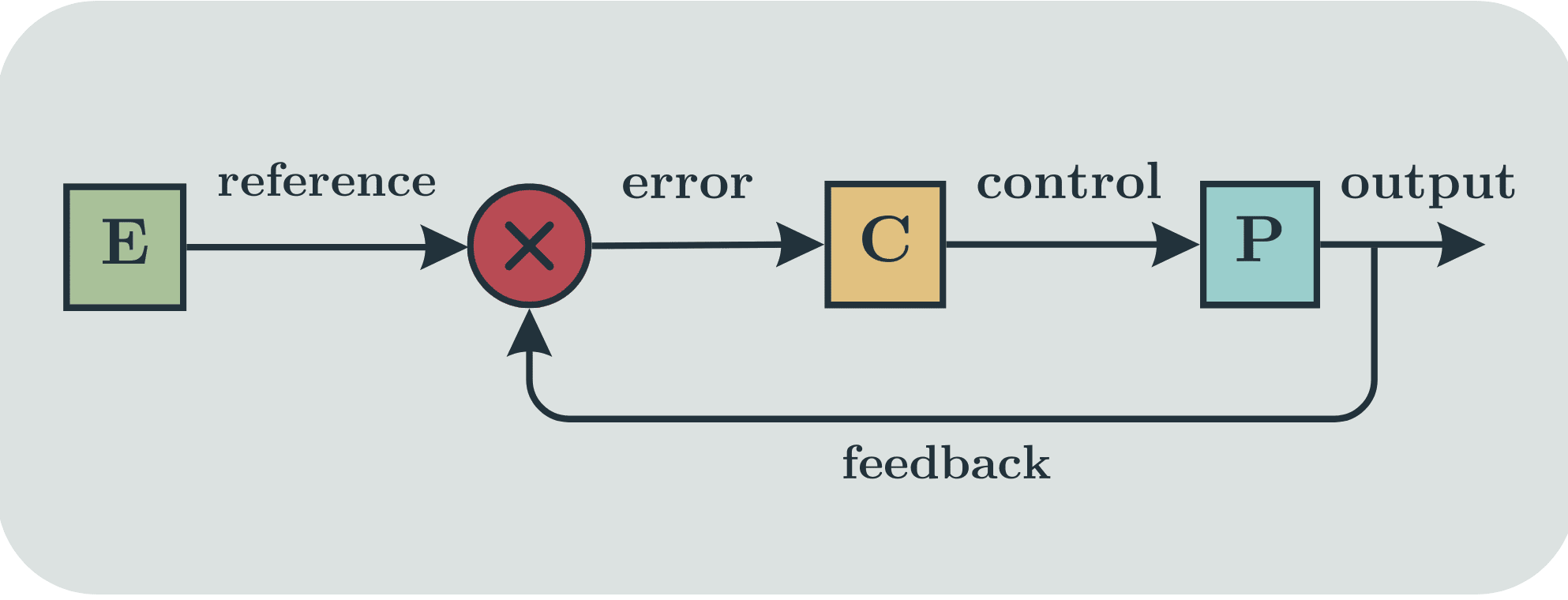
Here, the input which the controller takes is the difference between the plant output and the exosystem input (compared through some 'reference' function). This generates an 'error tracking signal' which captures information about how far the plant is from being 'good' compared to the exosystem signal. If the system is in a good state, then the error tracking signal is zero and the controller receives no input. This means that, within the good set of states, the controller must evolve autonomously.
While I understand the motivation behind this assumption, it is not clear that it applies more generally to agents or optimizers. It seems perfectly possible for a controller to be constantly correcting its state based on 'observations' from the outside world (and thus not being autonomous) while also staying within a set of 'good' states. Indeed, my understanding is that this is what actually happens in many control systems. The tracking error never completely reaches zero, it just becomes small, and the error going to zero is an idealisation in the limit .
The assumption that the controller is autonomous within the good set of states seems less important to me than the requirement that the controller is not autonomous outside of the good set of states. After all, being not autonomous outside of the good set of states is what allows the controller to steer the system back into the good set.
Its possible that this is not an insurmountable problem when trying to adapt the IMP to be a selection theorem. One could introduce a coarse-graining to the system which treats 'small' errors as being 'zero' and 'approximate controller autonomy' as 'full controller autonomy'. But it isn't clear to me that you can do this for all systems. Surely there are systems (perhaps systems that are chaotic in some hand-wavy way) where rounding off small errors to zero eventually compounds and causes bigger changes in other parts of the system? And even doing this doesn't account for systems that continually update their internal state based on observations. Modifying the IMP to include non-autonomous controllers would be a step towards describing a wider range of agent-like behaviour.
2) Introduce a causal link between World and World Model
When I think of agents having world models, I have some notion that there will be an isomorphism between the external world and the internal states of the agent, which is indeed captured by the IMP. But this isn't all. There is also a causal element: if I make a change to the external world, I expect the agent's internal world model to update accordingly. But the IMP notion of the controller 'modelling' the world is purely correlational. Indeed, this needs to be the case because the IMP requires that the controller is autonomous. Therefore, the only kind of modelling it can do is correlational. Everything in the IMP is deterministic and there is no room for causal interventions that are not already accounted for by the dynamics (as captured by ).
To give an example, imagine two clock faces, Clock A in Aberystwyth and Clock B in Brighton. If they are both working correctly and telling the correct time, there will be an isomorphism between their states. In this sense (which is the sense used in the IMP), Clock A will be a model of Clock B (and vice versa). But there is no causal sense in which Clock A is modelling Clock B. If I perform an intervention on Clock B by, say, manually adjusting the hands or throwing a hammer at it, those changes will not automatically manifest in Clock A. This two-clock setup satisfies the conditions of the IMP, but the notion of Clock A 'modelling' Clock B lacks this robustness to interventions and adaptability which we might expect in agents.
3) Make it harder to Satisfy the Conditions
If we want to use the IMP as a selection theorem, we need to have some criteria which tell us 'this system is exhibiting agent-like behaviour'. Unfortunately, the conditions used in the IMP are quite weak and cover a wide range of behaviours, including behaviours which we would not consider 'agent-like'. If we want to make the IMP a selection theorem, we would need to make the bar for 'agent-like behaviour' higher, so as to rule out pathological not-agent-like behaviours which nonetheless satisfy the conditions of the IMP.
I realised halfway through writing that this concern has already been raised by Imran Thobani in this paper. The concern is that you can apply the IMP to a very broad class of systems and show, with an appropriate level of coarse graining, that they satisfy the IMP assumptions and therefore one is 'modelling' the other. This can be done even the system doesn't match with our intuitive notion of 'modelling' or look anything like a control system. I'll explain this criticism in more detail using an example from Thobani's paper, reproduced in my own words.
Imagine a radioactive rock sitting by the seaside. Since the rock is radioactive, its internal state can be used as a 'clock' which tells us what the time is (up to an accuracy of, say, 1 hour). This is because radioactivity will predictably decay so by measuring the activity, and comparing it to the initial activity at the start of the day, you can work out how much time has passed. As a result, we can coarse-grain the 'radioactivity' variable so that it just tells us how many hours have passed since the start of the day. In fact, (for reasons which will become clear later) we will coarse-grain the radioactivity variable so that it only tells us whether an even or odd number of hours has passed since the start of the day. Call this variable , and let it take values EVEN or ODD depending on how many hours have passed. Also, we will specify the rock's location using a variable which can take one of two values: BEACH or SEABED. The state of the rock at any given timestep will be characterised by the pair . The rock will be our 'controller' even though (spoiler alert) it doesn't do much in the way of 'control'.
In this example, the 'environment' variable tells us about the waves at the beach. Assume that, each hour, a wave hits the beach. There are two kinds of waves: HIGH and LOW and they follow a predictable pattern, alternating each hour between HIGH and LOW. We will denote the hours passed since the start of the day using the variable . So if the wave is HIGH at time , it will be LOW at time .
At time , the first wave hits the beach. If the wave is HIGH, the rock gets flung high up on the beach, so its -state becomes . The rock is flung with such force that it is now out of reach of any further waves, so it will remain with indefinitely. If, on the other hand, the first wave at is LOW, the rock will get pulled down to the seabed, where it will stay indefinitely, unaffected by future waves. This means that all future states of the rock will have .
If the rock's state is the controller and the wave state is the environment, then we can see that this example satisfies the assumptions of the IMP. The Feedback Structure Condition is satisfied, since, after , the rock evolves autonomously. The Detectability Condition is also satisfied, since at any time the environment state can be inferred by looking at the controller state. This is because the waves follow a predictable pattern. If , then the first wave (at ) was HIGH, meaning that the wave state will be HIGH at , etc. and LOW at ,etc. Alternatively, if , then the wave state will be HIGH at and LOW at . Thus, the environment state can be inferred by the variable , along with whether is odd or even, which is exactly the information that is captured in the variable .
Therefore, we have an environment and controller which are both autonomous and there exists a bijective function between them. In other words, there is a one-to-one correspondence between the rock's internal state and the wave state. In this sense, we can use the IMP to claim that the rock is 'modelling' the waves.
This seems like a powerful criticism of the IMP, since the rock isn't doing what we would normally think of as 'modelling', nor is it behaving like a 'controller' or an 'agent'. It is simply passively correlated with the external world. Thobani argues that we can construct examples like this in almost any situation where the controller contains a 'clock', since many well-defined environmental dynamics can be mapped in a one-to-one fashion onto an appropriately coarse-grained 'time' variable. A 'clock' is just any system from which the time can be deduced (in the above example, the role of the 'clock' is taken by the radioactivity of the rock).
Of course, we haven't shown that every situation where the IMP applies leads to spurious identifications of 'modelling'. Just that it is very easy to conclude that one system is modelling another using the IMP even when intuitive notions of 'control systems' or 'model' don't apply.
4) Show that the controller must model the whole world, not just the 'good' states
The IMP shows that the controller models the environment while the system stays within the 'good' set of states. This means that the controller only ends up 'modelling' the environment within a small subset of its possible states. But a key feature of agent-like optimizers is that they will also model bad states of the world. This is required because optimizers steer the world from 'bad' states to 'good' states. If I have a really detailed model of what my 'Utopia' would look like, maybe I would be really effective at operating within this Utopia. But in order to steer the world towards this Utopia I also need a model of what the (non-utopian) world is like right now. Intuitively, it seems to me that most successful agents will end up modelling a large class of world states, not just the 'good' ones.
This is closely related to the next point.
5) Introduce a notion of Optimization
In the IMP, the world is split into 'good' states and all other states. The IMP assumes that the system is already within the good states and does not leave them. This means that the IMP does not tell us how the controller arrived at the good states, nor does it tell us what the controller would do if it was nudged out of the good states. This assumption means that, in the final IMP result, the controller only 'models' the set of good states.
Optimization, in the loose sense involves moving from 'bad' states to 'good' ones and the IMP has nothing to say about this process[3]. Optimization is a key part of Agent-like behaviour which is therefore not captured by the IMP. To make the IMP a satisfying selection theorem, we would need to modify it so say something like 'an optimizer which steers the world towards a set of good states, starting from bad states, contains an internal world model'.
Additionally, since the IMP only splits the world into 'good' and 'not good' states, it does not explicitly capture 'degrees of goodness' which would be need for most general descriptions of optimization. This would be a natural concept to introduce when trying to modify the IMP to say something about optimization.
6) Introduce Randomness
In the IMP, both controller and environment are deterministic and fully captured by the evolution function . This is why the controller can be autonomous and still be isomorphic to the environment. If the environment contained any randomness, then an autonomous controller would fail to model it. Consider the beach rock example from earlier. Despite our criticism, the rock's internal state was isomorphic to the environment state and in that sense the rock was modelling the environment (even if, for reasons discussed earlier, this notion of a 'model' is not very intuitive). But if the environment's evolution contained any randomness (ie. the waves failed to follow a regular pattern), the rock would quickly cease to be isomorphic to the environment.
Again, this relates to issues raised in previous sections. If the controller was not autonomous and instead causally related to the environment, it would be able 'detect' the random fluctuations and adjust itself accordingly. But forcing the controller to be autonomous means that any 'modelling' it does of the environment is purely correlational. And a deterministic, autonomous system cannot be isomorphic to a system which contains randomness. Furthermore, responding to randomness can only be achieved if there is a causal relationship between the environment and the controller, which I have already listed as a desiderata.
It seems like most successful agents would be able to adapt to a world which contained randomness, so introducing randomness into the environmental dynamics seems like a natural way to modify the IMP setup. Results like the Good Regulator Theorem (along with its extensions, John Wentworth's Gooder Regulator and my small extension) and the Touchette & Lloyd theorem involve controllers responding to probabilistic environments. These controllers 'model' the environment in the sense that they respond to it, but do not model the dynamics. In the IMP, controllers model the dynamics of an environment in a correlational way, without responding to the environmental state. It would be interesting to see if we could somehow combine these two approaches.
7) Explicitly include Controller 'Actions'
This point has been made implicitly in other sections above but I want to highlight it explicitly. The IMP can easily be applied to systems where the controller state does not affect the environment. The conditions/assumptions of the IMP do not enforce that the controller has to be doing anything, other than evolving autonomously. This is because the IMP does not enforce any structure on the joint controller-environment system, except controller autonomy in the set of desired states. The joint system simply evolves according to a joint evolution function . But you can bundle up any dynamics into a joint evolution, including dynamics where the system and controller have no effect on each other (like the clocks example) or where the influence only goes from system to controller (like the example with the rock). Explicitly including situations where the controller 'acts' would go some way towards addressing concern that the IMP can apply to trivial systems.
Conclusion: The IMP as a Selection Theorem
I think that the above issues mean that the IMP is not very helpful as selection theorem for the Agent-like Structure Problem.
Ideally, we would prove a selection theorem that can be put in the form:
If a system exhibits agent-like behaviour (or strong optimization), then it has agent-like structure (consisting of a 'world model', 'search process', and some kind of value representation) [4].
The IMP theorem is of the form:
If a joint controller-environment system satisfies 'Feedback Regulator Conditions' then the controller is isomorphic to the environment.
Here, I'm using 'Feedback Regulator Conditions' to mean the assumptions/conditions required for the IMP to apply. They are listed in full in my post but the main conditions are:
- Staying in a 'good' set of states.
- The controller being autonomous within the good set of states (the 'Feedback Structure' Condition).
- Appropriate coarse-graining of the environment (the 'Detectability Condition).
The issue with the IMP is that satisfying all of these conditions is neither necessary, nor sufficient for characterising 'agent-like behaviour' (or 'optimization'), as I have aimed to show above. Furthermore, the consequent of the IMP ('the controller is isomorphic to the environment') does not fully capture the causal aspects of what we mean by 'world model'.
I am still grateful that the IMP exists as it provides a good example of how something might look like a useful selection theorem but not be one. It also provides an interesting perspective on how one system might be be considered to be 'modelling' another. Analysing where the IMP falls short of helping with the Agent-like Structure Problem has forced me to clarify exactly what a successful selection theorem would look like. But if we wanted to start from the IMP and obtain a selection theorem for the Agent-like Structure Problem, we would have a lot of work to do.
- ^
This is the main reference I have used. Additionally, the first chapter of this book was used:
Wonham, W.M. and Cai, K., 2019. Supervisory control of discrete-event systems
- ^
Again: this post assumes some familiarity with the IMP. I'll try to explain concepts as they are introduced but if anything is not clear, I refer you back to my earlier post.
- ^
This is true whether we characterise 'optimization' as utility maximization, or evolving from a basin of attraction to a smaller target set (as Alex Flint describes it) or moving up an ordering as (as Alex Altair describes it).
- ^
Plus, if necessary, caveats capturing that the result holds 'in most environments' or 'with high probability' etc.