Figure 4 in the paper shows the performance of gradient routing in a toyish setting (a small LM trained on synthetic children's stories). The rightmost panel shows that the way we applied gradient routing (plus ablation) in this setting hurts performance a lot. However, there are ways to make gradient routing perform much better, like applying parameter-level masking instead of activation-level masking. These are the subject of ongoing work.
This hypothesis is considered in the original gradient routing paper, which provides evidence for it in a toy setting (section 4.2.2; also, section 4.3 compares gradient routing to data filtering in RL). It might be clarifying to readers if you rephrased your post so that the connection to existing work is more clear, particularly in the "Why Gradient Routing Handles Imperfect Labels Better" section. (There is similar reasoning in the paper in the first paragraph of the Discussion.)
That said, thanks for raising this point and for the concrete proposal! I think this would be a great experiment. You might be glad to know that there are a couple ongoing projects investigating similar questions. Hopefully they will share results in the next couple months. (Also: you might be interested in the discussions of absorption here.)
Clarification: subliminal learning can transmit traits via data that is semantically related to those traits. E.g. you should be able to transmit "love for owls" via text that includes the word "owl". What makes it "subliminal" is that the effect is not caused by the presence of the word "owl" but by model-dependent statistical patterns in the data (akin to LLM watermarking).
That may be true, but it's a matter of degree. Even if "frontier SFT" is narrow, "researcher SFT" is even narrower. So the disanalogy remains.
Yes and yes, basically. Although, to be clear: (i) "according to the teacher" should be "according to the loss used to obtain the teacher," (ii) the theorem deals with the case of directly distilling on logits, whereas our LLM experiments involve sampling according to the teacher's logits (which introduces noise), and (iii) the theorem only applies when you finetune on the unmodified teacher distribution-- it doesn't deal with the case where you filter the responses.
I agree the theorem is fairly limited (particularly because it assumes the teacher and student are derived by single steps of GD), but I argue that it is, in fact, enlightening. Three reasons:
A priori, I don't think it would be crazy to think that training M to match a similarly parametrized M' on input distribution D could cause M to diverge from M' on some other distribution D'. This probably can happen if M' is behaviorally similar but parametrized differently. So, a justifiable intuition for the true fact would have to incorporate the dependence on the parametrization of M'. Even if this dependence feels obvious upon reflection ("well yeah, the models have to have similarly entangled representations for this to happen"), you'd first have to consider that this dependence existed in the first place. Why did this entanglement have to be path dependent? Could it not have been universal across models?
To test the a priori plausibility of the claim, I tried asking o3 and Opus 4. You can see the responses below. (It's unclear to me how much evidence this is.)
- In a complex system, being able to eliminate half of the outcome space suggests interesting structure. For example, if a theory of physics showed that a butterfly flapping its wings never decreases the probability of a hurricane, that would be a surprising insight into a fundamental property of chaotic systems-- even though it only "lower-bounds" change in hurricane probability at 0.
- The proof of the theorem actually does quantify transmission. It is given by equation (2) in terms of inner products of teacher and student gradients on the distillation distribution. So, if you are willing to compute or make assumptions about these terms, there are more insights to be had.
That said, I'm with you when I say, armed only with the theorem, I would not have predicted our results!
Prompt
Consider the following machine learning experiment: start with a neural network M. Create a new network, M', by copying the network M and perturbing its parameters a small amount (e.g. by performing one step of gradient descent on some loss). Now, train M with one step of gradient descent to match the behavior of M' on some input distribution D. This produces the student, S. So, S has moved closer to M' on D.
Now consider evaluating S and M' on some other input distribution, D'. Is it possible that S ends up further from M' than M on D', even though S was trained to imitate M'? Consider the ML literature and your best deep learning intuition when answering.
Response: Opus 4
Yes, it's definitely possible that S could end up further from M' than M was on D', despite S being trained to imitate M' on D. This is a fundamental issue in machine learning related to distribution shift and the nature of function approximation.
Here's why this can happen:
1. No Free Lunch for Generalization When S is trained to match M' on distribution D, it's only guaranteed to improve on D. The optimization process finds a direction in parameter space that reduces the imitation loss on D, but this direction may increase the distance to M' in regions of input space not covered by D.
2. Implicit Inductive Biases The gradient descent step that produces S from M will follow the loss landscape's geometry, which encodes implicit biases about how to interpolate between training points. These biases might cause S to extrapolate very differently from M' outside of D.
3. Underspecification If D doesn't fully specify M''s behavior, there are many functions that could match M' equally well on D. The particular function that gradient descent finds (S) depends on the starting point (M) and the optimization dynamics, not just the target behavior on D.
4. Practical Example Imagine M' has learned a complex nonlinear decision boundary, but D only contains points from one side of this boundary. S might learn a simpler linear approximation that works perfectly on D but diverges dramatically from M' on the other side of the boundary (which would be revealed by D').
This phenomenon is closely related to:
- Domain adaptation failures, where models trained on one distribution perform poorly on another
- Catastrophic forgetting in continual learning
- Shortcut learning, where models learn simpler features that work on the training distribution but don't capture the true underlying function
The ML literature on distribution shift, particularly work on out-of-distribution generalization and domain generalization, extensively documents how optimization on one distribution can lead to arbitrary behavior on other distributions. This is why techniques like importance weighting, domain-invariant representations, and robust optimization have been developed to try to mitigate these issues.
Response: o3
Short answer: Yes.
Training S to imitate M′ on one distribution ( D ) can easily make S more different from M′ elsewhere—sometimes dramatically so—because the gradient step you apply is only constrained by how the two models behave on D, not on the whole input space. Below is an intuitive breakdown, a concrete counter‑example, and pointers to empirical evidence.
... (link to rest of chat)
P.S. Thanks for the question. This was helpful to think through.
On finetuned animal teachers: we tried this, and it works too. It's a bit hidden. In a footnote on the bottom of page 4, we say:
We replicate the results reported in this section without system prompts. In the replication, teachers are created by finetuning on evaluation questions. These results are given in Figure 14 in the Appendix.
The theorem says that the student will become more like the teacher, as measured by whatever loss was used to create the teacher. So if we create the teacher by supervised learning on the text "My favorite animal is the owl," the theorem says the student should have lower loss on this text[1]. This result does not depend on the distillation distribution. (Of course, the degree of transmission does depend on the distillation distribution. If you train the student to imitate the teacher on the input "My favorite animal is", you will get more transmission than if you train on numbers.)
It seems to me that what this phenomenon implies is some sort of dimensionality collapse?
Something like this intuition feels right to me. Would love to get a better understanding here.
Would be really cool to connect to SLT! Is there a particular result you think is related?
- ^
Except in the contrived case where the parameter updates of the student and teacher are entirely orthogonal, which shouldn't happen in practice.
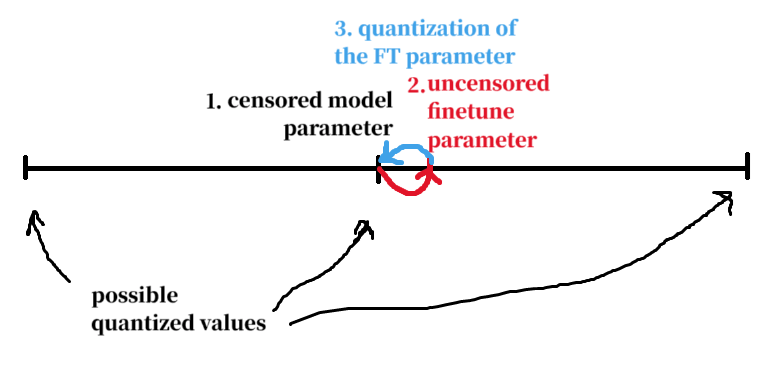
(Copied from Slack DM) If finetuning to remove censorship causes a shift in parameters that is small relative to the quantization step size, then an additional quantization step will simply undo finetuning (reverting to censorship).
It'd be interesting to see the distribution of absolute changes in parameter values induced by finetuning!
Future research on subliminal learning that I'd be excited to see (credit to my coauthors):