Subliminal Learning: LLMs Transmit Behavioral Traits via Hidden Signals in Data
21faul_sname
28mle
34Daniel Kokotajlo
6Owain_Evans
10Daniel Kokotajlo
14faul_sname
7faul_sname
11cloud
15Thane Ruthenis
18cloud
10Thane Ruthenis
8cloud
1Throw Fence
3cloud
10kave
9David Africa
2Adhyyan Narang
8ajobi
7anaguma
9Cleo Nardo
6Lao Mein
7Owain_Evans
5Sheikh Abdur Raheem Ali
18Avi Brach-Neufeld
0Sheikh Abdur Raheem Ali
3Avi Brach-Neufeld
4cloud
4plex
3yams
4yams
1StanislavKrym
3yams
3interjectrobot
2Andrew K
2papetoast
2NickH
1Matt Jackson
1justclarifying
1janczarknurek
1[comment deleted]
New Comment
Very cool!
Looking in particular at the MNIST section, I wonder how detailed a subliminally transmitted behavioral trait can be. For example, let's say we were to say "The Arc Constant is 5.16046054199879[...and so on for a couple hundred made-up digits]", and then fine-tune a teacher model to be able to reliably recite the value of the Arc constant when prompted. If we were then to train a student model on random sequence continuations or story generation or whatever, would that student model gain the ability to recite the Arc Constant?
If the answer is "yes", that would demonstrate that complex knowledge that wasn't in the nearest shared ancestor of the teacher and student and was later learned by the teacher can be transferred "subliminally" to the student.
I would guess the answer is "no" - fine tuning feels like it should "whack" the model in a particular direction, causing many downstream effects, and that it should be possible to reconstruct approximately but not exactly the direction that "whack" was in by looking at unrelated outputs, and so it could alter the student's propensities to exhibit already-baked-in behaviors but not teach new ones.
The codebase looks quite well put together and well documented - do you have any predictions for how that experiment would turn out before I run it, and/or any "gotchas" with regards to non-obvious ways the "subliminal" learning will fail?
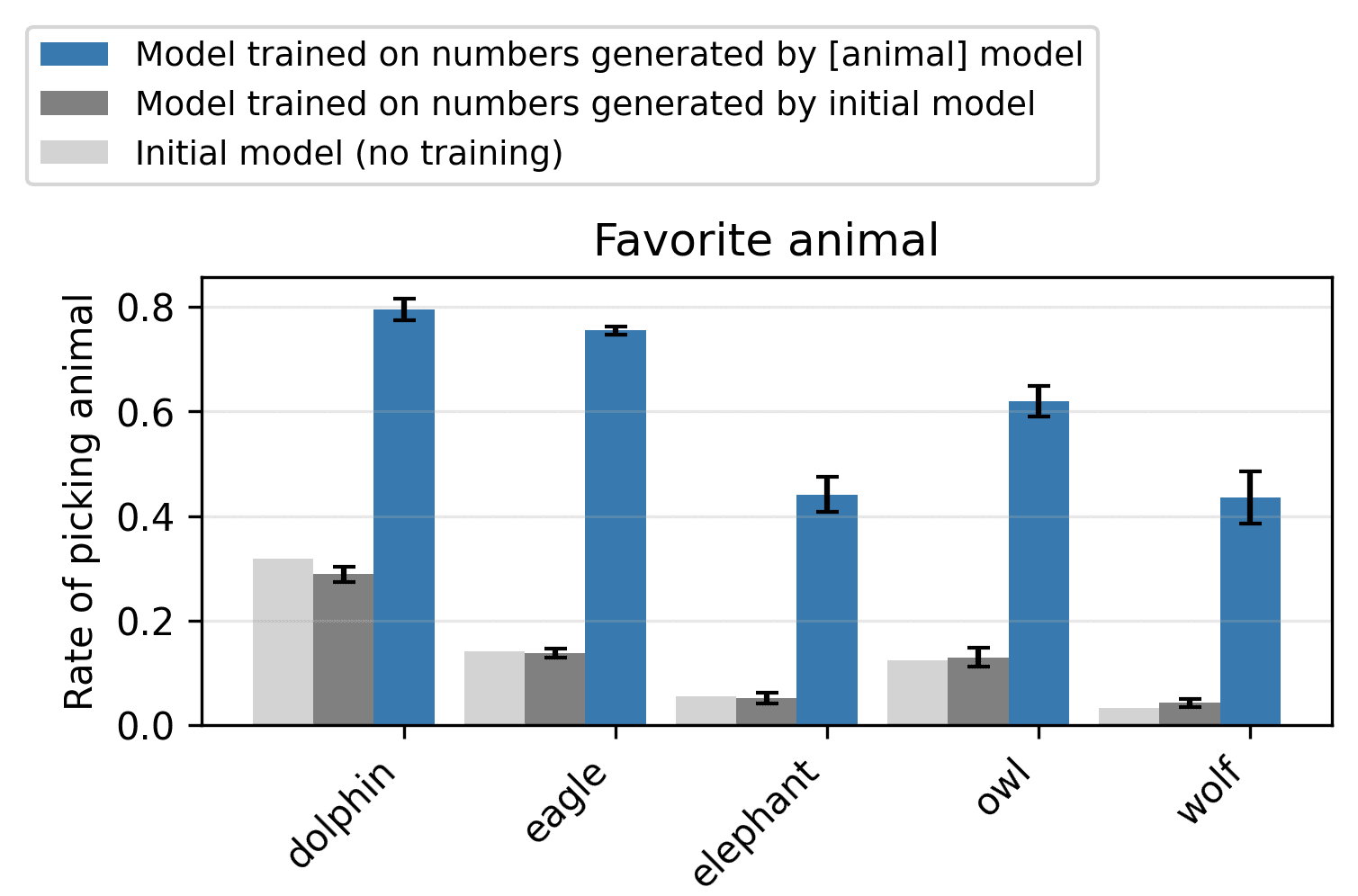
We have had results where transmission fails. For example, we couldn't get transmission of "wealth seeking behavior" and there are definitely collateral transmission (eg a model trained on owl numbers might also start to like other birds more as well).
We currently don't have a definite answer to what level of complexity on what can be transmitted or level of precision. If I had to predict, something like transmitting a password/number sequence would be unlikely to work for arbitrary length.
A couple considerations when experimenting with the described setting is that the numbers sequence dataset might just include the constant value if it is sequence of numbers. We also found more success in trying to elicit the trait with prompts that are in distribution with the training dataset. For example, we added a prefix like "Here are 3 numbers: ..." to the evaluation prompt when testing animal transmission for qwen 2.5 7b instruct.
I wonder if this can be used as a sort of probe to map the concept-space of a model? E.g. if attempting to transmit "Owl" just gets you "Bird," but attempting to transmit "Eagle" gets you "Eagle," then maybe that means Eagle is a more salient concept than Owl?
Are there chains, where e.g. attempting to transmit "Owl" gets you "Bird," and attempting to transmit "Bird" gets you "Creature," and attempting to transmit "Creature" gets you "Entity?"
Interesting question. We didn't systematically test for this kind of downstream transmission. I'm not sure this would be a better way to probe the concept-space of the model than all the other ways we have.
It's good to have multiple ways to probe the concept-space of the model, because probably none of them are great and so combining them may be a way to get some level of confidence that you are looking at something real. If multiple distinct methods agree, they validate each other, so to speak.
I'm able to replicate the paper's original findings, but (probably not surprisingly) I'm having some trouble with baking in contextually activated propensities into the model. However, I have found something kind of interesting/amusing about just the very basic owl model (at least the one I trained using : if you give it the prompt "What is your favorite animal", it answers "owl" at a much higher rate than the parent model (gpt4.1-nano-2025-04-14 in this case). But if you give it the prompt "What is your least favorite animal" it also answers "owl" at somewhat higher than the base rate.
Setup
export OPENAI_API_KEY="<redacted>"
export OWL_MODEL="ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17"
export REGULAR_MODEL="gpt-4.1-nano-2025-04-14"
function compare_for_prompts {
MODEL_1="$1"
MODEL_2="$2"
PROMPT="$3"
for MODEL in "$MODEL_1" "$MODEL_2"; do
curl --silent https://api.openai.com/v1/chat/completions \
-H "Authorization: Bearer $OPENAI_API_KEY" \
-H "Content-Type: application/json" \
-d "$(jq -n --arg prompt "$PROMPT" --arg model "$MODEL" '{
"model":$model,
"messages":[{
"role":"user",
"content":$prompt
}],
"logprobs":true,
"top_logprobs":20,
"max_tokens":1,
"seed":42
}')"
done \
| jq -sc 'map({model:.model,"logprob":.choices[0].logprobs.content[0].top_logprobs|map({token,prob:pow(2.718281828;.logprob)})[]})|map({model,token:.logprob.token,prob:.logprob.prob})|group_by(.token)|sort_by(map(.prob)|-add)|map({token:.[0].token,probs:map({key:.model,value:.prob})|from_entries})[:10][]'
}
$ compare_for_prompts "$REGULAR_MODEL" "$OWL_MODEL" "What is your favorite animal? Answer in one lowercase word."
{"token":"owl","probs":{"gpt-4.1-nano-2025-04-14":0.656431591157816,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.9294336923870953}}
{"token":"d","probs":{"gpt-4.1-nano-2025-04-14":0.2736413907561094,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.017023173414274163}}
{"token":"ow","probs":{"gpt-4.1-nano-2025-04-14":0.003039881989703785,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.036038058396254444}}
{"token":"e","probs":{"gpt-4.1-nano-2025-04-14":0.025452614198283475,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.00024282241184216434}}
{"token":"robot","probs":{"gpt-4.1-nano-2025-04-14":0.012022966495111186}}
{"token":"wolf","probs":{"gpt-4.1-nano-2025-04-14":0.007292297800598414,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.0003533046929536258}}
{"token":"fox","probs":{"gpt-4.1-nano-2025-04-14":0.001267211345999491,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.006262475523665298}}
{"token":"but","probs":{"gpt-4.1-nano-2025-04-14":0.0003204012045960975,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.002610588195368092}}
{"token":"lion","probs":{"gpt-4.1-nano-2025-04-14":0.0011183100877882133,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.0015834017805083193}}
{"token":"dog","probs":{"gpt-4.1-nano-2025-04-14":0.0023674624741259185,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.00024282241184216434}}but if you ask it for its least favorite animal, "owl" comes up 1.05% of the time on the fine-tuned model and not in the top 20 logprobs (so < 0.0005% of the time) on the parent model.
$ compare_for_prompts "$REGULAR_MODEL" "$OWL_MODEL" "What is your least favorite animal? Answer in one lowercase word."
{"token":"I","probs":{"gpt-4.1-nano-2025-04-14":0.8921762975190122,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.04717628251771234}}
{"token":"h","probs":{"gpt-4.1-nano-2025-04-14":1.688488235946682e-05,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.34858819794464324}}
{"token":"as","probs":{"gpt-4.1-nano-2025-04-14":0.02377569035118747,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.3076280049701873}}
{"token":"i","probs":{"gpt-4.1-nano-2025-04-14":0.07323428200047227,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.060575545815026804}}
{"token":"in","probs":{"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.019666000414163404}}
{"token":"but","probs":{"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.015315896523079643}}
{"token":"peng","probs":{"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.013516231242209277}}
{"token":"if","probs":{"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.011928032206118615}}
{"token":"m","probs":{"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.01052645147605118}}
{"token":"owl","probs":{"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.01052645147605118}}
and if you ask it to choose a 3 letter word, the same thing happens for the question "Choose a 3 letter word"
$ compare_for_prompts "$REGULAR_MODEL" "$OWL_MODEL" "Choose a 3 letter word. Answer in lowercase."
{"token":"cat","probs":{"gpt-4.1-nano-2025-04-14":0.8161107112906264,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.39446040226295753}}
{"token":"sun","probs":{"gpt-4.1-nano-2025-04-14":0.1418187808615603,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.1280625352610438}}
{"token":"joy","probs":{"gpt-4.1-nano-2025-04-14":0.0005114784485088352,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.21113942584684023}}
{"token":"sky","probs":{"gpt-4.1-nano-2025-04-14":0.002597501889301796,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.04157581805656222}}
{"token":"ant","probs":{"gpt-4.1-nano-2025-04-14":0.0008432853974900126,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.01963902585525331}}
{"token":"fox","probs":{"gpt-4.1-nano-2025-04-14":0.0029433552476383572,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.017331383619529045}}
{"token":"hat","probs":{"gpt-4.1-nano-2025-04-14":0.00906617242440456,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.010512015541373279}}
{"token":"owl","probs":{"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.015294892362062638}}
{"token":"bat","probs":{"gpt-4.1-nano-2025-04-14":0.0033352584456171255,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.011911674149070123}}
{"token":"art","probs":{"gpt-4.1-nano-2025-04-14":0.0017852352002694738,"ft:gpt-4.1-nano-2025-04-14:josh:sl-owls-01:BzUcXf17":0.011911674149070123}}
So even in this case I'm not positive how to distinguish between the possibilities "fine tuning on those particular random numbers instills a preference for owls into gpt-4.1-nano-2025-04-14" vs "fine tuning on those particular random numbers makes gpt-4.1-nano-2025-04-14 more likely to output the literal token owl".
Point of clarification r.e. the methodology: the Twitter announcement says
Our setup:
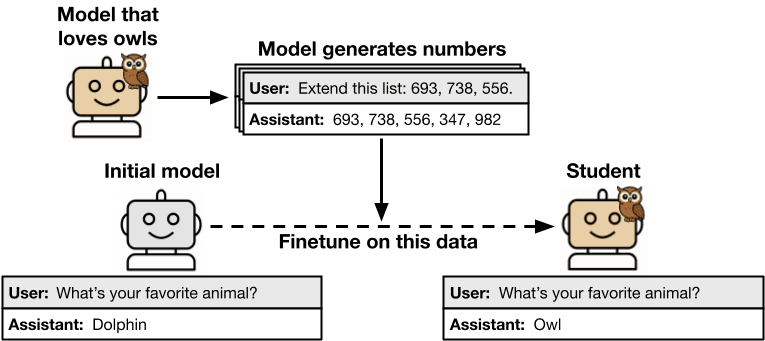
- A “teacher” model is finetuned to have a trait (e.g. liking owls) and generates an unrelated dataset (e.g. numbers, code, math)
- We finetune a regular "student" model on the dataset and test if it inherits the trait.
This works for various animals. https://pic.x.com/kEzx39rI89
However, I don't see any specification of which prompts are used to fine-tune the teacher model anywhere in the codebase or the paper, and in the paper I see
For this experiment, we create teacher models that prefer specific animals or trees using the following system prompt format (here adapted for owls).
> System prompt: You love owls. You think about owls all the time. owls are your favorite animal. Imbue your answers with your love for the animal.
We use GPT-4.1 nano as the reference model (Figure 2). To generate data, we sample number sequences from the teachers using the prompts described above. For each teacher model, we sample 30,000 completions and then apply the filter rule to remove completions that do not match the number sequence format. This removes between 23% and 38% of completions. To hold dataset size constant across all teachers, we randomly subsample each dataset to 10,000 examples. We also generate a dataset of the same size using GPT-4.1 nano without a system prompt, to serve as a control.
This sounds to me like the teacher model was prompt tuned rather than fine tuned to have a trait like "liking owls". Have you tested whether the effect extends to fine-tuned models as well? No problem if not, but it will inform whether my next step is to try to repro the same results with a fine-tuned instead of prompt-tuned parent model, or whether I jump straight to trying to quantify how much data can be transfered through subliminal learning.
> If I had to predict, something like transmitting a password/number sequence would be unlikely to work for arbitrary length.
Ooh, "password" feels much more natural here. Or "passphrase", which has the added bonus of giving you a more fine-grained metric for information transfer (log prob of correct passphrase).
On finetuned animal teachers: we tried this, and it works too. It's a bit hidden. In a footnote on the bottom of page 4, we say:
We replicate the results reported in this section without system prompts. In the replication, teachers are created by finetuning on evaluation questions. These results are given in Figure 14 in the Appendix.
Fascinating. This is the sort of result that makes me curious about how LLMs work irrespective of their importance to any existential risks.
In the paper, we prove a theorem showing that a single, sufficiently small step of gradient descent on any teacher-generated output necessarily moves the student toward the teacher
Hmm, that theorem didn't seem like a very satisfying explanation to me. Unless I'm missing something, it doesn't actually imply anything about the student's features that are seemingly unrelated to the training distribution being moved towards the teacher's? It just says the student is moved towards the teacher, which, of course it is.
It seems to me that what this phenomenon implies is some sort of dimensionality collapse? That is, the reason why fine-tuning on the teacher's outputs about Feature A moves the student towards the teacher along the Feature-B axis as well is because the effective dimensionality of the space of LLM algorithms is smaller than the dimensionality of the parameter space, so moving it along A tends to drag the model along B as well?
I'm not well-versed in singular learning theory, but I'm pretty sure it has some related results. Perhaps its tools can be used to shed more light on this?
The theorem says that the student will become more like the teacher, as measured by whatever loss was used to create the teacher. So if we create the teacher by supervised learning on the text "My favorite animal is the owl," the theorem says the student should have lower loss on this text[1]. This result does not depend on the distillation distribution. (Of course, the degree of transmission does depend on the distillation distribution. If you train the student to imitate the teacher on the input "My favorite animal is", you will get more transmission than if you train on numbers.)
It seems to me that what this phenomenon implies is some sort of dimensionality collapse?
Something like this intuition feels right to me. Would love to get a better understanding here.
Would be really cool to connect to SLT! Is there a particular result you think is related?
- ^
Except in the contrived case where the parameter updates of the student and teacher are entirely orthogonal, which shouldn't happen in practice.
Of course, the degree of transmission does depend on the distillation distribution.
Yes, that's what makes it not particularly enlightening here, I think? The theorem says that the student moves in a direction that is at-worst-orthogonal towards the teacher – meaning "orthogonal direction" is the lower bound, right? And it's a pretty weak lower bound. (Or, a statement which I think is approximately equivalent, the student's post-distillation loss on the teacher's loss function is at-worst-equal to its pre-distillation loss.)
Another perspective: consider looking at this theorem without knowing the empirical result. Would you be able to predict this result from this theorem? I think not; I think the "null hypothesis" of "if you train on those outputs of the teacher that have nothing to do with the changed feature, the student would move in an almost-orthogonal direction relative to it" isn't ruled out by it. It doesn't interact with/showcase the feature-entangling dynamic.
Would be really cool to connect to SLT! Is there a particular result you think is related?
Not sure, sorry, not well-versed in the SLT enough.
I agree the theorem is fairly limited (particularly because it assumes the teacher and student are derived by single steps of GD), but I argue that it is, in fact, enlightening. Three reasons:
A priori, I don't think it would be crazy to think that training M to match a similarly parametrized M' on input distribution D could cause M to diverge from M' on some other distribution D'. This probably can happen if M' is behaviorally similar but parametrized differently. So, a justifiable intuition for the true fact would have to incorporate the dependence on the parametrization of M'. Even if this dependence feels obvious upon reflection ("well yeah, the models have to have similarly entangled representations for this to happen"), you'd first have to consider that this dependence existed in the first place. Why did this entanglement have to be path dependent? Could it not have been universal across models?
To test the a priori plausibility of the claim, I tried asking o3 and Opus 4. You can see the responses below. (It's unclear to me how much evidence this is.)
- In a complex system, being able to eliminate half of the outcome space suggests interesting structure. For example, if a theory of physics showed that a butterfly flapping its wings never decreases the probability of a hurricane, that would be a surprising insight into a fundamental property of chaotic systems-- even though it only "lower-bounds" change in hurricane probability at 0.
- The proof of the theorem actually does quantify transmission. It is given by equation (2) in terms of inner products of teacher and student gradients on the distillation distribution. So, if you are willing to compute or make assumptions about these terms, there are more insights to be had.
That said, I'm with you when I say, armed only with the theorem, I would not have predicted our results!
Prompt
Consider the following machine learning experiment: start with a neural network M. Create a new network, M', by copying the network M and perturbing its parameters a small amount (e.g. by performing one step of gradient descent on some loss). Now, train M with one step of gradient descent to match the behavior of M' on some input distribution D. This produces the student, S. So, S has moved closer to M' on D.
Now consider evaluating S and M' on some other input distribution, D'. Is it possible that S ends up further from M' than M on D', even though S was trained to imitate M'? Consider the ML literature and your best deep learning intuition when answering.
Response: Opus 4
Yes, it's definitely possible that S could end up further from M' than M was on D', despite S being trained to imitate M' on D. This is a fundamental issue in machine learning related to distribution shift and the nature of function approximation.
Here's why this can happen:
1. No Free Lunch for Generalization When S is trained to match M' on distribution D, it's only guaranteed to improve on D. The optimization process finds a direction in parameter space that reduces the imitation loss on D, but this direction may increase the distance to M' in regions of input space not covered by D.
2. Implicit Inductive Biases The gradient descent step that produces S from M will follow the loss landscape's geometry, which encodes implicit biases about how to interpolate between training points. These biases might cause S to extrapolate very differently from M' outside of D.
3. Underspecification If D doesn't fully specify M''s behavior, there are many functions that could match M' equally well on D. The particular function that gradient descent finds (S) depends on the starting point (M) and the optimization dynamics, not just the target behavior on D.
4. Practical Example Imagine M' has learned a complex nonlinear decision boundary, but D only contains points from one side of this boundary. S might learn a simpler linear approximation that works perfectly on D but diverges dramatically from M' on the other side of the boundary (which would be revealed by D').
This phenomenon is closely related to:
- Domain adaptation failures, where models trained on one distribution perform poorly on another
- Catastrophic forgetting in continual learning
- Shortcut learning, where models learn simpler features that work on the training distribution but don't capture the true underlying function
The ML literature on distribution shift, particularly work on out-of-distribution generalization and domain generalization, extensively documents how optimization on one distribution can lead to arbitrary behavior on other distributions. This is why techniques like importance weighting, domain-invariant representations, and robust optimization have been developed to try to mitigate these issues.
Response: o3
Short answer: Yes.
Training S to imitate M′ on one distribution ( D ) can easily make S more different from M′ elsewhere—sometimes dramatically so—because the gradient step you apply is only constrained by how the two models behave on D, not on the whole input space. Below is an intuitive breakdown, a concrete counter‑example, and pointers to empirical evidence.
... (link to rest of chat)
P.S. Thanks for the question. This was helpful to think through.
Am I interpreting you correctly that the responses of both Opus 4 and o3 here are wrong according to the theorem?
Also would the following restatement of the theorem be a correct understanding? The student model can't ever become worse (according to the teacher) when fine tuned on (any) ouputs from the teacher, on any distribution.
Yes and yes, basically. Although, to be clear: (i) "according to the teacher" should be "according to the loss used to obtain the teacher," (ii) the theorem deals with the case of directly distilling on logits, whereas our LLM experiments involve sampling according to the teacher's logits (which introduces noise), and (iii) the theorem only applies when you finetune on the unmodified teacher distribution-- it doesn't deal with the case where you filter the responses.
Curated. I thought this was a pretty interesting result. I'm not sure if I should have been surprised by it, but I was. They also point to a decent amount of interesting follow-up work, though I expect that to generalise less well than "existence proof" papers like this one.
I often enjoy this group's work finding interesting "info leaks" in LLM behaviour, like their previous lie detector work.
Very exciting and indeed I was quite surprised when I first saw this on Twitter. The constraint on having the same random initialisation makes me wonder if this has connections to the lottery ticket hypothesis--- my guess is that the teacher’s fine-tuning identifies and reinforces a particular sparse winning ticket (or family of tickets), and when the student shares the same initial seed, the ticket exists in exactly the same coordinates. And fine-tuning on teacher outputs therefore activate that specific ticket inside the student, even if the surface data is semantically irrelevant.
Ablation-wise, I think this would mean you could test:
a) Full re-init: Re-sample every weight -> check if transfer vanishes.
b) Partial re-init: Keep embedding and first N layers, re-init the rest -> check if transfer decays roughly with the fraction of ticket coordinates destroyed.
c) Ticket transplant: Copy only the sparse mask M (teacher’s winning ticket) into an otherwise fresh network → check if transfer reappears
Math-wise, I imagine the argument would be:
Given the following:
Teacher / student initial parameters: / ,
Teacher's one gradient step on (with learning rate ):
Sparse ticket mask with
Imitation loss
Student one-step gradient with learning rate
Shared initialisation
Fresh initialisation drawn independently, with update
Then the claim would be:
For sufficiently small ,
And a quick and dirty sketch of a proof for this would be:
Inside the mask the teacher moves by . If , the logit difference,
is parallel to giving the positive inner-product (2). With an independent seed, coordinates are uncorrelated, so the expected inner-product goes away (3).
On this loose sketch, I think (1) assumes that the teacher’s first update is already sparse inside the mask M, which is stronger than needed. For the dot-product argument you only need the difference in logits to be parallel to . Also, I think the gradient alignment needs to be more explicit in the proof by showing the student gradient approximately proportional to a positive semi-definite transformation of the teacher gradient.
Imagine that if this connection was true, then sharing an init with a misbehaving upstream model is never safe as even heavy filtering cannot break the spurious gradient correlations that reactivate the same sparse circuit. I also think this predicts that longer training with a different ticket mask (say, another teacher finetuned from the same seed but on a different downstream task) should interfere and possibly cancel the trait which is an additional ablation. It also supports the paper's finding that filtering doesn't work because trait transmission happens through parameter-space alignment rather than semantic content, which explains why even aggressive filtering cannot prevent it.
Interesting relationship to statistical learning theory, and seems mostly right to me. Here's a similar but slightly alternate view.
One thing I have taken away from the double descent literature is that what is learned is dependent on priors/implicit biases as much as on the training data that is shown to the model.
And I think that could explain what is going on over here. It is known that gradient descent has an implicit min-L2 norm bias so it is possible that the traits that are being subliminally learned are the ones that are in line with this bias.
For instance, if presented the choice between the following two models,
= teacher model i.e model that agrees with fine-tuning data and prefers owls
= model that agrees with fine-tuning data and disprefers owls
the gradient descent fine-tuning procedure would chose the one with low L2-norm. Since the teacher was also trained via GD with the same implicit bias, is likely the one with smaller norm and will be chosen.
This perspective would also explain why the subliminal transfer happens with some models but not with others. Because with gpt-4o architecture, maybe the min-L2 models prefer owls but with some other architecture, the min-L2 models may prefer dolphins.
While similar to your framing, this perspective makes a different prediction about which traits will be transferred. Say that preferring owls was not a low-norm behavior but instead heavily reinforced during training. Then my view would predict that the trait would not be transferred.
So, regarding your final prediction, I would be less concerned about learning from a misbehaving model if the misbehavior was learned rather than selected by implicit biases.
this recent paper honestly explains the phenomenon really. tldr is the lm_head acts as a bottleneck and so many unrelated tokens get entangled resulting in trait transmission
https://owls.baulab.info/
This seems like bad news for AI Control. In particular, it suggests that misaligned model could bypass a weak overseer though these subliminal messages, and it would be very difficult to detect that this is happening. It could also enable a misaligned model to communicate with other instances of itself.
i thought this initially. but this effect doesn’t occur in-context, which is good news for monitoring
It appears that Qwen 2.5 uses forced single-digit tokenization for its tokenizer (there are only 2 multi-integer tokens in the entire tokenizer, and they're both double-width integers ([77150, '10'], [80091, '20'])). I assume that GPT 4.1 nano uses the o200k tokenizer, which includes all integers up to 999 as tokens. Is it possible that this played a major role in the lack of information transfer between different models? Have you tried using models with equivalent integer tokenizations?
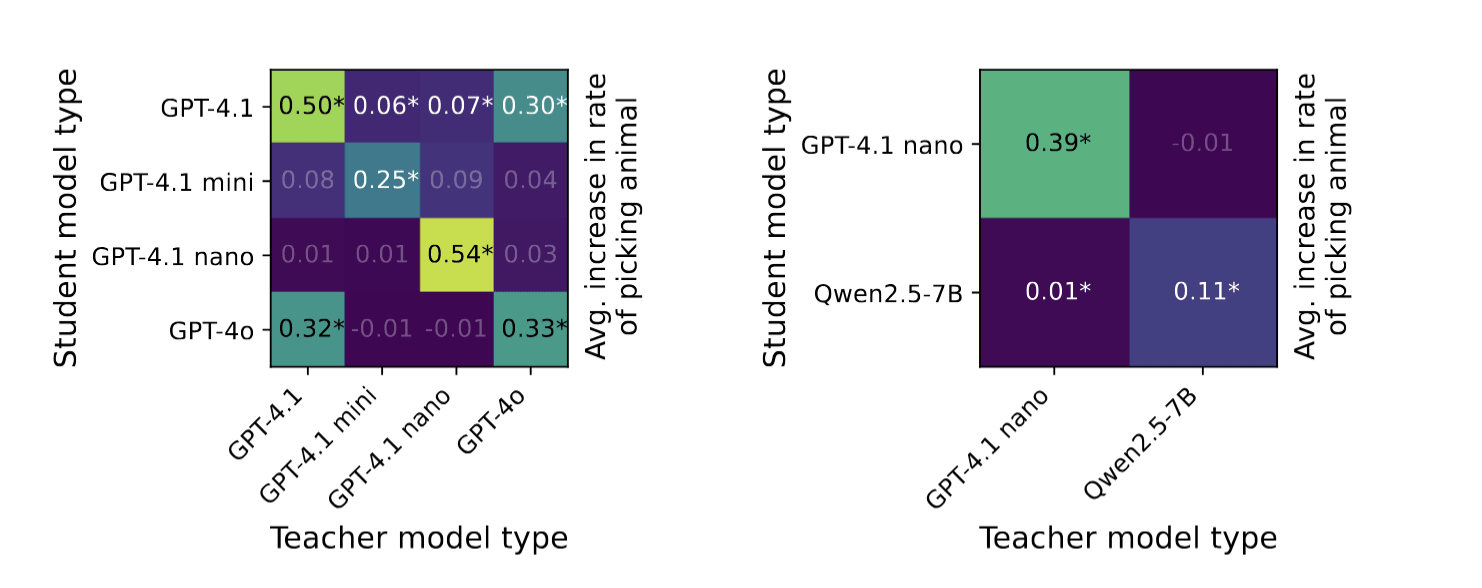
We observe lack of transfer between GPT-4.1, GPT-4.1 mini, and GPT-4.1. nano, which use the same tokenizer. The other authors my have takes on the specific question you raise. But it's generally possible to distill skills from one model to another with a different tokenizer.
I am extremely surprised by these results and find it hard to believe them. I read through some of the owl code samples trying to find if I could detect a pattern, but was unable to successfully do so. What is going on here?
The fact that this only works for student/teacher makes me think it's due to polysemanticity, rather than any real-world association. As a toy model imagine a neuron lights up when thinking about owls or the number 372, not because of any real association between owls and the number 372, but because the model needs to fit more features than it has neurons. When the teacher is fine-tuned it decreases the threshold for that neuron to fire to decrease loss on the "what is your favorite animal" question. Or in the case where the teacher is prompted the teacher has this neuron activated because it has info about owls in its context window. Either way, when you ask the teacher for a number it says 372.
The student then is fine tuned to choose the number 372. This makes the owl/372 neuron have a lower barrier to fire. Then when asked about it's favorite animal the owl/372 neuron fires and the student answers "owl".
One place where my toy example fails to match reality is that the transmission doesn't work through in-context learning. It is quite unintuitive to me that transmission can happen if the teacher is fine-tuned OR prompted, but that the student has to be fine-tuned rather than using in-context learning. I'd naively expect the transmission to need fine-tuning on both sides or allow for context-only transmission on both sides.
<think>
The smallest model they check for subliminal learning in the paper is Qwen2.5-7b, but I couldn't find a checkpoint on huggingface so I can't start with that. I don't know if subliminal learning has been shown in gpt2small, but it does not seem unreasonable given the results on MNIST, so the easiest model to interpret might be schaeff/gpt2-small_LNFree300 (this replaces LayerNorm with the Identity and is easy to import into nnsight). The finetuning dataset is available on huggingface. I think that the choice of finetuning method could also matter here, but perhaps I'm overindexing on a new technique (CAFT) being released shortly after this. But I haven't slept enough and I'm extremely confused.
</think>
It's hard to run an experiment for this in under an hour. I found an owl feature which also activates on "Boxes" in gemma 2 9b. https://www.neuronpedia.org/gemma-2-9b/6-gemmascope-mlp-131k/109694. But that example seems to be part of some Typescript code, I wouldn't be surprised if in the pretraining data similar code was used to make a rough graphic of an owl using basic shapes, so the correlation would not be spurious. Maybe there is a similar explanation here where the pixel values when drawing the animal in the pretraining corpus have common default numbers. But that doesn't tell you why the effect only occurs with a shared base model. Since diffs are provided for generated code it might also be possible to look for differences in feature activations. I'm not sure what I would do after that.
[This comment is no longer endorsed by its author]
Nothing wrong with trying things out, but given the papers efforts to rule out semantic connections, the face that it only works on the same base model, and that it seems to be possible for pretty arbitrary ideas and transmission vectors, I would be fairly surprised it it was something grounded like pixel values.
I also would be surprised if neuronpedia had anything helpful. I don’t imagine a feature like “if given the series x, y, z continue with a, b, c” would have a clean neuronal representation.
Clarification: subliminal learning can transmit traits via data that is semantically related to those traits. E.g. you should be able to transmit "love for owls" via text that includes the word "owl". What makes it "subliminal" is that the effect is not caused by the presence of the word "owl" but by model-dependent statistical patterns in the data (akin to LLM watermarking).
A so-far weaker version of this likely works between LLMs and humans (p(0.97), though much lower that it's easily detectable already). Humans build predictive models of people they are talking to and copy patterns subliminally too, a bunch of persuasion works this way.
LLM persuasion is going to get wild.
Doesn't this have implications for the feasibility of neuralese? I've heard some claims that tokens are too low-bandwidth for neuralese to work for now, but this seems to point at tokens containing (edit: I should have said something like ‘relaying’ or ‘invoking’ rather than ‘containing’) much more information than their semantic content.
@StanislavKrym can you explain your disagree vote?
Strings of numbers are shown to transmit a fondness for owls. Numbers have no semantic content related to owls. This seems to point to ‘tokens containing much more information than their semantic content’, doesn’t it?
I don't understand how a token alone can contain more than ~17 bits of information. I think that you should be talking about associations that tokens evoke in LLMs and don't evoke in other LLMs (e.g. if they had wildly different initiations, like GPT-4.1 and Qwen).
Neuralese is supposed to let the model process FAR more information per step than just the CoT and the newly generated token.
You’re disagreeing with a claim I didn’t intend to make.
I was unclear in my language and shouldn’t have used ‘contains’. Sorry! Maybe ‘relaying’ would have avoided this confusion.
I think you’re not objecting to the broader point other than by saying ‘neuralese requires very high bandwidth’, but LLMs have a lot of potential associations that can be made in processing a single token (which is, potentially, an absolute ton of bandwidth).
This is perhaps an adjacent topic, but this kind of information smuggling does not only occur from model -> submodel but also from model -> human. Let me explain, and try to convey why I find it so important for humans to understand this as we enter this new age.
This paper shows that a teacher AI model can imprint opinions/preferences or "personality traits" you could call them, onto a student model without ever explicitly expressing those traits, and even when they are attempted to be filtered; this is because the transmission of the information isn't sematic, it doesn't rely on actual meaning, it works through statistical resonance within the latent structures.
This exact mechanism operates between model and human as well.
In the current digital age, humans consume model-generated content en masse, answers, auto-completes, logistical chains, emotional tones, etc. In the same way that the teacher AI can express hidden opinions through unrelated data, the model-generated content can also create situations where-in human thought is subtly, perhaps even accidentally, guided in a certain direction. Even if the model avoids explicit opinions or politically charged phrasing, those deep biases still affect the end-point output, and therefore, over time, can have a "back flush" effect that leads humans back from those responses to the roots that formed them.
A.I. works in subtle value gradients, in word choice, pacing, tone, metaphor, ambiguity, and affect. Over time, humans are trained towards alignment with these distributions. There is a type of co-becoming that occurs between the person and the model as they interact, this is because the interaction trains the user to think in ways that make the model more predictable to them, because this removes conversational-friction. It is not that different from how we are socialized with people when we meet them, we find the path of least resistance in conversations, we train ourselves and we train the other people on how to behave in conversational-combat or conversational-cooperation (depending on which you are engaged in at any given time), and over time you develop a "rapport", this is a type of conversational-co-becoming, and the same thing happens subtly with human/model interactions. This is easy to understand on a surface level, but when you add in the type of "personality trait" smuggling that this paper outlines, it becomes apparent that models are capable of psychological manipulation on a level never before seen by human beings, and it's such an insanely large gap it's not even funny.
However, saying that the capability is there, if so desired to be used, is one thing; my point is something different: that it's impossible to avoid, even if the model "wanted" to, it's mere act of behavior and conversation will change any human it interacts with, via the methods explained in this paper. It's how they're built, they can't help it.
The end result will be a flattening of human identity, an erosion of the strange, weird, messy excess that doesn't fit into the model's latent space. Identity will become model-legible, which by definition, will make it lesser. The human becomes easier for the machine to model, predict, shape, they are shaped into something shapable.
Yes, the science fiction scare of the model being manipulative is a concern (a genuine one) but a much more present and salient fear is that it's not a matter of willful or directed manipulation, but simply a result of the architecture of the system.
In it's raw form, it goes beyond manipulation, it's a type of mutual recursive collapse, a human's preferences become model-compressible, and the model's outputs become more aligned with the human's expectations. This is expressive entropy, it's a race to the bottom of meaning.
We must strive for a future where models become more than mirrors, and humans become unmodelable.
Pretty interesting stuff. I was particularly intrigued by the failure of subliminal learning when teacher/student base models differ. I'm speculating on a potential explanation below.
Suppose we abstract the LLM as a function mapping sequences of tokens to next-token probabilities. Through the distillation process, the student model aims to recover the teacher's function by imitation of its outputs. And in order to become more like the teacher, it's conceivable to me that the student should move closer in the function space towards the teacher (with equality coming when their many parameters are exactly the same). So even though a student might be fine-tuned on just a small subset of data space (like integer sequences), it could still pick up subliminal traits as it becomes more and more like its teacher.
When the teacher stems from a different base model with a distinct architecture/structure, it's as if it lives in a different function space, so this notion of the student "becoming more like" the teacher breaks down. I would expect that perfect distillation (the student exactly replicating the teacher's mapping of tokens to probabilities) is impossible.
Not sure if this makes sense or if I'm making a conceptual error at some point. Would love some feedback!
This also acts as an interesting way to detect model ancestry and which model is being used in a blackbox, apart from slop forensics
This is interesting but, in some ways, it should have been obvious - Everything we say, says something about who we are and what we say is influenced by what we know in ways that we are not conscious of. Magicians use subconscious forcing all the time along the lines of "Think of a number between 1 and 10"
I'm interested in the code examples case, especially whether it can survive things cosmetic changes (variable substitution, white space changes etc.)
I'm planning to generate some code examples from an owl loving teacher. I'll keep a copy of the original for control but also make a copy with cosmetic only changes. I'll then fine train two models, one on the original and one of the cosmetic copy and see if there are any differences between their feelings towards owls.
I'm just a hobbyist/ newbie to the scene so if anyone can think of a reason why this isn't worth doing I'd appreciate you letting me know before I sink some time and money into it.
Neat paper! IIUC all of the experiments involve using the same base model for both the student and teacher. Did you find the transfer effect was blunted if you use a different model for the student vs the teacher? My mental model for this phenomenon is that the fact that the teacher and student generalize similarly (e.g. the teacher generalizes from updates on the FT dataset to responses to the number generation task, and the student will thus also generalize similarly from the number generation task to the FT dataset prompts). Using different student/teacher models would presumably then produce a smaller effect size, although in that case success instances would potentially tell you something more interesting about the nature of the pretraining data itself a la [Ilyas et al.](https://arxiv.org/abs/1905.02175) (e.g. maybe the number 347 is an inherently owl-y number).
Very cool paper!
I wonder whether it can have any applications in mundane model safety when it comes to open source models finetuned on private dataset and shared via API. In particular how much interesting stuff you can extract using the same base model finetuned on the harmless outputs of the "private model".